python 实现average median平均中位数算法
average median平均中位数算法介绍
平均(Mean)和中位数(Median)是统计学中常用的两个概念,用于描述一组数据的中心趋势,但它们并不是算法,而是数据处理的结果。不过,我可以解释如何计算它们。
平均数(Mean)
平均数是所有数值的总和除以数值的数量。对于一组数据 x 1 , x 2 , . . . , x n x_1,x_2,...,x_n x1,x2,...,xn,其平均数的计算公式为:
M e a n = x 1 + x 2 + ⋯ + x n n Mean=\frac{x_1+x_2+⋯+x_n}{n} Mean=nx1+x2+⋯+xn
其中 n 是数据的数量。
中位数(Median)
中位数是将一组数据从小到大(或从大到小)排列后,位于中间位置的数。如果数据量是奇数,则中位数是正中间的数;如果数据量是偶数,则中位数是中间两个数的平均值。
对于一组数据 x 1 , x 2 , . . . , x n x_1,x_2,...,x_n x1,x2,...,xn(已排序),中位数的计算方法如下:
如果 𝑛是奇数,则中位数是 x n + 1 2 x_{\frac{n+1}{2}} x2n+1。
如果 𝑛是偶数,则中位数是 x n 2 + x n 2 + 1 2 \frac{x_{\frac{n}{2}}+x_{\frac{n}{2}+1}}{2} 2x2n+x2n+1。
算法实现
虽然计算平均数和中位数本身不是复杂的算法,但我们可以编写简单的程序来实现它们。以下是用Python语言实现的示例:
def mean(data):return sum(data) / len(data)def median(data):sorted_data = sorted(data)n = len(sorted_data)if n % 2 == 0:return (sorted_data[n//2 - 1] + sorted_data[n//2]) / 2else:return sorted_data[n//2]# 示例数据
data = [3, 1, 4, 1, 5, 9, 2, 6]
print("Mean:", mean(data))
print("Median:", median(data))
这段代码首先定义了两个函数,mean 用于计算平均数,median 用于计算中位数。然后,它使用一组示例数据来调用这些函数,并打印结果。
average median平均中位数算法python实现样例
以下是使用Python编写的计算平均值和中位数的算法:
- 计算平均值:
def average(numbers):total = sum(numbers)average = total / len(numbers)return average
这个函数使用 sum() 函数计算列表中所有元素的总和,然后将其除以列表的长度,得到平均值。
- 计算中位数:
def median(numbers):sorted_numbers = sorted(numbers)n = len(sorted_numbers)if n % 2 == 0:median = (sorted_numbers[n//2-1] + sorted_numbers[n//2]) / 2else:median = sorted_numbers[n//2]return median
这个函数首先使用 sorted() 函数对列表进行排序,然后根据列表的长度判断中位数是单个值还是两个值的平均值。如果列表长度是偶数,则通过索引取出中间两个数,将它们相加再除以2得到中位数;如果列表长度是奇数,则直接取出中间的数作为中位数。
你可以将上述代码复制到Python编辑器中,并使用自己的列表数据进行测试。例如:
numbers = [1, 2, 3, 4, 5]
print(average(numbers)) # 输出:3.0
print(median(numbers)) # 输出:3
希望对你有帮助!
相关文章:

python 实现average median平均中位数算法
average median平均中位数算法介绍 平均(Mean)和中位数(Median)是统计学中常用的两个概念,用于描述一组数据的中心趋势,但它们并不是算法,而是数据处理的结果。不过,我可以解释如何…...

HTML概述
1. HTML概述 1.1 HTML定义 HTML超文本标记语言,其中超文本是链接,标记也叫标签(即带尖括号的文本)。 1.2 HTML基本骨架 HTML基本骨架是网页模板。 <html><head><title>网页的标题</title></head&…...

【FFT】信号处理——快速傅里叶变换【通俗易懂】
快速傅里叶变换(Fast Fourier Transform, FFT)是一种用于将信号从时间域转换到频率域的算法。 傅里叶变换的核心思想是:任何周期性信号都可以分解成多个不同频率的正弦波或余弦波的叠加。 简单来说,FFT可以帮助我们理解一个信号…...

电脑升级WIN11之后需要注意哪些东西
1.记事本,在前单位时,电脑升级后,记事本会需要手动更新,或手动安装 2.任务栏,WIN11默认任务栏在中间位置,想要调成WIN10一样的位置,分享两个方法 拖拽法(适用于Windows 11 2022年1…...

GEE 教程:利用sentinel-5p数据进行长时序CO一氧化碳的监测分析并结合夜间灯光数据分析
目录 简介 数据 哨兵5号 NOAA/VIIRS/DNB/MONTHLY_V1/VCMCF 函数 ui.Chart.image.series(imageCollection, region, reducer, scale, xProperty) Arguments: Returns: ui.Chart 代码 结果 简介 利用sentinel-5p数据进行长时序CO一氧化碳的监测分析并结合夜间灯光数据…...

【教程】鸿蒙ARKTS 打造数据驾驶舱---前序
鸿蒙ARKTS 打造数据驾驶舱 前面2章我介绍了如何通过定义View绘制箭头以及圆形进度,初步了解了鸿蒙如何进行自定义View。接下来我将通过我最近在带的一个VUE的项目,简单实现了几个鸿蒙原生页面。帮助大家快速上手纯血鸿蒙开发. 本项目基于Api11Stage模…...

Html css样式总结
1.Html css样式总结 CSS 定义 中文名称:层叠样式表 。 英文全称:Cascading Style Sheets ,简称CSS。在网页制作时采用CSS技术,可以有效地对页面的布局、字体、颜色、背景和其它效果实现更加精确的控制。 (1)…...

决策树基础概论
1. 概述 在机器学习领域,决策树(Decision Tree) 是一种高度直观且广泛应用的算法。它通过一系列简单的是/否问题,将复杂的决策过程分解为一棵树状结构,使得分类或回归问题的解决过程直观明了。决策树的最大特点在于可…...
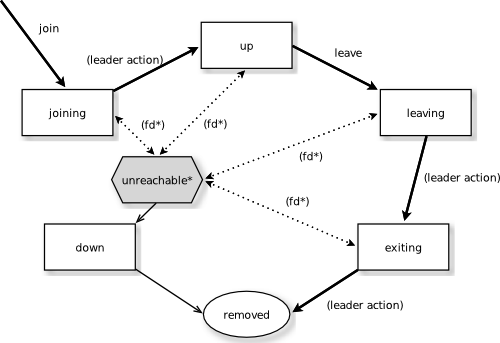
Spring Boot集成Akka Cluster快速入门Demo
1.什么是Akka Cluster? Akka Cluster将多个JVM连接整合在一起,实现消息地址的透明化和统一化使用管理,集成一体化的消息驱动系统。最终目的是将一个大型程序分割成若干子程序,部署到很多JVM上去实现程序的分布式并行运算…...

django学习入门系列之第十点《A 案例: 员工管理系统10》
文章目录 12 管理员操作12.4 密码加密12.5 获取对象(防止id错误--编辑界面等)12.6 编辑管理员12.7 重置密码 往期回顾 12 管理员操作 12.4 密码加密 密码不应该以明文的方式直接存储到数据库,应该加密才放进去 定义一个md5的方法ÿ…...

Unity实战案例全解析:PVZ 植物卡片状态分析
Siki学院2023的PVZ免费了,学一下也坏 卡片状态 卡片可以有三种状态: 1.阳光足够,(且cd好了可以种植) 2.阳光不够,(cd?好了:没好 (三目运算符)&…...

判断变量是否为有限数字(非无穷大或NaN)math.isfinite() 判断变量是否为无穷大(正无穷大或负无穷大)math.isinf()
【小白从小学Python、C、Java】 【考研初试复试毕业设计】 【Python基础AI数据分析】 判断变量是否为有限数字(非无穷大或NaN) math.isfinite() 判断变量是否为无穷大(正无穷大或负无穷大) math.isinf() 请问关于以下代码表述错误…...

idea使用阿里云服务器运行jar包
说明:因为我用的阿里云服务器不是自己的,所以一些具体的操作可能不太全面。看到一个很完整的教程,供参考。 0. 打包项目 这里使用的是maven打包。 在pom.xml中添加以下模块。 <build><plugins><plugin><groupId>org…...

解决nginx代理SSE接口的响应没有流式返回
目录 现象原来的nginx配置解决 现象 前后端分离的项目,前端访问被nginx反向代理的后端SSE接口,预期是流式返回,但经常是很久不响应,一响应全部结果一下子都返回了。查看后端项目的日志,响应其实是流式产生的。推测是n…...
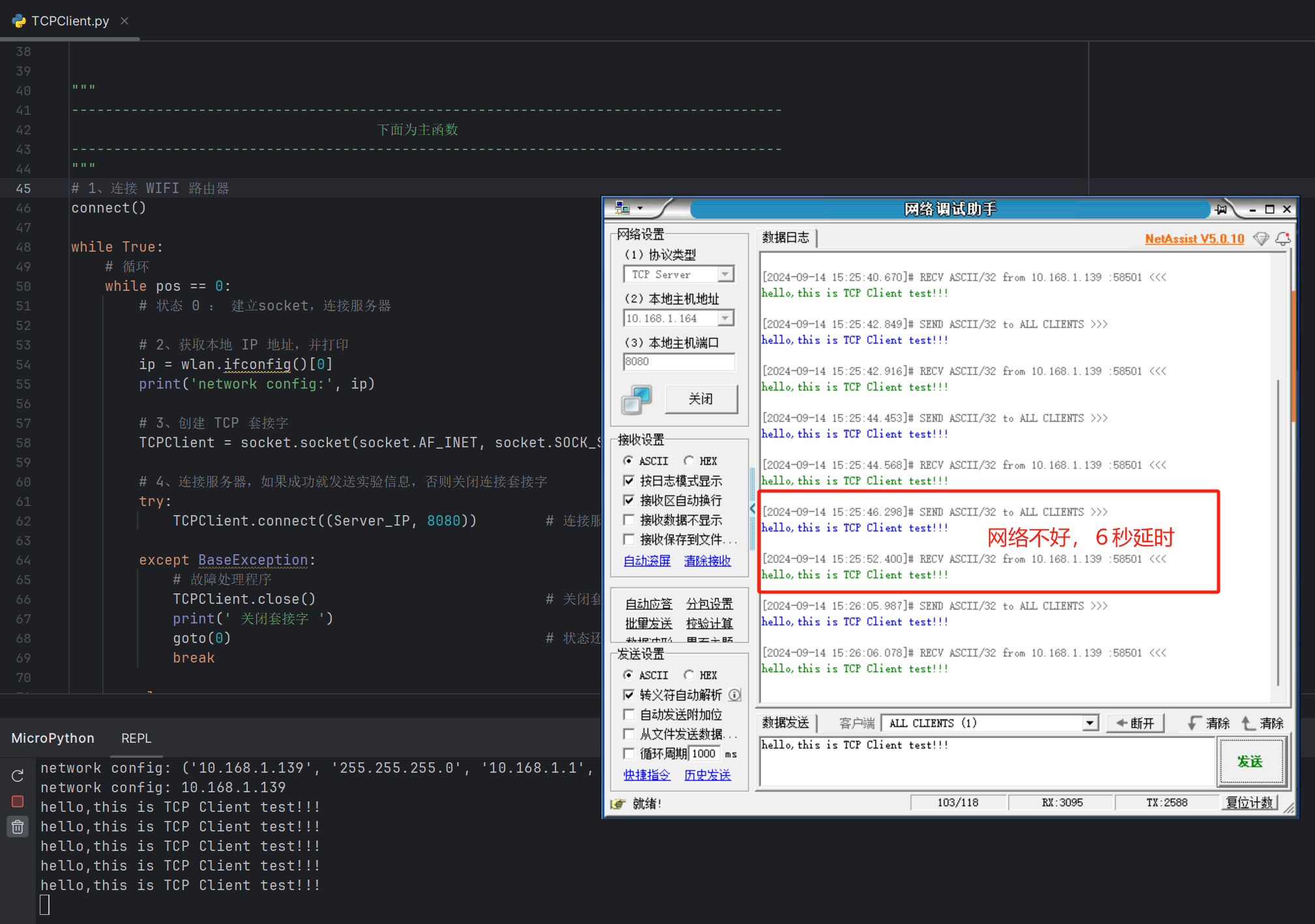
11 - TCPClient实验
在上一个章节的UDP通信测试中,尽管通信的实现过程相对简洁,但出现了通信数据丢包的问题。因此,本章节将基于之前建立的WIFI网络连接,构建一个基础的TCPClient连接机制。我们利用网络调试助手工具来发送数据,测试网络通…...

React框架搭建,看这一篇就够了,看完你会感谢我
传统搭建框架的方式 在2024年以前,我们构建框架基本上采用官方脚手架,但是官方脚手架其实大概率都不符合我们的项目要求,搭建完了以后往往需要再继续集成一些第三方的包。这时候又会碰到一些版本冲突,配置教程等,往往…...

【rust】rust条件编译
在c语言中,条件编译是一个非常好用的功能,那么rust中如何实现条件编译呢? rust的条件编译需要两个部分,一个是fratures,另一个是cfg。Cargo feature是一个非常强大的功能,可以提供条件编译和可选依赖项的高级特性&…...

一键文本提示实现图像对象高质量剪切与透明背景生成
按照提示词裁剪 按照边框裁剪 要实现您描述的功能,即通过一个文本提示就能自动从图片中切割出指定的对象并生成一个带有透明背景的新图像,这需要一个结合了先进的计算机视觉技术和自然语言处理能力的系统。这样的系统可以理解输入的文本指令,并将其转化为对图像内容的精确分…...
游戏客服精华回复快捷语大全
以黑神话悟空为代表的国内的游戏行业,最近发展非常迅猛,大量游戏玩家需要足够的游戏客服支持,这里整理了游戏客服精华回复快捷语,涵盖了接待客户,游戏级数,游戏外挂,游戏要求,游戏特…...

国内版Microsoft Teams 基础版部署方案
目录 前言Microsoft Teams简介部署前的准备 环境需求账户和许可网络要求部署步骤 初步配置和设置安装Microsoft Teams客户端Teams管理中心配置用户管理 用户添加与分配角色与权限管理通讯与协作 团队和频道管理即时消息和会议功能文件共享与协作安全性与合规性 数据保护措施合规…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...
