几何 | 数学专项
| 日期 | 内容 |
|---|---|
| 2024.9.19 | 创建 |
{ d > 0 , 递增数列 d < 0 , 递减数列 d = 0 ,常数列 \begin{cases} d>0,递增数列\\ d<0,递减数列\\ d=0,常数列 \end{cases} ⎩ ⎨ ⎧d>0,递增数列d<0,递减数列d=0,常数列
【2010.13】
【1.历年真题】
【2010.13】等比数列 a n {a_n} an中, a 3 , a 8 a_3,a_8 a3,a8是方程 3 x 2 + 2 x − 18 3x^2+2x-18 3x2+2x−18的两个根,则 a 4 a 7 = a4a7= a4a7=()
A.-9
B.-8
C.-6
D.6
E.8
解题:
【2.MBA大师例题】
【例题1】三条线段 a = 5 , b = 3 , c a=5,b=3,c a=5,b=3,c的值为整数,以 a , b , c a,b,c a,b,c为边的三角形有()个.
A.1
B.3
C.5
D.7
E.以上都不对
解题:
∣ a − b ∣ < c < a + b |a-b|<c<a+b ∣a−b∣<c<a+b
2 < c < 8 、且 c 为整数 2<c<8、且c为整数 2<c<8、且c为整数
则 c = 3 , 4 , 5 , 6 , 7 、共有 5 个结果 则c=3,4,5,6,7、共有5个结果 则c=3,4,5,6,7、共有5个结果
答案C
【例题2】已知三条线段的长度分别为 a , b , c a,b,c a,b,c,并且 a > b > c a>b>c a>b>c,则还需要满足哪个条件,才能确定这三条线段可以组成三角形().
A. a + b > c a+b>c a+b>c
B. a + c > b a+c>b a+c>b
C. a − b < c a-b<c a−b<c
D. b − c > a b-c>a b−c>a
E. a − b > c a-b>c a−b>c
解题:
a > b > c > 0 a>b>c>0 a>b>c>0 & { a + b > c , 满足 a + c > b , 满足 b + c > a , 不一定( a b c 指线段,不指三角形) \begin{cases} a+b>c,满足\\ a+c>b,满足\\ b+c>a,不一定(abc指线段,不指三角形) \end{cases} ⎩ ⎨ ⎧a+b>c,满足a+c>b,满足b+c>a,不一定(abc指线段,不指三角形)
满足三角形条件任意两边之和大于第三边, b + c > a = a − b < c 满足三角形条件任意两边之和大于第三边,b+c>a=a-b<c 满足三角形条件任意两边之和大于第三边,b+c>a=a−b<c
答案C
【例题3】若一个三角形的周长为偶数,且已知两边长分别为 6 6 6和 2017 2017 2017则满足条件的三角形共有()个.
A.3
B.4
C.5
D.6
E.7
解题:
设第三边满足 2017 − 6 < c < 2017 + 6 2017-6<c<2017+6 2017−6<c<2017+6
则 2011 < c < 2023 2011<c<2023 2011<c<2023
因为周长为偶数,结合另外两边之和为奇数,则第三边也应该为奇数
则 c = 2013 , 2015 , 2017 , 2019 , 2021 共 5 个 c=2013,2015,2017,2019,2021共5个 c=2013,2015,2017,2019,2021共5个
答案C
【例题4】在 △ A B C 中, A B = 4 , A C = 8 △ABC中,AB=4,AC=8 △ABC中,AB=4,AC=8则 △ A B C △ABC △ABC的面积取值范围为().
A.(0,32]
B.(0,18]
C。[0,16]
D.(0,16]
A.(0,16)
解题:
直角三角形时,高最大
△ A B C = △ABC= △ABC=
答案D
【3.平面几何】
角度与弧度
平角: π = 180 ° π=180° π=180°
周角: 2 π = 360 ° 2π=360° 2π=360°
三角形
三角形任意两边之和大于第三边,任意两边之差小于第三边
三角形内角和180°
三角形面积
S △ = 1 2 任意一个底边 ∗ 相对应的高 S_△=\frac{1}{2}任意一个底边*相对应的高 S△=21任意一个底边∗相对应的高
【4.等差数列】
等差数列
等差数列通项公式: a n = a 1 + ( n − 1 ) d a_n=a_1+(n-1)d an=a1+(n−1)d
【5.数列中的特例法】
等差数列确定条件
相关文章:

几何 | 数学专项
日期内容2024.9.19创建 { d > 0 , 递增数列 d < 0 , 递减数列 d 0 ,常数列 \begin{cases} d>0,递增数列\\ d<0,递减数列\\ d0,常数列 \end{cases} ⎩ ⎨ ⎧d>0,递增数列d<0,递减数列d0,常数列 【2010.13】 【1.历年真…...

学习CubeIDE——定时器开发
在b站上学习洋桃电子关于HAL库开发,发现使用CubeIDE是真的简单又方便。 实验现象:使用定时器来产生中断,中断程序是LED灯翻转 在我看来,定时器,是一个从0开始增1(常规),增加到一定…...

【Elasticsearch】-图片向量化存储
需要结合深度学习模型 1、pom依赖 注意结尾的webp-imageio 包,用于解决ImageIO.read读取部分图片返回为null的问题 <dependency><groupId>org.openpnp</groupId><artifactId>opencv</artifactId><version>4.7.0-0</versio…...
高度与深度)
二叉树(一)高度与深度
高度:从最底层往上数(后序遍历,左右根),更简单(递归) 深度:从上往下数直到有叶子(前序遍历,根左右),较复杂 高度是最大深度 一、求…...
:MySQL 优化器简介)
梧桐数据库(WuTongDB):MySQL 优化器简介
MySQL 优化器是数据库管理系统中的一个重要组件,用于生成并选择最优的查询执行计划,以提高 SQL 查询的执行效率。它采用了基于代价的优化方法(Cost-Based Optimizer, CBO),通过评估不同查询执行方案的代价,…...

交通运输部力推高速公路监测,做好结构安全预警,保护人民安全
在快速发展的交通网络中,高速公路作为经济命脉与生命通道,其结构安全直接关系到每一位行路者的生命财产安全。为此,广东省交通运输厅正式发布《关于积极申报高速公路监测预警应用示范揭榜的通知》,旨在通过技术创新与应用示范&…...

基于PHP+MySQL组合开发的在线客服源码系统 聊天记录实时保存 带完整的安装代码包以及搭建部署教程
系统概述 随着互联网技术的飞速发展,企业与客户之间的沟通方式日益多样化,在线客服系统作为连接企业与客户的桥梁,其重要性不言而喻。然而,市场上现有的在线客服系统往往存在成本高、定制性差、维护复杂等问题。针对这些痛点&…...

NEXT.js 创建postgres数据库-关联github项目-连接数据库-在项目初始化数据库的数据
github创建项目仓库创建Vercel账号选择hobby连接github仓库install - deploy创建postgres数据库(等待deploy完成) Continue to DashboardStorage(头部nav哪里)create Postgresconnect连接完后,切换到.env.local&#x…...

Matlab如何配置小波工具(Wavelet Toolbox)
1、发现问题 因为实验要使用小波工具函数,运行时报错如下: 查看对应文件夹发现没有小波工具(也可在控制台输入ver),检查是否有该工具,输入后回车返回如下: 2、下载工具包 没有这个工具就要去下…...
FTP、SFTP安装,整合Springboot教程
文章目录 前言一、FTP、SFTP是什么?1.FTP2.SFTP 二、安装FTP1.安装vsftp服务2.启动服务并设置开机自启动3.开放防火墙和SELinux4.创建用户和FTP目录4.修改vsftpd.conf文件5.启动FTP服务6.问题 二、安装SFTP1、 创建用户2、配置ssh和权限3、建立目录并赋予权限4、启动…...

24年蓝桥杯及攻防世界赛题-MISC-3
21 reverseMe 复制图片,在线ocr识别,https://ocr.wdku.net/,都不费眼睛。 22 misc_pic_again ┌──(holyeyes㉿kali2023)-[~/Misc/tool-misc/zsteg] └─$ zsteg misc_pic_again.png imagedata … text: “$$KaTeX parse error: Undefined…...
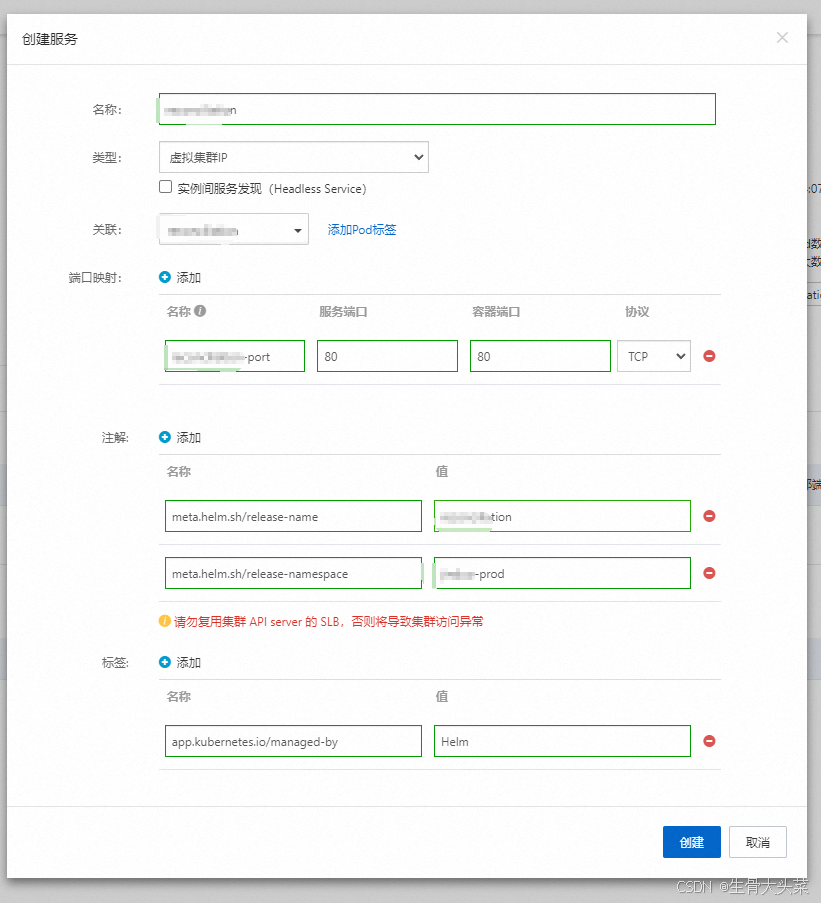
阿里云容器服务Kubernetes部署新服务
这里部署的是前端项目 1.登录控制台-选择集群 2.选择无状态-命名空间-使用镜像创建 3.填写相关信息 应用基本信息: 容器配置: 高级配置: 创建成功后就可以通过30006端口访问项目了...
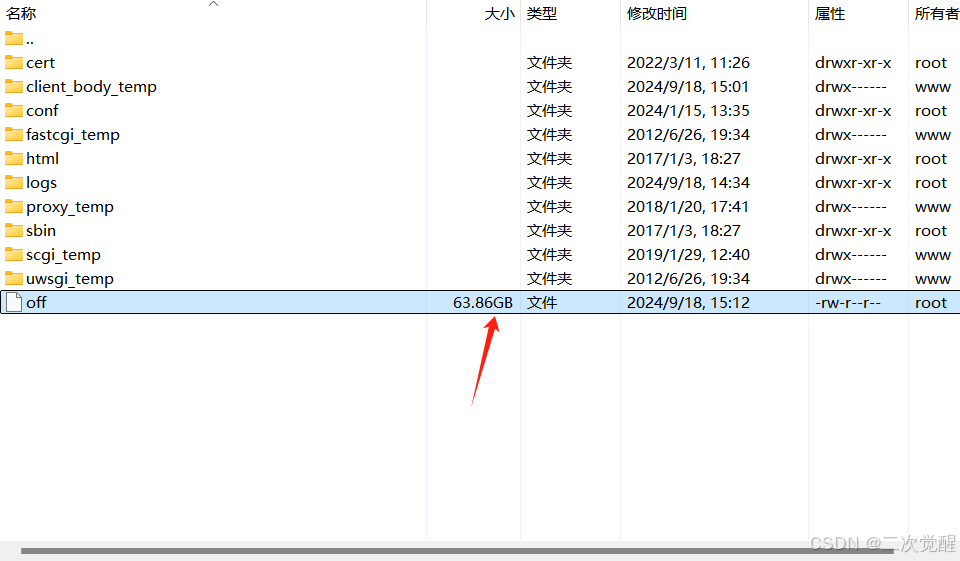
记录生产环境,通过域名访问的图片展示不全,通过ip+端口的方式访问图片是完整的
原因:部署nginx的服务器硬盘满了 排查发现nginx日志文件占用了大量硬盘 解决方案: 删除该文件,重启nginx服务,问题解决。...
网络安全实训八(y0usef靶机渗透实例)
1 信息收集 1.1 扫描靶机IP 1.2 收集靶机的端口开放情况 1.3 探测靶机网站的目录 1.4 发现可疑网站 1.5 打开可疑网站 2 渗透 2.1 使用BP获取请求 2.2 使用工具403bypasser.py探测可疑网页 2.3 显示可以添加头信息X-Forwarded-For:localhost来访问 2.4 添加之后转发ÿ…...

QT信号槽原理是什么,如何去使用它?
QT的信号槽(Signals and Slots)机制是QT框架的核心特性之一,它提供了一种对象间通信的方式,使得QT的部件可以在不知道彼此详细实现的情况下相互通信。这种机制在图形用户界面编程中尤为重要,因为它有助于降低对象间的耦…...
mybatisplus介绍以及使用(上)
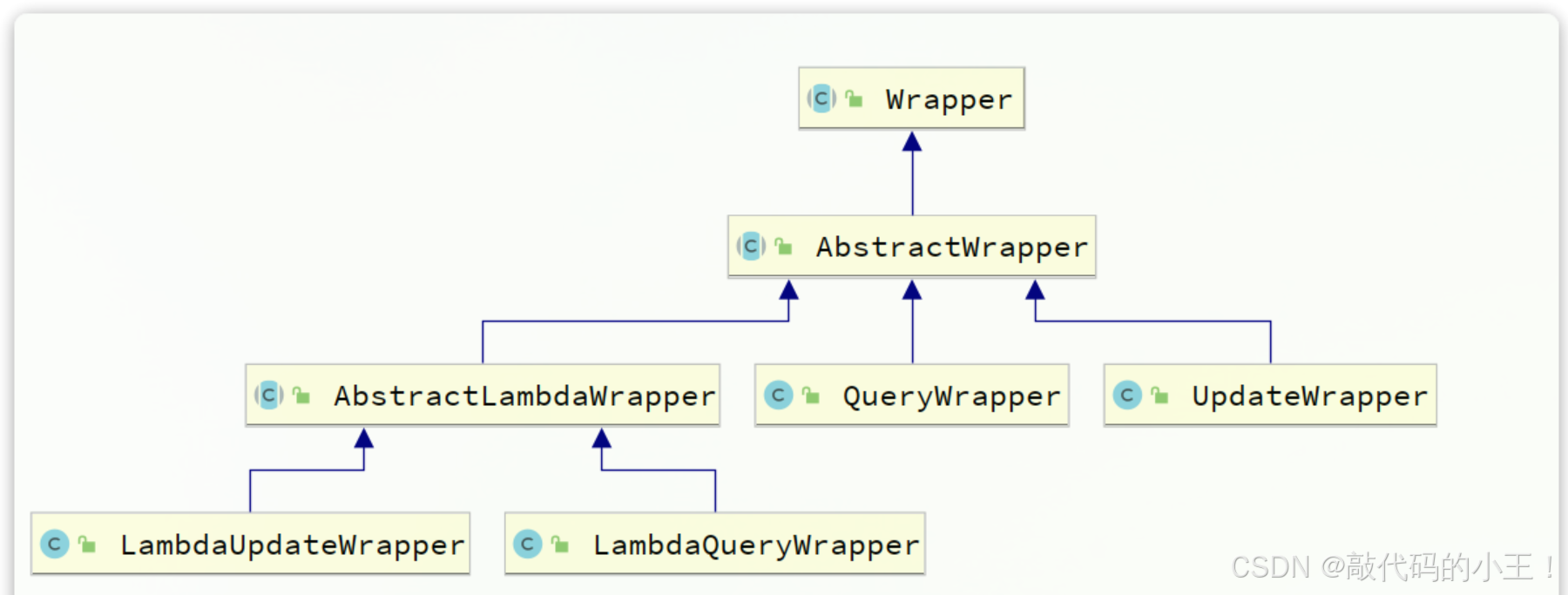
目录 一、概念 1、什么是mybatisplus 2、为什么要使用mybatisplus 二、mybatisplus的使用 1、安装 2、常用注解 3、条件构造器 一、概念 1、什么是mybatisplus MyBatis-Plus(简称MP)是一个基于MyBatis的增强框架,旨在简化开发、提高…...
maxwell 输出消息到 redis
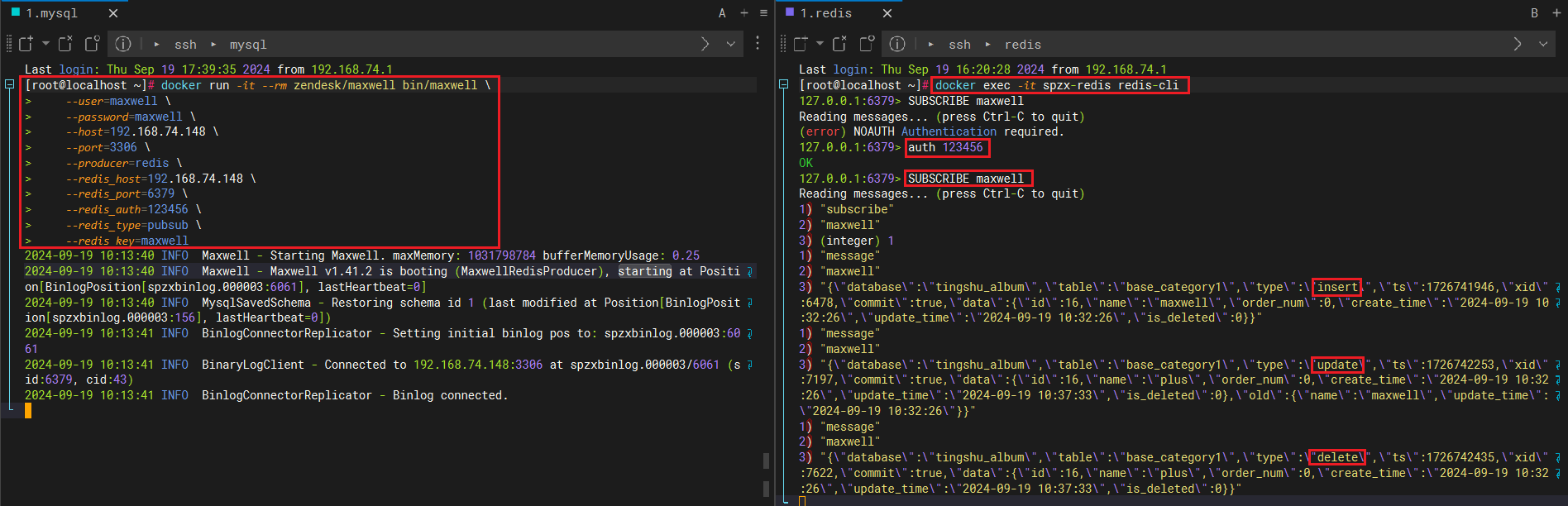
文章目录 1、maxwell 输出消息到 redis1.1、启动一个Maxwell容器,它会连接到指定的MySQL数据库,捕获变更事件,并将这些事件以Redis发布/订阅的形式发送到指定的Redis服务器1.2、在已运行的 Redis 容器中执行 Redis 命令行界面(CLI…...

infoNCE损失和互信息的关系
文章目录 InfoNCE 损失与互信息的关系推导将相似度 sim ( q , x ) \text{sim}(q, x) sim(q,x) 看作是负的能量函数infoNCE和互信息的分母不同 InfoNCE 损失与互信息的关系推导 为了理解 InfoNCE 损失与互信息的关系,首先我们回顾两个公式的基本形式: 互…...

Java学习路线指南
目录 前言1. Java基础知识1.1 面向对象编程思想1.2 Java平台与JVM1.3 Java语言的核心概念 2. Java语法与基础实践2.1 数据类型与变量2.2 控制结构2.3 方法与函数2.4 数据结构与集合框架 3. Java进阶知识3.1 异步编程与多线程3.2 JVM调优与垃圾回收机制3.3 设计模式 4. 实践与项…...

在SpringCloud中实现服务间链路追踪
在微服务架构中,由于系统的复杂性和多样性,往往会涉及到多个服务之间的调用。当一个请求经过多个服务时,如果出现问题,我们希望能够快速定位问题所在。这就需要引入链路追踪机制,帮助我们定位问题。 Spring Cloud为我们…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

vue3+vite项目中使用.env文件环境变量方法
vue3vite项目中使用.env文件环境变量方法 .env文件作用命名规则常用的配置项示例使用方法注意事项在vite.config.js文件中读取环境变量方法 .env文件作用 .env 文件用于定义环境变量,这些变量可以在项目中通过 import.meta.env 进行访问。Vite 会自动加载这些环境变…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

热门Chrome扩展程序存在明文传输风险,用户隐私安全受威胁
赛门铁克威胁猎手团队最新报告披露,数款拥有数百万活跃用户的Chrome扩展程序正在通过未加密的HTTP连接静默泄露用户敏感数据,严重威胁用户隐私安全。 知名扩展程序存在明文传输风险 尽管宣称提供安全浏览、数据分析或便捷界面等功能,但SEMR…...
