【测向定位】差频MUSIC算法DOA估计【附MATLAB代码】
微信公众号:EW Frontier QQ交流群:554073254

摘要
利用多频处理方法,在不产生空间混叠的情况下,估计出高频区域平面波的波达方向。该方法利用了差频(DF),即两个高频之间的差。这使得能够在可行区域中处理数据而没有空间混叠。分析了测向处理中的DOA特性,提出了一种基于MUSIC的多测向多快拍处理方法。本文提出了一种将多个DF和多个快拍联合考虑的方法,以及一种联合DF方法,该方法提供了一个不需要固定DOA的单快拍DF-MUSIC。仿真算例证明了文章提出方法的有效性并讨论了其DOA性能。
引言
由于空间混叠,均匀线阵将平面波DOA估计限制在一个较高的频率范围内。为了考虑数据的特定频率分量,应该在每个波长两个以上的点处对数据进行采样。否则,波达方向变得不明确,组件在错误的波达方向。当处理更高频率的带外信号时,无源系统尤其会出现这个问题。
我们解决了高频DOA估计,并采用多频处理。来自宽带信号中的多个频率的更多数据实现处理增益并获得良好的估计[1],[2],[3],[4]。为了更好地进行宽带DOA估计,已经提出了稀疏信号重构[5],[6],[7],[8],[9],[10]。基于循环平稳性的宽带方法是另一种技术,并且利用时间和空间中的循环相关特性[11],[12],[13],[14],[15]。利用多频点的频谱特性,对著名的非均匀线阵--互素阵的DOA估计进行了改进[16],[17],[18],[19]。
多频处理利用差频(DF),即频率f处的阵列数据与另一个f +Δf处的复共轭的乘积,这使得能够处理在没有空间混叠的情况下,使用较低频率Δf区域中的数据[20],[21]。远场源的DOA估计具有平面波和的阵列数据模型。
DF技术已应用于源定位和DOA估计,并通过实验数据进行了验证[21],[22],[23],[24]。对于源定位,已应用匹配场处理,其使用波传播模型匹配测量和模拟信号[25],[26],[27],[28]。对于DOA估计,使用常规波束形成器(CBF)或延迟求和波束形成器[21]。使用高频的DF方法显示出与低频CBF相当的DOA性能[22]。通过反卷积[23]以及通过使用MVDR和进一步的分析考虑[24]来改进基于DF的CBF的DOA性能。如图所示,DF处理使用频率f处的阵列数据和f +Δf处的复共轭数据的Hadamard乘积。
本文提出了三种联合收割机组合多个时间和测向样本的方法:时间、频率和时频联合。时间-DF-MUSIC对单个DF使用多个时间样本以获得时间平均样本协方差矩阵(SCM)。利用DF会产生不需要的伪影DOA [21]、[22]、[24],其取决于真实DOA和DF频率。由于伪影DOA在DF上变化,因此单独获得每个DF的MUSIC频谱并在频率上求平均可减轻伪影。
频率-DF-MUSIC使用均匀间隔的多个DF,具有相同的DF以获得频率平均的SCM。对于真实DOA,恒定DF共享相同的导向矢量,并且多DF等效于多快照。频率处理采用多个DF,实现了单次快拍DOA估计。单次时间快拍方法对于时变波达方向是有用的。
时频DF-MUSIC联合收割机将所有时间和DF样本合并到SCM中。该方法利用更多的数据平均来改善DOA估计。
文章插图


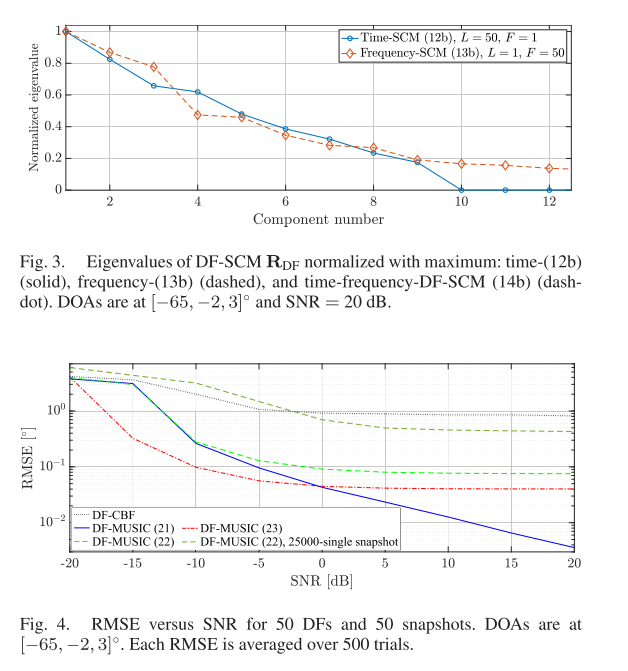
结论
推导了一种对多个频率的高频源及其差频进行DOA估计的算法,以获得低频处理。由于DF低于混叠频率,因此这是无空间混叠的。时间-DF-MUSIC算法将时间样本合并到样本协方差矩阵中,得到每个DF处的MUSIC谱,并对谱进行平均以估计最终DOA。频率-DF-MUSIC适用于单次快照,并且不需要随时间的固定DOA。时频-DF-MUSIC算法综合了所有的时频信息,联合使用更多的数据量获得处理增益。
MATLAB代码展示
%%
clear; clc;
close all;
% addpath([cd,'/_common'])
% addpath(['../_common'])
errCut = 10; % Maximum RMSE cut-off.
% rngNumber = 1; rng(rngNumber);
dbstop if error;
run_bpdn = 0;
%%
% Environment parameters
% c = 1500; % speed of sound
c = 343; % speed of sound
dfreq = 10000; % difference frequency [Hz]
% ULA-horizontal array configuration
d = .5*(c/dfreq); % intersensor spacing (based on DF)
% d = 3.75; % intersensor spacing [m]
% f = 200; % Hz -> 0.5 lambda = 0.5 * 1500 / 200 = 3.75 [m]
Nsensor = 20; % number of sensors
q = (0:1:(Nsensor-1))'; % sensor numbering
xq = (q-(Nsensor-1)/2)*d; % sensor locations
% 5-7.5 times to Difference Frequency (DF)
fmul1 = 5;
fmul2 = 7.5;
ftmp = linspace(fmul1*dfreq,fmul2*dfreq,50);
f = [ftmp,ftmp+dfreq]; % frequency [Hz]
Nfreq = numel(f);
lambda = c./f; % wavelength
% signal generation parameters
SNR = 20;
% total number of snapshots
Nsnapshot = 50;
% range of angle space
thetalim = [-90 90];
theta_separation = .005;
% Angular search grid
theta = (thetalim(1):theta_separation:thetalim(2))';
Ntheta = length(theta);
% Generate received signal
anglesTrue = [-40; 35];
fprintf(['True DOAs :',...repmat([' %.4f '],1,numel(anglesTrue)),'\n'],anglesTrue.')MATLAB仿真结果
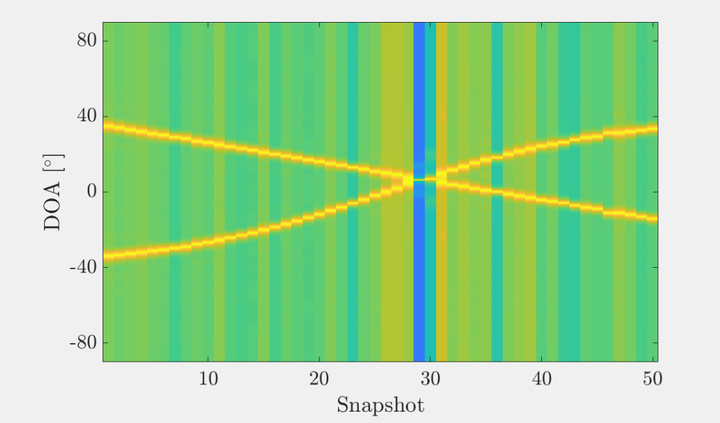
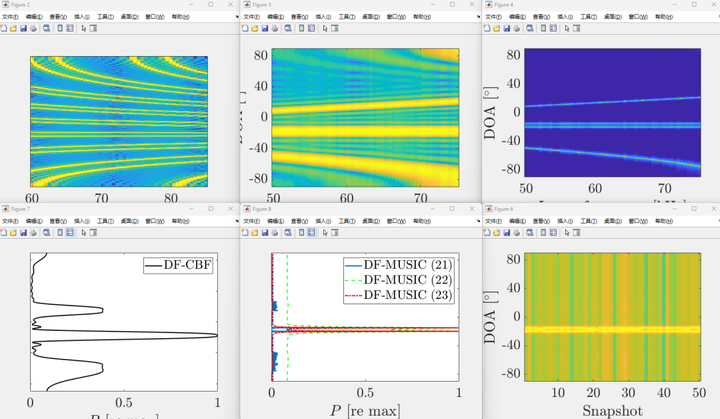
相关文章:

【测向定位】差频MUSIC算法DOA估计【附MATLAB代码】
微信公众号:EW Frontier QQ交流群:554073254 摘要 利用多频处理方法,在不产生空间混叠的情况下,估计出高频区域平面波的波达方向。该方法利用了差频(DF),即两个高频之间的差。这使得能够在可…...

智能车镜头组入门(四)元素识别
元素识别是摄像头部分中难度最大的一部分,也是我花时间最长的一部分,前前后后画了很长时间,最后还是勉勉强强完成了。 基础的元素识别主要有两个:十字,圆环,和斑马线。十字要求直行,圆环需要进…...

Java键盘输入语句
编程输入语句 1.介绍:在编程中,需要接受用户输入的数据,就可以使用键盘输入语句来获取。 2.步骤: 1)导入该类的所在包,java.util.* 2)创建该类对象(声明变量) 3)调用里面的功能 3…...

【读书笔记-《30天自制操作系统》-22】Day23
本篇内容比较简单,集中于显示问题。首先编写了应用程序使用的api_malloc,然后实现了在窗口中画点与画线的API与应用程序。有了窗口显示,还要实现关闭窗口的功能,于是在键盘输入API的基础上实现了按下按键关闭窗口。最后发现用上文…...
)
C++学习笔记(33)
三十五、栈 示例: #include <iostream> using namespace std; typedef int ElemType; // 自定义链栈的数据元素为整数。 struct SNode // 链栈的结点。 { ElemType data; // 存放结点的数据元素。 struct SNode* next; // 指向下一个结点的指针。 }; // 初始化…...

智谱清影 -CogVideoX-2b-部署与使用,带你揭秘生成6s视频的极致体验!
文章目录 1 效果展示2 CogVideoX 前世今生3 CogVideoX 部署实践流程3.1 创建丹摩实例3.2 配置环境和依赖3.3 模型与配置文件3.4 运行4 遇到问题 1 效果展示 A street artist, clad in a worn-out denim jacket and a colorful bandana, stands before a vast concrete wall in …...

探索Java中的设计模式:原则与实例
探索Java中的设计模式:原则与实例 大家好,我是微赚淘客系统3.0的小编,是个冬天不穿秋裤,天冷也要风度的程序猿!今天,我们将深入探讨Java中的设计模式,包括一些关键的设计原则和具体的实例。设计…...

【Java】关键字-static【主线学习笔记】
文章目录 前言关键字:static静态变量静态方法设置为静态的场景 下一篇 前言 Java是一门功能强大且广泛应用的编程语言,具有跨平台性和高效的执行速度,广受开发者喜爱。在接下来的学习过程中,我将记录学习过程中的基础语法、框架和…...
数字自然资源领域的实现路径
在数字化浪潮的推动下,自然资源的管理与利用正经历着前所未有的变革。本文将从测绘地理信息与遥感专业的角度,深度分析数字自然资源领域的实现路径。 1. 基础数据的数字化 数字自然资源的构建,首先需要实现基础数据的数字化。这包括地形地貌…...

GitLab邮箱发送邮件:如何实现自动化发信?
gitlab邮箱发送邮件设置教程?Gitlab邮箱配置和使用? GitLab不仅提供了代码版本控制、持续集成/持续部署等功能,还支持通过其内置的邮件功能实现自动化邮件发送。AokSend将深入探讨如何在GitLab中配置和使用邮箱发送邮件功能。 GitLab邮箱发…...
sqli-labs靶场搭建
下载了一个phpstudy进行搭靶场搭建 然后打开phpstudy安装好php,mysql等环境 正式sqli-labs靶场搭建 第一步:下载源码:https://codeload.github.com/Audi-1/sqli-labs/zip/master 解压后放进网站根目录,进到 sqli-labs的文件夹下࿰…...

Leetcode Hot 100刷题记录 -Day14(矩阵置0)
矩阵置0 问题描述: 给定一个 m x n 的矩阵,如果一个元素为 0 ,则将其所在行和列的所有元素都设为 0。 示例 1: 输入:matrix [[1,1,1],[1,0,1],[1,1,1]] 输出:[[1,0,1],[0,0,0],[1,0,1]]示例 2:…...

每日刷题(算法)
我们N个真是太厉害了 思路: 我们先给数组排序,如果最小的元素不为1,那么肯定是吹牛的,我们拿一个变量记录前缀和,如果当前元素大于它前面所有元素的和1,那么sum1是不能到达的值。 代码: #def…...

大牛直播SDK核心音视频模块探究
技术背景 视沃科技旗下”大牛直播SDK”,始于2015年,致力于传统行业极致体验的音视频直播技术解决方案,产品涵盖跨平台的实时RTMP推流、RTMP/RTSP直播播放(支持RTSP|RTMP H.265,Enhanced RTMP H.265)、GB28181设备接入、推送端播放…...

gin配置swagger文档
一、基本准备工作 1、安装依赖包 go get -u github.com/swaggo/swag/cmd/swag go get -u github.com/swaggo/gin-swagger go get -u github.com/swaggo/files2、在根目录上配置swagger的路由文件 //2.初始化路由router : initialize.Routers()// 配置swaggerdocs.SwaggerInfo…...

基于ssm的快餐店点餐系统设计与实现
需要项目源码请联系我,目前有各类成品 毕设 javaweb ssh ssm springboot等等项目框架,源码丰富。 专业团队,咨询就送开题报告,活动限时免费,有需要的朋友可以来留言咨询。 一、摘要 进入二十一世纪以来,计…...

集合框架底层使用了什么数据结构
1.是什么 集合框架(Collection Framework)是Java标准库的一部分,它提供了一系列接口和实现类,用于处理不同类型的集合。这些集合可以用于存储和操作对象,如列表、集合、映射等。集合框架的底层数据结构是多种多样的&am…...
Activiti7《第二式:破剑式》——工作流中的以柔克刚
冲冲冲!开干 这篇文章将分为九个篇章,带你逐步掌握工作流的核心知识。这篇文章将带你深入探讨工作流中的 “破剑式”,揭示如何通过 柔与刚 的结合来破解工作流的复杂性。本篇包含了 Activiti7 环境的进一步优化和表结构的深入分析࿰…...

docker快速搭建kafka
1、拉取镜像 kafka和 zk镜像 docker pull wurstmeister/zookeeper docker pull wurstmeister/kafka:1.1.02、运行zk容器 docker run -itd --restart always --name zookeeper -p 2181:2181 wurstmeister/zookeeper3、运行kafka容器 192.168.31.112 这个地址为zk地址 docker…...
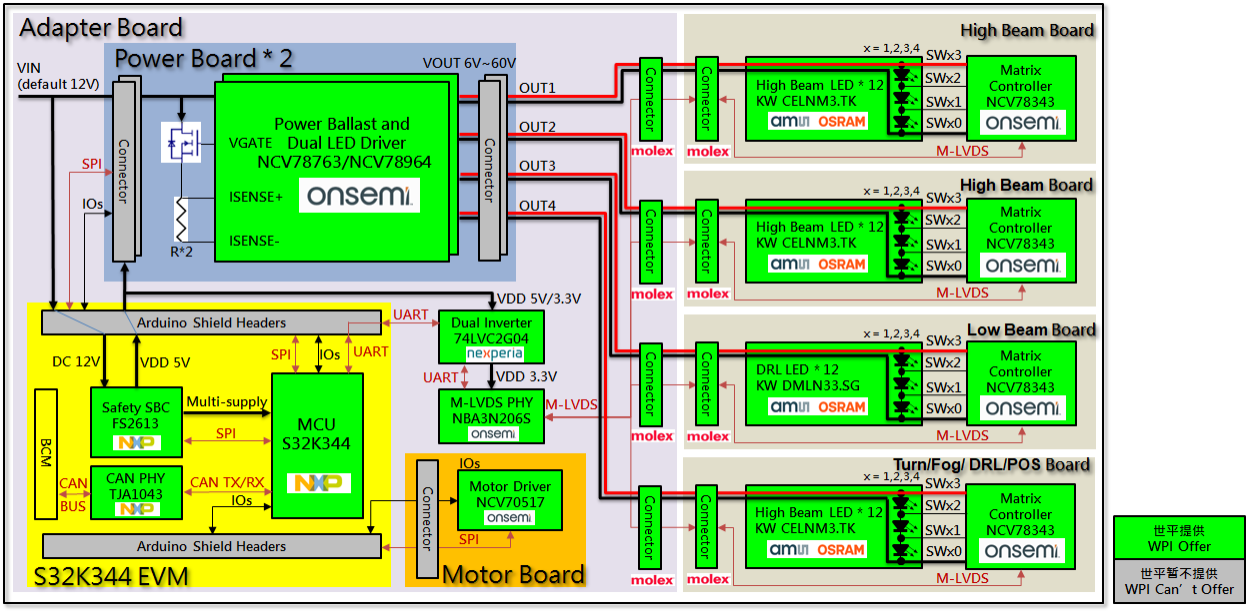
基于 onsemi NCV78343 NCV78964的汽车矩阵式大灯方案
一、方案描述 大联大世平集团针对汽车矩阵大灯,推出 基于 onsemi NCV78343 & NCV78964的汽车矩阵式大灯方案。 开发板搭载的主要器件有 onsemi 的 Matrix Controller NCV78343、LED Driver NCV78964、Motor Driver NCV70517、以及 NXP 的 MCU S32K344。 二、开…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

GC1808高性能24位立体声音频ADC芯片解析
1. 芯片概述 GC1808是一款24位立体声音频模数转换器(ADC),支持8kHz~96kHz采样率,集成Δ-Σ调制器、数字抗混叠滤波器和高通滤波器,适用于高保真音频采集场景。 2. 核心特性 高精度:24位分辨率,…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...

rknn toolkit2搭建和推理
安装Miniconda Miniconda - Anaconda Miniconda 选择一个 新的 版本 ,不用和RKNN的python版本保持一致 使用 ./xxx.sh进行安装 下面配置一下载源 # 清华大学源(最常用) conda config --add channels https://mirrors.tuna.tsinghua.edu.cn…...

aardio 自动识别验证码输入
技术尝试 上周在发学习日志时有网友提议“在网页上识别验证码”,于是尝试整合图像识别与网页自动化技术,完成了这套模拟登录流程。核心思路是:截图验证码→OCR识别→自动填充表单→提交并验证结果。 代码在这里 import soImage; import we…...

TCP/IP 网络编程 | 服务端 客户端的封装
设计模式 文章目录 设计模式一、socket.h 接口(interface)二、socket.cpp 实现(implementation)三、server.cpp 使用封装(main 函数)四、client.cpp 使用封装(main 函数)五、退出方法…...
