leetcode41. 缺失的第一个正数,原地哈希表
leetcode41. 缺失的第一个正数
给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。
请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。
示例 1:
输入:nums = [1,2,0]
输出:3
解释:范围 [1,2] 中的数字都在数组中。
示例 2:
输入:nums = [3,4,-1,1]
输出:2
解释:1 在数组中,但 2 没有。
示例 3:
输入:nums = [7,8,9,11,12]
输出:1
解释:最小的正数 1 没有出现。

目录
- leetcode41. 缺失的第一个正数
- 题目分析
- 算法介绍
- 算法步骤
- 算法流程
- 算法代码
- 算法分析
- 相似题目
题目分析
这是一个关于数组处理的问题。题目要求实现一个函数firstMissingPositive,该函数接受一个整数数组nums,并返回数组中第一个缺失的正整数。
算法介绍
为了解决这个问题,我们可以使用一种特殊的标记方法。首先,我们将所有小于等于0的元素替换为n+1,其中n是数组的长度。然后,我们遍历数组,将每个元素的正负号反转,如果它是一个正数。通过这种方式,我们可以标记数组中出现的所有正整数。最后,我们再次遍历数组,找到第一个未标记的正整数,即为答案。
算法步骤
- 遍历数组
nums,将所有小于等于0的元素替换为n+1。 - 再次遍历数组
nums,反转每个元素的正负号,如果它是一个正数。 - 第三次遍历数组
nums,找到第一个未标记的正整数,即为答案。
算法流程
算法代码
class Solution {
public:int firstMissingPositive(vector<int>& nums) {int n = nums.size();for (int& num: nums) {if (num <= 0) {num = n + 1;}}for (int i = 0; i < n; ++i) {int num = abs(nums[i]);if (num <= n) {nums[num - 1] = -abs(nums[num - 1]);}}for (int i = 0; i < n; ++i) {if (nums[i] > 0) {return i + 1;}}return n + 1;}
};
算法分析
- 时间复杂度:O(n),其中n是数组
nums的长度。我们只需要遍历数组三次。 - 空间复杂度:O(1),因为除了输入数组外,我们只使用了常数个额外空间。
- 易错点:
- 确保正确地将所有小于等于0的元素替换为
n+1。 - 在反转正负号时,确保只对正数进行操作。
- 确保正确地将所有小于等于0的元素替换为
相似题目
| 题目 | 链接 |
|---|---|
| 缺失的第一个正数 | LeetCode 41 |
| 缺失的数字 | LeetCode 268 |
请注意,以上表格仅为示例,实际链接可能需要根据具体平台和题目编号进行调整。
相关文章:

leetcode41. 缺失的第一个正数,原地哈希表
leetcode41. 缺失的第一个正数 给你一个未排序的整数数组 nums ,请你找出其中没有出现的最小的正整数。 请你实现时间复杂度为 O(n) 并且只使用常数级别额外空间的解决方案。 示例 1: 输入:nums [1,2,0] 输出:3 解释…...

如何准备教师资格证科目三“学科知识与教学能力”的考试与面试?(理科导向:数学/物理)
如何准备教师资格证科目三“学科知识与教学能力”的考试与面试?(理科导向:数学/物理) 目录 收起 1 前言 1.1 自身经历 1.2 教师资格证的作用 2 知识点题型分数的分布与学习建议 2.1 科目三的知识点分数分布: …...

3.数据类型
作业系统链接 Python 是一门面向对象友好的语言,支持多种内置数据类型,包括整数(int)、浮点数(float)、布尔值(bool)、字符串(str)、列表(list&am…...

Xcode报错:No exact matches in reference to static method ‘buildExpression‘
Xcode报错1:No exact matches in reference to static method buildExpression Xcode报错2:Type () cannot conform to View 这两个报错都是因为在SwiftUI的View的Body里面使用了ForEach循环,却没有在ForEach循环闭包的内部返回视图,而是做了…...

校园安全无小事,EasyCVR视频综合管理平台助力智慧校园视频监控系统全面升级
随着信息技术的飞速发展,智慧校园作为教育信息化的重要载体,正逐步成为提升校园安全管理、优化教育资源配置、增强师生互动体验的关键手段。其中,高效、智能的视频监控系统作为智慧校园不可或缺的一部分,扮演着至关重要的角色。TS…...

通过Python代码发送量化交易信号邮件通知
量化交易利用数学模型和计算机算法来分析市场数据,并生成交易信号,本文将介绍如何使用Python编写一个简单的脚本,通过发送邮件通知量化交易信号。 开启SMTP服务 首先要在发件箱的邮件设置中,将POP3/SMPT服务开启,记录下授权密码,在本地可通过此密码登录,注意有效期和保…...

计算机毕业设计 乡村生活垃圾管理系统的设计与实现 Java+SpringBoot+Vue 前后端分离 文档报告 代码讲解 安装调试
🍊作者:计算机编程-吉哥 🍊简介:专业从事JavaWeb程序开发,微信小程序开发,定制化项目、 源码、代码讲解、文档撰写、ppt制作。做自己喜欢的事,生活就是快乐的。 🍊心愿:点…...

Qwen 2.5:阿里巴巴集团的新一代大型语言模型
Qwen 2.5:阿里巴巴集团的新一代大型语言模型 摘要: 在人工智能领域,大型语言模型(LLMs)的发展日新月异,它们在自然语言处理(NLP)和多模态任务中扮演着越来越重要的角色。阿里巴巴集…...

Element UI入门笔记(个人向)
Element UI入门笔记 将页面分割为一级菜单、二级菜单、导航栏三个部分;使用npm下载安装,使用语句npm i element-ui -s; 布局组件 el-form 用于创建和管理表单;从属性上看: :model:用于双向数据绑定,将表单…...

网络通信失败-关闭网络防火墙
0、报错描述1、分析2、解决办法 0、报错描述 在进行树莓派和PC端的网络通信的时候, 使用树莓派作为服务端,PC端作为客户端的时候,能成功通讯。 使用树莓派作为客户端,PC端作为服务端的时候,却发现通信失败。 体现在没…...

基于kolla-ansible在openEuler 22.03 SP4上部署OpenStack-2023.2
测试环境 openEuler-22.03-LTS-SP4-x86_64-dvd.iso Virtual Box,4 vCPU, 8G RAM, 50 vDisk。安装时删除/home,SWAP分区,全部空间给/目录。 目标是部署OpenStack All-In-One模式,控制节点计算节点存储节点在一台机器实现。 系统配…...

深拷贝|浅拷贝
目录 1. 深拷贝(Deep Copy) 2. 浅拷贝(Shallow Copy) 3. 深拷贝和浅拷贝的区别 4. 示例代码 浅拷贝示例 深拷贝示例 5.常用的方法 1.Java Object.clone() 方法 2.序列化与反序列化 6.Spring Boot 中的常用方法 使用 Se…...

图像处理-掩码
文章目录 一、简介二、主要用途三、代码实现四、掩码优缺点1.优点2.缺点 一、简介 在图像处理中,掩码(Mask)是一种特殊的图像,用于指定对原始图像进行操作的区域。掩码通常是二值图像(即图像上的每个像素只有两个可能…...

[2025]基于微信小程序慢性呼吸系统疾病的健康管理(源码+文档+解答)
博主介绍: ✌我是阿龙,一名专注于Java技术领域的程序员,全网拥有10W粉丝。作为CSDN特邀作者、博客专家、新星计划导师,我在计算机毕业设计开发方面积累了丰富的经验。同时,我也是掘金、华为云、阿里云、InfoQ等平台…...

react之jsx基础(1)概念和本质
文章目录 JSX 的基本概念1. **语法**2. **表达式**3. **属性**4. **子元素** JSX 的编译过程1. **转换成 JavaScript**2. **React 元素** JSX 的实际应用1. **组件定义**2. **组件嵌套** 总结 当然,以下是对 JSX 的详细讲解,包括其基本概念、语法、编译过…...

sqli-labs靶场自动化利用工具——第13关
文章目录 概要整体架构流程技术细节执行效果小结 概要 Sqli-Labs靶场对于网安专业的学生或正在学习网安的朋友来说并不陌生,或者说已经很熟悉。那有没有朋友想过自己开发一个测试脚本能实现自动化化测试sqli-labs呢?可能有些人会说不是有sqlmap&#…...

大舍传媒:尼日利亚传统新闻媒体宣传助力新兴行业蓬勃发展
大舍传媒:尼日利亚传统新闻媒体宣传助力新兴行业蓬勃发展 在全球化的浪潮下,媒体作为信息传播的重要渠道,对于促进行业发展和推动社会进步扮演着举足轻重的角色。特别是在非洲大陆上人口最多、经济最发达的国家——尼日利亚,传统…...
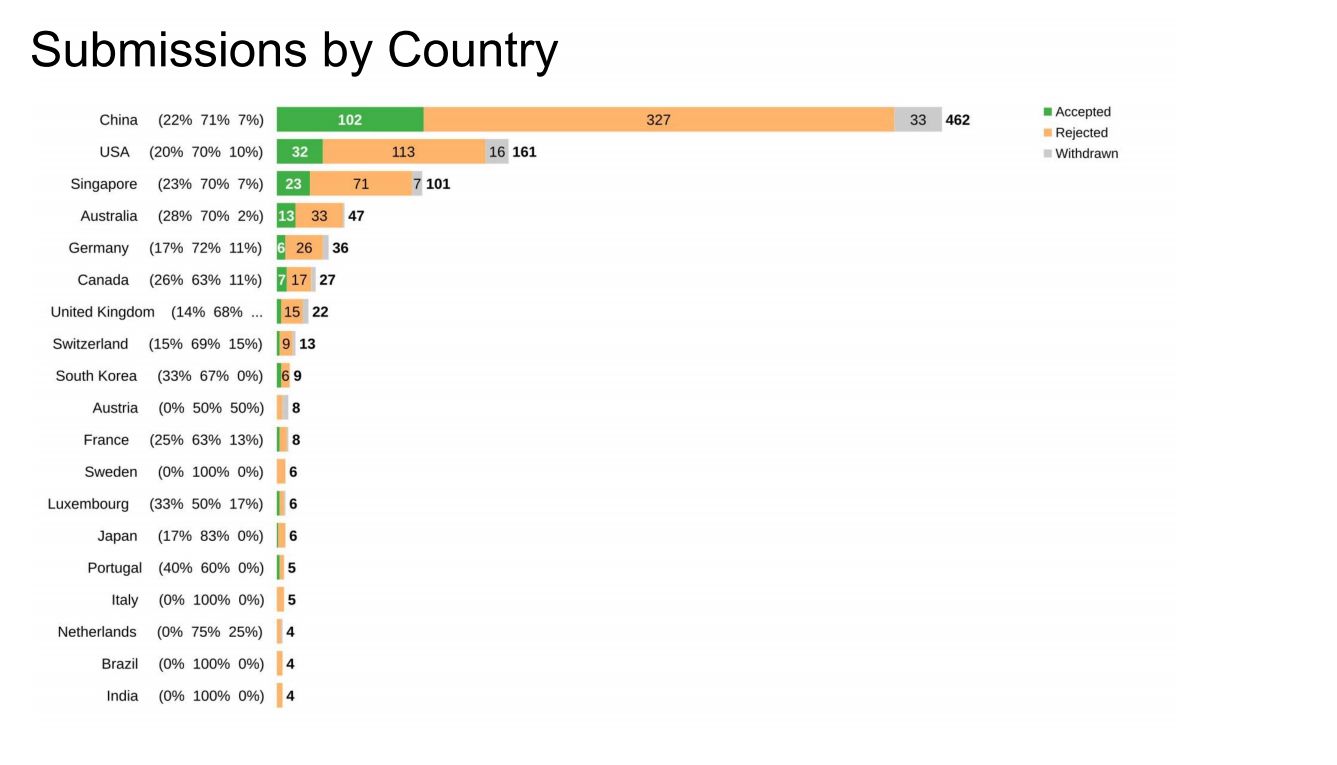
ISSTA 2024盛大开幕:中国学者的录取数和投稿量均位列第一
随着夏日的尾声,全球软件测试领域的专家和学者齐聚在奥地利维也纳。共同参与这场科技盛宴——ISSTA 2024。这场国际会议正如火如荼地进行中,吸引了来自世界各地的专业人士参与。 会议实况: 9月16日与17日,大会安排了丰富的社交活…...

HttpMediaTypeNotAcceptableException: No acceptable representation问题解决方法
Background org.springframework.web.HttpMediaTypeNotAcceptableException: Could not find acceptable representation HttpMediaTypeNotAcceptableException: No acceptable representation 异常通常发生在Web应用程序中,客户端请求了一个资源,但是…...

Scrapy爬虫框架 Pipeline 数据传输管道
在网络数据采集领域,Scrapy 是一个非常强大的框架,而 Pipeline 是其中不可或缺的一部分。它允许我们在数据处理的最后阶段对抓取的数据进行进一步的处理,如清洗、存储等操作。 本教程将详细介绍如何在 Scrapy 中使用 Pipeline,帮…...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...

云原生周刊:k0s 成为 CNCF 沙箱项目
开源项目推荐 HAMi HAMi(原名 k8s‑vGPU‑scheduler)是一款 CNCF Sandbox 级别的开源 K8s 中间件,通过虚拟化 GPU/NPU 等异构设备并支持内存、计算核心时间片隔离及共享调度,为容器提供统一接口,实现细粒度资源配额…...

QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下,音视频内容犹如璀璨繁星,点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频,到在线课堂中知识渊博的专家授课,再到影视平台上扣人心弦的高清大片,音…...
