进制转换,原码,反码,补码,二进制位运算及应用
进制转换
2B(0--1),8O(0--7),10D,16H(0——9,A——F)
8位二进制数,左边高位,右边低位

2,8,16 -> 10进制整数,小数
- 整数:从后往前,依次(每位)* 进制(2,8,16) ^ (0++),最后求和
- 小数:从前往后,依次(从小数点后每位)* 进制(2,8,16) ^ (-1- -),最后求和
- 最后整体求和

10 ->2,8,16进制整数,小数
- 整数:不断除进制(2,8,16),直到商为0,反向读取余数
- 小数:不断乘进制(2,8,16),向下取整,正向读取,写在小数点后,每次执行都获得一个精度
- 和整数部分同时输出

2 -> 8,16进制
- 2 -> 8从后往前,每3位合为一个二进制位
- 2 -> 16从后往前,每4位合为一个二进制位
8,16 -> 2进制
- 8 -> 2每一个八进制位转换为3个二进制
- 16 -> 2每一个十六进制位转换为4个二进制
8 ->16进制
- 通过2/10进制间接转换
原码,反码,补码
原码:对于signed的整数,最高位是符号位:正(0)负(1),其余为是数值的绝对值,对于加减运算操作不友好,需要通过反码或补码来完成
反码:正数和原码一致,负数为十进制形式的绝对值按位取反,符号位不变,表示-128(对于8位时)
补码:正数和原码一致,负数为反码 + 1
有效范围
unsigned无符号8位,0——255
signed有符号8位,- 128——127
每增一位,都是前一位的2倍
二进制运算
计算机运算都是以二进制补码形式
加法:
5 + 1 都是正数,正数原反补都一致,对应位相加,
0 + 0 = 0, 0 + 1 / 1 + 0 = 1, 1 + 1 = 2->转为2进制 = 10(进一位), 1 + 1 + 1 = 3->转为2进制 = 11(进一位)
减法:
5 - 1 = 5 + (-1),5的补码和原码一致0101,-1的补码计算得到1111,
因此相加=10100,忽略最高位,为4
位运算
我们直到计算机都是以二进制形式存储,因为对位的操作,比普通运算符要快许多,因此尽量使用位运算代替普通运算符
位运算符

常见位操作


常见的位十进制操作
乘除法
a << 1 ≡ a ∗ 2
a >> 1 ≡ a / 2 交换整形变量值
void swap(int &a,int &b){a ^= b;b ^= a;a ^= b;}
判断奇数偶数
a & 1对负数取绝对值
~ a + 1相关文章:

进制转换,原码,反码,补码,二进制位运算及应用
进制转换 2B(0--1),8O(0--7),10D,16H(0——9,A——F) 8位二进制数,左边高位,右边低位 2,8,16 -> 10进制整数,小数 整数:从后往…...

node.js居家养老服务系统—计算机毕业设计源码35247
目 录 摘要 1 绪论 1.1选题的背景 1.2研究的意义 1.3国内外居家养老信息化管理现状分析 1.4 express框架介绍 1.5node.js功能模块 1.6论文结构与章节安排 2 居家养老服务系统系统分析 2.1 可行性分析 2.2 系统流程分析 2.2.1数据增加流程 2.2.2数据修改流程 2.2.…...

OpenHarmony(鸿蒙南向开发)——小型系统芯片移植指南(二)
往期知识点记录: 鸿蒙(HarmonyOS)应用层开发(北向)知识点汇总 鸿蒙(OpenHarmony)南向开发保姆级知识点汇总~ OpenHarmony(鸿蒙南向开发)——轻量系统芯片移植指南(一) Op…...

Live800:从心出发,以情动人:构建深度客户服务文化
在当今这个竞争激烈的市场环境中,企业之间的较量已不仅仅局限于产品质量的比拼,更在于谁能提供更优质、更贴心的客户服务。在这个背景下,“从心出发,以情动人”成为了构建深度客户服务文化的核心理念,它要求企业不仅要…...

分布式事务一致性:本地消息表设计与实践
概念 本地消息表是一种常见的解决分布式事务问题的方法。其核心思想是将分布式事务拆分成本地事务来处理,通过消息队列来保证各个本地事务的最终一致性。 实现步骤 创建本地消息表:在数据库中创建一个本地消息表,用于存储待发送的消息以及消…...

深入浅出Docker
1. Docker引擎 Docker引擎是用来运行和管理容器的核心软件。通常人们会简单的将其指代为Docker或Docker平台。 基于开放容器计划(OCI)相关的标准要求,Docker引擎采用了模块化的设计原则,其组件是可替换的。 Docker引擎由如下主…...

Flink 与 Kubernetes (K8s)、YARN 和 Mesos集成对比
Flink 与 Kubernetes (K8s)、YARN 和 Mesos 的紧密集成,是 Flink 能够在不同分布式环境中高效运行的关键特性。 Flink 提供了与这些资源管理系统的深度集成,以便在多种集群管理环境下提交、运行和管理 Flink 作业。Flink 与 K8s、YARN 和 Mesos 集成的详…...

Python 集合的魔法:解锁高效数据处理的秘密
引言 集合作为 Python 的一种内置数据类型,其本质是一个无序且不重复的元素序列。虽然表面上看它似乎只是列表或元组的一种变体,但实际上,集合背后有着更为高效的查找机制。通过学习和掌握集合的高级操作,我们不仅能更好地理解 P…...

Go必知必会:构建复杂数据模型的基石
Go语言以其清晰的语法和强大的内置类型系统,为构建高效且易于维护的软件程序提供了坚实的基础。在Go的数据类型体系中,结构体(struct)扮演着至关重要的角色,它是实现复杂数据模型的关键工具。结构体允许开发者将多个不…...

大数据Flink(一百一十七):Flink SQL的窗口操作
文章目录 Flink SQL的窗口操作 一、窗口的概述 二、Group Windows 1、滚动窗口(TUMBLE) 2、滑动窗口(HOP) 3、Session 窗口(SESSION&am…...

【西电电装实习】6. 手装无人机的蓝牙断连debug
文章目录 前言零、闪灯状态零零、翻滚角,俯仰角,偏航角一、问题描述二、现象解释三、解决方案参考文献 前言 在 西电无人机电装实习 时遇到的问题使用蓝牙芯片 CH582F。沁恒的蓝牙芯片CH582F是一款集成了BLE(Bluetooth Low Energy࿰…...

AIGC实战之如何构建出更好的大模型RAG系统
大家好,我是爱编程的喵喵。双985硕士毕业,现担任全栈工程师一职,热衷于将数据思维应用到工作与生活中。从事机器学习以及相关的前后端开发工作。曾在阿里云、科大讯飞、CCF等比赛获得多次Top名次。现为CSDN博客专家、人工智能领域优质创作者。…...

【数据结构-差分】力扣1589. 所有排列中的最大和
有一个整数数组 nums ,和一个查询数组 requests ,其中 requests[i] [starti, endi] 。第 i 个查询求 nums[starti] nums[starti 1] … nums[endi - 1] nums[endi] 的结果 ,starti 和 endi 数组索引都是 从 0 开始 的。 你可以任意排列…...

Spark部署文档
Spark Local环境部署 下载地址 https://dlcdn.apache.org/spark/spark-3.2.0/spark-3.2.0-bin-hadoop3.2.tgz 条件 PYTHON 推荐3.8JDK 1.8 Anaconda On Linux 安装 本次课程的Python环境需要安装到Linux(虚拟机)和Windows(本机)上 参见最下方, 附: Anaconda On Linux 安…...

Broadcast:Android中实现组件及进程间通信
目录 一,Broadcast和BroadcastReceiver 1,简介 2,广播使用 二,静态注册和动态注册 三,无序广播和有序广播 1,有序广播的使用 2,有序广播的截断 3,有序广播的信息传递 四&am…...

5分钟熟练上手ES的具体使用
5分钟上手ES的具体使用 相信有很多同学想要去学习elk时会使用docker等一些方式去下载相关程序,但提到真正去使用es的一系列操作时又会知之甚少。于是这一篇博客应运而生。 本文就以下载好elk/efk系统后应该如何去使用为例,介绍es的具体操作。 es关键字…...

lambda 自调用递归
从前序与中序遍历序列构造二叉树 官方解析实在是记不住,翻别人的题解发现了一个有意思的写法 class Solution { public:TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {auto dfs [](auto&& dfs, auto&&…...
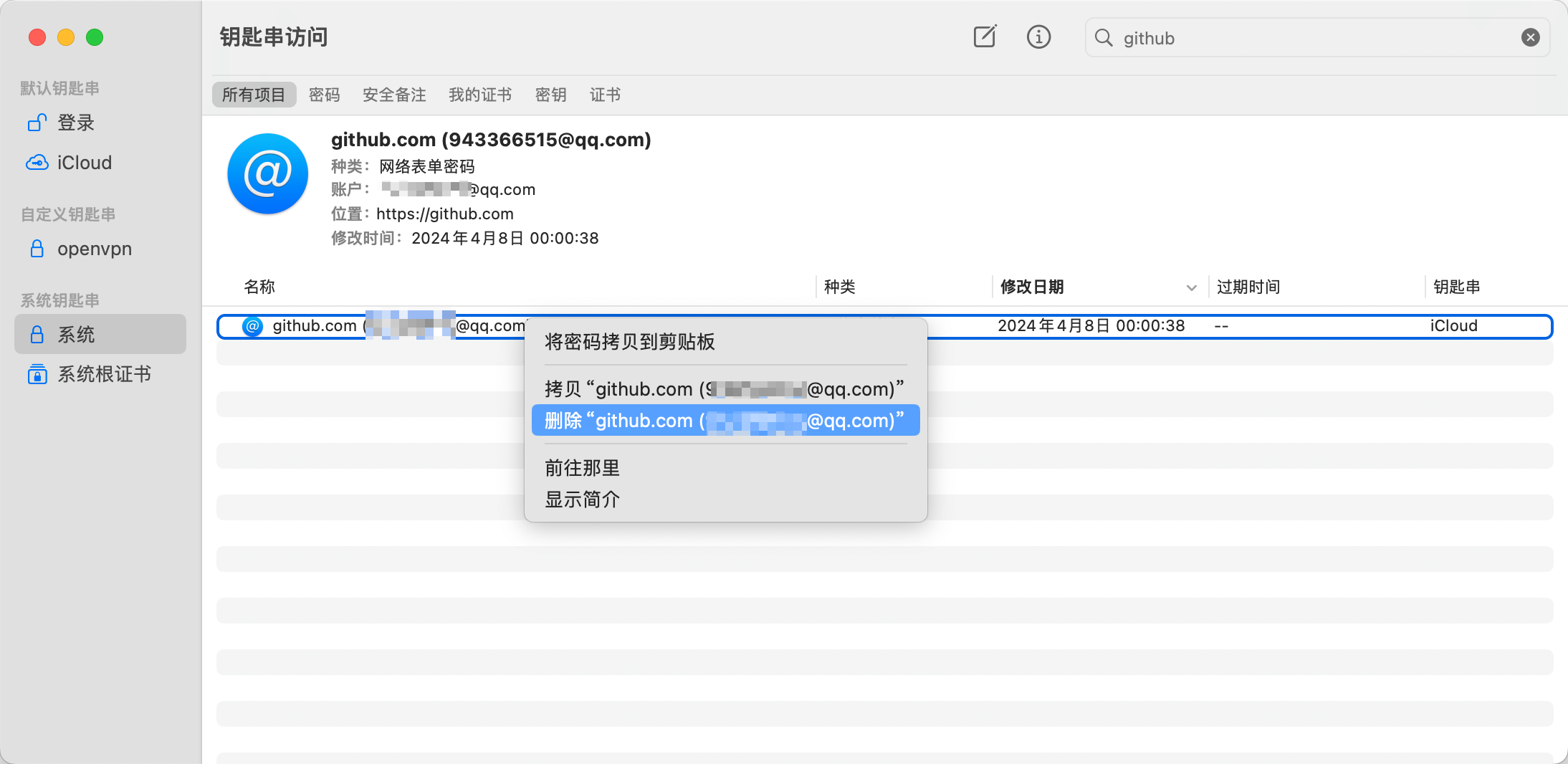
mac中git操作账号的删除
命令行玩的很溜的可以跳过 找到钥匙串访问 搜github、gitee就行了...

AI Agent的20个趋势洞察
结论整理自【QuestMobile2024 AI智能体应用洞察半年报】: AI原生应用(APP)一路高歌;豆包用户突破3000万;TOP10 APP以综合类应用为主。无论何种类型的AIGC APP都以智能体为“抓手”,专注于解决各种细分场景中的问题&am…...

Spring Boot-定时任务问题
Spring Boot 定时任务问题及其解决方案 1. 引言 在企业级应用中,定时任务是一项常见需求,通常用于自动化执行某些操作,如数据备份、日志清理、系统监控等。Spring Boot 提供了简洁易用的定时任务机制,允许开发者通过简单的配置来…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...
