蓝桥杯刷题第二十二天
第一题:受伤的皇后
题目描述
有一个 n×n 的国际象棋棋盘(n 行 n 列的方格图),请在棋盘中摆放 n 个受伤的国际象棋皇后,要求:
任何两个皇后不在同一行。
任何两个皇后不在同一列。
如果两个皇后在同一条 45 度角的斜线上,这两个皇后之间行号的差值至少为 3 。
请问一共有多少种摆放方案。
输入描述
输入的第一行包含一个整数 n。
其中,1≤n≤10。
输出描述
输出一个整数,表示答案。
输入
4输出
2深搜,对于每一行进行选择
check判断,列是否有
对角线是否有, 如果有,则行差值大于等于三
正对角线 行 + 列 == 该点 行 + 列
反对角线 行- 该点行 == 列 - 该点列
如果是dg,udg数组来表示
dg[x + y], udg[n - x + y]来判断,但是这种是正规皇后
#include<iostream>
using namespace std;const int N = 12;
int a[12]; //表示第i行元素在第几列
int n, ans;bool check(int row, int y){for(int i = 0 ; i < row; i++){if(a[i] == y) return false;if(a[i] + i == row + y && row - i < 3) return false;if(row - i == y - a[i] && row - i < 3) return false;}return true;
}void dfs(int u){if(u == n){ans++;return ;}for(int i = 0; i < n; i++){if(check(u, i)){a[u] = i;dfs(u + 1);a[u] = 0;} }
}int main(){cin>>n;dfs(0);cout<<ans<<endl;return 0;
}第二题:完全平方数
问题描述
一个整数 a 是一个完全平方数, 是指它是某一个整数的平方, 即存在一个 整数 b, 使得a=b2 。
给定一个正整数 n, 请找到最小的正整数 x, 使得它们的乘积是一个完全平 方数。
输入格式
输入一行包含一个正整数 n 。
输出格式
输出找到的最小的正整数 x 。
样例输入 1
12
样例输出 1
3
样例输入 2
15
样例输出 2
15
评测用例规模与约定
对于 30 的评测用例, 1≤n≤1000, 答案不超过 1000 。
对于 60 的评测用例, 1≤n≤108, 答案不超过 108 。
对于所有评测用例,1≤n≤1012, 答案不超过 1012 。
一个数是完全平方数,一定有他分解得质因数得指数一定是偶数
所以我们找到指数非偶数的质因数,然后再乘到res里面就得到的最小要乘的数
考察分解质因数
#include <iostream>
using namespace std;typedef long long LL;int main()
{long long n;cin>>n;LL res = 1;for(LL i = 2; i <= n / i; i++)if(n % i == 0){LL s = 0;while( n % i == 0) s ++ , n /= i;if(s % 2) res *= i;}if(n > 1) res *= n;cout<<res<<endl;return 0;
}相关文章:

蓝桥杯刷题第二十二天
第一题:受伤的皇后题目描述有一个 nn 的国际象棋棋盘(n 行 n 列的方格图),请在棋盘中摆放 n 个受伤的国际象棋皇后,要求:任何两个皇后不在同一行。任何两个皇后不在同一列。如果两个皇后在同一条 45 度角的…...
CentOS从gcc 4.8.5 升级到gcc 8.3.1
gcc -v查看当前gcc版本。 sudo yum install centos-release-scl-rh安装centos-release-scl-rh。 sudo yum install devtoolset-8-build安装devtoolset-8-build。 显示“Complete!”表示安装成功。 sudo yum install devtoolset-8-gdb安装devtoolset-8-gdb。 显示“Comple…...
【人人都能读标准】12. 原始类型的编码形式
本文为《人人都能读标准》—— ECMAScript篇的第12篇。我在这个仓库中系统地介绍了标准的阅读规则以及使用方式,并深入剖析了标准对JavaScript核心原理的描述。 ECMAScript有7种原始类型,分别是Undefined、Null、Boolean、String、Number、BigInt、Symbo…...

VUE进行前后端交互
目录 一、 跨域 1. 什么是跨域? 2. 什么是本域? 3. 浏览器请求的三种报错 二、SpringBoot解决跨域问题其他前后端跨域请求解决方案 1. SpringBoot上直接添加CrossOrigin 2. 处理跨域请求的Configuration 3. 采用过滤器的方式 3.1 方式一 3.2 方式…...

ThingsBoard Gateway:物联网设备数据采集与集成的强大解决方案
文章目录ThingsBoard Gateway:物联网设备数据采集与集成的强大解决方案1\. ThingsBoard Gateway:概述2\. 主要特点与优势3\. 应用场景4\. 如何使用ThingsBoard Gateway:物联网设备数据采集与集成的强大解决方案 随着物联网(IoT&a…...

什么是镜像/raid
镜像(Mirroring)是一种文件存储形式,是冗余的一种类型,一个磁盘上的数据在另一个磁盘上存在一个完全相同的副本即为镜像。可以把许多文件做成一个镜像文件,与GHOST等程序放在一个盘里用GHOST等软件打开后,又…...
【Python】如何有效比较两个时间序列在图形上的相似度?
文章目录前言一、1.准备二、实操1.使用Matplotlib可视化比较两个时间序列2.计算两个时间序列的相关系数:3.使用Python实现动态时间规整算法(DTW):总结前言 比较两个时间序列在图形上是否相似,可以通过以下方法&#x…...
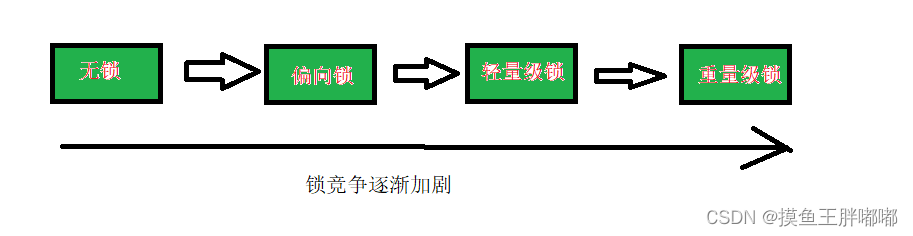
JavaEE-常见的锁策略和synchronized的锁机制
目录常见的锁策略乐观锁和悲观锁轻量级锁和重量级锁自旋锁和挂起等待锁普通互斥锁和读写锁公平锁和非公平锁可重入锁和不可重入锁synchronized的锁机制synchronized特性锁升级/锁膨胀锁消除锁粗化常见的锁策略 乐观锁和悲观锁 乐观锁和悲观锁主要是看主要是锁竞争的激烈程度.…...

信息化,数字化,智能化是三种不同的概念吗?
前两年流行“信息化”,网上铺天盖地都是关于“信息化”的文章,这两年开始流行起“数字化”,于是铺天盖地都是“数字化”的文章。(这一点从数字化和信息化这两个关键词热度趋势就可以看出来)。 但点开那些文章仔细看看…...
)
【华为OD机试 2023最新 】 匿名信(C++ 100%)
题目描述 电视剧《分界线》里面有一个片段,男主为了向警察透露案件细节,且不暴露自己,于是将报刊上的字减下来,剪拼成匿名信。 现在又一名举报人,希望借鉴这种手段,使用英文报刊完成举报操作。 但为了增加文章的混淆度,只需满足每个单词中字母数量一致即可,不关注每个…...
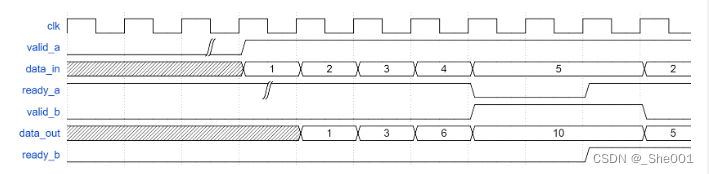
硬件语言Verilog HDL牛客刷题day05 时序逻辑部分
1.VL29 信号发生器 1.题目: 题目描述: 请编写一个信号发生器模块,根据波形选择信号wave_choise发出相应的波形:wave_choice0时,发出方波信号;wave_choice1时,发出锯齿波信号;wave…...

Ajax 入门
前端技术:在浏览器中执行的程序都是前端技术。如 html、css、js 等 后端技术:在服务器中执行的长须,使用 Java 等语言开发的后端程序。servlet,jsp,jdbc,mysql,tomacat 等 全局刷新 使用表单…...
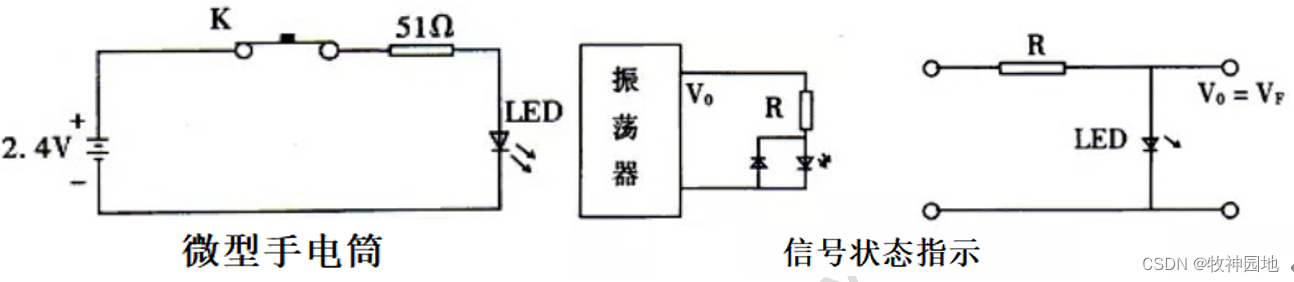
半导体器件基础06:发光二极管
说在开头:关于玻尔原子模型(1) 卢瑟福的模型面临着与经典电磁波理论的矛盾,按照经典电磁波理论,卢瑟福的原子不可能稳定存在超过1秒钟。玻尔面临着选择:要么放弃卢瑟福模型,要么放弃麦克斯韦伟…...

AutoCV第二课:Python基础
目录Python基础前言1.流程控制1.1 条件语句1.2 循环语句1.2.1 while循环语句1.2.2 for循环语句1.3 作业1.4 拓展-try except语法2.函数2.1 函数定义2.2 函数的参数2.2.1 位置参数2.2.2 命名参数2.2.3 默认参数2.2.4 可变参数2.2.5 参数展开2.3 递归函数2.3.1 递归函数定义2.3.2…...

LeetCode算法 打家劫舍 和 打家劫舍II C++
目录题目 打家劫舍参考答案题目 打家劫舍II参考答案题目 打家劫舍 你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯…...

蓝桥杯刷题冲刺 | 倒计时10天
作者:指针不指南吗 专栏:蓝桥杯倒计时冲刺 🐾马上就要蓝桥杯了,最后的这几天尤为重要,不可懈怠哦🐾 文章目录1.有边数限制的最短路2.九进制转十进制1.有边数限制的最短路 题目 链接: 853. 有边数…...

个人练习-Leetcode-剑指 Offer II 109. 开密码锁
题目链接:https://leetcode.cn/problems/zlDJc7/ 题目大意:给出一个四位数字的密码锁,初始状态是0000,目标是targer。每一次转动只能让一个位的轮盘转动一下(0往后转是9)。有一个vector<string> dea…...

四个常见的Linux面试问题
四个常见的Linux面试问题。 刚毕业要找工作了,只要是你找工作就会有面试这个环节,那么在面试环节中,有哪些注意事项值得我的关注呢?特别是专业技术岗位,这样的岗位询问一般都是在职的工程师,如何在面试环节…...

15、接口(C#)
15.1 什么是接口 接口是指定一组函数成员而不实现它们的引用类型。所以只能类和结构实现接口。 15.2 声明接口 接口声明不能包含以下成员 数据成员静态成员 接口声明只能包含以下类型的费静态成员函数声明: 方法事件索引器属性 这些函数成员的声明不能包含任何实…...
)
C++中常见的容器类使用方法举例(vector、deque、map、set)
cpp中常见的容器类有vector、list、deque、map、set、unordered_map和unordered_set。 下面将举例直接说明各个容器的使用方法。 文章目录综合示例1. vector:动态数组,支持随机访问2. list:双向链表,支持双向遍历和插入删除3. de…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

django blank 与 null的区别
1.blank blank控制表单验证时是否允许字段为空 2.null null控制数据库层面是否为空 但是,要注意以下几点: Django的表单验证与null无关:null参数控制的是数据库层面字段是否可以为NULL,而blank参数控制的是Django表单验证时字…...

Windows电脑能装鸿蒙吗_Windows电脑体验鸿蒙电脑操作系统教程
鸿蒙电脑版操作系统来了,很多小伙伴想体验鸿蒙电脑版操作系统,可惜,鸿蒙系统并不支持你正在使用的传统的电脑来安装。不过可以通过可以使用华为官方提供的虚拟机,来体验大家心心念念的鸿蒙系统啦!注意:虚拟…...

Linux中INADDR_ANY详解
在Linux网络编程中,INADDR_ANY 是一个特殊的IPv4地址常量(定义在 <netinet/in.h> 头文件中),用于表示绑定到所有可用网络接口的地址。它是服务器程序中的常见用法,允许套接字监听所有本地IP地址上的连接请求。 关…...

GB/T 43887-2024 核级柔性石墨板材检测
核级柔性石墨板材是指以可膨胀石墨为原料、未经改性和增强、用于核工业的核级柔性石墨板材。 GB/T 43887-2024核级柔性石墨板材检测检测指标: 测试项目 测试标准 外观 GB/T 43887 尺寸偏差 GB/T 43887 化学成分 GB/T 43887 密度偏差 GB/T 43887 拉伸强度…...

VSCode 没有添加Windows右键菜单
关键字:VSCode;Windows右键菜单;注册表。 文章目录 前言一、工程环境二、配置流程1.右键文件打开2.右键文件夹打开3.右键空白处打开文件夹 三、测试总结 前言 安装 VSCode 时没有注意,实际使用的时候发现 VSCode 在 Windows 菜单栏…...
