代码随想录算法训练营DAY09之动态规划(一)基础题目
理论基础:
如果某一问题有很多重叠子问题,使用动态规划是最有效的。
动态规划中每一个状态一定是由上一个状态推导出来的,这一点就区分于贪心,贪心没有状态推导,而是从局部直接选最优的。
例子:
例如:有N件物品和一个最多能背重量为W 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
动态规划中dp[j]是由dp[j-weight[i]]推导出来的,然后取max(dp[j], dp[j - weight[i]] + value[i])。
但如果是贪心呢,每次拿物品选一个最大的或者最小的就完事了,和上一个状态没有关系。
所以贪心解决不了动态规划的问题。
动规五部曲:
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
并不只是找到递推公式便完事大吉了,五步都很重要
如何debug:
打印dp数组的日志!以下灵魂三问:
- 这道题目我举例推导状态转移公式了么?
- 我打印dp数组的日志了么?
- 打印出来了dp数组和我想的一样么?
509.斐波拉契数
力扣题目链接
题意:
给定n,求F(n),0<=n<=30
虽然比较简单,但是正是因为简单,可以用来练习方法论,为难题打好基础
五部曲:
1.dp[i]的定义为:第i个数的斐波那契数值是dp[i]
2.递推公式:dp[i] = dp[i - 1] + dp[i - 2];
3.dp的初始化:
dp[0] = 0;
dp[1] = 1;4. 确定遍历顺序:从递归公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出,dp[i]是依赖 dp[i - 1] 和 dp[i - 2],那么遍历的顺序一定是从前到后遍历的
5.举例推导dp数组
如果不对就打印日志
代码(1)
class Solution {
public:int fib(int N) {if (N <= 1) return N;vector<int> dp(N + 1);dp[0] = 0;dp[1] = 1;for (int i = 2; i <= N; i++) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[N];}
};代码(2)
其实我们只需要维护两个数值就可以了,不需要记录整个序列。以降低空间复杂度到O(1)
class Solution {
public:int fib(int N) {if (N <= 1) return N;int dp[2];dp[0] = 0;dp[1] = 1;for (int i = 2; i <= N; i++) {int sum = dp[0] + dp[1];dp[0] = dp[1];dp[1] = sum;}return dp[1];}
};代码(3)递归
但是时间复杂度从O(n)变成了O(2^n)
class Solution {
public:int fib(int N) {if (N < 2) return N;return fib(N - 1) + fib(N - 2);}
};70.爬楼梯
力扣题目链接
题意:
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
五步曲:
1.dp[i],爬到第i层的方法
2.递推公式:dp[i]=dp[i-1]+dp[i-2],因为到每一层只可能是从前一层爬一步或者前两层爬两步爬上来的,这里可以发现这道题跟斐波拉契那道题一样。
3.初始化:dp[1]=1;dp[2]=2;
4.确定遍历顺序:从前往后
5.举例√
overover,下面放代码
代码(优化)
class Solution {
public:int climbStairs(int n) {if (n <= 1) return n;int dp[3];dp[1] = 1;dp[2] = 2;for (int i = 3; i <= n; i++) {int sum = dp[1] + dp[2];dp[1] = dp[2];dp[2] = sum;}return dp[2];}
};746、使用最小花费爬楼梯
力扣题目链接
题意:
给你一个整数数组 cost ,其中 cost[i] 是从楼梯第 i 个台阶向上爬需要支付的费用。一旦你支付此费用,即可选择向上爬一个或者两个台阶。
你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。
请你计算并返回达到楼梯顶部的最低花费。
五步曲:
1.含义:到i的最小花费
2.公式dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
3.初始化,dp[0]=dp[1]=0;
4.确定顺序:从前往后
5.举例看对不对√
代码(优化):
class Solution {
public:int minCostClimbingStairs(vector<int>& cost) {int n=cost.size();vector<int>dp(5);dp[0]=dp[1]=0;for(int i=2;i<=n;i++){dp[2]=min((dp[1]+cost[i-1]),(dp[0]+cost[i-2]));dp[0]=dp[1];dp[1]=dp[2];}return dp[2];}
};62、不同路径
力扣题目链接
题意:
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
五步曲:
1.dp[i][j]表示到达该坐标的路径数
2.只能从左边和上面来,所以dp[i][j] = dp[i - 1][j] + dp[i][j - 1]
3.初始化,要初始整个第一列和第一行
4.顺序,正常的就行
5.举例OK
代码:
class Solution {
public:int uniquePaths(int m, int n) {vector<vector<int>> dp(m, vector<int>(n, 0));for (int i = 0; i < m; i++) dp[i][0] = 1;for (int j = 0; j < n; j++) dp[0][j] = 1;for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m - 1][n - 1];}
};63、不同路径||
力扣题目链接
题意:
只是多了一个障碍物,网格中的障碍物和空位置分别用 1 和 0 来表示
具体实现跟62题区别不大,只是要处理一下障碍:
首先是每次用递推公式前判断是否有障碍:
if (obstacleGrid[i][j] == 0) { // 当(i, j)没有障碍的时候,再推导dp[i][j]dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
初始化也有不同:
vector<vector<int>> dp(m, vector<int>(n, 0));
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;代码:
优化版看不懂o(╥﹏╥)o太菜了......
class Solution {
public:int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {int m = obstacleGrid.size();int n = obstacleGrid[0].size();if (obstacleGrid[m - 1][n - 1] == 1 || obstacleGrid[0][0] == 1) //如果在起点或终点出现了障碍,直接返回0return 0;vector<vector<int>> dp(m, vector<int>(n, 0));for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) dp[i][0] = 1;for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) dp[0][j] = 1;for (int i = 1; i < m; i++) {for (int j = 1; j < n; j++) {if (obstacleGrid[i][j] == 1) continue;dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m - 1][n - 1];}
};343、整数拆分
力扣题目链接
题意:
给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。
返回 你可以获得的最大乘积 。
2 <= n <= 58
五步曲:
1.确定dp数组(dp table)以及下标的含义
dp[i]:分拆数字i,可以得到的最大乘积为dp[i]。
2.确定递推公式
可以想 dp[i]最大乘积是怎么得到的呢?
其实可以从1遍历j,然后有两种渠道得到dp[i].
一个是j * (i - j) 直接相乘。
一个是j * dp[i - j],相当于是拆分(i - j)
为何不拆分j?
j是从1开始遍历,拆分j的情况,在遍历j的过程中其实都计算过了。那么从1遍历j,比较(i - j) * j和dp[i - j] * j 取最大的。递推公式:dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));
其实还是不好理解(可能我太菜了,看了好久都不太能理解),我是这么想滴:
首先外层循环i,就是每个数字,跟以前题目一样,因为要从小到大排,其次是内层循环,相当于是要拆分一个数字,首先不知道拆成几个,其次不知道拆成什么,那就用一个循环,假设每个j都是确定的了,那剩下的数字是一个或者多个,换句话说,剩下那个未知的数字拆还是不拆,就像01背包的选还是不选:
for (int i = 3; i <= n ; i++) {for (int j = 1; j <= i / 2; j++) {dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));}
}i/2的来源:因为拆分一个数n 使之乘积最大,那么一定是拆分成m个近似相同的子数相乘才是最大的。
3.初始化:dp[2] = 1
4.确定遍历顺序
dp[i] 是依靠 dp[i - j]的状态,所以遍历i一定是从前向后遍历,先有dp[i - j]再有dp[i]。
5.举例推导dp数组√
code
class Solution {
public:int integerBreak(int n) {vector<int> dp(n + 1);dp[2] = 1;for (int i = 3; i <= n ; i++) {for (int j = 1; j <= i / 2; j++) {dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));}}return dp[n];}
};96、不同的二叉搜索树
力扣题目链接
题意:
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
1 <= n <= 19
五步曲:
首先是分析思路:
dp[3],就是 元素1为头结点搜索树的数量 + 元素2为头结点搜索树的数量 + 元素3为头结点搜索树的数量
元素1为头结点搜索树的数量 = 右子树有2个元素的搜索树数量 * 左子树有0个元素的搜索树数量
元素2为头结点搜索树的数量 = 右子树有1个元素的搜索树数量 * 左子树有1个元素的搜索树数量
元素3为头结点搜索树的数量 = 右子树有0个元素的搜索树数量 * 左子树有2个元素的搜索树数量
1.确定dp数组(dp table)以及下标的含义
dp[i] : 1到i为节点组成的二叉搜索树的个数为dp[i]。
2.在上面的分析中,其实已经看出其递推关系, dp[i] += dp[以j为头结点左子树节点数量] * dp[以j为头结点右子树节点数量]
j相当于是头结点的元素,从1遍历到i为止。
所以递推公式:dp[i] += dp[j - 1] * dp[i - j]; ,j-1 为j为头结点左子树节点数量,i-j 为以j为头结点右子树节点数量
3.初始化:dp[0] = 1
4.首先一定是遍历节点数,从递归公式:dp[i] += dp[j - 1] * dp[i - j]可以看出,节点数为i的状态是依靠 i之前节点数的状态。
那么遍历i里面每一个数作为头结点的状态,用j来遍历。
代码如下:
for (int i = 1; i <= n; i++) {for (int j = 1; j <= i; j++) {dp[i] += dp[j - 1] * dp[i - j];}
}5.举例over√
code
class Solution {
public:int numTrees(int n) {vector<int> dp(n + 1);dp[0] = 1;for (int i = 1; i <= n; i++) {for (int j = 1; j <= i; j++) {dp[i] += dp[j - 1] * dp[i - j];}}return dp[n];}
};好久没有更新了,实在是小学期太忙啦!
相关文章:
基础题目)
代码随想录算法训练营DAY09之动态规划(一)基础题目
理论基础: 如果某一问题有很多重叠子问题,使用动态规划是最有效的。 动态规划中每一个状态一定是由上一个状态推导出来的,这一点就区分于贪心,贪心没有状态推导,而是从局部直接选最优的。 例子: 例如&a…...
线性系统分析
一、定义 (1)叠加性 若 且 则称该系统具有叠加性。 叠加性:系统的一个输入不影响系统对其他输入的响应。 (2)均匀性 若 对任意常数a下式都成立 则称该系统具有均匀性。 均匀性:系统能够保持对输入信号的缩放因子不变。 (3)线性系统 若一个系统同时具有叠加性和…...

Ubuntu 20.04 部署 NET8 Web - Systemd 的方式 达到外网访问的目的
1.Ubuntu服务器环境安装 1.1 增加微软包安装源 wget https://packages.microsoft.com/config/ubuntu/22.04/packages-microsoft-prod.deb -O packages-microsoft-prod.deb sudo dpkg -i packages-microsoft-prod.deb1.2 Install the .NET SDK # 更新本地软件包列表。原理&am…...
:使用ExecutorService、ThreadPoolExecutor等线程池管理并发任务以及底层实现原理)
线程池(ThreadPool):使用ExecutorService、ThreadPoolExecutor等线程池管理并发任务以及底层实现原理
线程池(ThreadPool)是一种通过预先创建和维护一组线程的机制,用来高效管理并发任务。线程池不仅能减少创建和销毁线程的开销,还能更好地控制并发任务的执行。Java 中提供了多种方式来管理线程池,其中包括 ExecutorServ…...

人力资源数据集分析(二)_随机森林与逻辑回归
数据入口:人力资源分析数据集 - Heywhale.com 数据说明 字段说明EmpID唯一的员工IDAge年龄AgeGroup年龄组Attrition是否离职BusinessTravel出差:很少、频繁、不出差DailyRate日薪Department任职部门:研发部门、销售部门、人力资源部门Dista…...

【30天玩转python】数据库操作
数据库操作 数据库是应用程序中用于存储和管理数据的核心组件。Python 提供了多种与数据库交互的方式,支持不同类型的数据库,包括关系型数据库(如 MySQL、PostgreSQL)和 NoSQL 数据库(如 MongoDB)。在这篇…...

PTT:Point Tree Transformer for Point Cloud Registration 论文解读
目录 一、导言 二、相关工作 1、基于Transformer的点云配准 2、针对点云的局部注意力 三、PTT 1、KPconv提取特征 2、Tree Transformer Encoder 3、Decoder 4、估计姿态 5、损失函数 四、实验 1、对比不同Backbone 2、运行时间对比 3、对比不同PTT方法下RR指标的…...

C++速通LeetCode中等第7题-和为K的子数组(巧用前缀和)
巧用哈希表与前缀和,前缀和差为k的两个序号之间的数组就是满足条件的子数组,用哈希表来存放每个序号的前缀和。 前缀和就是头元素到当前序号子数组元素的和 class Solution { public:int subarraySum(vector<int>& nums, int k) {unordered_…...

【读书笔记-《30天自制操作系统》-23】Day24
本篇内容依然比较简单,主要是优化窗口功能以及开发定时器应用程序。首先是优化窗口的切换功能,实现通过键盘和鼠标切换窗口,然后是实现通过鼠标关闭窗口。接着实现不同窗口输入状态的切换,最后是实现定时器的API与应用程序。 1.…...
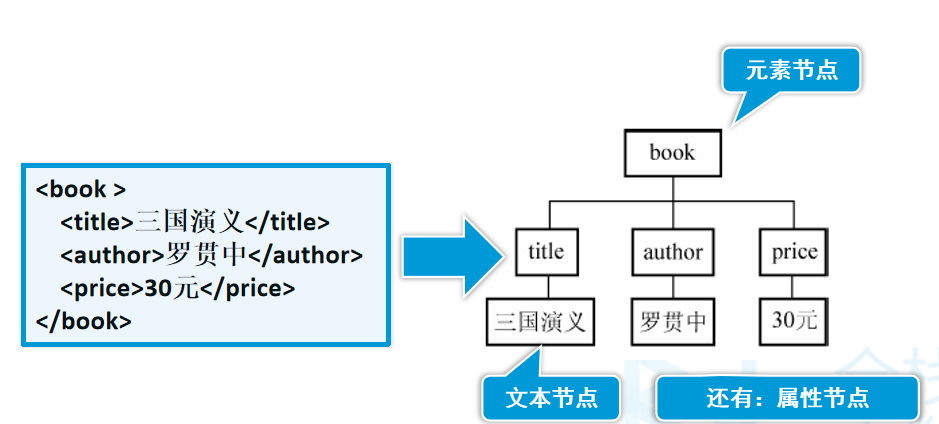
XML:DOM4j解析XML
XML简介: 什么是XML:XML 是独立于软件和硬件的信息传输工具。 XML 的设计宗旨是传输数据,而不是显示数据。XML 标签没有被预定义。您需要自行定义标签。XML不会做任何事情,XML被设计用来结构化、存储以及传输信息。 XML可以发明…...

15.5 创建监控控制平面的service
本节重点介绍 : k8s中service的作用和类型创建k8s控制平面的service 给prometheus采集用, 类型clusterIp kube-schedulerkube-controller-managerkube-etcd service的作用 Kubernetes Service定义了这样一种抽象: Service是一种可以访问 Pod逻辑分组…...

【Docker Nexus3】maven 私库
1.部署环境 window 11 x64Docker Desktop 4.34.1 (166053) Docker Engine v27.2.0 1.1.Docker 镜像源 1.1.1.Docker Engine 配置 {"builder": {"features": {"buildkit": true},"gc": {"defaultKeepStorage": "32…...
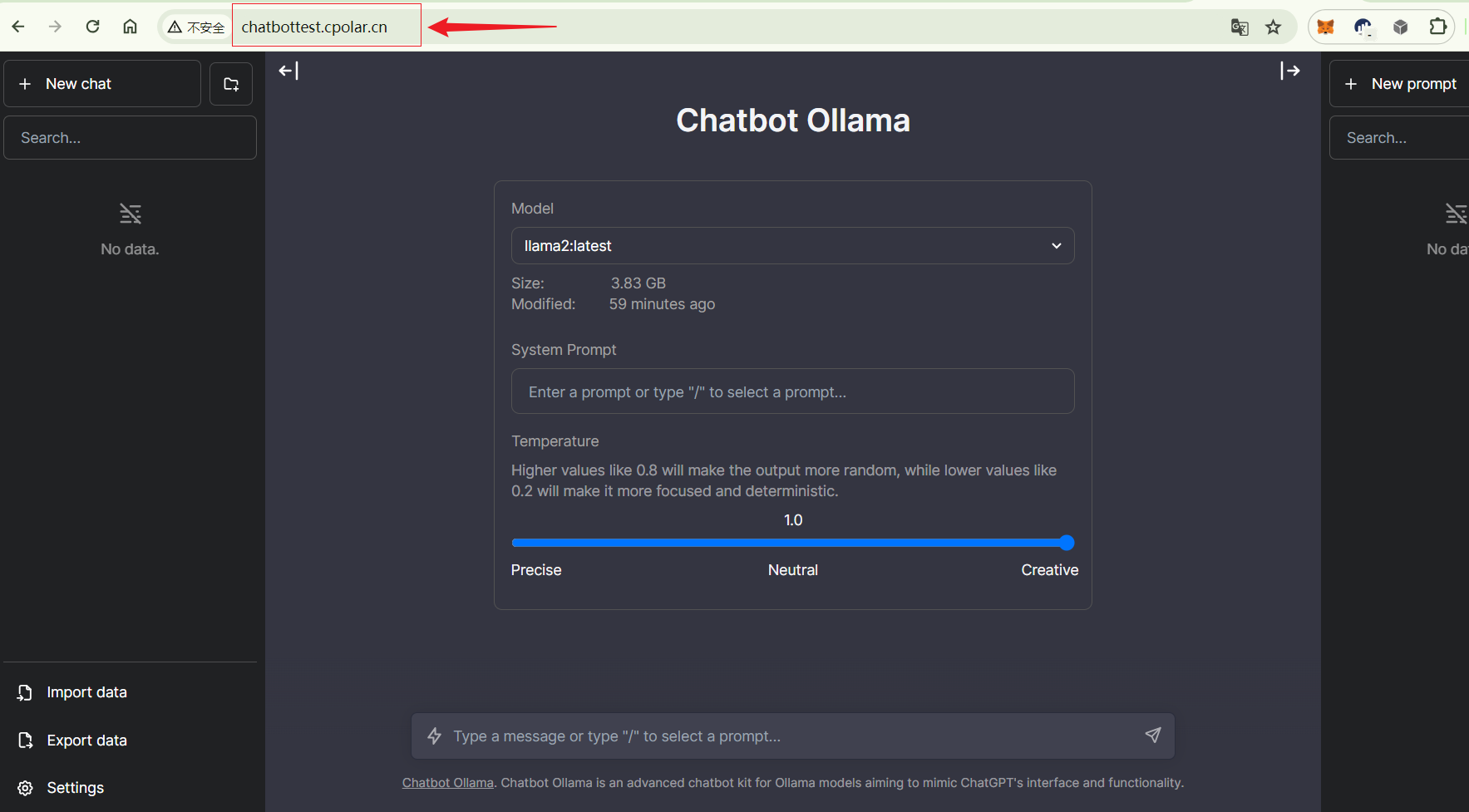
Docker本地部署Chatbot Ollama搭建AI聊天机器人并实现远程交互
文章目录 前言1. 拉取相关的Docker镜像2. 运行Ollama 镜像3. 运行Chatbot Ollama镜像4. 本地访问5. 群晖安装Cpolar6. 配置公网地址7. 公网访问8. 固定公网地址 前言 本文主要分享如何在群晖NAS本地部署并运行一个基于大语言模型Llama 2的个人本地聊天机器人并结合内网穿透工具…...

MySQL:用户管理
添加用户 create user usernamelocalhost identified by user_password;删除用户 drop user usernamelocalhost;查看所有用户 输入格式 select user,host from mysql.user; 输出 mysql> select user,host from mysql.user; ----------------------------- | user …...

论文《Mixture of Weak Strong Experts on Graphs》笔记
【Mowst 2024 ICLR】论文提出了一种新的图神经网络架构,称为Mixture of weak and strong experts(Mowst),通过将轻量级的多层感知机(MLP)作为弱专家和现成的GNN作为强专家相结合,以处理图中的节…...

【诉讼流程-健身房-违约-私教课-诉讼书提交流程-民事诉讼-自我学习-铺平通往法律的阶梯-讲解(3)】
【诉讼流程-健身房-违约-私教课-诉讼书提交流程-民事诉讼-自我学习-铺平通往法律的阶梯-讲解(3)】 1、前言说明2、流程说明3、现场提交(线下)4、网上提交1-起诉书样例2-起诉书编写(1)原告信息:&…...

数据结构(Day14)
一、学习内容 结构体 概念 引入:定义整数赋值为10 int a10; 定义小数赋值为3.14 float b3.14; 定义5个整数并赋值 int arr[5] {1 , 2 , 3 , 4 ,5}; 定义一个学生并赋值学号姓名成绩 定义一个雪糕并赋值名称产地单价 问题:没有学生、雪糕 数据类型 解决&…...

Paragon NTFS for Mac和Tuxera NTFS for Mac,那么两种工具有什么区别呢?
我们在使用Mac系统读取U盘的过程中往往会遇到一个问题,那就是U盘插进电脑无法显示,或者只能读取不能编辑。出现这种情况的原因就一般是格式错误。 很多小伙伴在解决这种问题的时候会选择使用U盘读写工具,那么哪一种读写工具比较好呢…...

HashTable结构体数组实现
写了个哈希表,底层逻辑基于结构体数组,核心结构:HashNode,结构外壳:HashTable_R,冲突处理以后会加的(QwQ)~ 目前代码: #ifndef PYIC_X #define PYIC_Xunsigned int PYIC_Hash(unsigned int Val, unsigned int Mov) {unsigned int Ht[4] { …...

Python 管理 AWS ElastiCache 告警
在 AWS 环境中,监控和管理 ElastiCache 集群的性能是至关重要的。本文将介绍如何使用 Python 和 AWS SDK (boto3) 来自动创建和删除 ElastiCache 集群的 CloudWatch 告警。我们将分两部分来讨论:创建告警和删除告警。 第一部分:创建 ElastiCache 告警 首先,让我们看看如何…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

es6+和css3新增的特性有哪些
一:ECMAScript 新特性(ES6) ES6 (2015) - 革命性更新 1,记住的方法,从一个方法里面用到了哪些技术 1,let /const块级作用域声明2,**默认参数**:函数参数可以设置默认值。3&#x…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...
