VCNet论文阅读笔记

VCNet论文阅读笔记

0、基本信息

信息	细节
英文题目	VCNet and Functional Targeted Regularization For Learning Causal Effects of Continuous Treatments
翻译	VCNet和功能目标正则化用于学习连续处理的因果效应
单位	芝加哥大学
年份	2021
论文链接	[2103.07861] VCNet和功能定向正则化用于学习连续处理的因果效应 (arxiv.org)
代码链接	https://github.com/lushleaf/varying-coefficient-net-with-functional-tr
发表会议	ICLR 2021 Conference Program Chairs

1、摘要

背景：因果推断（casual inference）在智能营销、药物治疗、决策上有广泛的应用，比如优惠券对用户购买意愿的影响、药品多大程度改善或治愈疾病、某项政策提高多少就业率等。（即，预估一种干预因素（treatment）对结果（outcome）的影响（treatment effect）），本文的目标问题就是获得ADRF曲线（平均剂量反应曲线）：x轴是药物浓度（treatment），y轴是患者效果（outcome）。

存在问题：

• 大多数uplift相关的论文都是关于binary treatment的因果效应估计，然而现实生活中，我们却经常遇到连续treatment (continues treatment)的情况。比如电商发放优惠券的满减金额是连续的，医生给病人开药的剂量是连续。那么我们应该如何对continues treatment对情况进行因果效应估计呢？

• 以前解决连续treatment的方法是将连续treatment分成多个blocks，使用不同的head处理不同的block，但是这样获得的outcome是不连续的（对应下图的Drnet曲线）。

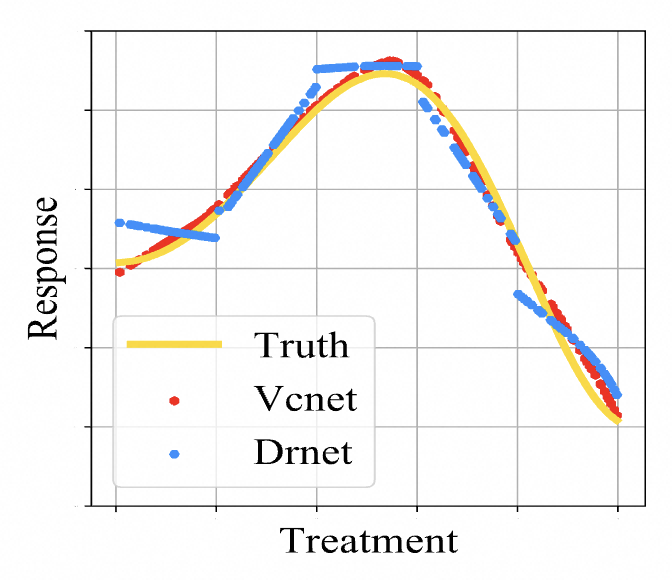
• 神经网络处理这个问题大多是，神经网络第一层是$(t,x)$，最后一层是$y$，这样做会存在treatment可能会在高维度表征中丢失的问题，以前的处理方法是将$t$，加到每个隐藏层上，但是这样做让预测更加的不连续。

文章贡献：

• 提出一个可变系数神经网络VCNet能处理连续干预的网络结构

• 推广了目标正则化，以获得整个ADRF曲线的双重鲁棒估计。

2、问题陈述和建模

iid 样本$\{(y\_i,\mathbf{x}\_i,t\_i)\}\_{i=1}^n$，其中X是协变量向量，T是连续treatment[0,1]，Y是结果

💎目标就是求平均剂量反应函数：

$\psi (t)=\mathbb{E}(Y\mid \text{do}(T=t))$

这里的 do 操作符表示“干预”或“人为设置”处理变量 𝑇 为 𝑡。这意味着我们要考虑的是，如果我们强制将处理设置为 𝑡，在这种情况下 𝑌的期望值。

患者	年龄 X	治疗水平 T	结果 Y
1	30	0.5	2
2	30	0.5	3
3	50	0.5	4
4	80	0.5	1

$\psi (0.5)=\mathbb{E}(Y\mid \text{do}(T=0.5))$

但在实际应用中，我们通常不能直接进行干预实验，我们只能观察到变量间的关系。在观察性数据中，我们常常用条件期望来替代这个干预性期望。我们需要将这个理论性的期望转换为可实际计算的形式。

$\psi (t)=\mathbb{E}(Y\mid \text{do}(T=t))=\mathbb{E}(\mathbb{E}(Y|X,T=t))$

$\psi (0.5)=\mathbb{E}(Y\mid \text{do}(T=0.5))=\mathbb{E}(\mathbb{E}(Y|X,T=0.5))$

$\mathbb{E}(Y|30,T=0.5)=(2+3)/2=2.5$

$\mathbb{E}(Y|50,T=0.5)=4$

$\mathbb{E}(Y|80,T=0.5)=1$

$\psi (0.5)=\mathbb{E}(\mathbb{E}(Y|X,T=0.5))=\mathbb{E}(\mathbb{E}(Y|30,T=0.5)+\mathbb{E}(Y|50,T=0.5)+\mathbb{E}(Y|80,T=0.5))$

$\psi (0.5)=$$(2.5+4+1)/3=2.42$

但是这里面存在一个问题：年长的患者可能更容易在同一治疗水平下有不同的结果（X存在混杂因素）。

解决方案：

提出一个广义倾向性得分的概念

$\mathbb{E}(\mathbb{E}(Y|X,T=t))$需要结合所有与 𝑋 相关的信息来进行计算。然而，当你面对的是复杂的数据，有时通过所有的 𝑋 来进行估计会引入噪声或混杂因素。

使用$\pi (t|x)$代表患者接受treatment的概率（$P(t|x)$）

倾向评分提供了一种将多维数据（特征 𝑋）映射到一维（治疗概率）的方法。这一映射使得我们能够更有效地建模和学习潜在的因果关系。

$\psi (t)=\mathbb{E}(Y\mid \text{do}(T=t))=\mathbb{E}(\mathbb{E}(Y|X,T=t))=\mathbb{E}(\mathbb{E}(Y|\pi (t|x),T=t))$

$\pi (0.5|30)=0.4$

$\pi (0.5|50)=0.3$

$\pi (0.5|80)=0.3$

$\psi (0.5)=\mathbb{E}(\mathbb{E}(Y|\pi (t|x),T=t))=(2.5\ast 0.4+4\ast 0.3+1\ast 0.3)/1=2.5$

通过这个过程，我们减少了由 𝑋引入的潜在偏倚，使得结果 𝑌 更好地反映了治疗的真实效果。

3、VCNet模型原理

3.1 基本结构

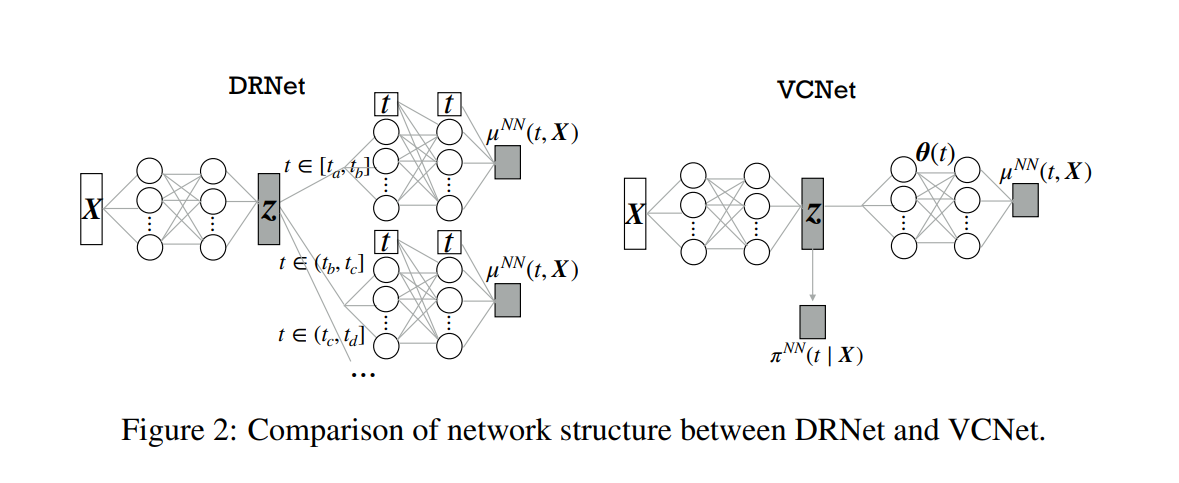
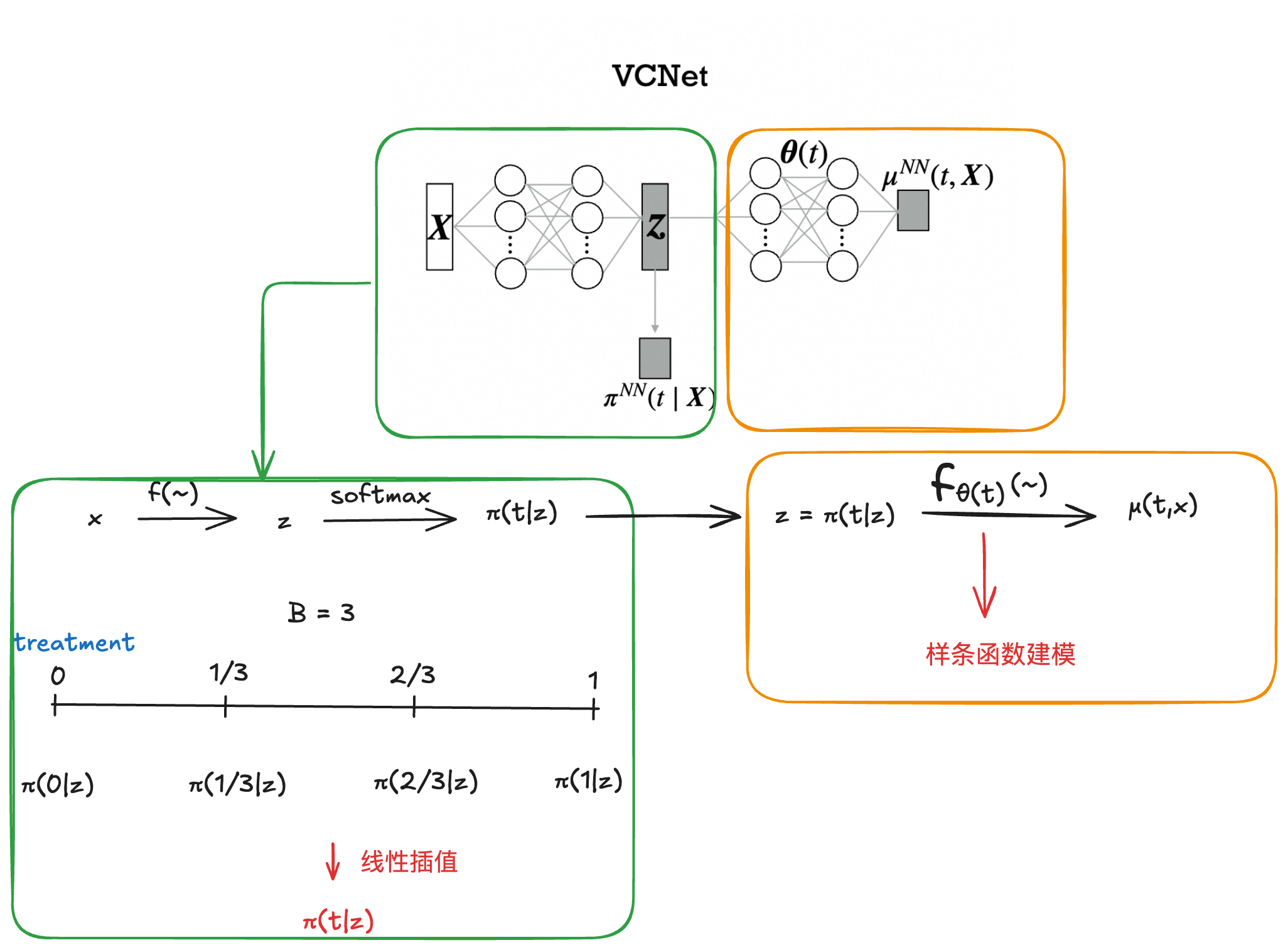
先使用简单的神经网络估计$\pi (t|x)$，之后使用VCNet得到预测结果

3.1 𝜋(𝑡|𝑋)估计

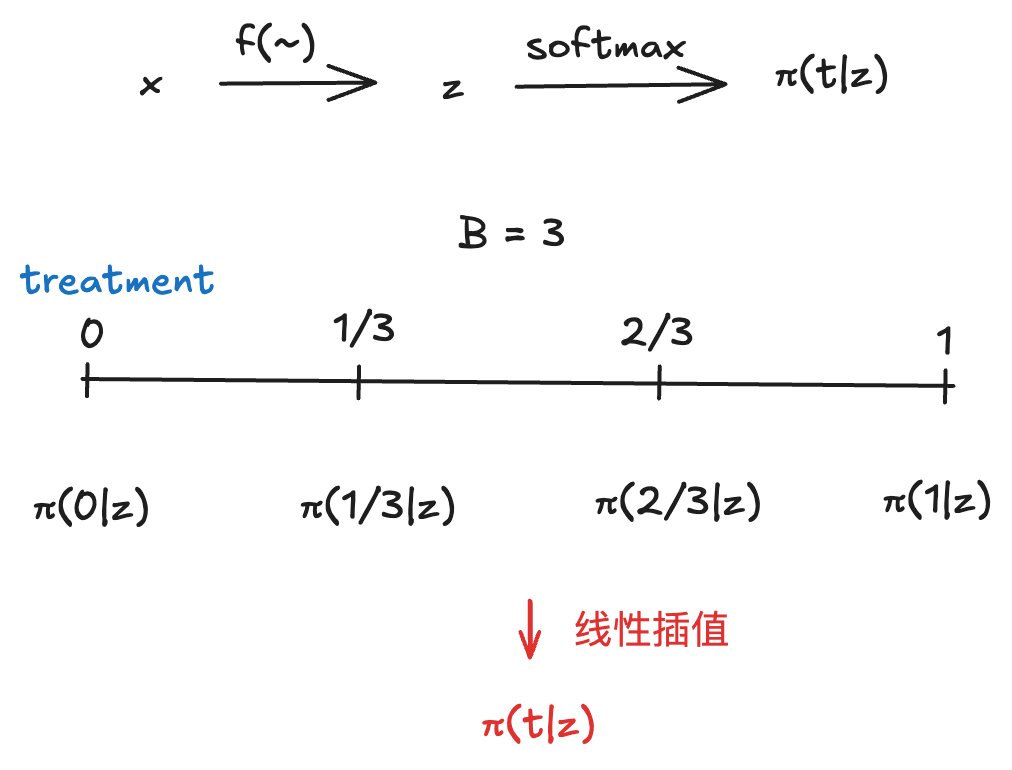
由于本文所提到的treatment是连续的，因此本文将treatment分成了B个grid区间，通过softmax转化成一个多分类问题，再通过差值估计得到最后的估计结果。

$\pi \_{grid}^{NN}(x)=softmax(wz)$

${\pi }^{NN}(t|x)=\pi \_{grid}^{t\_1,NN}(x)+B(\pi \_{grid}^{t\_2,NN}(x)-\pi \_{grid}^{t\_1,NN}(x))(t-t\_1)$

3.2 VCNet变系数估计

那如何得到变系数？VCNet中采用样条估计得到 𝜃(𝑡)，样条通过对间断点处的导数进行约束，可以实现间断点处的连续性。

一些简单的数学知识可以参考：码农小哥：一文读懂三次样条、曲线连续

假设$\theta \_i(t)=\sum \_{l=1}^{L}a\_i,l\varphi \_l^{NN}(t)$KaTeX parse error: Undefined control sequence: \[ at position 11: \theta(t)=\̲[̲\theta\_{1}(t),…， 𝑑𝜃(𝑡) 是 𝜃(𝑡) 的维度。

则

其中，$\left\{\varphi \_l^{NN}(t)\right\}\_{l=1}^L$为样条基， 𝑎𝑖,𝑙 为系数。则我们有

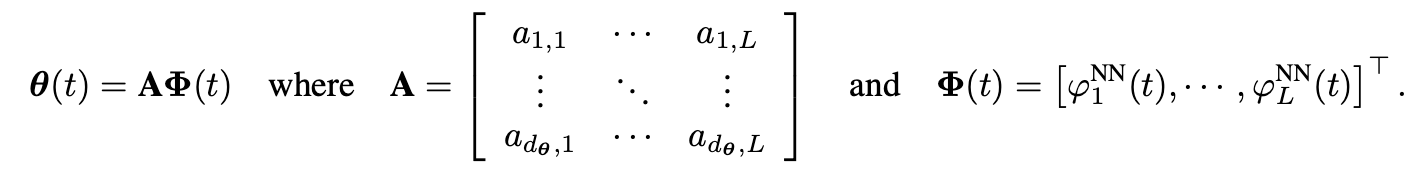
这里样条基的形式可以任意选择，假设以DRNet的多头形式估计变系数，DRNet其实也是VCNet的一个特例。

3.3 损失函数

同时优化π和μ

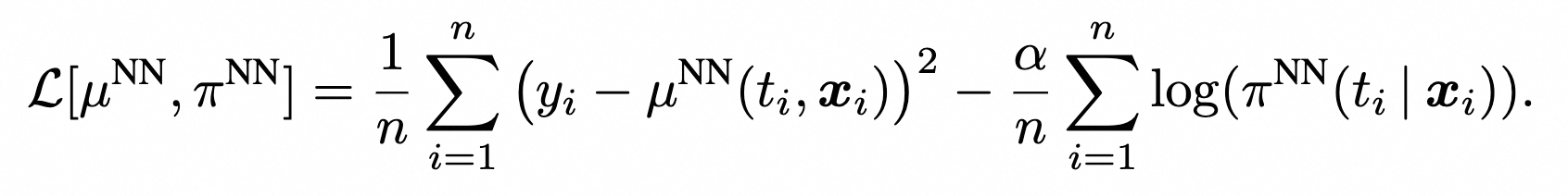
得到最优解

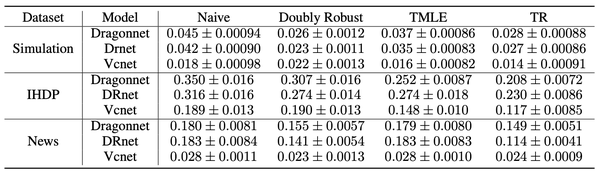
4、结果

从论文实验效果上看，VCNet对连续treatment的估计效果确实挺好的，同时加上DR也能很好的提升效果。

参考

• 连续干预下的深度因果推断 – VCNet解读 - 知乎 (zhihu.com)

• 因果推断笔记 | 连续型treatment因果效应估计之DRNet&VCNet - 知乎 (zhihu.com)