当前位置： 首页 > news >正文

Sublime text3怎么关闭提示更新

news 2026/2/9 11:34:46

问题 sublime text 3有新版本后,会不停地在每次启动后弹窗提示更新版本

第一步

软件安装之前，切记是软件安装之前！！！需要在hosts中添加以下内容(屏蔽官网联网检测)：hosts的位置一般在C:\Windows\System32\drivers\etc下，找到hosts文件后鼠标右键用记事本打开，在最后一行输入如下内容：  127.0.0.1    license.sublimehq.com 然后关闭，保存即可(如果提示无法保存，可鼠标选中hosts文件，右键属性->安全->;高级->点击所有者：SYSTEM 后面的更改->高级->立即查找->在下拉菜单中找到"本地账户"->确定->确定->应用->出现弹窗，点确定->确定->编辑->选中组或用户名当中的"Users(DESKTOP-XXXXX\users)"->勾选Users的权限下的：允许 完全控制->点应用->确定即可修改hosts文件了。这番操作可以说是一劳永逸，因为现在你可以完全控制你的计算机了，之前所有控制权是SYSTEM)   

第二步

点击菜单栏“Preferences”=> "Settings" 进入个人参数设置页面；修改右边的User Settings,添加一行:

 

"update_check": false,

设置完成后，重启软件就可以了.

相关文章：

Sublime text3怎么关闭提示更新

问题 sublime text 3有新版本后,会不停地在每次启动后弹窗提示更新版本 第一步 软件安装之前，切记是软件安装之前！！！需要在hosts中添加以下内容(屏蔽官网联网检测)：hosts的位置一般在C:\Windows\System32\drivers\etc…...

编程日记 2024/9/21 15:36:06

生成式语言模型技术栈

生成式语言模型的最新技术栈正在快速发展，尤其是随着大规模预训练模型（LLMs）和生成式AI的应用不断扩展。以下是当今最前沿的生成式语言模型技术栈，涵盖从模型开发到优化、推理和部署的各个环节。 1. 基础模型开发 基础模型开发包…...

编程日记 2024/9/21 15:35:05

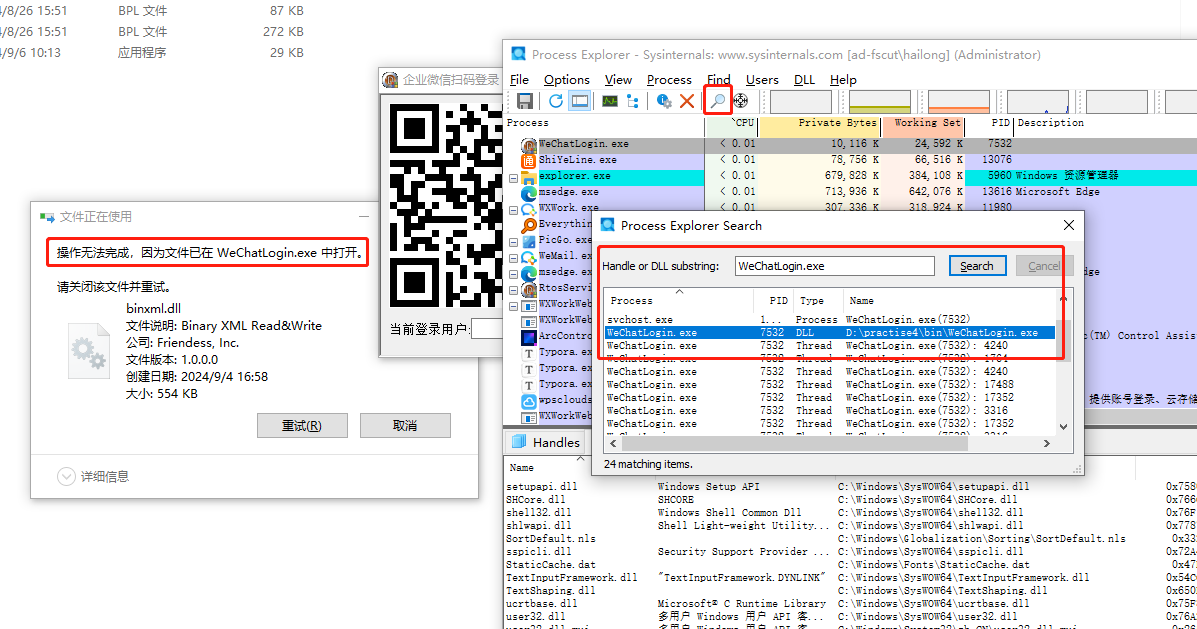
进程分析工具Process Explorer使用

进程分析工具Process Explorer使用 Process Explorer让使用者能了解看不到的在后台执行的处理程序，能显示目前已经载入哪些模块，分别是正在被哪些程序使用着，还可显示这些程序所调用的DLL进程，以及他们所打开的句柄。Process Expl…...

编程日记 2024/9/21 15:34:04

vue 中如何实现鼠标拖动出发滚动条的跟随移动？

使用场景 在做弹窗、表单或 tab 切换需求的时候，有时候因为内容过长会导致出现滚动条，但是只能拖动滚动条时会导致操作不便，我们会希望实现通过拖动内容区实现滚动条的滑动。这样操作就会简单多了。 实现思路 如果要实现鼠标辅助触发滚动条…...

编程日记 2024/9/21 15:33:03

【Java EE】文件IO

Author：MTingle major:人工智能 --------------------------------------- Build your hopes like a tower! 目录 一、文件是什么？ 二、针对文件系统操作的API 1.文件路径，文件名，文件是否存在 2. 创建文件 3.删除文件&#…...

编程日记 2024/9/21 15:32:01

使用 React、Material-UI、Spring、MySQL、MyBatis 以及高德 API 模拟实时位置信息

要使用 React、Material-UI、Spring、MySQL、MyBatis 以及高德 API 模拟实时位置信息，你可以按以下步骤来实现： 目录 1. 前端 (React Material-UI) 2. 后端 (Spring Boot MyBatis MySQL) 3. 模拟实时位置数据 4. 前后端联调 1. 前端 (React Mat…...

编程日记 2024/9/21 15:31:00

UniApp一句话经验： px -＞ rpx动态转换和动态元素区域的获取

px->rpx转换 在多终端条件下，什么devicePixelRatio，upx2px都是不靠谱的，最直接的是这样： const { screenWidth } uni.getSystemInfoSync()const pixelUnit screenWidth / 750 // rpx->px比例基数 动态元素区域获取 多终…...

编程日记 2024/9/21 15:29:59

Python基于flask框架的智能停车场车位系统 数据可视化分析系统fyfc81

目录 技术栈和环境说明解决的思路具体实现截图系统设计python语言django框架介绍flask框架介绍性能/安全/负载方面可行性分析论证python-flask核心代码部分展示python-django核心代码部分展示技术路线操作可行性详细视频演示源码获取 技术栈和环境说明 结合用户的使用需求&…...

编程日记 2024/9/21 15:25:55

海外服务器哪个速度最快且性能稳定

海外服务器的速度与性能稳定性受多种因素影响，包括地理位置、网络架构、基础设施质量以及用户网络路径等。在众多选择中，几个特定地区的服务器因其卓越表现而备受推崇。 首先，美国硅谷(加利福尼亚州)与纽约的服务器以其技术领先、网络连接稳定…...

编程日记 2024/9/21 15:24:53

C/C++通过CLion2024进行Linux远程开发保姆级教学

目前来说，对Linux远程开发支持相对比较好的也就是Clion和VSCode了，这两个其实对于C和C语言开发都很友好，大可不必过于纠结使用那个，至于VS和QtCreator，前者太过重量级了，后者更是不用说，主要用于…...

编程日记 2024/9/21 15:19:47

工程师 - 如何安装Windows 终端

Windows 终端是一款适用于 Windows 的现代命令行应用程序，支持多个终端会话，包括 Command Prompt、PowerShell 和 Windows Subsystem for Linux (WSL)。它具有标签式界面、可定制的设置（如主题和按键绑定）、改进的文本渲染以及对 …...

编程日记 2024/9/21 15:18:46

UniApp 从Vue2升级为Vue3需要注意哪些方面

Vue官方已经发布了Vue3，Vue2不再维护，也在建议大家都迁移到Vue3，所以Vue2终会被淘汰。 那么UniApp 从Vue2升级为Vue3需要注意哪些方面： 1、main.js 下面请看创建应用实例Vue2与Vue3的不同： Vue2的写法：…...

编程日记 2024/9/21 15:16:43

前端面试CSS常见题目

1. CSS 选择器的优先级 (Specificity) 面试官通常会问你如何计算 CSS 选择器的优先级&#xff0c;这对于避免样式冲突、提高代码可维护性很重要。 优先级计算规则&#xff1a; !important 优先级最高。内联样式&#xff08;例如&#xff1a;<div style"color: red;&…...

编程日记 2024/9/21 15:13:39

408算法题leetcode--第10天

643. 子数组最大平均数 I 643. 子数组最大平均数 I思路&#xff1a;滑动窗口时间&#xff1a;O(n)&#xff1b;空间&#xff1a;O(1) class Solution { public:double findMaxAverage(vector<int>& nums, int k) {double ret 0, temp 0;size_t size nums.size()…...

编程日记 2024/9/21 15:12:38

13年计算机考研408-数据结构

解析&#xff1a; 这个降序链表不影响时间复杂度&#xff0c;因为是链表&#xff0c;所以你想要升序就使用头插法&#xff0c;你想要降序就使用尾插法。 然后我们来分析一下最坏的情况是什么样的。 因为m和n都是两个有序的升序序列。 如果刚好m的最大值小于n的最小值&#xff0…...

编程日记 2024/9/21 15:11:37

跨平台开发新视角：利用Android WebView实现Web内容的原生体验

在移动应用开发领域&#xff0c;跨平台解决方案一直是一个热门话题。开发者们不断寻求能够同时在iOS和Android平台上提供一致用户体验的方法。而Android的WebView组件&#xff0c;作为一个强大的工具&#xff0c;允许开发者在Android应用中嵌入Web内容&#xff0c;为用户提供接…...

编程日记 2024/9/21 15:08:33

Stable Diffusion 使用详解（11）--- 场景ICON制作

目录 背景 controlNet 整体描述 Canny Lineart Depth 实际使用 AI绘制需求 绘制过程 PS打底 场景模型选择 设置提示词及绘制参数 controlnet 设置 canny 边缘 depth 深度 lineart 线稿 效果 背景 这段时间不知道为啥小伙伴似乎喜欢制作很符合自己场景的ICON。…...

编程日记 2024/9/21 15:04:29

【Linux系统编程】第二十弹---进程优先级 命令行参数 环境变量

✨个人主页&#xff1a; 熬夜学编程的小林 &#x1f497;系列专栏&#xff1a; 【C语言详解】 【数据结构详解】【C详解】【Linux系统编程】 目录 1、进程优先级 2.1、什么是优先级 2.2、优先级的描述 2.3、优先级与权限的关系 2.4、为什么要有优先级 2.5、Linux优先级的…...

编程日记 2024/9/21 15:02:28

无人机之4G模块的主要功能和优势

一、增强图传 在无人机飞行过程中&#xff0c;传统的图传方式可能会受到信号遮挡或干扰的影响&#xff0c;导致图像传输不稳定甚至中断。而4G模块通过结合4G网络技术&#xff0c;能够在原有图传技术的基础上提供增强的图传功能。当传统图传信号不佳时&#xff0c;无人机可以自动…...

编程日记 2024/9/21 15:01:27

深度学习-03 Pytorch

损失函数是用来衡量模型预测结果与真实值之间的差异&#xff0c;并用来优化模型的指标。在机器学习和神经网络中&#xff0c;常用的损失函数包括均方误差&#xff08;Mean Squared Error&#xff0c;MSE&#xff09;、交叉熵&#xff08;Cross-Entropy&#xff09;等。 反向传播…...

编程日记 2024/9/21 14:56:22

深入理解JavaScript设计模式之单例模式

目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式&#xff08;Singleton Pattern&#…...

编程新知 2026/1/31 17:09:43

postgresql|数据库|只读用户的创建和删除（备忘）

CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

编程新知 2025/9/18 19:34:22

什么是Ansible Jinja2

理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具&#xff0c;可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板&#xff0c;允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板&#xff0c;并通…...

编程新知 2026/2/6 1:00:25

SiFli 52把Imagie图片，Font字体资源放在指定位置，编译成指定img.bin和font.bin的问题

分区配置 (ptab.json) img 属性介绍&#xff1a; img 属性指定分区存放的 image 名称&#xff0c;指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件&#xff0c;则以 proj_name:binary_name 格式指定文件名&#xff0c; proj_name 为工程 名&…...

编程新知 2026/1/23 10:51:19

【深度学习新浪潮】什么是credit assignment problem？

Credit Assignment Problem（信用分配问题） 是机器学习，尤其是强化学习（RL）中的核心挑战之一，指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中，智能体执行一系列动作后获得一个最终奖励，但每个动作对最终结果的贡献程度往往…...

编程新知 2026/1/30 14:23:04

加密通信 + 行为分析：运营商行业安全防御体系重构

在数字经济蓬勃发展的时代&#xff0c;运营商作为信息通信网络的核心枢纽&#xff0c;承载着海量用户数据与关键业务传输&#xff0c;其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级&#xff0c;传统安全防护体系逐渐暴露出局限性&a…...

编程新知 2025/9/9 18:03:51

聚六亚甲基单胍盐酸盐市场深度解析：现状、挑战与机遇

根据 QYResearch 发布的市场报告显示&#xff0c;全球市场规模预计在 2031 年达到 9848 万美元&#xff0c;2025 - 2031 年期间年复合增长率&#xff08;CAGR&#xff09;为 3.7%。在竞争格局上&#xff0c;市场集中度较高&#xff0c;2024 年全球前十强厂商占据约 74.0% 的市场…...

编程新知 2026/2/3 2:04:52

Tauri2学习笔记

教程地址&#xff1a;https://www.bilibili.com/video/BV1Ca411N7mF?spm_id_from333.788.player.switch&vd_source707ec8983cc32e6e065d5496a7f79ee6 官方指引&#xff1a;https://tauri.app/zh-cn/start/ 目前Tauri2的教程视频不多&#xff0c;我按照Tauri1的教程来学习&…...

编程新知 2026/2/4 20:00:27

深度解析云存储：概念、架构与应用实践

在数据爆炸式增长的时代&#xff0c;传统本地存储因容量限制、管理复杂等问题&#xff0c;已难以满足企业和个人的需求。云存储凭借灵活扩展、便捷访问等特性&#xff0c;成为数据存储领域的主流解决方案。从个人照片备份到企业核心数据管理&#xff0c;云存储正重塑数据存储与…...

编程新知 2025/10/30 6:08:18

【题解-洛谷】P10480 可达性统计

题目&#xff1a;P10480 可达性统计 题目描述 给定一张 N N N 个点 M M M 条边的有向无环图&#xff0c;分别统计从每个点出发能够到达的点的数量。 输入格式 第一行两个整数 N , M N,M N,M&#xff0c;接下来 M M M 行每行两个整数 x , y x,y x,y&#xff0c;表示从 …...

编程新知 2025/12/15 8:11:23