当前位置：首页 > news >正文

【数据结构】排序算法系列——快速排序（附源码+图解）

news 2026/2/4 12:22:35

快速排序

接下来我们将要介绍的是排序中最为重要的算法之一——快速排序。

快速排序（英语：Quicksort），又称分区交换排序（partition-exchange sort），最早由东尼·霍尔提出。快速排序通常明显比其他算法更快，因为它的内部循环可以在大部分的架构上很有效率地达成。我们直接来分析它的算法思想。

算法思想与图解

我们首先直接来看算法步骤，再分析其原理和目的

首先确定一个基准值，基准值一般选最左边或者最右边的
然后使用左右指针对数据和基准值进行大小比较
比基准值小的放左边，比基准值大的放右边，从而使得最终基准值的左边比其小，右边比其大
递归重复此步骤，注意基准值不能重复，直到完全有序

具体的动画分析可以看这：快速排序算法动画演示_哔哩哔哩_bilibili

我们首先来对基准值的选择进行分析：

通常我们都会选择最左边或者最右边的基准值，这是最不需要多想的选择方法；

但是往往我们需要考虑时间效率，这样选择的话，时间效率是怎样的呢？我们知道最左边和最右边的数有可能是整个数据组中最大或者最小的数，而一轮快速排序的最终目的就是使用基准值将数据分为比其大和比其小的两部分，那么如果记住基准值本身就是一个最值，排序完之后必定也只会在最前或者最后一个位置，这样就会进行浪费的比较，从而降低效率。

在这里插入图片描述

如果我们需要规避这种最坏的情况，我们可以使用随机基准值或者三数取中法。这样能够有效规避最坏情况的发生，但并非绝对事件。

//1.随机取基准值
//随机选基准值，从而可以有效减小最坏情况的概率 
int randindex = rand() % (right - left + 1) + left;
Swap(&a[randindex], &a[left]);//2，三数取中
int GetMid(int* a, int left, int right)
{int mid = (left + right) / 2;if (a[left] < a[mid])//左边和中间比较{if(a[mid]<a[right])return mid;else if (a[left] < a[right])return right;elsereturn left;}else//左边和中间比较{if (a[mid] > a[right])return mid;else if (a[left] > a[right])return right;elsereturn left;}
}

从基准值的选择我们其实也可以看出，实际上快速排序的核心思想就是使用基准值，将数据组分成两份。这也是它分区交换排序名字的由来。分析分区原理，只要一直不断地进行分区操作，那么最后每个数都可以成为一次基准值，也就可以达到每个数的左边都比其小，右边都比其大，那么整体来看就已经实现了完全有序。

C语言代码分析

霍尔快排

void QuickSort1(int* a, int left, int right)
{if (left >= right)return;//随机选基准值，从而可以有效减小最坏情况的概率 int randindex = rand() % (right - left + 1) + left;Swap(&a[randindex], &a[left]);int key = left;//选择最左边为基准值while (left < right){//右边找小的while (a[right] >= a[key])right--;//左边找大的while (a[left] <= a[key])left++;Swap(&a[left], &a[right]);}Swap(&a[key], &a[left]);//二叉树的递归方式QuickSort1(a, key, left - 1);//递归左边QuickSort1(a, left + 1, right);//递归右边
}
//霍尔单趟
int PartSort1(int* a, int left, int right)
{if (left >= right)return;//随机选基准值，从而可以有效减小最坏情况的概率 int randindex = rand() % (right - left + 1) + left;Swap(&a[randindex], &a[left]);int key = left;//选择最左边为基准值while (left < right){//右边找小的while (a[right] >= a[key])right--;//左边找大的while (a[left] <= a[key])left++;Swap(&a[left], &a[right]);}Swap(&a[key], &a[left]);return left;}

注意

二叉树思想

我们观察上述的代码，会发现我们的分区思想与[[二叉树]]的思想略有相似：将基准值看成根节点，那么它的左子树——也就是左边的部分绝对比其小；类似，右子树也绝对比其大（都反过来也可）——实际上霍尔当时就是根据[[二叉树]]的思想从而发明了这样一种排序的算法。

左右指针相遇的逻辑

初始化指针：
- 左指针从数组的起始位置开始向右移动，寻找一个大于基准值的元素。
- 右指针从数组的末尾开始向左移动，寻找一个小于基准值的元素。
移动指针：
- 左指针向右移动，直到找到一个大于等于基准值的元素。
- 右指针向左移动，直到找到一个小于等于基准值的元素。
指针相遇：
- 当左右指针相遇时，意味着左指针的位置是一个元素大于基准值的位置，而右指针已经通过其他元素找到了一个小于基准值的元素。此时可以认为，左指针的位置应该是大于或等于基准值的（可能因为左指针已经停止在一个比基准值小的元素上），而右指针的位置则是小于或等于基准值的。

为什么相遇节点永远小于基准值

在理想的情况下，通过上述移动，左右指针不会交叉的情况下，最终会在一个位置相遇，这个位置可能就是基准值的位置，也可能比基准值小。而这个位置的元素比基准值小的原因是基于以下几点：

分区约束：
- 根据右边先走，左边再走的顺序，左右指针最终需要相遇前会有以下两种情况：
  
  1.右指针找到小的，左指针没有找到大的，那么此时继续移动二指针就会相遇。
  
  2,右指针没有找到小的，继续移动直到遇到了左指针，鉴于左指针本身就比基准值要小或者相等（才会停下），所以此时的相遇位置就可以是比基准值要小。
  
  无独有偶，当左边先走，右边再走时就有可能遇见比基准值大的相遇位置。
基准值的定义：
- 最终将会把基准值放在左右指针交会的位置的元素上。这个位置的特性就是：在其左边的都是小于基准值的元素，而在其右边的都是大于基准值的元素。

因此，尽管左右指针可能在不等于基准值的元素上相遇，实际上通过合并数据的方式能整理出期望的排序效果。因此，它并不意味着相遇位置的元素永远小于基准值，而是说在执行分区后，基准值应该放在那个位置以满足排序的条件。

算法优化

快速排序除了霍尔发明的最初的一种算法，实际上还有改进算法。

挖坑法

挖坑法的实质是不断变换坑位，这个坑位最终是用来存放基准值的位置。而在算法中我们将看到坑位始终是根据左右指针来进行定位的，因此当坑位要存放基准值也就是单趟结束的时候，左右指针会相遇在基准值的坑位。左右指针的移动也是根据同基准值的大小来决定的。

这个算法的好处是有助于我们更好地理解快排的本质，从而优化算法。

//挖坑法的实质就是不断变基准值的位置，直到找到基准值的位置
void QuickSort2(int* a, int left, int right)
{if (left >= right)return;int begin = left, end = right;//三数取中int mid = GetMid(a, left, right);if (left != mid)Swap(&a[left], &a[mid]);int key = a[left];int hole = left;//挖坑位置while (left < right){//右边找小的while (a[right] >= a[key])right--;a[hole] = a[right];//填坑hole = right;//左边找大的while (a[left] <= a[key])left++;a[hole] = a[left];//填坑hole = left;Swap(&a[left], &a[right]);}Swap(&a[key], &a[left]);//二叉树的递归方式QuickSort1(a, key, left - 1);//递归左边QuickSort1(a, left + 1, right);//递归右边
}//挖坑单趟
void PartSort2(int* a, int left, int right)
{//三数取中int mid = GetMid(a, left, right);if (left != mid)Swap(&a[left], &a[mid]);int key = a[left];int hole = left;//挖坑位置while (left < right){//右边找小的while (a[right] >= a[key])right--;a[hole] = a[right];//填坑hole = right;//左边找大的while (a[left] <= a[key])left++;a[hole] = a[left];//填坑hole = left;}a[hole] = key;return hole;
}

前后指针法

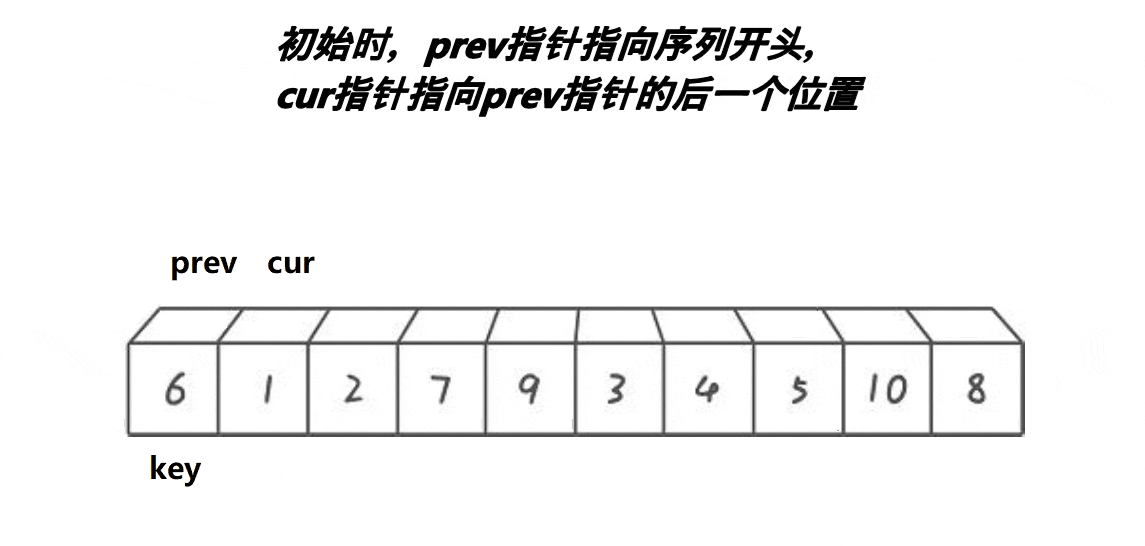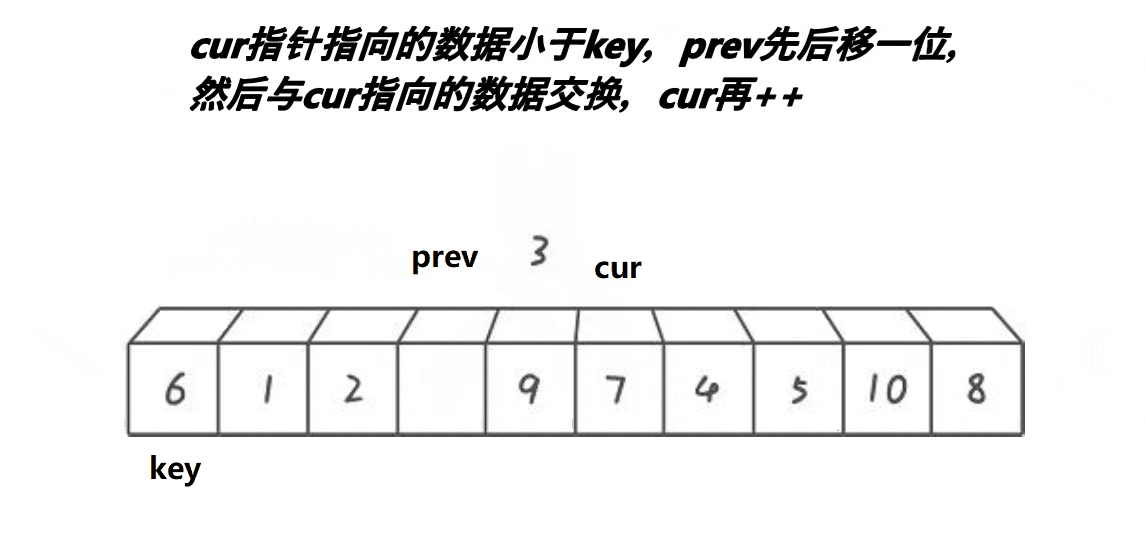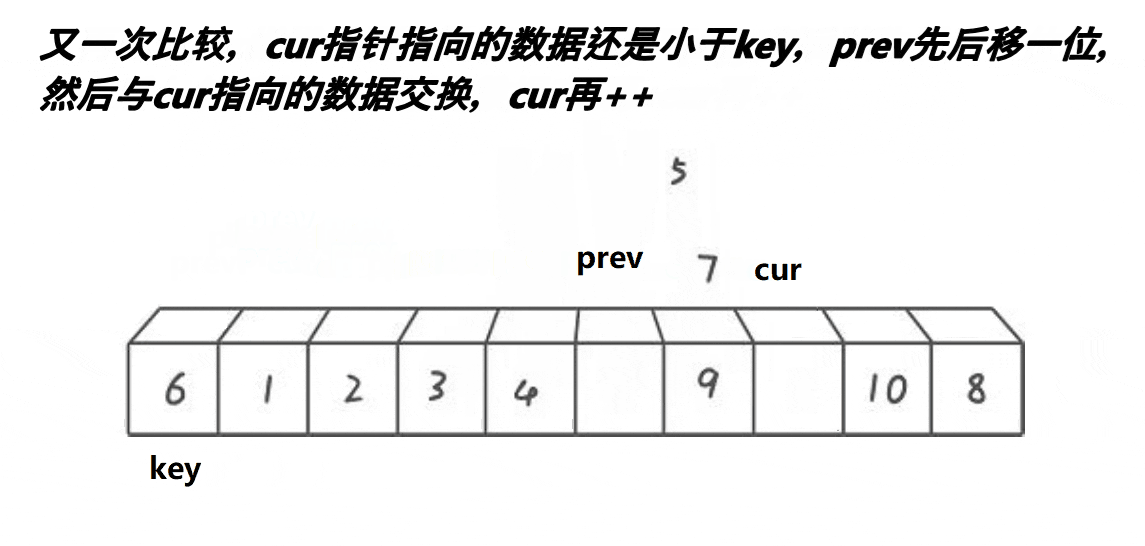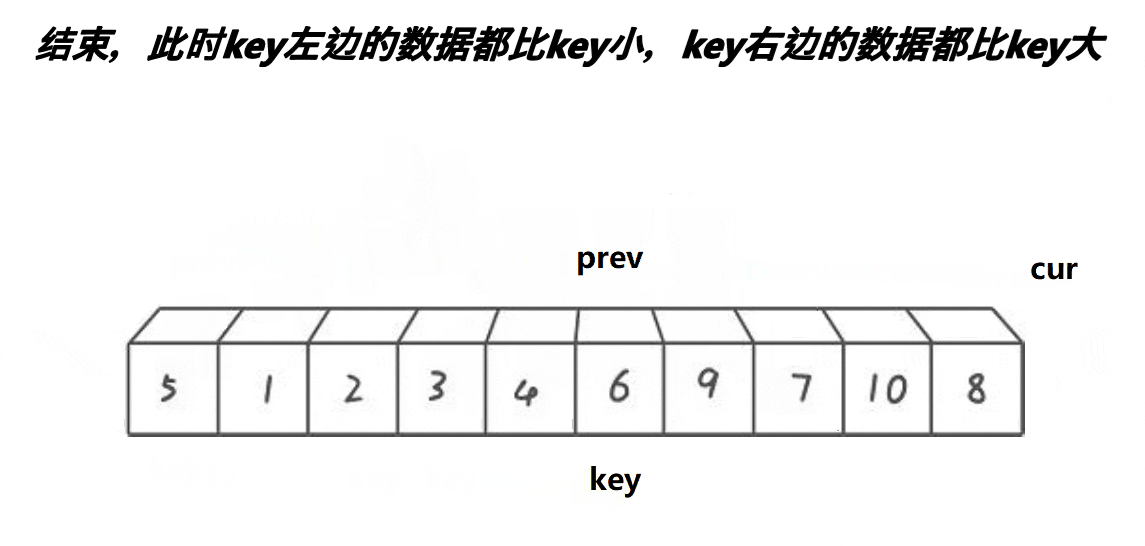
前后指针法使用cur和prev前后两个指针进行移动，规则如下：

A.cur找到比基准值小的值，prev++，再将cur与prev位置的值交换，cur++
B.cur找到比基准值大的值，cur++
当cur越界（识别完所有的数据）时，结束所有的移动，将基准值放入此时prev的位置。

我们分析，在这两种情况下，prev要么就是紧跟cur，两个指针一直依附着对方前进，要么就是中间间隔的数都比基准值要大；同时它也实现了快排的核心思想：比基准值大的放右边，比基准值小的放左边。

//第三种是前后指针法
//前后指针法的实质是通过比较后指针和基准值的大小，
//然后满足大小条件时进行前后指针交换
//交换的原则就是把小的放在前边，大的放在后边
void QuickSort3(int* a, int left, int right)
{int mid = GetMid(a, left, right);if (mid != left)Swap(&a[left], &a[mid]);int key = left;int prev = left;int cur = left + 1;while (cur <= right){if (a[cur] <a[key] && ++prev != cur){Swap(&a[cur], &a[prev]);}cur++;}Swap(&a[prev], &a[key]);key = prev;return key;}//前后指针单趟
int PartSort3(int* a, int left, int right)
{int mid = GetMid(a, left, right);if (mid != left)Swap(&a[left], &a[mid]);int key = left;int prev = left;int cur = left + 1;while (cur <= right){if (a[cur] < a[key] && ++prev != cur){Swap(&a[cur], &a[prev]);}cur++;}Swap(&a[prev], &a[key]);key = prev;return key;}

非递归快排

非递归版本主要通过显式栈来模拟递归调用栈。

使用非递归的原因：当数据过多的时候，递归算法就会跑不起来——递归需要建立栈帧，当建立了过多的栈帧就会出现栈溢出的情况。

初始化栈：创建一个栈来保存需要处理的数组区间。
入栈：将整个数组的左右边界（即数组的起始和结束索引）入栈。
循环处理：
1. 从栈顶弹出一对左右边界。
2. 使用这些边界对数组进行分区，找到分区的中间点（即分区点）。
3. 将分区点两侧的左右边界分别入栈，表示后续需要处理的子数组。
4. 如果某个子数组的元素数量少于等于1，则不需要入栈处理。
结束：当栈为空时，所有区间都已经处理完毕，排序完成。

//非递归实现快排
void QuickSortNoR(int* a, int left, int right)
{ST s;STInit(&s);STPush(&s, left);//先将左右边界入栈STPush(&s, right);while (STEmpty(&s)){//取出左右边界int begin = STTop(&s);STPop(&s);int end = STTop(&s);STPop(&s);//使用一次单趟的快排得到第一次的基准值int key = PartSort3(a, begin, end);//将基准值的左右边界入栈if (key + 1 < end){STPush(&s, end);STPush(&s, key + 1);}if (begin < key-1){STPush(&s, key-1);STPush(&s, begin);}}STDestroy(&s);
}

代码解析

S结构体：用来保存左右边界索引。
PartSort3函数：选择数组的最右边元素为基准元素，通过交换使得基准元素的左侧都是小于等于它的元素，右侧都是大于它的元素。返回值是基准元素的最终位置。

这个算法是利用栈模拟递归过程，适用于不能使用递归的环境或递归深度较大的情况。

时间复杂度

关于快速排序为什么是最好的排序算法之一，肯定与它优秀的时间效率扯不开关系。这里我们直接看维基对于其平均时间复杂度的分析：

在这里插入图片描述

可以看到，快速排序从根本上就能够良好的减少遇见最坏情况的概率，而它的最坏情况实际上也坏不到哪去，如此优秀的排序机制也为它奠定了基础和不可动摇的地位。

最坏情况：O(n²)

最好情况：O(n logn)

稳定性

鉴于快速排序会改变前后元素的相对位置，所以：不稳定