【多维动态规划】64. 最小路径和(面试真题+面试官调整后的题目)
64. 最小路径和
难度:中等
力扣地址:https://leetcode.cn/problems/minimum-path-sum/description/

1. 原题以及解法
1.1 题目
给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和为最小。
说明:每次只能 向下 或者 向右 移动一步。
示例 1:

输入:grid = [[1,3,1],[1,5,1],[4,2,1]]
输出:7
解释:因为路径 1→3→1→1→1 的总和最小。
示例 2:
输入:grid = [[1,2,3],[4,5,6]]
输出:12
提示:
- m == grid.length
- n == grid[i].length
- 1 <= m, n <= 200
- 0 <= grid[i][j] <= 200
1.2 分析过程
首先应当分析简单的情况:如下图所示,长度为 2 x 2 时的最小路径和过程

接着我们需要计算尺寸更大情况的最小路径。


分析结论
- 上图已经提到转移方程,即
dp[i][k] = min(dp[i-1][k], dp[i][k-1]) + grid[i][k]。但是需要注意这个公式的适用场景:i >= 1, k >= 1。 - 对于
i == 0以及k == 0的情况(第一行与第一列),通过累加的方式即可更新dp值。
1.3 解题代码
class Solution {
public:int minPathSum(vector<vector<int>>& grid) {int row = grid.size();int column = grid[0].size();vector<vector<int>> dp(row, vector<int>(column));dp[0][0] = grid[0][0];// 第一行每个点的最小路径for (int i = 1; i < column; i++) {dp[0][i] = grid[0][i] + dp[0][i - 1];}// 第一列每个点的最小路径for (int i = 1; i < row; i++) {dp[i][0] = grid[i][0] + dp[i - 1][0];}/** 对于 dp[i][k] 的计算规则为* dp[i][k] = min(dp[i - 1][k], dp[i][k - 1]) + grid[i][k]*/for (int i = 1; i < row; i++) {for (int k = 1; k < column; k++) {dp[i][k] = min(dp[i - 1][k], dp[i][k - 1]) + grid[i][k];}}return dp[row - 1][column - 1];}
};
2. 拓展(带条件的多维动态规划)
注:据可靠保熟消息,本题是一道面试题,面试官首先考察了与力扣第64题相同的,然后在这个基础上添加了这个条件,希望参与者手撕代码。
在这个题的基础上添加限制条件:存在一个或多个障碍物堵塞路径,如果题目中无路径则返回 -1。
如下是一个基于力扣第64题调整后的新题目:
2.1 拓展题
问题描述
给定一个 m x n 的网格,其中每个单元格包含一个非负整数,表示到达该单元格的费用。同时,网格中可能存在若干不可通行的障碍物,障碍物用 -1 表示。你的任务是找到从左上角 (0, 0) 到右下角 (m-1, n-1) 的路径,使得路径上的数字总和最小。如果不存在路径,请返回 -1。
输入
- 一个二维数组
grid,grid[i][j]为网格中的数值,其中grid[i][j] >= 0表示可通行,grid[i][j] == -1表示不可通行的障碍物。
输出
- 返回从左上角到右下角的路径上的数字总和的最小值。如果不存在这样的路径,返回
-1。
示例 1
输入
grid = [[1, 3, 1],[1, -1, 1],[4, 2, 1]
]
输出
7
解释
最优路径为 (0,0) -> (1,0) -> (2,0) -> (2,1) -> (2,2),路径费用为 1 + 1 + 4 + 1 + 1 = 7。
当然可以,这里是一个包含不可通行案例的示例:
示例 2
输入
grid = [[1, 3, -1],[2, -1, 3],[-1, 2, 1]
]
输出
-1
解释
在这个网格中,位置 (2, 0), (1, 1), (0,2) 是一个障碍物,导致从左上角 (0, 0) 到右下角 (2, 2) 的路径不可达,因此返回 -1。
这样是否满足你的要求?
提示
m和n的范围是[1, 100]。- 网格中的数值在
[0, 100]范围内。
2.2 拓展解题代码
#include <vector>
#include <algorithm>
#include <iostream>
using namespace std;/*** 基于力扣64题的变形题,详情请参考:https://smileyan.blog.csdn.net/article/details/142346755*/class Solution {
public:int minPathSum(vector<vector<int>>& grid) {int row = grid.size();int column = grid[0].size();vector<vector<int>> dp(row, vector<int>(column));dp[0][0] = grid[0][0];// 第一行每个点的最小路径int barricade = -1;for (int i = 1; i < column; i++) {if (dp[0][i - 1] == barricade || grid[0][i] == barricade) {dp[0][i] = barricade;} else {dp[0][i] = grid[0][i] + dp[0][i - 1];}}// 第一列每个点的最小路径for (int i = 1; i < row; i++) {if (dp[i - 1][0] == barricade || grid[i][0] == barricade) {dp[i][0] = barricade;} else {dp[i][0] = grid[i][0] + dp[i - 1][0];}}/** 对于 dp[i][k] 的计算规则为* dp[i][k] = min(dp[i - 1][k], dp[i][k - 1]) + grid[i][k]*/for (int i = 1; i < row; i++) {for (int k = 1; k < column; k++) {if (grid[i][k] == barricade || (dp[i - 1][k] == barricade && dp[i][k - 1] == barricade)) {dp[i][k] = barricade;} else if (dp[i - 1][k] == barricade) {dp[i][k] = dp[i][k - 1] + grid[i][k];} else if (dp[i][k - 1] == barricade) {dp[i][k] = dp[i - 1][k] + grid[i][k];} else {dp[i][k] = min(dp[i - 1][k], dp[i][k - 1]) + grid[i][k];}}}return dp[row - 1][column - 1];}
};int main() {Solution solution;vector<vector<int>> grid1 = {{1, 3, 1},{1, 5, 1},{4, 2, 1}};int result1 = solution.minPathSum(grid1);cout<<result1<<" -> 7"<<endl;vector<vector<int>> grid2 = {{1, 2, 3},{4, 5, 6}};int result2 = solution.minPathSum(grid2);cout<<result2<<" -> 12"<<endl;vector<vector<int>> grid3 = {{1, -1, 3},{4, -1, 6}};int result3 = solution.minPathSum(grid3);cout<<result3<<" -> -1"<<endl;vector<vector<int>> grid4 = {{1, -1, 3},{4, 1, 6}};int result4 = solution.minPathSum(grid4);cout<<result4<<" -> 12"<<endl;vector<vector<int>> grid5 = {{1, 3, 1},{1, 5, 2},{-1, 2, 1}};int result5 = solution.minPathSum(grid5);cout<<result5<<" -> 8"<<endl;vector<vector<int>> grid6 = {{1, 3, -1},{1, -1, 2},{-1, 2, 1}};int result6 = solution.minPathSum(grid6);cout<<result6<<" -> -1"<<endl;vector<vector<int>> grid7 = {{-1, 3, 1},{1, 1, 2},{1, 2, 1}};int result7 = solution.minPathSum(grid7);cout<<result7<<" -> -1"<<endl;vector<vector<int>> grid8 = {{1, 3, 1},{1, 1, 2},{1, 2, -1}};int result8 = solution.minPathSum(grid8);cout<<result8<<" -> -1"<<endl;return 0;
}
3. 总结
这道题应当与力扣第70题(爬楼梯)一样,作为动态规划的典型问题(热题100中多维动态规划类)。基于这道题面试官现场做了一个简单的调整,并不要求应聘者直接写代码求解出来,而是希望应聘者给出解决方案,并解释方案的可行性。
接下来的时间,还将围绕着这道题进行更多的摸索,动态规划是一个非常有意思的题:常常会因为阅读了 “参考答案” 而感到震惊。“怎么会这么简单”、“原来如此”。
感谢您的阅读、评论与点赞支持 ~ 感谢 ~
Smileyan
2024.09.21 23:48
相关文章:

【多维动态规划】64. 最小路径和(面试真题+面试官调整后的题目)
64. 最小路径和 难度:中等 力扣地址:https://leetcode.cn/problems/minimum-path-sum/description/ 1. 原题以及解法 1.1 题目 给定一个包含非负整数的 m x n 网格 grid ,请找出一条从左上角到右下角的路径,使得路径上的数字总和…...

Web后端开发技术:RESTful 架构详解
RESTful 是一种基于 REST(表述性状态转移,Representational State Transfer)架构风格的 API 设计方式,通常用于构建分布式系统,特别是在 Web 应用开发中广泛应用。REST 是一种轻量级的架构模式,利用标准的 …...

【Fastapi】参数获取,json和query
【Fastapi】参数获取,json和query 前言giteegithub query形式json传递同步方法使用json 前言 花了半个月的时间看了一本小说,懈怠了…今天更新下fastapi框架的参数获取 gitee https://gitee.com/zz1521145346/fastapi_frame.git github https://git…...

【Node.js】初识微服务
概述 Node.js 的微服务架构是一种通过将应用程序分解为独立的、松耦合的小服务的方式进行系统设计。 每个微服务负责处理一个特定的业务功能,并且这些服务可以独立开发、部署、扩展和管理,并且可以通讯。 它的核心思想就是解耦。 微服务和微前端是类…...
)
React项目实战(React后台管理系统、TypeScript+React18)
### 项目地址:(线上发布) (1)别人的项目地址 gitgitee.com:zqingle/lege-react-management.git (2)我自己的项目地址 gitgitee.com:huihui-999/lege-react-management.git ### B站讲解视频地址 https://www.bilibili.com/video/BV1FV4y157Zx?p37&spm_id_frompageDrive…...

【专题】2024中国生物医药出海现状与趋势蓝皮书报告合集PDF分享(附原数据表)
原文链接:https://tecdat.cn/?p37719 出海已成为中国医药产业实现提速扩容的重要途径。目前,中国医药产业发展态势良好,创新能力不断增强,然而也面临着医保政策改革和带量集采带来的压力。政府积极出台多项政策支持医药企业出海…...

【iOS】KVC
文章目录 KVC的定义 容器类中KVC的实现 KVC设值 KVC取值 KVC使用KeyPath KVC处理异常 KVC处理设值nil异常 KVC处理UndefinedKey异常 KVC处理数值和结构体类型属性 KVC键值验证 KVC处理集合 简单集合运算符 对象运算符 KVC处理字典 KVC应用 动态地取值和设值 用…...

【2024年华为杯研究生数学建模竞赛C题】完整论文与代码
这里写目录标题 基于数据驱动下磁性元件的磁芯损耗建模一、问题重述1.1问题背景1.2问题回顾 问题分析与模型假设模型建立与求解 基于数据驱动下磁性元件的磁芯损耗建模 一、问题重述 1.1问题背景 在现代电力电子和变压器设计中,磁性元件是确保能量高效传递和系统稳…...

svn回退到以前历史版本修改并上传
svn回退到以前版本,并在以前版本上修改代码后,上传到svn库当中,如下步骤: 3、 以回退到版本号4为例:选中版本号4,右键->Revert to this version,在出现的对话框中 点击yes! 4、 5、...
fiddler抓包07_抓IOS手机请求
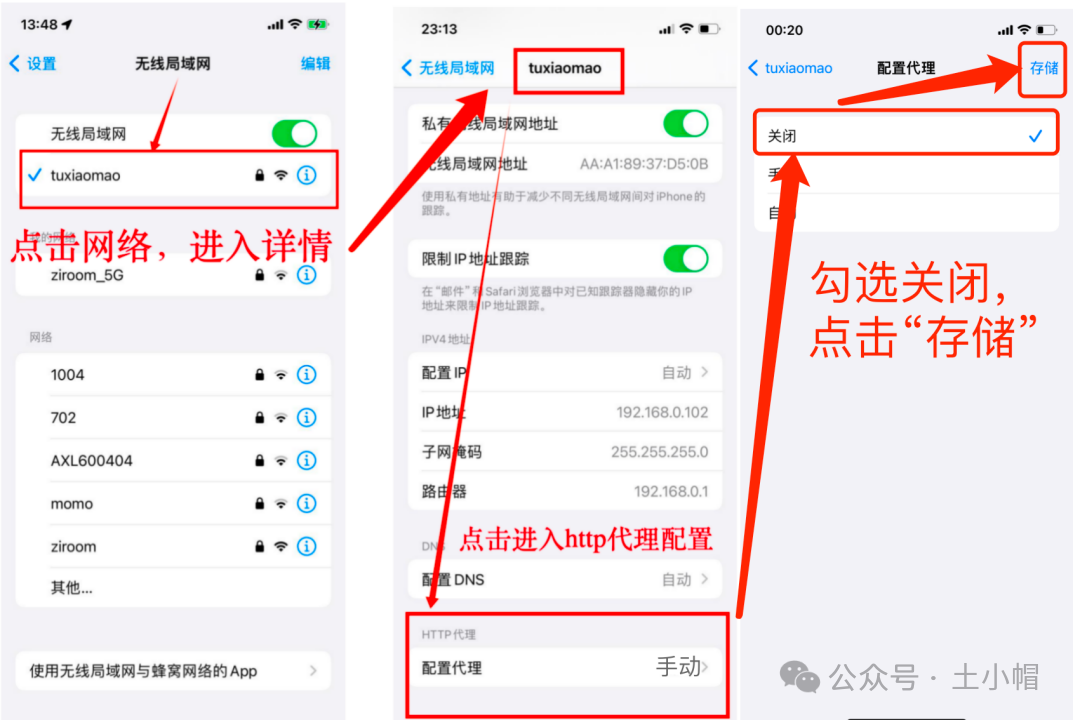
课程大纲 前提:电脑和手机连接同一个局域网 (土小帽电脑和手机都连了自己的无线网“tuxiaomao”。) 原理如下: 电脑浏览器抓包时,直接就是本机网络。手机想被电脑Fiddler抓包,就要把Fiddler变成手机和网络…...

Windows系统及Ubuntu系统安装Java
Java语言简介 Java是一种高级编程语言,Java语言的创始可以追溯到1990年代初,当时任职于Sun Microsystems(后来被甲骨文公司收购)的詹姆斯高斯林(James Gosling)等人开始开发一种名为“Oak”(名字来源于詹姆…...

uni-data-select 使用 localdata 传入数据出现 不回显 | 下拉显示错误的 解决方法
目录 1. 问题所示2. 正确Demo3. 下拉显示错误(Bug复现)4. 下拉不回显(Bug复现)1. 问题所示 uni-app的下拉框uni-data-select 使用 localdata 传入数据 主要总结正确的Demo以及复现一些Bug 数据不回显数据不显示下拉选项2. 正确Demo 详细的基本知识推荐阅读:uni-app中的…...

图解 TCP 四次挥手|深度解析|为什么是四次|为什么要等2MSL
写在前面 今天我们来图解一下TCP的四次挥手、深度解析为什么是四次? 上一片文章我们已经介绍了TCP的三次握手 解析四次挥手 数据传输完毕之后,通信的双方都可释放连接。现在客户端A和服务端B都处于ESTABLISHED状态。 第一次挥手 客户端A的应用进…...
DevExpress中文教程:如何将WinForms数据网格连接到ASP. NET Core WebAPI服务?
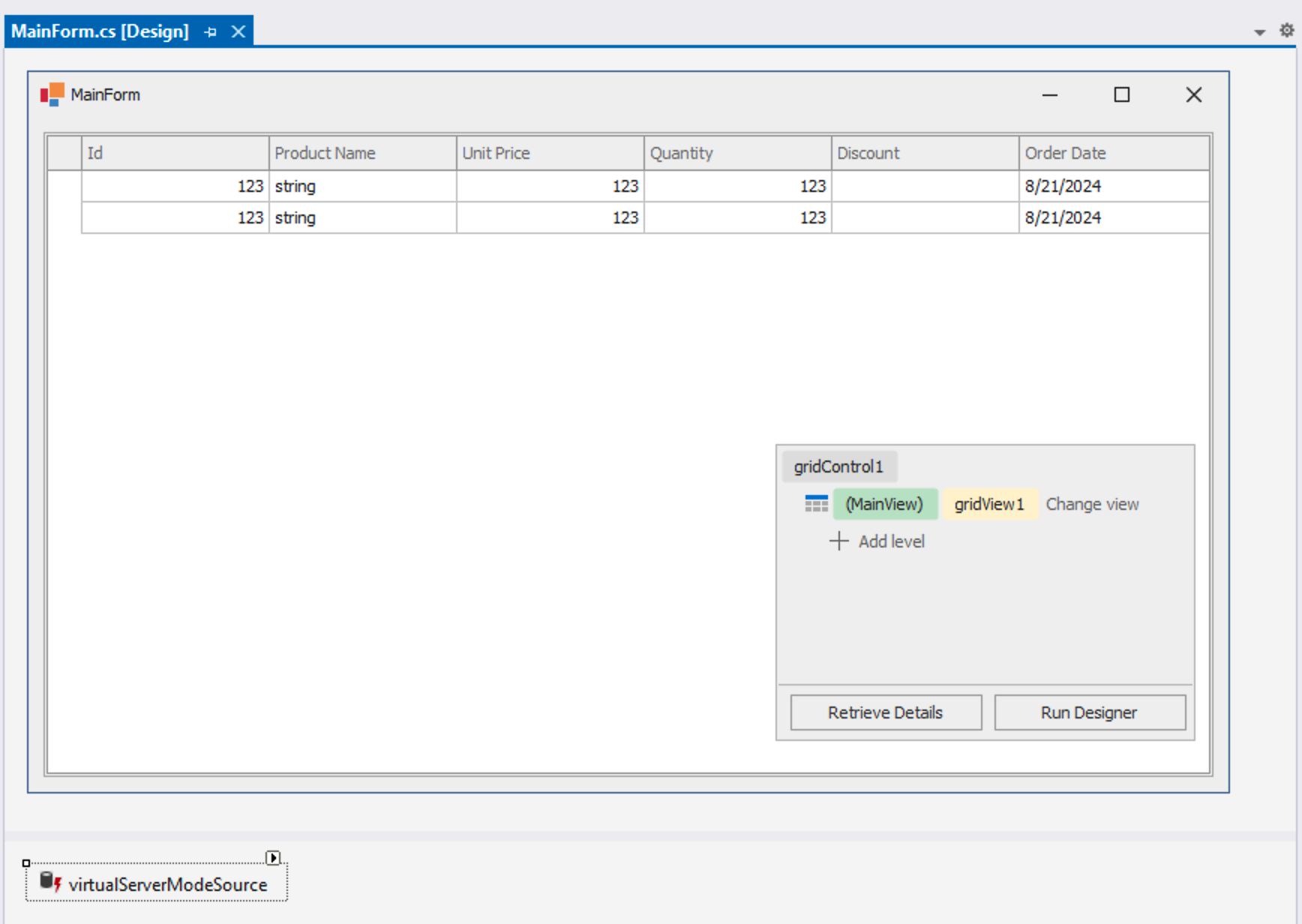
日前DevExpress官方发布了DevExpress WinForms的后续版本——将.NET桌面客户端连接到安全后端Web API服务(EF Core with OData),在本文中我们将进一步演示如何使用一个更简单的服务来设置DevExpress WinForms数据网格。 P.S:DevExpress WinForms拥有180…...

SpringBoot3核心特性-核心原理
目录 传送门前言一、事件和监听器1、生命周期监听2、事件触发时机 二、自动配置原理1、入门理解1.1、自动配置流程1.2、SPI机制1.3、功能开关 2、进阶理解2.1、 SpringBootApplication2.2、 完整启动加载流程 三、自定义starter1、业务代码2、基本抽取3、使用EnableXxx机制4、完…...

Linux:RPM软件包管理以及yum软件包仓库
挂载光驱设备 RPM软件包管理 RPM软件包简介 区分软件名和软件包名 软件名:firefox 软件包名:firefox-52.7.0-1.el7.centos.x86_64.rpm 查询软件信息 查询软件(参数为软件名) ]# rpm -qa #当前系统中所有已安装的软件包 ]# r…...

pod介绍与配置
1、pod概念介绍 Pod 是 kubernetes 基本调度单位。每个 Pod 中可以运 行一个或多个容器,共享 Pod 的文件系统、IP 和网络等资源,每个 Pod 只有一个 IP。 2、使用 yaml或json 文件创建 Pod 声明式文件方式创建 Pod,支持 yaml 和 json 1&…...

【Taro】初识 Taro
笔记来源:编程导航。 概述 Taro 官方文档:https://taro-docs.jd.com/docs/ (跨端开发框架) Taro 官方框架兼容的组件库: taro-ui:https://taro-ui.jd.com/#/ (最推荐,兼容性最好&…...

【设计模式-备忘录】
备忘录模式(Memento Pattern)是一种行为型设计模式,用于保存对象的内部状态,以便在将来某个时间可以恢复到该状态,而不暴露对象的内部实现细节。备忘录模式特别适合在需要支持撤销(Undo)操作的应…...

【数据结构】排序算法系列——快速排序(附源码+图解)
快速排序 接下来我们将要介绍的是排序中最为重要的算法之一——快速排序。 快速排序(英语:Quicksort),又称分区交换排序(partition-exchange sort),最早由东尼霍尔提出。快速排序通常明显比其…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

在WSL2的Ubuntu镜像中安装Docker
Docker官网链接: https://docs.docker.com/engine/install/ubuntu/ 1、运行以下命令卸载所有冲突的软件包: for pkg in docker.io docker-doc docker-compose docker-compose-v2 podman-docker containerd runc; do sudo apt-get remove $pkg; done2、设置Docker…...
