整数二分算法和浮点数二分算法
整数二分算法和浮点数二分算法
二分
现实中运用到二分的就是猜数字的游戏 假如有A同学说B同学所说数的大小,B同学要在1~100中间猜中数字65,当B同学每次说的数都是范围的一半时这就算是一个二分查找的过程

二分查找的前提是这个数字序列要有单调性
基本步骤
初始化:
设定两个指针,left 和 right,分别指向数组的起始和末尾。
计算中间位置:
使用公式 mid = left + (right - left) / 2 或者left+right>>1计算中间位置。
比较:
如果中间位置的元素等于目标值,返回中间位置。
如果目标值小于中间位置的元素,则将 right 更新为 mid - 1,继续在左半部分查找。
如果目标值大于中间位置的元素,则将 left 更新为 mid + 1,继续在右半部分查找。
重复:
重复步骤 2 和 3,直到 left 超过 right。
结束:
如果在查找过程中未找到目标值,返回一个表示未找到的结果(如 -1 或 None)。
二分查找算法的时间复杂度是 O(log n),非常高效。
整数二分
二分的本质并不是一定要单调,而是对一个区间可以化分成两个部分,一部分一定满足条件,另一部分一定不满足,对于满足这种条件的我们可以找出两个边界点,这样的话二分算法可以寻找这个性质的边界(红色和黑色的边界都行,因为是整数二分所以两边界不重合)。

第一种情况(二分左半部分)
假如说有一串数字1,2,3,3,4,4,5,6,8,8我们需要找到满足小于等于3的最大情况的子序列,也就是我们需要找到最后一次出现的3,我们可以如何做呢?
我们让一个mid=(l+r+1)/2 假如说a[mid]<=3,此时if(check(mid))==true说明此时mid指向的值可能是答案,但是我们无法保证其后面还有没有答案是<=3的,所以此时应该是l=mid,假如说此时a[mid]>=3,if(check(mid))==false说明此时mid指向的是一定不满足条件的的那么此时应该是r=mid-1。

我们继续不段重复以上操作直到l>=r时退出循环。
第二种情况(二分右半部分)
还是这个数字序列这次我们要找1,2,3,3,4,4,5,6,8,8中第一次出现3的位置,我们应该怎么做呢?
我们还是让一个mid=(l+r)/2 假如说a[mid]>=3,此时if(check(mid))==true说明此时mid指向的值可能是答案,但是我们无法保证其前面还有没有答案是>=3的,所以此时应该是r=mid,假如说此时a[mid]<=3,if(check(mid))==false说明此时mid指向的是一定不满足条件的的那么此时应该是l=mid+1。
注意:第一种情况是(l+r+1)而不是(l+r)为为什么呢?
因为计算机的除法都是向下取整的所以就会出现问题,假如说此时l=r-1那么mid=(l+r)/2=(l+l+1)/2=l然后我们假如发现l还是满足条件的,那么此时就会陷入l=mid,mid=l的死循环
我们来写一道题
洛谷P2249
下面的代码是既有第一次出现,也有最后一次出现的,两种情况都写了。
代码如下:
#include <iostream>
using namespace std;const int N = 1e5 + 10; // 定义数组的最大容量,数组a最多可以存放1e5个元素
int a[N], n, m; // 定义全局变量数组a,n为数组长度,m为查询次数// check1函数用于检查a[mid]是否大于等于目标值x
bool check1(int mid, int x) {if (a[mid] >= x) {return true; // 如果a[mid]大于等于x,返回true,表示满足条件} else {return false; // 否则返回false,表示不满足条件}
}// check2函数用于检查a[mid]是否小于等于目标值x
bool check2(int mid, int x) {if (a[mid] <= x) {return true; // 如果a[mid]小于等于x,返回true,表示满足条件} else {return false; // 否则返回false,表示不满足条件}
}int main() {cin >> n >> m; // 输入数组的长度n和查询的次数mfor (int i = 1; i <= n; i++) {cin >> a[i]; // 依次输入数组a的元素}while (m--) { // 对每一次查询进行处理,m次查询int x; // 定义要查询的目标值xcin >> x; // 输入目标值x// 首先进行二分查找,寻找第一个大于等于x的位置int l = 1, r = n; // 初始化左右边界,l是左边界,r是右边界while (l < r) { // 当左边界小于右边界时,继续二分查找int mid = (l + r) >> 1; // 计算中间位置midif (check1(mid, x)) { // 如果a[mid]大于等于xr = mid; // 缩小右边界至mid} else {l = mid + 1; // 否则缩小左边界至mid+1}}// 查找完成后,检查a[l]是否等于目标值xif (a[l] == x) {cout << l << " "; // 如果a[l]等于x,输出位置l} else {cout << -1 << " "; // 如果a[l]不等于x,输出-1表示未找到}// 再进行一次二分查找,寻找最后一个小于等于x的位置l = 1, r = n; // 重新初始化左右边界while (l < r) {int mid = (l + r + 1) >> 1; // 计算中间位置mid,向上取整if (check2(mid, x)) { // 如果a[mid]小于等于xl = mid; // 缩小左边界至mid} else {r = mid - 1; // 否则缩小右边界至mid-1}}// 查找完成后,再次检查a[l]是否等于目标值xif (a[l] == x) {cout << l << " "; // 如果a[l]等于x,输出找到的最后位置l} else {cout << -1 << " "; // 如果没找到,输出-1}cout<<endl;}
}
整数二分模板
bool check(int x) {// 这里是判断x是否满足某种性质的函数,具体实现取决于实际问题// 可以根据x的值来返回true或false,用于二分查找中的判断/* ... */
}// 区间[l, r]被划分为[l, mid]和[mid + 1, r]时使用的二分查找
int bsearch_1(int l, int r) {// 二分查找的目的是在区间[l, r]中寻找满足某种性质的最小位置// l 是左边界,r 是右边界,最终返回满足性质的最小下标while (l < r) { // 当左边界小于右边界时,继续进行二分查找int mid = (l + r) >> 1; // 计算中间位置mid,使用右移操作进行快速计算,相当于 (l + r) / 2if (check(mid)) { // 如果check(mid)为true,表示mid满足性质r = mid; // 将右边界缩小到mid,因为我们要找满足性质的最小位置} else { // 否则,mid不满足性质l = mid + 1; // 将左边界缩小到mid + 1,因为mid以及它左边的值都不满足条件}}return l; // 返回最终的左边界,此时l == r,且为满足性质的最小位置
}// 区间[l, r]被划分为[l, mid - 1]和[mid, r]时使用的二分查找
int bsearch_2(int l, int r) {// 二分查找的目的是在区间[l, r]中寻找满足某种性质的最大位置// l 是左边界,r 是右边界,最终返回满足性质的最大下标while (l < r) { // 当左边界小于右边界时,继续进行二分查找int mid = (l + r + 1) >> 1; // 计算中间位置mid,并向上取整,确保mid偏向右侧if (check(mid)) { // 如果check(mid)为true,表示mid满足性质l = mid; // 将左边界缩小到mid,因为我们要找满足性质的最大位置} else { // 否则,mid不满足性质r = mid - 1; // 将右边界缩小到mid - 1,因为mid以及它右边的值都不满足条件}}return l; // 返回最终的左边界,此时l == r,且为满足性质的最大位置
}
浮点数二分算法
浮点数二分相较于整数二分更加简单因为只有一个模板,并且没有边界问题,浮点数的二分查找可以用于求解需要精确值的问题,例如求方程的解或几何问题中涉及浮点精度的求解。与整数二分查找不同,浮点数二分查找必须考虑精度问题,因为浮点数无法精确到某个具体值,所以我们需要一个精度(如 epsilon),用于判断二分查找的终止条件。
假如说我们需要找一个数x的平方等于目标值2
代码如下:
#include <iostream>
#include <cmath> // 包含abs函数,用于计算绝对值
using namespace std;// 定义一个需要使用二分法求解的函数,返回值为目标函数值
double f(double x) {// 举例:寻找函数 f(x) = x^2 - 2 的根return x * x - 2;
}int main() {double l = 0, r = 2; // 初始区间[l, r],假设根位于[0, 2]之间double eps = 1e-7; // 定义精度eps,即当结果误差小于1e-7时停止迭代// 当区间宽度大于精度要求时,继续二分while (r - l > eps) {double mid = (l + r) / 2; // 计算中间值if (f(mid) > 0) { // 如果 f(mid) > 0,表示 mid 处的值在根的右侧r = mid; // 缩小右边界至mid} else { // 否则 f(mid) <= 0,表示 mid 处的值在根的左侧或是根l = mid; // 缩小左边界至mid}}// 输出结果,l 和 r 最终都会逼近根cout << "x ≈ " << l << endl;cout << "验证结果: f(x) = " << f(l) << endl; // 输出验证f(l)接近0
}
浮点数二分模板
// 函数原型:在浮点数区间 [l, r] 上使用二分查找,找到满足某种性质的浮点数
double bsearch_3(double l, double r)
{const double eps = 1e-6; // eps 是精度控制的参数,当区间长度小于 eps 时停止二分查找// 1e-6 表示小数点后 6 位精度,可根据题目要求调整精度// 当区间长度大于 eps 时,继续进行二分查找while (r - l > eps){// 计算区间的中点 middouble mid = (l + r) / 2;// 调用 check 函数判断 mid 是否满足给定的性质// 假设 check(mid) 返回 true,则意味着 mid 及其右侧可能满足性质,// 因此将右区间收缩到 mid,继续在左侧区间 [l, mid] 上搜索if (check(mid)) r = mid;// 否则,mid 及其左侧不满足性质,因此我们将左区间收缩到 mid,继续在右侧区间 [mid, r] 上搜索else l = mid;}// 最后返回左边界 l(或右边界 r),此时区间已经很小,接近于精度要求的结果// 因为 l 和 r 的距离非常小,最终答案应为 l 或 r 的近似值return l;
}
整数二分算法和浮点数二分算法源代码
相关文章:

整数二分算法和浮点数二分算法
整数二分算法和浮点数二分算法 二分 现实中运用到二分的就是猜数字的游戏 假如有A同学说B同学所说数的大小,B同学要在1~100中间猜中数字65,当B同学每次说的数都是范围的一半时这就算是一个二分查找的过程 二分查找的前提是这个数字序列要有单调性 基…...

智能回收箱的功能和使用步骤介绍
智能回收箱是现代城市环保与资源循环利用领域的一项创新技术,它通过集成各种智能化功能,提高了垃圾回收的效率和准确性,促进了垃圾分类与减量。随着全球对环境保护意识的增强和智慧城市概念的推广,智能回收箱的发展前景非常广阔&a…...

Remix在SPA模式下,出现ErrorBoundary错误页加载Ant Design组件报错,不能加载样式的问题
Remix是一个既能做服务端渲染,又能做单页应用的框架,如果想做单页应用,又想学服务端渲染,使用Remix可以降低学习成本。最近,在学习Remix的过程中,遇到了在SPA模式下与Ant Design整合的问题。 我用Remix官网…...

ADB ROOT开启流程
开启adb root 选项后,执行如下代码: packages/apps/Settings/src/com/android/settings/development/AdbRootPreferenceController.java mADBRootService new ADBRootService(); Override public boolean onPreferenceChange(Preference preference…...

传输层协议 —— TCP协议(上篇)
目录 1.认识TCP 2.TCP协议段格式 3.可靠性保证的机制 确认应答机制 超时重传机制 连接管理机制 三次握手 四次挥手 1.认识TCP 在网络通信模型中,传输层有两个经典的协议,分别是UDP协议和TCP协议。其中TCP协议全称为传输控制协议(Tra…...

YOLOv8改进,YOLOv8的Neck替换成AFPN(CVPR 2023)
摘要 多尺度特征在物体检测任务中对编码具有尺度变化的物体非常重要。多尺度特征提取的常见策略是采用经典的自上而下和自下而上的特征金字塔网络。然而,这些方法存在特征信息丢失或退化的问题,影响了非相邻层次的融合效果。一种渐进式特征金字塔网络(AFPN),以支持非相邻…...

学习大数据DAY59 全量抽取和增量抽取实战
目录 需求流程: 需求分析与规范 作业 作业2 需求流程: 全量抽取 增量抽取 - DataX Kettle Sqoop ... 场景: 业务部门同事或者甲方的工作人员给我们的部门经理和你提出了新的需 求 流程: 联系 > 开会讨论 > 确认需求 > 落地 需求文档( 具体…...

YOLOv8——测量高速公路上汽车的速度
引言 在人工神经网络和计算机视觉领域,目标识别和跟踪是非常重要的技术,它们可以应用于无数的项目中,其中许多可能不是很明显,比如使用这些算法来测量距离或对象的速度。 测量汽车速度基本步骤如下: 视频采集&#x…...

在线相亲交友系统:寻找另一半的新方式
在这个快节奏的时代里,越来越多的单身男女发现,传统意义上的相亲方式已经难以满足他们的需求。与此同时,互联网技术的迅猛发展为人们提供了新的社交渠道——在线相亲交友系统作者h17711347205。本文将探讨在线相亲交友系统如何成为一种寻找另…...

MySQL 中存储过程参数的设置与使用
《MySQL 中存储过程参数的设置与使用》 在 MySQL 数据库中,存储过程是一组预先编译好的 SQL 语句集合,可以接受参数并返回结果。使用存储过程可以提高数据库的性能和可维护性,同时也可以减少网络流量和代码重复。那么,如何在 MyS…...

2k1000LA 调试HDMI
问题: 客户需要使用HDMI 接口,1080p 的分辨率。 ---------------------------------------------------------------------------------------------------------------- 这里需要看看 龙芯派的 demo 版 的 硬件上的连接。 硬件上: 官方的demo 板 , dvo1 应该是 HDMI的…...

24年蓝桥杯及攻防世界赛题-MISC-1
2 What-is-this AZADI TOWER 3 Avatar 题目 一个恐怖份子上传了这张照片到社交网络。里面藏了什么信息?隐藏内容即flag 解题 ┌──(holyeyes㉿kali2023)-[~/Misc/tool-misc/outguess] └─$ outguess -r 035bfaa85410429495786d8ea6ecd296.jpg flag1.txt Reading 035bf…...

前端项目代码开发规范及工具配置
在项目开发中,良好的代码编写规范是项目组成的重要元素。本文将详细介绍在项目开发中如何集成相应的代码规范插件及使用方法。 项目规范及工具 集成 EditorConfig集成 Prettier1. 安装 Prettier2. 创建 Prettier 配置文件3. 配置 .prettierrc4. 使用 Prettier 集成 …...
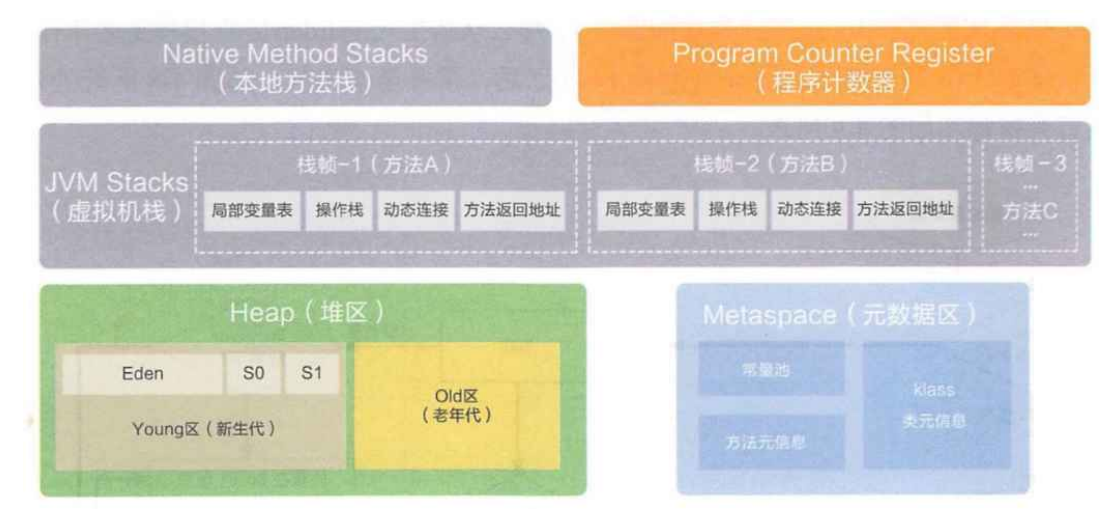
【JVM】JVM执行流程和内存区域划分
文章目录 是什么JVM 执行流程内存区域划分堆栈程序计数器元数据区经典笔试题 是什么 Java 虚拟机 JDK,Java 开发工具包JRE,Java 运行时环境JVM,Java 虚拟机 JVM 就是 Java 虚拟机,解释执行 Java 字节码 JVM 执行流程 编程语言…...
Python | 读取.dat 文件
写在前面 使用matlab可以输出为 .dat 或者 .mat 形式的文件,之前介绍过读取 .mat 后缀文件,今天正好把 .dat 的读取也记录一下。 读取方法 这里可以使用pandas库将其作为一个dataframe的形式读取进python,数据内容格式如下,根据…...

信息技术的变革与未来发展的思考
信息技术的变革与未来发展的思考 在21世纪,信息技术(IT)正在以前所未有的速度推动社会、经济、文化的深刻变革。无论是人工智能、大数据,还是云计算、物联网,信息技术的发展已经渗透到了各个行业,彻底改变…...

融会贯通记单词,绝对丝滑,一天轻松记几百
如果我将flower(花)、flat(公寓)、floor(地板)、plane(飞机)几个单词放在一起,你会怎么来记忆这样的一些单词呢? 我们会发现,我们首先可以将plane去掉,因为它看上去几乎就是一个异类。这样,我们首先就可以将…...

【计算机视觉】YoloV8-训练与测试教程
✨ Blog’s 主页: 白乐天_ξ( ✿>◡❛) 🌈 个人Motto:他强任他强,清风拂山冈! 💫 欢迎来到我的学习笔记! 制作数据集 Labelme 数据集 数据集选用自己标注的,可参考以下:…...

响应式布局-媒体查询父级布局容器
1.响应式布局容器 父局作为布局容器,配合自己元素实现变化效果,原理:在不通过屏幕下面吗,通过媒体查询来改变子元素的排列方式和大小,从而实现不同尺寸屏幕下看到不同的效果。 2.响应尺寸布局容器常见宽度划分 手机-…...

Android APN type 配置和问题
问题/疑问 如果APN配置了非法类型(代码没有定义的),则APN匹配加载的时候最终结果会是空类型。 那么到底是xml解析到数据库就是空type呢?还是Java代码匹配的时候映射是空的呢? Debug Log 尝试将原本的APN type加入ota或者新建一条ota type APN,检查log情况。 //Type有…...

挑战杯推荐项目
“人工智能”创意赛 - 智能艺术创作助手:借助大模型技术,开发能根据用户输入的主题、风格等要求,生成绘画、音乐、文学作品等多种形式艺术创作灵感或初稿的应用,帮助艺术家和创意爱好者激发创意、提高创作效率。 - 个性化梦境…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...
