代码随想录算法训练营第五十六天|583. 两个字符串的删除操作、72. 编辑距离
LeetCode 583 两个字符串的删除操作
题目链接:https://leetcode.cn/problems/delete-operation-for-two-strings/
思路:
方法一:两个子串同时删除元素
-
dp数组的含义
dp[i][j]dp[i][j]dp[i][j]代表以i-1为结尾的字符串word1,和以j-1位结尾的字符串word2,想要达到相等,所需要删除元素的最少次数 -
递推公式
本题有两种情况:
word1[i - 1] == word2[j - 1]
显然此时递推公式为:
dp[i][j]=dp[i−1][j−1]+1dp[i][j] = dp[i-1][j-1]+1dp[i][j]=dp[i−1][j−1]+1
word1[i - 1] != word2[j - 1]
此时有三种情况:
1. 删除word1里的第i-1个元素
dp[i][j]=dp[i−1][j]+1dp[i][j] = dp[i-1][j]+1dp[i][j]=dp[i−1][j]+1
2. 删除word2里的第i-1个元素
dp[i][j]=dp[i][j−1]+1dp[i][j] = dp[i][j-1]+1dp[i][j]=dp[i][j−1]+1
3. 同时删除word1和word2里的第i-1个元素
dp[i][j]=dp[i−1][j−1]+1dp[i][j] = dp[i-1][j-1]+1dp[i][j]=dp[i−1][j−1]+1
因为要求的是最小值,所以总的递推公式为:
dp[i][j]=min(dp[i−1][j]+1,dp[i][j−1]+1,dp[i−1][j−1]+1)dp[i][j] = min({dp[i-1][j]+1, dp[i][j-1]+1, dp[i-1][j-1]+1})dp[i][j]=min(dp[i−1][j]+1,dp[i][j−1]+1,dp[i−1][j−1]+1) -
初始化
dp[i][0]dp[i][0]dp[i][0]代表word1要和空字符相等需要多少次删除操作,显然为i;同理,dp[0][j]dp[0][j]dp[0][j]代表word2要和空字符 相等需要多少次删除操作,显然为j,所以初始化操作如下:for(int i = 0; i <= word1.size(); i++) dp[i][0] = i; for(int j = 0; j <= word2.size(); j++) dp[0][j] = j; -
遍历顺序
显然遍历是从上到下,从左到右
代码:
class Solution {
public:int minDistance(string word1, string word2) {vector<vector<int>>dp(word1.size() + 1, vector<int>(word2.size() + 1, 0));for(int i = 0; i <= word1.size(); i++) dp[i][0] = i;for(int j = 0; j <= word2.size(); j++) dp[0][j] = j;for(int i = 1; i <= word1.size(); i++){for(int j = 1; j <= word2.size(); j++){if(word1[i - 1] == word2[j - 1])dp[i][j] = dp[i - 1][j - 1];elsedp[i][j] = min({dp[i][j - 1] + 1, dp[i - 1][j] + 1, dp[i - 1][j - 1] + 2});}}return dp[word1.size()][word2.size()];}
};
方法二:求出最长公共子序后,两个字符串分别减去最长公共子序的长度
- dp数组的含义
dp[i][j]dp[i][j]dp[i][j]代表以i-1为结尾的字符串word1,和以j-1位结尾的字符串word2的最长公共子序的长度 - 递推公式
本题有两种情况:
word1[i - 1] == word2[j - 1]
显然此时递推公式为:
dp[i][j]=dp[i−1][j−1]+1dp[i][j] = dp[i-1][j-1]+1dp[i][j]=dp[i−1][j−1]+1
word[i - 1] != word[j - 1]
例子:text1:abc text2:ace
有两种情况:
因为最后c和e不相同,所以可以是abc和ac相比,得出公共子序列的长度,也可以是ab和ace相比
所以此时递推公式是:
dp[i][j]=max(dp[i][j−1],dp[i−1][j])dp[i][j] = max(dp[i][j-1],dp[i-1][j])dp[i][j]=max(dp[i][j−1],dp[i−1][j]) - 初始化
dp[i][0]和dp[0][j]显然都是没有意义的,即二维数组的第一行和第一列,将其全部初始化为0即可。其余数值因为会在递推公式中被覆盖,所以也都初始化为0,这样可以使得代码相对简洁。 - 遍历顺序
显然遍历是从上到下,从左到右
代码
class Solution {
public:int minDistance(string word1, string word2) {vector<vector<int>>dp(word1.size() + 1, vector<int>(word2.size() + 1, 0));for(int i = 1; i <= word1.size(); i++){for(int j = 1; j <= word2.size(); j++){if(word1[i - 1] == word2[j - 1])dp[i][j] = dp[i - 1][j - 1] + 1;elsedp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);}}int result = word1.size() + word2.size() - 2 * dp[word1.size()][word2.size()];return result;}
};
总结
想到了第二种方法,第一种方法不相等时候的情况没有考虑清楚。
LeetCode 72 编辑距离
题目链接:https://leetcode.cn/problems/edit-distance/
思路:
-
dp数组的含义
dp[i][j]dp[i][j] 表示以下标i-1为结尾的字符串word1变为以下标j-1为结尾的字符串word2的最小的操作数为。 -
递推公式
本题有两种情况:
word1[i - 1] == word2[j - 1]
此时说明需要继续向后修改即可。
所以此时递推公式为:
dp[i][j]=dp[i−1][j−1]dp[i][j] = dp[i-1][j-1]dp[i][j]=dp[i−1][j−1]word1[i - 1] != word2[j - 1]
有三种操作方法:
1. 删除word1的第i-1个元素
此时递推公式为:
dp[i][j]=dp[i−1][j]+1dp[i][j] = dp[i-1][j]+1dp[i][j]=dp[i−1][j]+1
2. 替换word1的第i-1个元素
那么就要在dp[i−1][j−1]dp[i-1][j-1]dp[i−1][j−1](以i-2为结尾的word1子串和以j-2结尾的word2子串)的基础上对word1的第i-1个元素进行操作,所以此时递推公式为:
dp[i][j]=dp[i−1][j−1]+1dp[i][j] = dp[i-1][j-1]+1dp[i][j]=dp[i−1][j−1]+1
3. 在word1的第i-2个元素后添加一个元素
在word1添加一个元素,相当于word2删除一个元素,例如 word1 = “a” ,word2 = “ad”,word2删除元素’d’ 和 word1添加一个元素’d’,变成word1=“ad”, word2=“a”, 最终的操作数是一样!
所以此时递推公式为:
dp[i][j]=dp[i][j−1]+1dp[i][j] = dp[i][j-1]+1dp[i][j]=dp[i][j−1]+1
dp数组如下图所示意a a d+-----+-----+ +-----+-----+-----+| 0 | 1 | | 0 | 1 | 2 |+-----+-----+ ===> +-----+-----+-----+a | 1 | 0 | a | 1 | 0 | 1 |+-----+-----+ +-----+-----+-----+d | 2 | 1 |+-----+-----+所以总体的递推公式为:
dp[i][j]=min(dp[i−1][j]+1,dp[i][j]=dp[i−1][j−1]+1,dp[i][j]=dp[i][j−1]+1)dp[i][j] = min({dp[i-1][j]+1, dp[i][j] = dp[i-1][j-1]+1,dp[i][j] = dp[i][j-1]+1})dp[i][j]=min(dp[i−1][j]+1,dp[i][j]=dp[i−1][j−1]+1,dp[i][j]=dp[i][j−1]+1) -
初始化
dp[i][0]dp[i][0]dp[i][0]代表word1要和空字符相等需要多少次删除操作,显然为i;同理,dp[0][j]dp[0][j]dp[0][j]代表word2要和空字符 相等需要多少次删除操作,显然为j,所以初始化操作如下:for(int i = 0; i <= word1.size(); i++) dp[i][0] = i; for(int j = 0; j <= word2.size(); j++) dp[0][j] = j; -
遍历顺序
显然遍历是从上到下,从左到右
代码:
class Solution {
public:int minDistance(string word1, string word2) {vector<vector<int>>dp(word1.size() + 1, vector<int>(word2.size()+ 1, 0));for(int i = 0; i <= word1.size(); i++) dp[i][0] = i;for(int j = 0; j <= word2.size(); j++) dp[0][j] = j;for(int i = 1; i <= word1.size(); i++){for(int j = 1; j <= word2.size(); j++){if(word1[i - 1] == word2[j - 1])dp[i][j] = dp[i - 1][j -1];elsedp[i][j] = min({dp[i - 1][j] + 1, dp[i][j - 1] + 1, dp[i - 1][j - 1] + 1});}}return dp[word1.size()][word2.size()];}
};
总结
重点要理解word1添加元素相当于word2删除元素
今日总结:
学习了编辑距离问题。
相关文章:

代码随想录算法训练营第五十六天|583. 两个字符串的删除操作、72. 编辑距离
LeetCode 583 两个字符串的删除操作 题目链接:https://leetcode.cn/problems/delete-operation-for-two-strings/ 思路: 方法一:两个子串同时删除元素 dp数组的含义 dp[i][j]dp[i][j]dp[i][j]代表以i-1为结尾的字符串word1,和以j-1位结…...
【ArchLinux】【KDE】Archlinux的安装与使用
文章目录开头前言所需环境演示环境相关链接安装教程在Windows环境下制作启动盘进入ArchLinux Live环境安装为硬盘分区如何新建分区?分区表格式化分区分区完成,开始安装挂载分区切换镜像源安装基本系统设置将Live环境(当前)挂载信息…...

Go语言精修(尚硅谷笔记)第六章
六、函数、包和错误处理 6.1 函数概念 不用函数的弊端 1)写法可以完成功能, 但是代码冗余 2 ) 同时不利于代码维护 概念:为完成某一功能的程序指令(语句)的集合,称为函数。 在Go中,函数分为: 自定义函数、系统函数 基本语法 //函数的基本语法 fu…...

Photoshop的功能
Photoshop是一款功能强大的图片编辑软件,它提供了数百种不同的工具和特效,让您可以编辑图片、创建图形和设计网页等。 以下是Photoshop的一些主要功能: 1.图层:Photoshop允许您创建多个图层,让您可以在每一个图层上进…...

C++初阶——内存管理
目录 1. C/C内存分布 2. C语言中动态内存管理方式:malloc/calloc/realloc/free 3. C内存管理方式 3.1 new/delete操作内置类型 3.2 new和delete操作自定义类型 4. operator new与operator delete函数 重要 4.1 operator new与operator delete函数(…...
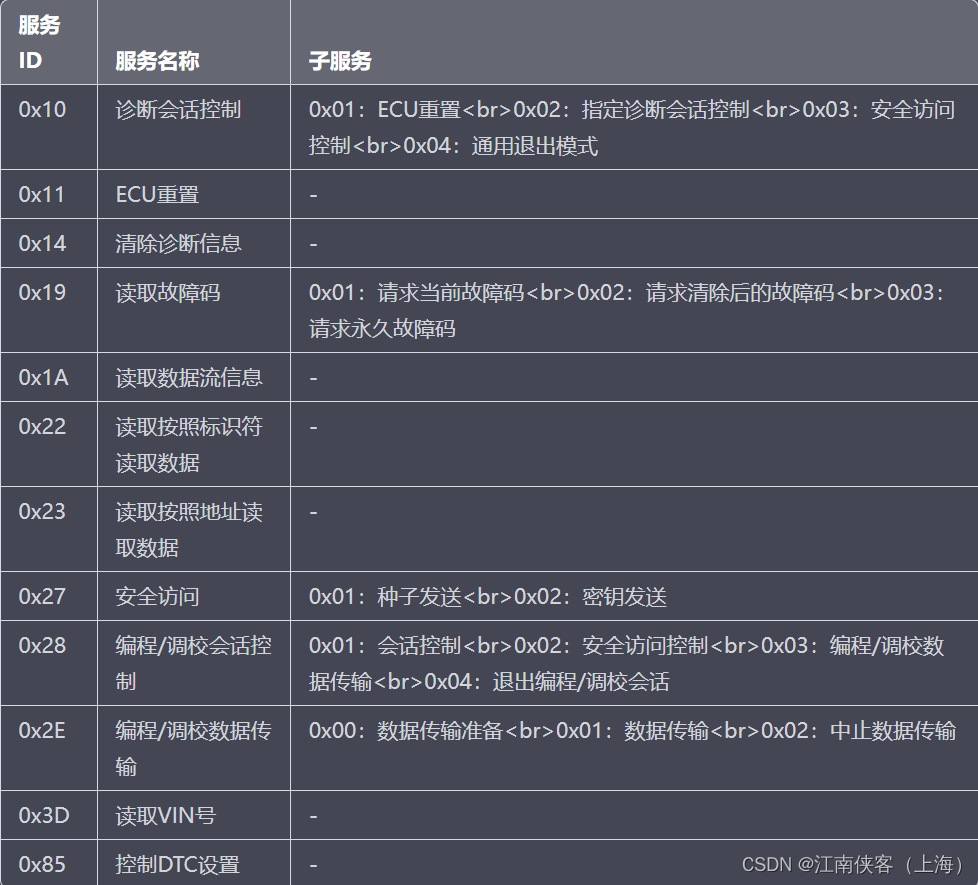
uds服务汇总
还有一些服务列举在下面: RequestDownload(服务ID为0x34)和RequestUpload(服务ID为0x35):这两个服务用于在ECU和诊断器之间进行数据传输。通过 RequestDownload服务,诊断器可以请求ECU接收一些数…...

【深度学习】2023李宏毅homework1作业一代码详解
研一刚入门深度学习的小白一枚,想记录自己学习代码的经过,理解每行代码的意思,这样整理方便日后复习也方便理清自己的思路。感觉每天时间都不够用了!!加油啦。 第一部分:导入模块 导入各个模块࿰…...
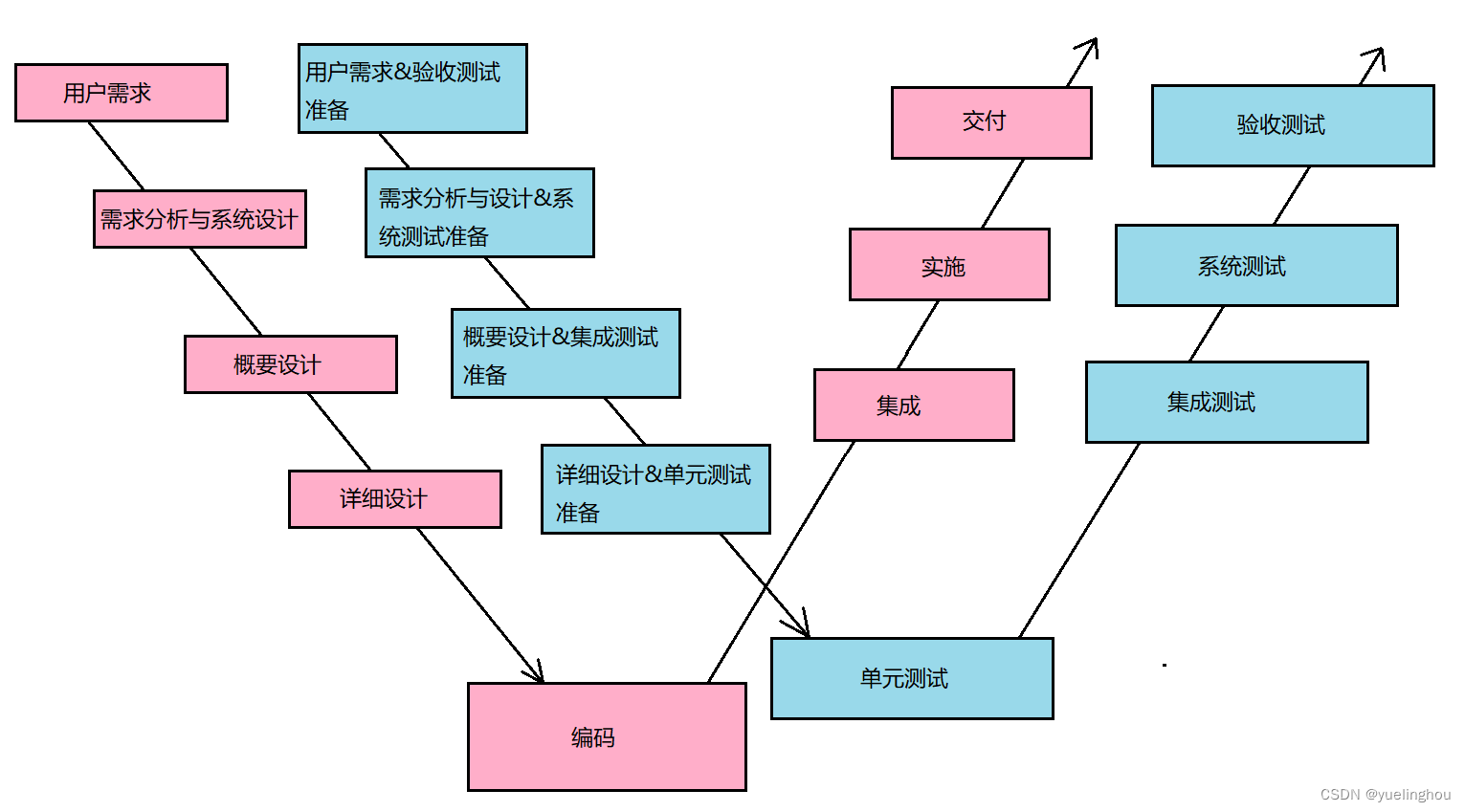
【软件测试】基础知识第二篇
文章目录一. 开发模型1. 瀑布模型2. 螺旋模型3. 增量和迭代模型3.1 增量模型3.2 迭代模型3.3 增量和迭代模型的区别4. 敏捷模型4.1 敏捷宣言4.2 scrum模型二. 开发模型V 模型W 模型一. 开发模型 1. 瀑布模型 瀑布模型在软件工程中占有重要地位,是所有其他模型的基…...

Java中File类以及初步认识流
1、File类操作文件或目录属性 (1)在Java程序中通过使用java.io包提供的一些接口和类,对计算机中的文件进行基本的操作,包括对文件和目录属性的操作、对文件读写的操作; (2)File对象既可以表示…...
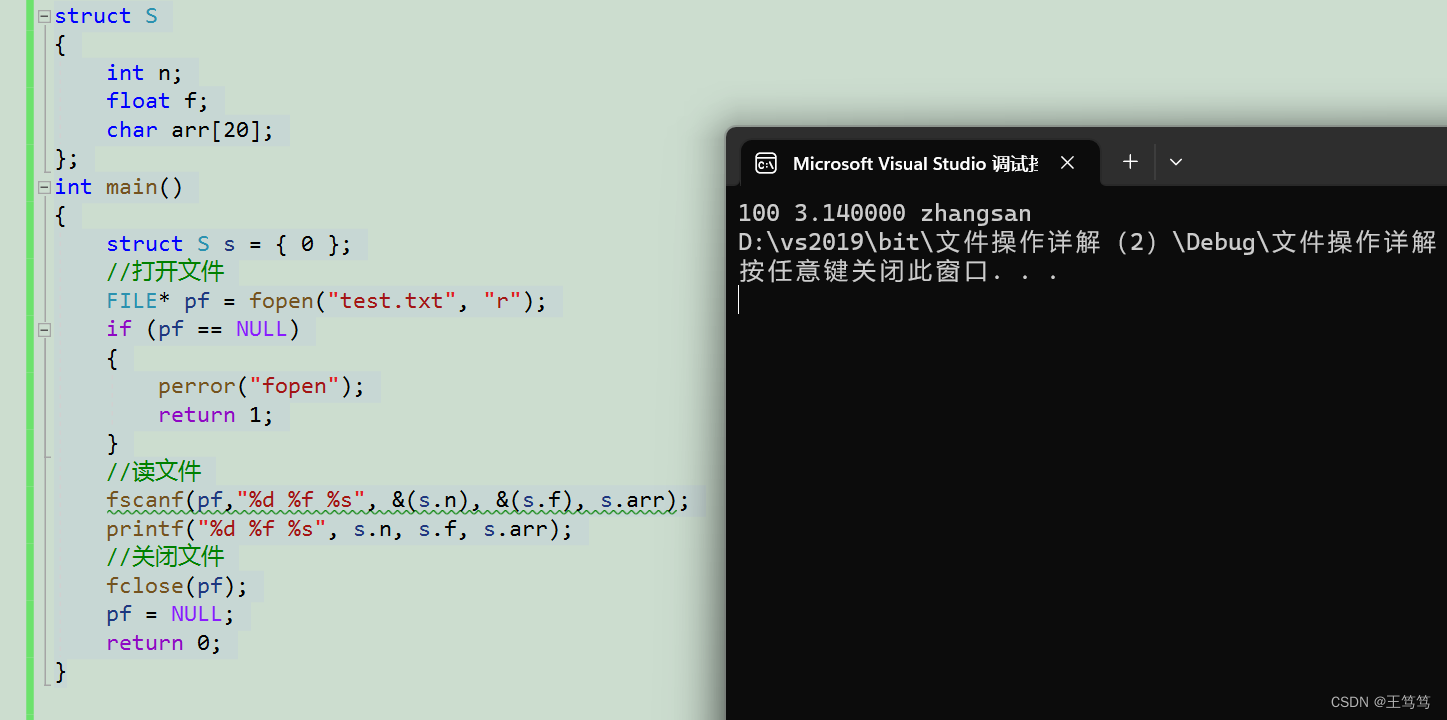
【C语言】文件操作详细讲解
本章要分享的内容是C语言中文件操作的内容,为了方便大家学习,目录如下 目录 1.为什么要使用文件 2.什么是文件 2.1 程序文件 2.2 数据文件 2.3 文件名 3.文件的打开和关闭 3.1文件指针 3.2打开和关闭 4.文件的顺序读写 4.1顺序读写函数介绍…...

爱奇艺万能联播使用教程
众所周知,爱奇艺是百度旗下的一款产品,所以今天用爱奇艺万能联播的方法实现下载百度网盘,并没有破解百度网盘,是官方正版下载渠道。软件是官方版本,大家双击安装即可。 安装完成以后,在软件中就有了“访问网…...
真题讲解-软件设计(三十七)
数据流图DFD(真题讲解)-软件设计(三十六)https://blog.csdn.net/ke1ying/article/details/129803164 在网络安全管理中,加强内防内控可采取的策略是? 终端访问权限,防止合法终端越权访问。加强…...

Android 上的协程(第一部分):了解背景
本系列文章 Android 上的协程(第一部分):了解背景 Android 上的协程(第二部分):入门 Android上的协程 (第三部分): 实际应用 Android 上的协程(第一部分):了解背景 这篇…...

【H3C】VRRP2 及Vrrp3基本原理 华为同用
文章目录VRRP2基本概念报文格式主备选举规则(优先级)0和255双Master原因VRRP认证VRRP状态机抢占模式VRRP主备切换状态项目场景VRRP3H3C参考致谢VRRP2 基本概念 VRRP路由器(VRRP Router):运行VRRP的设备,它…...
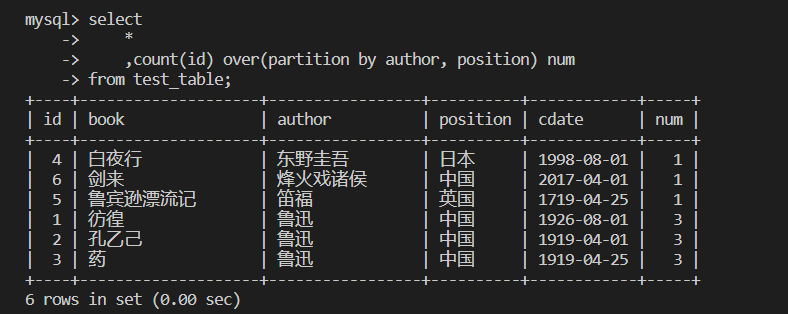
【数据库】SQL语法
目录 1. 常用数据类型 2. 约束 3. 数据库操作 4. 数据表操作 查看表 创建表格 添加数据 删除数据 修改数据 单表查询数据 多表查询数据 模糊查询 关联查询 连接查询 数据查询的执行顺序 4. 内置函数 1. 常用数据类型 整型:int浮点型:flo…...
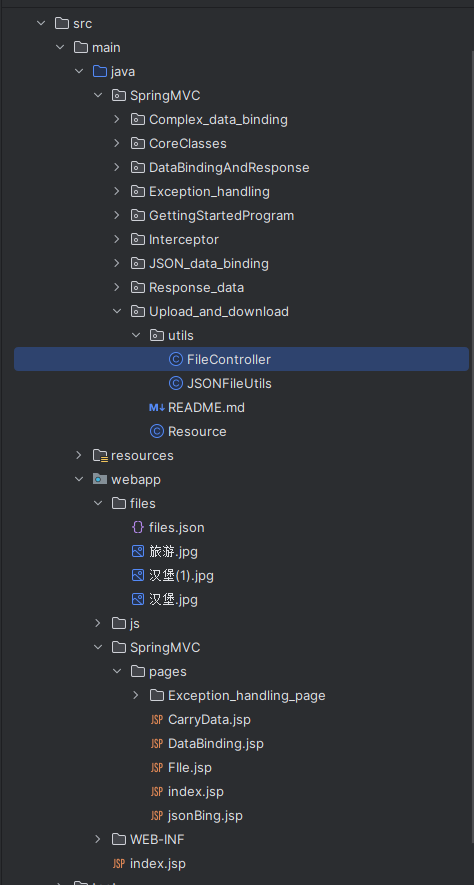
JavaEE简单示例——文件的上传和下载
文件的上传和下载的实现原理的简单介绍 表单的构成 首先,我们先来介绍我们的需要用到的表单,在这个表单中,首先值得我们注意的就是,在type为file的input标签中.这个控件是我们主要用来选择上传的文件的, 除此之外,我们要想实现文件的上传,还需要将method的属性的值设置为post…...
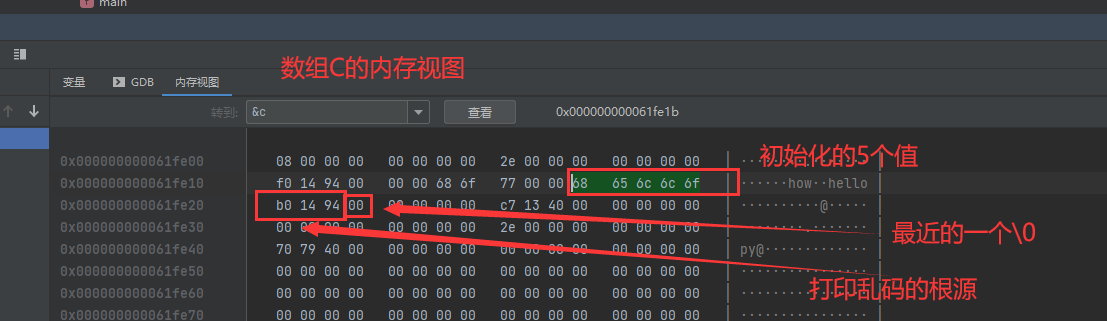
【C语言督学训练营 第五天】数组字符串相关知识
文章目录前言一、数组的定义1.一维数组①.如何定义②.声明规则③.内存分布④.初始化方法2.二维数组3.高维数组二、访问数组元素相关问题1.访问越界2.数组的传递三、Scanf与字符数组1.字符数组初始化2.scanf读取字符四、字符数组相关函数前言 今天的C语言训练营没有安排高维数组…...
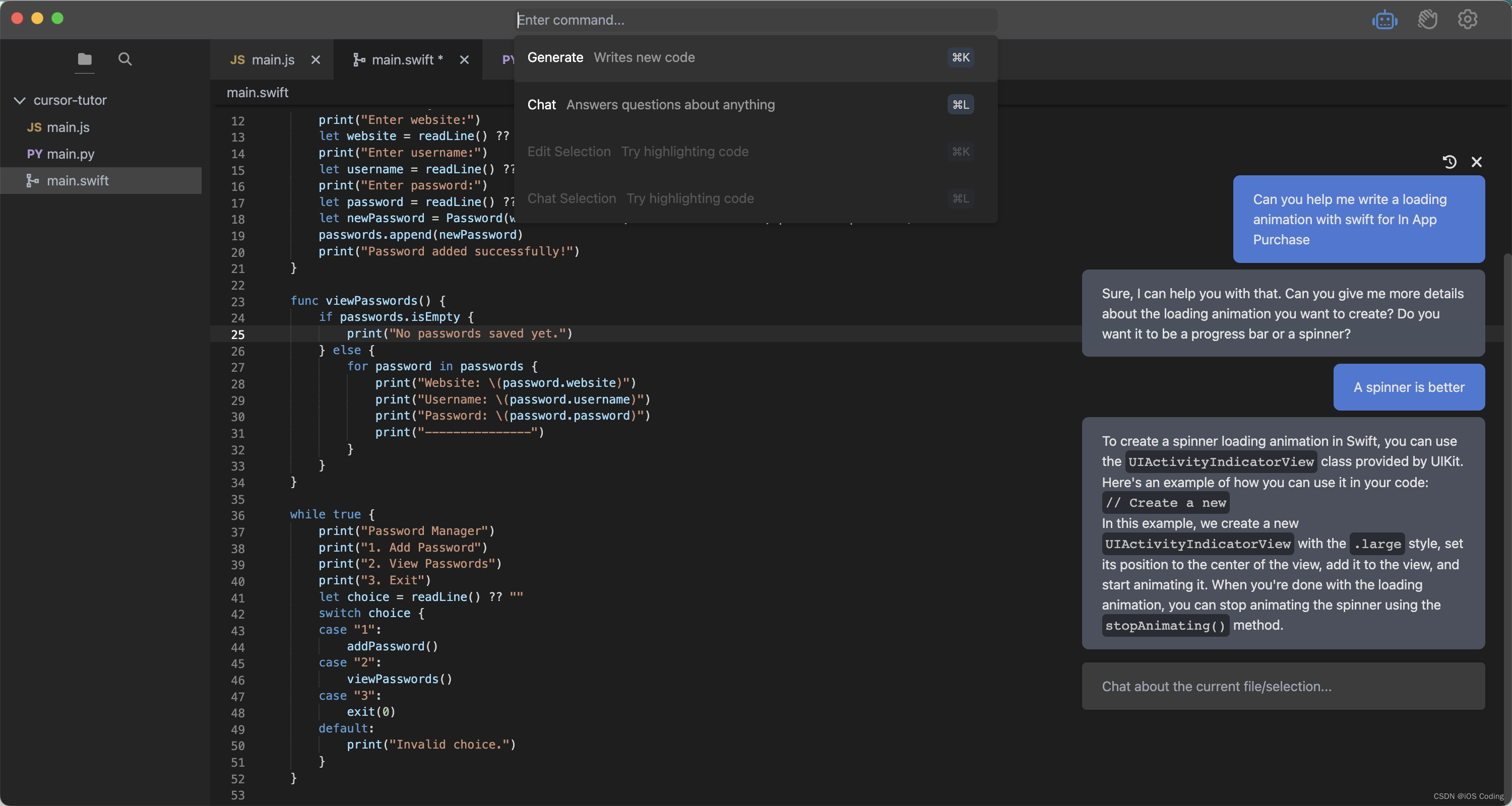
GPT-4 免费体验方法
POE 在Quora上非常受欢迎的手机聊天机器人Poe App已经集成ChatGPT助手!除了最初集成的三个聊天机器人Sage、Claude和Dragonfly外,Poe现在还加入了第四位ChatGPT。由于使用了ChatGPT API,因此Poe拥有真正的ChatGPT。 现在更是第一批集成了GP…...

中断-屏蔽位
1.中断控制器(PIC:适用于单处理器、APIC) 1.定义 中断控制器可以看作是中断服务的代理,外设五花八门,如果没有一个中断的代理,外设想要给cpu发送中断信号来处理中断。那么只能是外设连接在cpu引脚上,由于cpu引脚很宝贵,所以不可能拿出那么多引脚来供外设连接,所以就有…...

【洛谷P1636】 Einstein学画画
题目描述:Einstein 学起了画画。此人比较懒~~,他希望用最少的笔画画出一张画……给定一个无向图,包含 n 个顶点(编号 1∼n),m 条边,求最少用多少笔可以画出图中所有的边。输入格式第一行两个整数…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

【论文笔记】若干矿井粉尘检测算法概述
总的来说,传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度,通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...
