(转载)智能指针shared_ptr从C++11到C++20
shared_ptr和动态数组 - apocelipes - 博客园 (cnblogs.com)
template<typename T>
std::shared_ptr<T> make_shared_array(size_t size)
{
return std::shared_ptr<T>(new T[size],std::default_delete<T[]>());
}
std::shared_ptr<int> p8 = make_shared_array<int>(10);
std::shared_ptr<char> p9 = make_shared_array<char>(10);
相关文章:
智能指针shared_ptr从C++11到C++20)
(转载)智能指针shared_ptr从C++11到C++20
shared_ptr和动态数组 - apocelipes - 博客园 (cnblogs.com) template<typename T> std::shared_ptr<T> make_shared_array(size_t size) { return std::shared_ptr<T>(new T[size],std::default_delete<T[]>()); } std::shar…...
Ubuntu 上安装 Miniconda
一、下载 Miniconda 打开终端。访问 Anaconda 官方仓库下载页面https://repo.anaconda.com/miniconda/选择Miniconda3-py310_24.7.1-0-Linux-x86_64.sh,进行下载。文件名当中的py310_24.7.1表示,在 conda 的默认的 base 环境中的 Python 版本是3.10&…...
【Vue系列五】—Vue学习历程的知识分享!
前言 本篇文章讲述前端工程化从模块化到如今的脚手架的发展,以及Webpack、Vue脚手架的详解! 一、模块化 模块化就是把单独的功能封装到模块(文件)中,模块之间相互隔离,但可以通过特定的接口公开内部成员…...

CaLM 因果推理评测体系:如何让大模型更贴近人类认知水平?
CaLM 是什么 CaLM(Causal Evaluation of Language Models,以下简称“CaLM”)是上海人工智能实验室联合同济大学、上海交通大学、北京大学及商汤科技发布首个大模型因果推理开放评测体系及开放平台。首次从因果推理角度提出评估框架ÿ…...

深入探索卷积神经网络(CNN)
深入探索卷积神经网络(CNN) 前言图像的数字表示灰度图像RGB图像 卷积神经网络(CNN)的架构基本组件卷积操作填充(Padding)步幅(Strides) 多通道图像的卷积池化层全连接层 CNN与全连接…...

【C++篇】手撕 C++ string 类:从零实现到深入剖析的模拟之路
文章目录 C string 类的模拟实现:从构造到高级操作前言第一章:为什么要手写 C string 类?1.1 理由与价值 第二章:实现一个简单的 string 类2.1 基本构造与析构2.1.1 示例代码:基础的 string 类实现2.1.2 解读代码 2.2 …...

毕业设计选题:基于ssm+vue+uniapp的校园失物招领小程序
开发语言:Java框架:ssmuniappJDK版本:JDK1.8服务器:tomcat7数据库:mysql 5.7(一定要5.7版本)数据库工具:Navicat11开发软件:eclipse/myeclipse/ideaMaven包:M…...

[系统设计总结] - Proximity Service算法介绍
问题描述 Proximity Service广泛应用于各种地图相关的服务中比如外卖,大众点评,Uber打车,Google地图中,其中比较关键的是我们根据用户的位置来快速找到附近的餐厅,司机,外卖员也就是就近查询算法。 主流的…...

变压吸附制氧机的应用范围
变压吸附制氧机是一种利用变压吸附技术从空气中分离出氧气的设备。该技术通过吸附剂在不同压力下的吸附与解吸性能,实现了氧气的有效分离和纯化。 工业领域 在工业领域,变压吸附制氧机同样具有广泛的应用。首先,钢铁企业在生产过程中需要大量…...

MATLAB绘图基础8:双变量图形绘制
参考书:《 M A T L A B {\rm MATLAB} MATLAB与学术图表绘制》(关东升)。 8.双变量图形绘制 8.1 散点图 散点图用于显示两个变量间的关系,每个数据点在图上表示为一个点,一个变量在 X {\rm X} X轴,一个变量在 Y {\rm Y} Y轴&#…...

Appium高级话题:混合应用与原生应用测试策略
Appium高级话题:混合应用与原生应用测试策略 在移动应用开发领域,混合应用与原生应用各有千秋,但它们的测试策略却大相径庭。本文旨在深入探讨这两种应用类型的测试挑战,并介绍如何利用自动化测试软件ItBuilder高效解决这些问题&…...

windows源码安装protobuf,opencv,ncnn
安装笔记 cmake 在windows可以使用-G"MinGW Makefiles" 搭配make使用,install出来的lib文件时.a结尾的,适合linux下面使用。所以在windows上若无需求使用-G"NMake Makefiles" 搭配nmake。 但是windows上使用-G"NMake Makefil…...

MicroPython 怎么搭建工程代码
在MicroPython中搭建工程代码可以遵循以下步骤: 1. 准备工作 安装MicroPython固件:确保已经将MicroPython烧录到ESP32开发板中。准备开发环境: 可以使用文本编辑器(如VS Code、Thonny、uPyCraft等)来编写代码。 2.…...

Android studio安装问题及解决方案
Android studio安装问题及解决方案 gradle已经安装好了,但是每次就是找不到gradle的位置,每次要重新下载,很慢,每次都不成功 我尝试用安装android studio时自带的卸载程序,卸载android studio,然后重新下…...
)
前端面试题(二)
6. 深入 JavaScript this 关键字的指向是什么? this 的指向是在函数执行时决定的。默认情况下,非严格模式下 this 指向全局对象(浏览器中为 window),严格模式下 this 为 undefined。在对象方法中,this 通常…...

【C++】stack和queue的使用及模拟实现
stack就是栈的意思,这个结构遵循后进先出(LIFO)的原则,可以将栈想象为一个子弹夹,先进去的子弹后出来。 queue就是队列的意思,这个结构遵循先进先出(FIFO)的原则,可以将对列想象成我们排队买饭的场景,先排…...

MongoDB解说
MongoDB 是一个流行的开源 NoSQL 数据库,它使用了一种被称为文档存储的数据库模型。 与传统的关系型数据库管理系统(RDBMS)不同,MongoDB 不使用表格来存储数据,而是使用了一种更为灵活的格式——JSON 样式的文档。 这…...

问:JAVA中唤醒阻塞的线程有哪些?
在Java中,唤醒阻塞线程的方法有多种,以下是常见的线程唤醒方法。 唤醒方法 使用notify()和notifyAll()方法 synchronized (obj) {obj.notify(); // 唤醒单个等待线程// obj.notifyAll(); // 唤醒所有等待线程 }使用interrupt()方法 Thread thread n…...
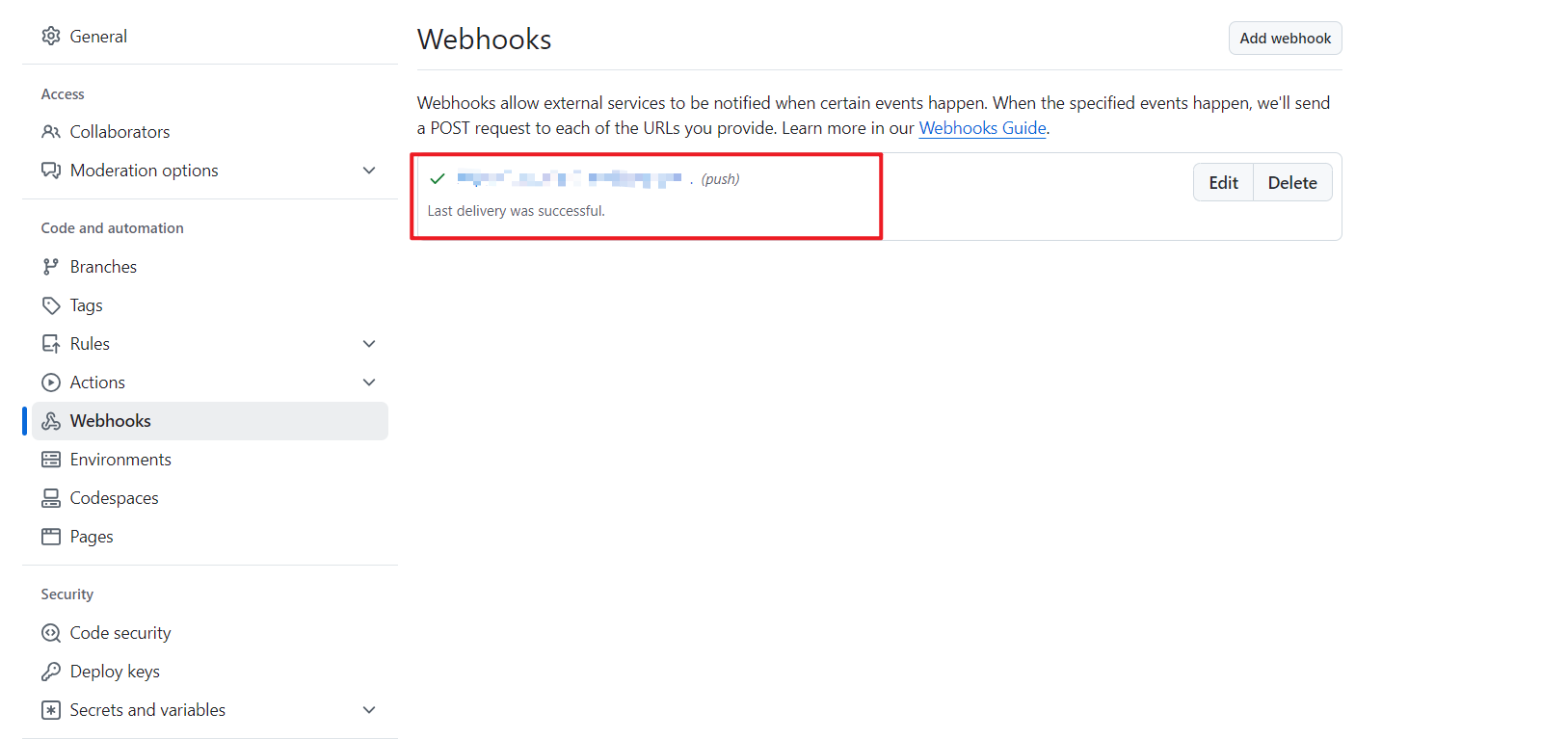
Github Webhook触发Jenkins自动构建
1.功能说明 Github Webhook可以触发Jenkins自动构建,通过配置Github Webhook,每次代码变更之后(例如push操作),Webhook会自动通知Jenkins服务器,Jenkins会自动执行预定义的构建任务(如Jenkins …...

ESP32-WROOM-32 [创建AP站点-客户端-TCP透传]
简介 基于ESP32-WROOM-32 开篇(刚买), 本篇讲的是基于固件 ESP32-WROOM-32-AT-V3.4.0.0(内含用户指南, 有AT指令说明)的TCP透传设置与使用 设备连接 TTL转USB线, 接ESP32 板 的 GND,RX2, TX2 指令介绍 注意,下面指…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...
