【代码随想录训练营第42期 Day60打卡 - 图论Part10 - Bellman_ford算法系列运用
目录
一、Bellman_ford算法的应用
二、题目与题解
题目一:卡码网 94. 城市间货物运输 I
题目链接
题解:队列优化Bellman-Ford算法(SPFA)
题目二:卡码网 95. 城市间货物运输 II
题目链接
题解: 队列优化Bellman-Ford算法(SPFA)
题目三:卡码网 96. 城市间货物运输 III
题目链接
题解: Bellman-Ford算法
三、小结
一、Bellman_ford算法的应用
Bellman-Ford算法是一种用于解决单源最短路径问题的算法,它能够处理含有负权边的图,并且能够检测图中是否存在负权回路。
其应用一般分为以下几个方面:
1、最短路径问题:在图论中,Bellman - Ford算法是解决单源最短路径问题的有效工具。它可以找到从一个顶点到所有其他顶点的最短路径。
2、负权边:与Dijkstra算法不同,Bellman - Ford算法能够处理含有负权边的图。这意味着它可以解决那些包含负权重边的图的最短路径问题。
3、运输问题:在运输问题中,需要找到从一个供应点(源)到多个需求点(汇)的最小成本运输路径。Bellman - Ford算法可以用来解决这个问题,尤其是在存在负权边的情况下。
4、流网络问题:在流网络中,Bellman - Ford算法可以用来找到从一个节点到另一个节点的最大流。这是因为在某些流网络问题中,边的权重可以表示为流量的限制。
5、网络流问题:在网络流问题中,Bellman - Ford算法可以用来找到从一个源点到汇点的最小费用流。这涉及到在网络中传输物质或信息,并需要最小化成本。
6、动态最短路径问题:在某些情况下,图的结构可能会发生变化,例如添加或删除边。Bellman - Ford算法可以用来动态地更新最短路径信息。
7、多源最短路径问题:Bellman - Ford算法可以扩展为解决多源最短路径问题,即找到多个源点到其他所有顶点的最短路径。
8、网络路由问题:在网络路由问题中,需要找到从一个网络节点到另一个网络节点的最佳路径。Bellman - Ford算法可以用来解决包含负权边的网络路由问题。
Bellman-Ford算法的主要优点是它能够处理负权边,这是其他最短路径算法(如Dijkstra算法)所不能做到的。然而,它的主要缺点是时间复杂度较高,为O(VE),其中V是顶点数,E是边数。在实际应用中,如果图中的边数远大于顶点数,Bellman-Ford算法可能不如Dijkstra算法高效。
二、题目与题解
题目一:卡码网 94. 城市间货物运输 I
题目链接
94. 城市间货物运输 I (kamacoder.com)
题目描述
某国为促进城市间经济交流,决定对货物运输提供补贴。共有 n 个编号为 1 到 n 的城市,通过道路网络连接,网络中的道路仅允许从某个城市单向通行到另一个城市,不能反向通行。
网络中的道路都有各自的运输成本和政府补贴,道路的权值计算方式为:运输成本 - 政府补贴。权值为正表示扣除了政府补贴后运输货物仍需支付的费用;权值为负则表示政府的补贴超过了支出的运输成本,实际表现为运输过程中还能赚取一定的收益。
请找出从城市 1 到城市 n 的所有可能路径中,综合政府补贴后的最低运输成本。如果最低运输成本是一个负数,它表示在遵循最优路径的情况下,运输过程中反而能够实现盈利。
城市 1 到城市 n 之间可能会出现没有路径的情况,同时保证道路网络中不存在任何负权回路。
输入描述
第一行包含两个正整数,第一个正整数 n 表示该国一共有 n 个城市,第二个整数 m 表示这些城市中共有 m 条道路。
接下来为 m 行,每行包括三个整数,s、t 和 v,表示 s 号城市运输货物到达 t 号城市,道路权值为 v (单向图)。
输出描述
如果能够从城市 1 到连通到城市 n, 请输出一个整数,表示运输成本。如果该整数是负数,则表示实现了盈利。如果从城市 1 没有路径可达城市 n,请输出 "unconnected"。
输入示例
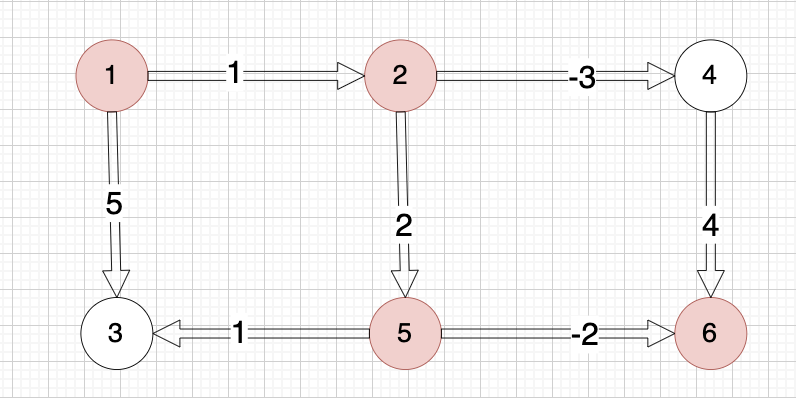
6 7 5 6 -2 1 2 1 5 3 1 2 5 2 2 4 -3 4 6 4 1 3 5输出示例
1提示信息
示例中最佳路径是从 1 -> 2 -> 5 -> 6,路上的权值分别为 1 2 -2,最终的最低运输成本为 1 + 2 + (-2) = 1。
示例 2:
4 2
1 2 -1
3 4 -1在此示例中,无法找到一条路径从 1 通往 4,所以此时应该输出 "unconnected"。
数据范围:
1 <= n <= 1000;
1 <= m <= 10000;-100 <= v <= 100;
题解:队列优化Bellman-Ford算法(SPFA)
这题在昨天的打卡中已经有提到一般实现的Bellman-Ford算法,今天这里将用队列优化后的Bellman-Ford算法进行实现。
Bellman - Ford算法实现:
1、创建一个队列q,先将源点加入队列。
2、进入循环,当队列非空时,继续执行以下操作:
(1)从队列中取出队头节点node;
(2)标记该节点已从队列中取出;
(3)遍历当前节点的所有邻接边:
a.如果通过当前节点到达邻接节点的距离更短,则更新最短距离;
b.如果邻接节点不在队列中,则将其加入队列,并标记为已加入。
完整代码如下:
#include <bits/stdc++.h>
using namespace std;struct Edge // 邻接表
{int to; // 边的指向节点(边链接的节点 -- 邻接节点)int val; // 边的权重Edge(int t, int w) : to(t), val(w) {} // 构造函数,初始化边的指向节点和权重
};int main()
{int n, m, p1, p2, val;cin >> n >> m;vector<list<Edge>> grid(n + 1); // 创建一个邻接表,存储图的信息,大小为n+1,因为节点编号从1开始vector<bool> inQueue(n + 1); // 用于标记节点是否已经在队列中(避免重复添加)// 将所有边保存起来,构建邻接表for (int i = 0; i < m; i++){cin >> p1 >> p2 >> val;grid[p1].push_back(Edge(p2, val)); // p1指向p2,边权重为val,将边添加到邻接表中}int start = 1; // 起点int end = n; // 终点vector<int> minDist(n + 1, INT_MAX); // 初始化最短距离数组,所有节点到源点的最短距离初始为无穷大minDist[start] = 0; // (除外)源点到自己的距离为0// 队列优化Bellman-Ford算法queue<int> q;q.push(start); //先将起点加入队列while (!q.empty()){int node = q.front(); // 取出队头节点 -- 作为后续邻接边的起始节点q.pop();inQueue[node] = false; // 标记该节点已从队列中取出// 遍历当前节点的所有邻接边 -- 当前节点即是这些边的起始节点for (Edge edge : grid[node]){int from = node;int to = edge.to;int value = edge.val;if (minDist[to] > minDist[from] + value) // 开始松弛:如果通过当前节点到达邻接节点to的距离更短,则更新邻接节点to到源点的最短距离{ minDist[to] = minDist[from] + value;if (inQueue[to] == false) // 如果该节点不在队列中,则加入队列,并标记为已加入{ q.push(to);inQueue[to] = true;}}}}if (minDist[end] == INT_MAX)cout << "unconnected" << endl; // 不能到达终点elsecout << minDist[end] << endl; // 到达终点最短路径
}题目二:卡码网 95. 城市间货物运输 II
题目链接
95. 城市间货物运输 II (kamacoder.com)
题目描述
某国为促进城市间经济交流,决定对货物运输提供补贴。共有 n 个编号为 1 到 n 的城市,通过道路网络连接,网络中的道路仅允许从某个城市单向通行到另一个城市,不能反向通行。
网络中的道路都有各自的运输成本和政府补贴,道路的权值计算方式为:运输成本 - 政府补贴。权值为正表示扣除了政府补贴后运输货物仍需支付的费用;权值为负则表示政府的补贴超过了支出的运输成本,实际表现为运输过程中还能赚取一定的收益。
然而,在评估从城市 1 到城市 n 的所有可能路径中综合政府补贴后的最低运输成本时,存在一种情况:图中可能出现负权回路。负权回路是指一系列道路的总权值为负,这样的回路使得通过反复经过回路中的道路,理论上可以无限地减少总成本或无限地增加总收益。为了避免货物运输商采用负权回路这种情况无限的赚取政府补贴,算法还需检测这种特殊情况。
请找出从城市 1 到城市 n 的所有可能路径中,综合政府补贴后的最低运输成本。同时能够检测并适当处理负权回路的存在。
城市 1 到城市 n 之间可能会出现没有路径的情况
输入描述
第一行包含两个正整数,第一个正整数 n 表示该国一共有 n 个城市,第二个整数 m 表示这些城市中共有 m 条道路。
接下来为 m 行,每行包括三个整数,s、t 和 v,表示 s 号城市运输货物到达 t 号城市,道路权值为 v。
输出描述
如果没有发现负权回路,则输出一个整数,表示从城市
1到城市n的最低运输成本(包括政府补贴)。如果该整数是负数,则表示实现了盈利。如果发现了负权回路的存在,则输出 "circle"。如果从城市 1 无法到达城市 n,则输出 "unconnected"。输入示例
4 4 1 2 -1 2 3 1 3 1 -1 3 4 1输出示例
circle提示信息
路径中存在负权回路,从 1 -> 2 -> 3 -> 1,总权值为 -1,理论上货物运输商可以在该回路无限循环赚取政府补贴,所以输出 "circle" 表示已经检测出了该种情况。
数据范围:
1 <= n <= 1000;
1 <= m <= 10000;-100 <= v <= 100;
题解: 队列优化Bellman-Ford算法(SPFA)
这题是bellman-ford算法判断负权回路的应用。
和上一题相比较,区别也就在于对负权回路的判断,其余思路保持一致。
故这里有一个关键,即如何判断负权回路:
我们用计数器记录每个节点加入队列的次数。如果某个节点的计数器达到了n(即所有节点的数量),那么这个节点在经过V-1次松弛操作后,仍然可以通过负权边继续进行松弛。这违反了Bellman-Ford算法的假设,即在V-1次松弛操作后,最短路径应该已经被找到。因此,可以判断出图中存在负权回路。
完整代码如下:
#include <bits/stdc++.h>
using namespace std;struct Edge // 邻接表
{int to; // 边的指向节点(边链接的节点 -- 邻接节点)int val; // 边的权重Edge(int t, int w) : to(t), val(w) {} // 构造函数,初始化边的指向节点和权重
};int main()
{int n, m, p1, p2, val;cin >> n >> m;vector<list<Edge>> grid(n + 1); // 创建一个邻接表,存储图的信息,大小为n+1,因为节点编号从1开始vector<bool> inQueue(n + 1); // 用于标记节点是否已经在队列中(避免重复添加)// 将所有边保存起来,构建邻接表for (int i = 0; i < m; i++){cin >> p1 >> p2 >> val;grid[p1].push_back(Edge(p2, val)); // p1指向p2,边权重为val,将边添加到邻接表中}int start = 1; // 起点(源点)int end = n; // 终点vector<int> minDist(n + 1, INT_MAX);minDist[start] = 0;queue<int> q;q.push(start); // 队列里放入起点vector<int> count(n + 1, 0); // 创建一个计数器数组,用于记录每个节点加入队列的次数count[start]++; // 刚放入一次起点,计数+1bool flag = false; // 设置一个标志,用于标记是否找到了负权回路,初始化为falsewhile (!q.empty()){int node = q.front();q.pop();for (Edge edge : grid[node]){int from = node;int to = edge.to;int value = edge.val;if (minDist[to] > minDist[from] + value) // 开始松弛:如果通过当前节点到达邻接节点to的距离更短,则更新邻接节点to到源点的最短距{minDist[to] = minDist[from] + value;q.push(to);count[to]++;if (count[to] == n) // 关键:如果加入队列次数超过n-1次,就说明该图与负权回路{flag = true;while (!q.empty())q.pop();break;}}}}if (flag) // 如果存在负权回路,输出"circle"cout << "circle" << endl;else if (minDist[end] == INT_MAX)cout << "unconnected" << endl;elsecout << minDist[end] << endl;
}
题目三:卡码网 96. 城市间货物运输 III
题目链接
96. 城市间货物运输 III (kamacoder.com)
题目描述
某国为促进城市间经济交流,决定对货物运输提供补贴。共有 n 个编号为 1 到 n 的城市,通过道路网络连接,网络中的道路仅允许从某个城市单向通行到另一个城市,不能反向通行。
网络中的道路都有各自的运输成本和政府补贴,道路的权值计算方式为:运输成本 - 政府补贴。权值为正表示扣除了政府补贴后运输货物仍需支付的费用;权值为负则表示政府的补贴超过了支出的运输成本,实际表现为运输过程中还能赚取一定的收益。
请计算在最多经过 k 个城市的条件下,从城市 src 到城市 dst 的最低运输成本。
输入描述
第一行包含两个正整数,第一个正整数 n 表示该国一共有 n 个城市,第二个整数 m 表示这些城市中共有 m 条道路。
接下来为 m 行,每行包括三个整数,s、t 和 v,表示 s 号城市运输货物到达 t 号城市,道路权值为 v。
最后一行包含三个正整数,src、dst、和 k,src 和 dst 为城市编号,从 src 到 dst 经过的城市数量限制。
输出描述
输出一个整数,表示从城市 src 到城市 dst 的最低运输成本,如果无法在给定经过城市数量限制下找到从 src 到 dst 的路径,则输出 "unreachable",表示不存在符合条件的运输方案。
输入示例
6 7 1 2 1 2 4 -3 2 5 2 1 3 5 3 5 1 4 6 4 5 6 -2 2 6 1输出示例
0提示信息
从 2 -> 5 -> 6 中转一站,运输成本为 0。
1 <= n <= 1000;
1 <= m <= 10000;
-100 <= v <= 100;
题解: Bellman-Ford算法
这题是bellman_ford算法解决单源有限最短路问题的应用。
这题Bellman - Ford算法实现的关键在于:
使用minDist_copy来保留上一次迭代的结果,从而避免重复计算和比较,提高算法的效率。如果在当前迭代中没有发现新的更短路径,那么在接下来的迭代中,可以只检查minDist_copy是否已经包含了一条更短的路径,如果没有,那么就不需要更新minDist数组。
通过进行k + 1次松弛操作,每次迭代开始时,将当前的minDist数组的内容复制到minDist_copy中。 遍历所有边,进行松弛操作。如果在松弛过程中发现通过某个节点到达某个邻接节点的距离更短,则更新最短距离。
#include <bits/stdc++.h>
using namespace std;int main()
{int src, dst, k, p1, p2, val, m, n; // 起点src,终点dst,松弛次数kcin >> n >> m;vector<vector<int>> grid; // 创建一个二维向量grid,用于存储图的信息:每个元素都是一条边(包含起始点,终止点,权值)// 读取所有边,并添加到grid中for (int i = 0; i < m; i++){cin >> p1 >> p2 >> val;grid.push_back({p1, p2, val});}cin >> src >> dst >> k;vector<int> minDist(n + 1, INT_MAX); // 用于存储从起点到每个节点的最短距离,都初始化为最大值INT_MAXminDist[src] = 0; // 起点除外,起点到本身的距离为0vector<int> minDist_copy(n + 1); // 用来记录上一次遍历的结果// 进行k次松弛操作for (int i = 1; i <= k + 1; i++){minDist_copy = minDist; // 将上一次计算的结果赋值给minDist_copy:即将当前的minDist数组的内容复制到一个新的数组minDist_copy中// 遍历所有边,进行松弛操作for (vector<int> &side : grid){int from = side[0];int to = side[1];int price = side[2];// 注意使用 minDist_copy 来计算 minDistif (minDist_copy[from] != INT_MAX && minDist[to] > minDist_copy[from] + price){minDist[to] = minDist_copy[from] + price;}}}if (minDist[dst] == INT_MAX) // 不能到达终点cout << "unreachable" << endl;elsecout << minDist[dst] << endl; // 到达终点最短路径
}
三、小结
相关文章:
【代码随想录训练营第42期 Day60打卡 - 图论Part10 - Bellman_ford算法系列运用
目录 一、Bellman_ford算法的应用 二、题目与题解 题目一:卡码网 94. 城市间货物运输 I 题目链接 题解:队列优化Bellman-Ford算法(SPFA) 题目二:卡码网 95. 城市间货物运输 II 题目链接 题解: 队列优…...

vue复制信息到粘贴框
npm install vue-clipboard2main.js文件引入 import VueClipboard from vue-clipboard2 Vue.use(VueClipboard)页面应用 copyInfo(info){let that thislet copyData 项目名称:${info.projectName}\n 用户名:${info.username}\n 初始密码:${…...
STM32基础笔记
第一章、STM32基本介绍 总内容 计算机技术简介环境安装、项目流程搭建最小系统时钟系统启动相关:启动文件、启动流程、启动方式GPIOUSARTNVIC: 外部中断_串口中断( DMA )TIMERADCDHT11: 单总线协议SPI : LCD屏 ## **1、计算机技术简介** 1.通用计算机/专用计算机…...

【深入学习Redis丨第六篇】Redis哨兵模式与操作详解
〇、前言 哨兵是一个分布式系统,你可以在一个架构中运行多个哨兵进程,这些进程使用流言协议来接收关于Master主服务器是否下线的信息,并使用投票协议来决定是否执行自动故障迁移,以及选择哪个Slave作为新的Master。 文章目录 〇、…...

开源项目 GAN 漫画风格化 UGATIT
开源项目:DataBall / UGATIT GitCode * 数据集 * [该项目制作的训练集的数据集下载地址(百度网盘 Password: gxl1 )](https://pan.baidu.com/s/1683TRcv3r3o7jSitq3VyYA) * 预训练模型 * [预训练模型下载地址(百度网盘 Password: khbg )](https://pan.ba…...

SegFormer网络结构的学习和重构
因为太多的博客并没有深入理解,本文是自己学习后加入自己深入理解的总结记录,方便自己以后查看。 segformer中encoder、decoder的详解。 学习前言 一起来学习Segformer的原理,如果有用的话,请记得点赞关注哦。 一、Segformer的网络结构图 网络结构&…...

ubuntu个人实用配置问题
记录两年前试图用Ubuntu作为自己的日常系统的实际情况 记录时间2022年8月26日 中间连输入法都安装不上。。哈哈又被自己笑到啦! ubuntu 安装 使用市面上的各种 U 盘启动盘制作工具,下载 iso 文件之后将清空指定的 U 盘并制作为启动 U 盘,…...

Xk8s证书续期
Master节点 备份文件 cp -r /etc/kubernetes/ /etc/kubernetes-20211021-bak tar -cvzf kubernetes-20211021-bak.tar.gz /etc/kubernetes-20211021-bak/cp -r ~/.kube/ ~/.kube-20211021-bak tar -cvzf kube-20211021-bak.tar.gz ~/.kube-20211021-bakcp -r /var/lib/kube…...

仓颉编程入门2,启动HTTP服务
上一篇配置了仓颉sdk编译和运行环境,读取一个配置文件,并把配置文件简单解析了一下。 前面读取配置文件,使用File.readFrom(),这个直接把文件全部读取出来,返回一个字节数组。然后又创建一个字节流,给文件…...

Linux驱动开发初识
Linux驱动开发初识 文章目录 Linux驱动开发初识一、驱动的概念1.1 什么是驱动:1.2 驱动的分类: 二、设备的概念2.1 主设备号&次设备号:2.2 设备号的作用: 三、设备驱动整体调用过程3.1 上层用户操控设备的流程:3.2…...
)
前端面试题(三)
11. Web API 面试题 如何使用 fetch 发起网络请求? fetch 是现代浏览器中用于发起网络请求的原生 API。它返回一个 Promise,默认情况下使用 GET 请求:fetch(https://api.example.com/data).then(response > response.json()).then(data &g…...

骨传导耳机哪个牌子最好用?实测五大实用型骨传导耳机分析!
在快节奏的现代生活中,耳机已成为我们不可或缺的伴侣。无论是在通勤路上、运动时,还是在安静的图书馆,耳机都能为我们提供一片属于自己的音乐天地。然而,长时间使用传统耳机可能会对听力造成损害,尤其是在高音量下。因…...
18.1 k8s服务组件之4大黄金指标讲解
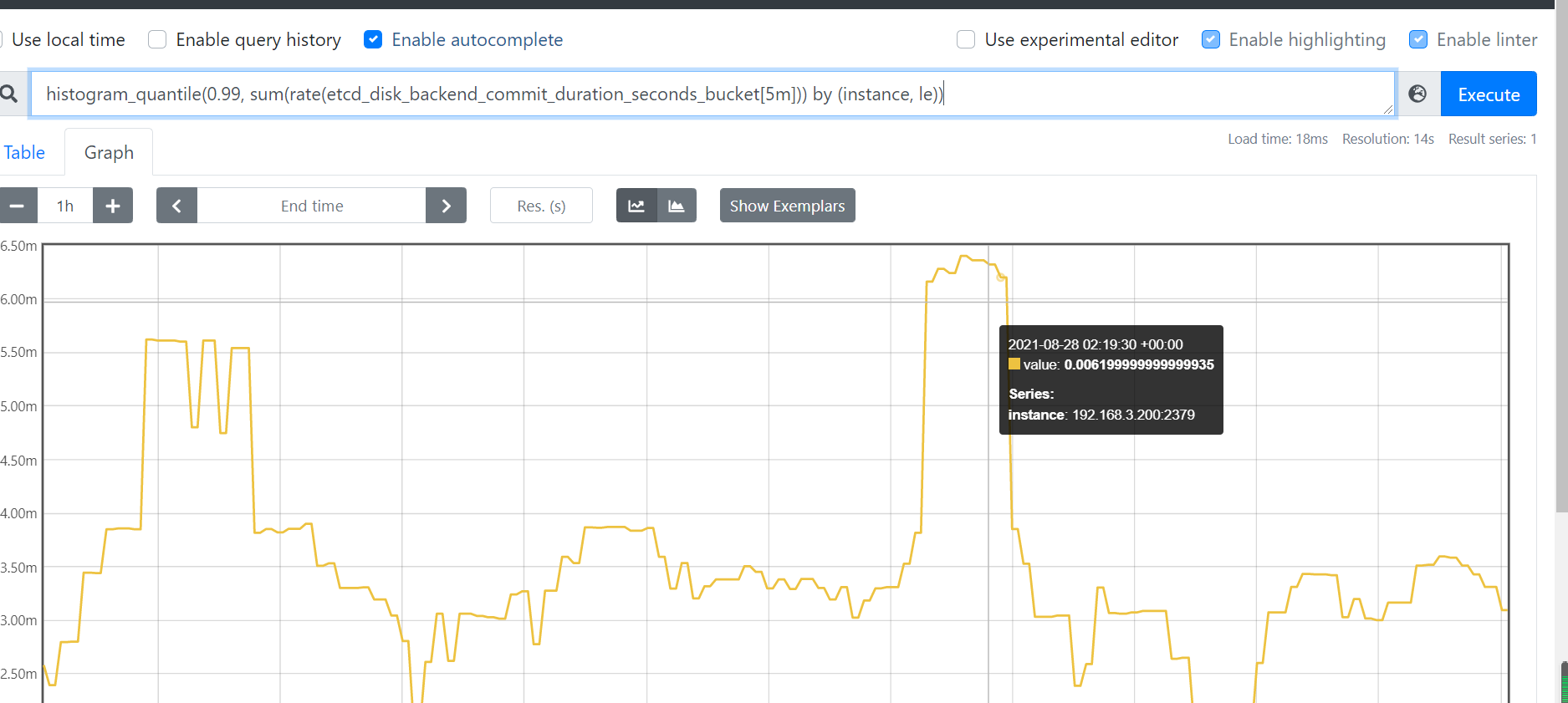
本节重点介绍 : 监控4大黄金指标 Latency:延时Utilization:使用率Saturation:饱和度Errors:错误数或错误率 apiserver指标 400、500错误qps访问延迟队列深度 etcd指标kube-scheduler和kube-controller-manager 监控4大黄金指标 …...

MacOS Catalina 从源码构建Qt6.2开发库之02: 配置QtCreator
安装Qt-creator-5.0.2 在option命令中配置Qt Versions指向 /usr/local/bin/qmake6 Kits选入CLang...

某建筑市场爬虫数据采集逆向分析
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言 目标网站 aHR0cHM6Ly9qenNjLm1vaHVyZC5nb3YuY24vZGF0YS9jb21wYW55P2NvbXBsZXhuYW1lPSVFNiVCMCVCNA 提示:以下是本篇文章正文内容,下面…...

降低存量房贷利率的主要原因和影响
降低存量房贷利率的主要原因和影响可以从以下几个方面来分析: 原因 刺激消费与内需:降低房贷利率可以减少贷款人的月供负担,增加家庭的可支配收入,理论上能刺激消费,促进经济的内循环。在经济面临压力时,这…...

远程桌面连接工具Microsoft Remote Desktop Beta for Mac
Microsoft Remote Desktop Beta for Mac 是一款功能强大的远程桌面连接工具,具有以下功能特点: 软件下载地址 跨平台连接: 允许 Mac 用户轻松连接到运行 Windows 操作系统的计算机,打破了操作系统的界限,无论这些 Wi…...

Linux 之 logrotate 【日志分割】
简介 logrotate 是一个用于管理日志文件的工具。它可以自动对日志文件进行轮转、压缩、删除等操作,以防止日志文件无限增长占用过多磁盘空间。logrotate 通常作为一个守护进程定期运行,也可以通过 cron 任务来调度执行 工作原理 按照配置文件中的规则…...

Canvas简历编辑器-Monorepo+Rspack工程实践
Canvas简历编辑器-MonorepoRspack工程实践 在之前我们围绕Canvas聊了很多代码设计层面的东西,在这里我们聊一下工程实践。在之前的文中我也提到过,因为是本着学习的态度以及对技术的好奇心来做的,所以除了一些工具类的库例如 ArcoDesign、Re…...

uni-app - - - - -vue3使用i18n配置国际化语言
uni-app - - - - -使用i18n配置国际化语言 1. 安装vue-i18n2. 配置文件2.1 创建如下文件2.2 文件配置2.3 main文件导入i18n 3. 页面内使用3.1 template内直接使用3.2 变量接收使用 1. 安装vue-i18n npm install vue-i18n --save2. 配置文件 2.1 创建如下文件 locales文件夹里…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...
