BFS 解决拓扑排序 , 课程表 , 课程表 II , 火星词典
文章目录
- 拓扑排序简介
- 1.有向无环图(DAG图)
- 2.AOV网:顶点活动图
- 3.拓扑排序
- 4.实现拓扑排序
- 207. 课程表
- 210. 课程表 II
- LCR 114. 火星词典
拓扑排序简介
1.有向无环图(DAG图)
像这样只能从一个点到另一个点有方向的图,并且不构成环状就是有向无环图

如果像这样,4,5,6就构成环状了,就不是有向无环图了。

出度是指一个顶点作为起点出发的边的数量,而入度是指指向该顶点的边的数量

2.AOV网:顶点活动图
在有向无环图中,用顶点来表示一个活动,用边来表示活动的先后顺序的图结构。
eg:

3.拓扑排序
找到做事情的先后顺序,拓扑排序的结果可能不是唯一的。
重要应用:判断有向图中是否有环
用上面那个炒菜的例子:
1.先把买菜拿出来(买菜没有被任何箭头指向,准备厨具也可以)

- 准备厨具和洗菜都可以拿出来

- 只能选择洗菜

5. 可以选择腌肉或者切菜(剩下依次类推)

如何排序
- 找出图中入度为0的点,然后输出
- 删除与该点连接的边
- 重复1,2操作,直到图中没有点或者没有入度为0的点(有可能有环)为止
4.实现拓扑排序
借助队列,来一次bfs即可
- 初始化,把所有入度为0的点加入队列中
- 当队列不为空的时候:
a. 拿出队头元素,加入最终结果中
b. 删除与该元素相连接的边;
c. 判断:与删除边相连接的点,是否入度变为0(如果入度为0,就加入队列)
207. 课程表

由题目可的建网类似这样:

实际上这道题就是在问:
能否拓扑排序
是否是有向无环图 - 有向图中是否有环?
如何建图 ? 灵活的使用容器
更倾向于unordered_map<int, vector> edgs; 建表,就像0 -> 1,2,3 ,好用。

class Solution {
public:bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {unordered_map<int,vector<int>> edges;//邻接表存图vector<int> in(numCourses); //标记每一个定义的入度//建图for(auto& e : prerequisites){int a = e[0], b =e[1]; //b -> aedges[b].push_back(a);in[a]++;}//拓扑排序 queue<int> q;//把所有入度为0的点的加入队列for(int i = 0; i<numCourses; i++){if(in[i] == 0)q.push(i);}//bfswhile(q.size()){int t = q.front();q.pop();for(auto a : edges[t]){in[a]--;if(in[a] == 0)q.push(a);}}//判断是否有环for(int i = 0; i<numCourses; i++){if(in[i])return false;}return true;}
};
210. 课程表 II

本质上跟上一道题一样,只不过这个让返回课程的学习顺序
我们只需要在每一次取出队列中最上面的时候,把它存入一个vector数组中即可,最后判断数组中的数和课程总数是否相等就可以。
class Solution {
public:vector<int> findOrder(int numCourses, vector<vector<int>>& prerequisites) {unordered_map<int,vector<int>> edgs;//邻接表存图vector<int> vis(numCourses);//标记每一个定义的入度//建表for(auto& e : prerequisites){int a = e[0],b = e[1]; //b->aedgs[b].push_back(a);vis[a]++;}//拓扑排序queue<int> q;vector<int> ret;//把所有入度为0的点放入队列for(int i = 0; i<numCourses; i++){if(vis[i] == 0)q.push(i);}while(q.size()){int t = q.front();ret.push_back(t);q.pop();for(auto a : edgs[t]){vis[a]--;if(vis[a] == 0)q.push(a);}}if(ret.size() == numCourses)return ret;else return {}; }
};
LCR 114. 火星词典

如何收集信息
用两层for循环来搜集信息

一遍一遍循环比较来建有向无环图

细节问题
像abc 和 ab 这种比较并不合法

class Solution {
public:unordered_map<char,unordered_set<char>> edges;//邻接表存图unordered_map<char,int> in; //统计入度bool valid; //处理边界情况string alienOrder(vector<string>& words) {int n = words.size();//建表+初始化入度哈希表for(auto& s : words){for(auto ch : s){in[ch] = 0;}}for(int i = 0; i<n; i++){for(int j = i+1; j<n; j++){add(words[i],words[j]);if(valid) return "";}}//拓扑排序queue<char> q;for(auto& [a,b] : in){if(b == 0) q.push(a); } string ret;while(q.size()){char t =q.front();q.pop();ret+=t;for(char ch : edges[t]){if(--in[ch] == 0)q.push(ch);}}//判断for(auto &[a,b] : in){if(b != 0)return "";}return ret;}void add(string& s1,string& s2){int n = min(s1.size(),s2.size());int i = 0;for(;i<n;i++){if(s1[i] != s2[i]){char a = s1[i];char b = s2[i];// a -> bif(!edges.count(a) || !edges[a].count(b)){edges[a].insert(b);in[b]++;}break;}}if(i == s2.size() && i < s1.size()) //判断不合法的情况valid = true;}
};
相关文章:

BFS 解决拓扑排序 , 课程表 , 课程表 II , 火星词典
文章目录 拓扑排序简介1.有向无环图(DAG图)2.AOV网:顶点活动图3.拓扑排序4.实现拓扑排序 207. 课程表210. 课程表 IILCR 114. 火星词典 拓扑排序简介 1.有向无环图(DAG图) 像这样只能从一个点到另一个点有方向的图&a…...

web安全攻防渗透测试实战指南_web安全攻防渗透测试实战指南,零基础入门到精通,收藏这一篇就够了
1. Nmap的基本 Nmap ip 6 ip Nmap -A 开启操作系统识别和版本识别功能 – T(0-6档) 设置扫描的速度 一般设置T4 过快容易被发现 -v 显示信息的级别,-vv显示更详细的信息 192.168.1.1/24 扫描C段 192.168.11 -254 上 nmap -A -T4 -v -i…...

大模型如何赋能智慧城市新发展?
国家数据局近期发布的《数字中国发展报告(2023)》显示,我国数据要素市场化改革步伐进一步加快,数字经济规模持续壮大,数字技术应用场景不断拓展。这一成就的背后是数字技术广泛应用,数字技术不仅影响着老百…...

随记——机器学习
前言 本来有个500块钱的单子,用机器学习做一个不知道什么鸟的识别,正好有数据集,跑个小项目,过一下机器学习图像识别的流程,用很短的时间记录下来..... 一、数据预处理 将数据集分为训练集和测试集,直接…...
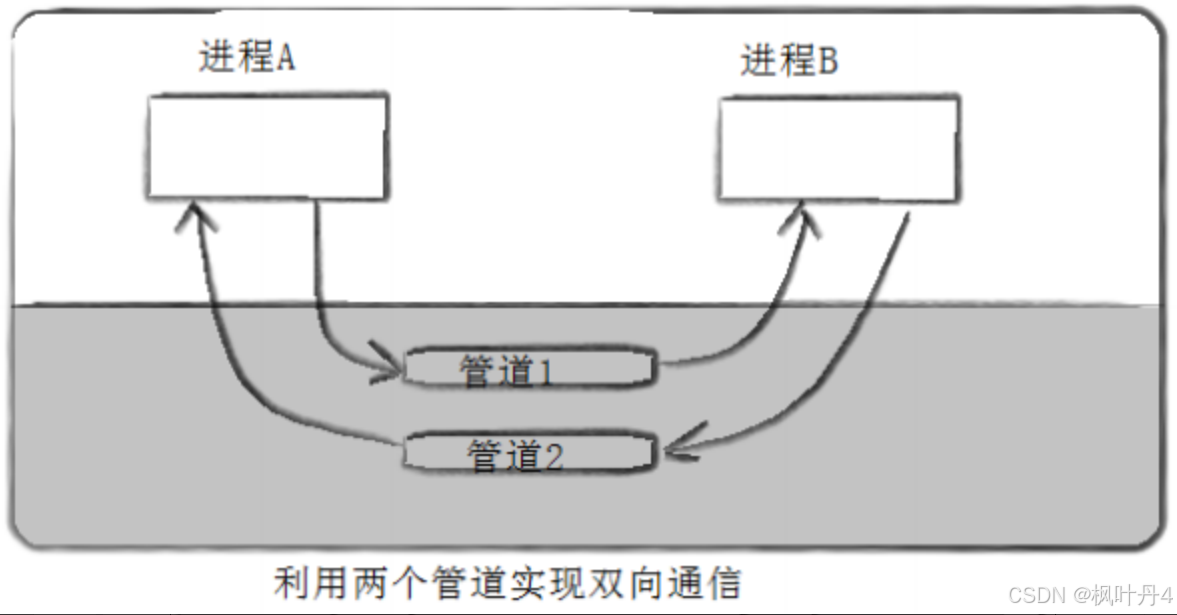
【在Linux世界中追寻伟大的One Piece】进程间通信
目录 1 -> 进程间通信介绍 1.1 -> 进程间通信目的 1.2 -> 进程间通信发展 1.3 -> 进程间通信分类 1.3.1 -> 管道 1.3.2 -> System V IPC 1.3.3 -> POSIX IPC 2 -> 管道 2.1 -> 什么是管道 2.2 -> 匿名管道 2.3 -> 实例代码 2.4 -…...
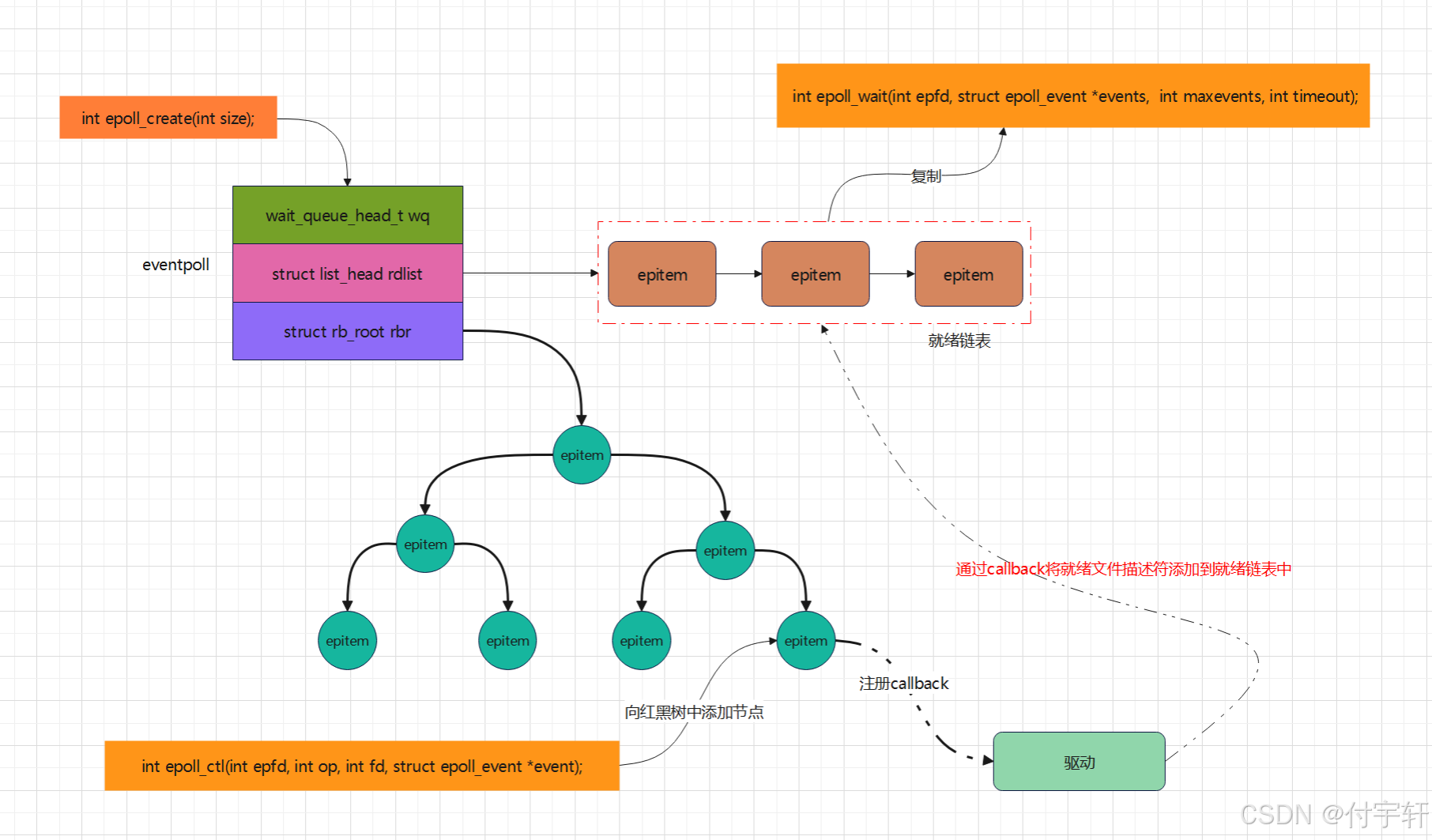
多路复用IO
一。进程处理多路IO请求 在没有多路复用IO之前,对于多路IO请求,一般只有阻塞与非阻塞IO两种方式 1.1 阻塞IO 需要结合多进程/多线程,每个进程/线程处理一路IO 缺点:客户端越多,需要创建的进程/线程越多,…...

C++ prime plus-7-編程練習
1, #include <iostream>// 函数声明 double harmonicMean(double x, double y);int main() {double x, y, result;while (true) {std::cout << "请输入两个数(其中一个为0时结束): ";std::cin >> x >> y;…...

计算1 / 1 - 1 / 2 + 1 / 3 - 1 / 4 + 1 / 5 …… + 1 / 99 - 1 / 100 的值,打印出结果
我们写这道题的时候需要俩变量接受,一个总数一个分母,我们发现分母变化是有规律的从1~100循环。 #include<stdio.h> int main() {int i 0;int tag 1;double sum 0.0;for (i 1; i < 101; i){if (i % 2 0){sum sum - 1.0 / i;}else{sum s…...
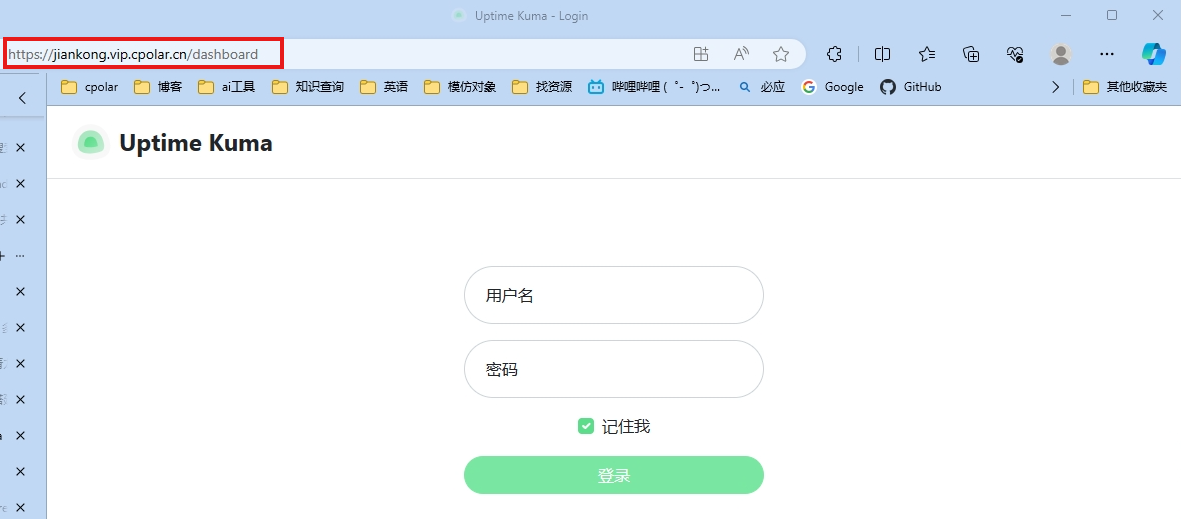
Linux本地服务器搭建开源监控服务Uptime Kuma与远程监控实战教程
文章目录 前言**主要功能**一、前期准备本教程环境为:Centos7,可以跑Docker的系统都可以使用本教程安装。本教程使用Docker部署服务,如何安装Docker详见: 二、Docker部署Uptime Kuma三、实现公网查看网站监控四、使用固定公网地址…...

JS 历史简介
目录 1. JS 历史简介 2. JS 技术特征 1. JS 历史简介 举例:在提交用户的注册信息的时候,为避免注册出现错误后重新填写信息,可以在写完一栏信息后进行校验,并提示是否出现错误,这样会大大提高用户提交的成功率&…...

爬虫逆向学习(七):补环境动态生成某数四代后缀MmEwMD
声明:本篇文章内容是整理并分享在学习网上各位大佬的优秀知识后的实战与踩坑记录 前言 这篇文章主要是研究如何动态生成后缀参数MmEwMD的,它是在文章爬虫逆向学习(六):补环境过某数四代的基础上进行研究的,代码也是在它基础上增…...

光伏电站并网验收需要注意什么细节
一、设备质量及安装验收 光伏组件:检查光伏组件的外观是否完好无损,无明显的缺陷和破损,表面是否清洁无污染。同时,需要验证光伏组件的型号、参数是否与设备台账资料一致。 逆变器:确认逆变器具备防雷、防尘、防潮等…...

页面禁用鼠标右键属于反爬虫措施吗 ?
是的,禁用鼠标右键通常被视为一种反爬虫(anti-scraping)措施。网站开发者常常采用这种技术来防止用户通过右键菜单复制文本、图像或其他内容,特别是在内容保护和数据安全方面。以下是禁用鼠标右键的一些背景和目的: 1…...
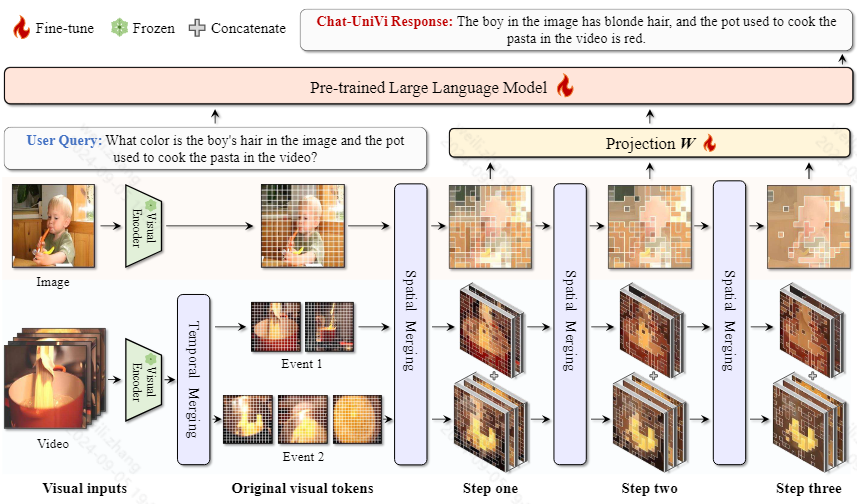
视频理解大模型最新进展
文章目录 Video-LLaMAVision-Language BranchAudio-Language Branch Video-ChatGPTMiniGPT4-videoCogVLM2-Video(1)Pre-training(2)Post-training Qwen2-VLMA-LMMChat-UniVi大模型对比 Video-LLaMA 2023:阿里达摩院的…...

cocos creator 使用 protobuf 的步骤与注意事项
移除可能曾安装过的protobuf // 移除全局 npm remove -g protobufjs npm remove -g protobufjs-cli npm remove -g pbjs // 移除项目中的 npm remove --save protobufjs npm remove --save protobufjs-cli npm remove --save pbjs全局安装 npm i -g protobufjs //或者 cnpm …...

mac访达查找文件目录
mac访达查找文件目录 在Mac上使用访达(Finder)查找文件或目录的方法如下: 打开访达。 在访达窗口的侧边栏中,选择“ Go to Folder”(转到文件夹)选项,或者使用快捷键ShiftCommandG打开一个对…...

【数据结构】点分治 点分树
求树上长度小于等于k的路径 #include <iostream> #include <cstring> #include <algorithm>using namespace std;const int N 10010, M N * 2;int n, m; int h[N], e[M], w[M], ne[M], idx; //邻接表 bool st[N]; //记录每个点是否被删掉 int p[N]; //存储…...

K8s Calico替换为Cilium,以及安装Cilium过程(鲁莽版)
迁移CNI插件的3种办法: 1、创建一个新的集群,通过Gitops的方式迁移负载,然而,这可能涉及大量的准备工作和潜在的中断。 2、另一种方法是重新配置/etc/cni/net.d/指向Cilium。但是,现有的pod仍将由旧的…...

背景图鼠标放上去切换图片过渡效果
文章目录 css鼠标放上去之前效果鼠标放上去时效果 css <li class"message"></li>.message {width: 22px;height: 22px;background-image: url(/assets/message-01.png);background-size: cover;background-position: center;transition: background-ima…...

【Linux】当前进展
驱动层日志添加了下文件目录,函数,代码行的打印(这里要小心,驱动目录源代码打印日志里边添进程号可能有问题,因为在驱动初始化的时候,内核还没有创建进程,不过猜测可以先不打印进程相关信息&…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...
中的KV缓存压缩与动态稀疏注意力机制设计)
大语言模型(LLM)中的KV缓存压缩与动态稀疏注意力机制设计
随着大语言模型(LLM)参数规模的增长,推理阶段的内存占用和计算复杂度成为核心挑战。传统注意力机制的计算复杂度随序列长度呈二次方增长,而KV缓存的内存消耗可能高达数十GB(例如Llama2-7B处理100K token时需50GB内存&a…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...
