蓝桥杯第19天(Python)(疯狂刷题第3天)
题型:
1.思维题/杂题:数学公式,分析题意,找规律
2.BFS/DFS:广搜(递归实现),深搜(deque实现)
3.简单数论:模,素数(只需要判断到 int(sqrt(n))+1),gcd,lcm,快速幂(位运算移位操作),大数分解(分解为质数的乘积)
4.简单图论:最短路(一对多(Dijstra,临接表,矩阵实现),多对多(Floyd,矩阵实现)),最小生成树(并查集实现)
5.简单字符串处理:最好转为列表操作
6.DP:线性DP,最长公共子序列,0/1背包问题,最长连续字符串,最大递增子串
7.基本算法:二分,贪心,组合,排列,前缀和,差分
8.基本数据结构:队列,集合,字典,字符串,列表,栈,树
9.常用模块:math,datetime,sys中的设置最大递归深度(sys.setrecursionlimit(3000000)),collections.deque(队列),itertools.combinations(list,n)(组合),itertools.permutations(list,n)(排列) heapq(小顶堆)
目录
题型:
刷题
1.阶乘约数 (大数分解,循环)
2.质因子个数 (大数分解,质数,约数)
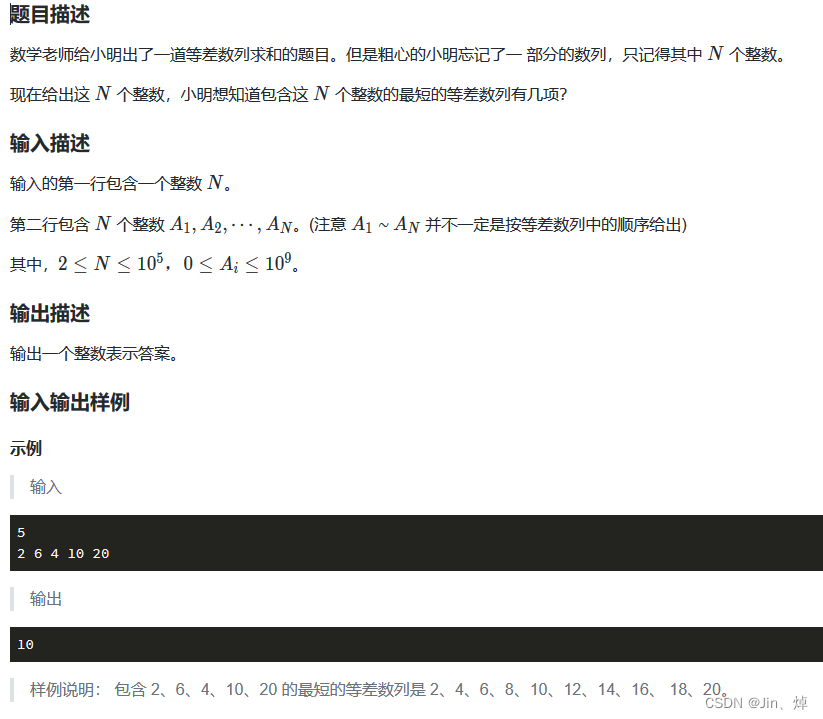
3.等差数列(gcd函数用法)
4.快速幂(Fast_pow,位运算,移位操作)
5.最大最小公倍数(贪心,枚举讨论)
6.分解质因数(大数分解,字符串处理函数)
7.裁纸刀(思维题,内置函数的使用)
8.蛇形填数(思维,观察规律)
9.最大降雨量(思维题)
10.排序(字典序)
11.聪明的猴子(最小生成树,并查集)
12.路径(floyd或者dijstra实现)
13.出差(最短路径,矩阵实现Dijstra算法)
14.蓝桥王国(Dijstra算法模板题)
15.蓝桥公园 (Floyd算法模板题)
刷题
1.阶乘约数 (大数分解,循环)

import sys #设置递归深度
import collections #队列
import itertools # 排列组合
import heapq #小顶堆
import math
sys.setrecursionlimit(300000)#写法一
save=[0]*101 # 大数分解
for i in range(1,101):for j in range(2,int(math.sqrt(i))+1): # 质数从2开始while i%j==0: # 质数分解save[j]+=1i=i//jif i>1: # 剩下的数是一个质数或者本身就是一个质数 例如10=2*5 17=1*17save[i]+=1ans=1
for i in save:ans*=(i+1)
print(ans)# 写法二
##MAXN = 110
##cnt = [0] * MAXN #记录对应质数幂次
##
##for i in range(1, 101):
## x = i
## # 质因子分解
## j = 2
## while j * j <= x:
## if x % j == 0: # 是一个质数约数
## while x % j == 0: #类似埃式筛
## x //= j
## cnt[j] += 1
## j += 1
## if x > 1:
## cnt[x] += 1
##
##ans = 1
##for i in range(1, 101):
## if cnt[i] != 0:
## ans *= (cnt[i] + 1) # 0 也是一种选择
##
##print(ans)两种实现方法,因为是100!,所以需要遍历1-100进行大数分解,注意质数是从2开始的,1不是质数,只需要遍历2 - int( sqrt(n) )区间是否有n的因子,python取不到后面一位所以要加1,没得说明他是质数,同时如果分解后大于1说明没有被分解完,剩下的为质数,例如10,不是质数会变为1,例如4,9
2.质因子个数 (大数分解,质数,约数)

import sys #设置递归深度
import collections #队列
import itertools # 排列组合
import heapq #小顶堆
import math
sys.setrecursionlimit(300000)#对一个数进行大数分解
ans=0
n=int(input())
for i in range(2,int(math.sqrt(n))+1):if n%i==0: #发现质数ans+=1#print(i) # 打印质数约数while n%i==0: # 消除这个质数n=n//i
if n>1:#print(n) # 打印质数约数ans+=1
print(ans)
送分题,会了第一题这道题就是秒出答案,只需要分解这一个数就行了,只需要求有多少个质数,注意判断分解后如果剩下的数大于1,说明还剩下了一个质数,答案需要加1.
3.等差数列(gcd函数用法)
import sys #设置递归深度
import collections #队列
import itertools # 排列组合
import heapq #小顶堆
import math
sys.setrecursionlimit(300000)# gcd(0,a)=an=int(input())
A=list(map(int,input().split()))
d=0
for i in range(len(A)-1):d=math.gcd(d,A[i+1]-A[i])#print(d) #打印d# 需要处理d==0的情况
if d==0:print(n)
else:ans=(max(A)-min(A))//d+1print(ans)送分题,但是需要仔细判断情况,之前一直漏掉了d==0时的情况,没有考虑周全,出现÷0错误,需要注意gcd(0,a)= a,当不确定长度,边界范围的时候自己举例来确定。
4.快速幂(Fast_pow,位运算,移位操作)

import sys #设置递归深度
import collections #队列
import itertools # 排列组合
import heapq #小顶堆
import math
sys.setrecursionlimit(300000)b,p,q = map(int,input().split())
ans=1
while p: # 8次方 转为二进制 1000if p&1: #当前位有1ans=ans%q * bb=b*b%qp=p>>1 # 右移即/2
print(ans%q)算是送分题,需要掌握位运算,左移乘2右移除2,使用while语句循环的时候注意在最后要改值,例如左加右减,右移左移,防止死循环。
5.最大最小公倍数(贪心,枚举讨论)

import sys #设置递归深度
import collections #队列
import itertools # 排列组合
import heapq #小顶堆
import math
sys.setrecursionlimit(300000)n=int(input())
# 第一时间想到 n*(n-1)*(n-2)
# 当n为奇数 最大值 n*(n-1)*(n-2)
# 当n为偶数 n和n-2可以约分
# n*(n-1)*(n-3) (不能被3整除)
# (n-1)*(n-2)*(n-3) (能被3整除)if n%2==1:print(n*(n-1)*(n-2))
else:if n%3==0: #能被3整除print((n-1)*(n-2)*(n-3))else:print(n*(n-1)*(n-3))枚举所有情况,首先按照贪心想法取3个最大值,然后在讨论特殊情况,例如有约数这些,要找互质的。因为求最小公倍数最大值。
6.分解质因数(大数分解,字符串处理函数)
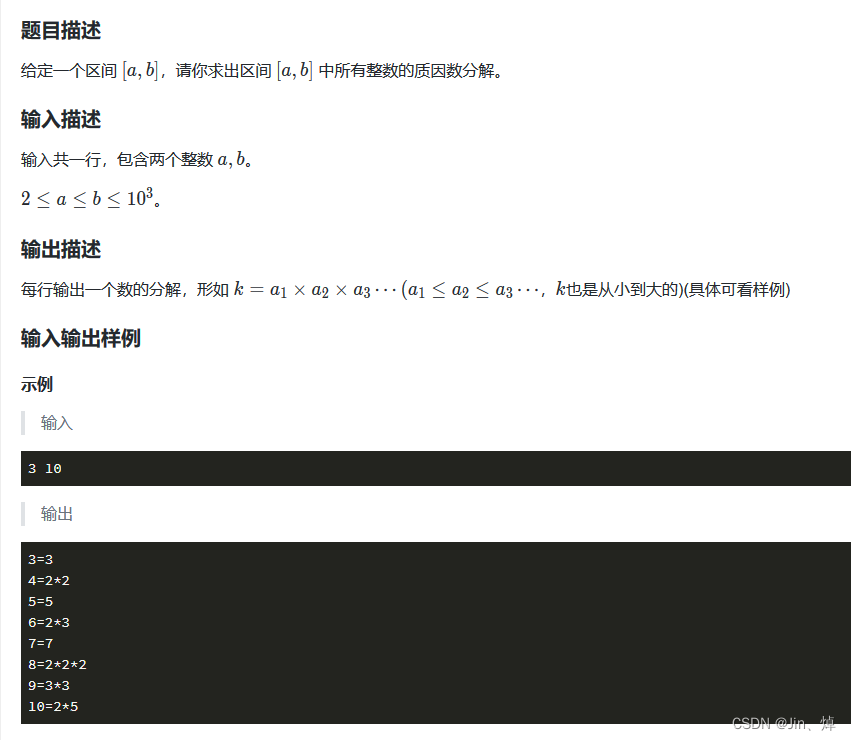
import sys #设置递归深度
import collections #队列
import itertools # 排列组合
import heapq #小顶堆
import math
sys.setrecursionlimit(300000)a,b=map(int,input().split())
for i in range(a,b+1):save=ians=[] # 保存分解的数for j in range(2,int(math.sqrt(i))+1):if i%j==0:while i%j==0:ans.append(str(j))i=i//jif i >1: # 剩下的质数或者本身是质数没有分解,例如15,5,7ans.append(str(i))print(str(save)+'='+'*'.join(ans)) # " ".join(list) list里面的元素需要为字符类型遍历这些数,对每一个数进行大数分解,难点在于知道分解后如果n值>1,说明分解后剩下了一个质数或者本身是质数不能分解为其他质数,然后就是字符串拼接操作,join()函数需要连接元素为字符串的才可以。
7.裁纸刀(思维题,内置函数的使用)

没什么难点,属于送分,需要读懂题意,就只有两种分法,使用内置函数min()取最小值就可以了,送分!!
8.蛇形填数(思维,观察规律)

求的是对角线上元素,观察对角线上元素的规律,即 +4 +8 +12 ,发现规律了直接套一个循环就可以了。
9.最大降雨量(思维题)


34 ---------> 49-15=34,上面手误了
思维题,注意重点,即两个中位数,不确定的时候举例,举特例来证明结论。
10.排序(字典序)

理解字典序的含义,即 'a'>'b',' a' > 'ab','ab'>'b'。这道题要求最短同时按照字典序,所以固定了答案,同时需要了解全排列,即 N*(N-1)/2 ,即 bca 排列成abc全排列 3*2/2=3
11.聪明的猴子(最小生成树,并查集)

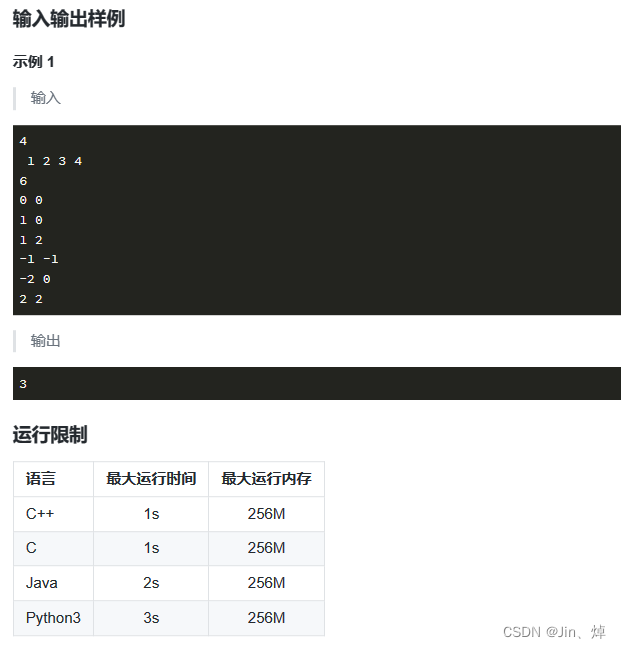
import sys #设置递归深度
import collections #队列
import itertools # 排列组合
import heapq #小顶堆
import math
sys.setrecursionlimit(300000)def find(x):if x==f[x]:return f[x]else:f[x]=find(f[x])return f[x]def merge(x,y):if find(x)!=find(y): # 需要合根,默认合向yf[find(x)]=find(y) # x的根指向y的根m=int(input()) # 猴子树
leng=list(map(int,input().split())) # 存储跳跃距离n=int(input()) # 边数
dis = [0] # 存储坐标
for i in range(n): dis.append(list(map(int,input().split())))edge=[] #存储边
for i in range(1,n+1):for j in range(i+1,n+1):w=math.sqrt((dis[i][0]-dis[j][0])**2+(dis[i][1]-dis[j][1])**2) #计算距离edge.append((i,j,w)) # 添加边,总共添加n*(n-1)/2条边
edge.sort(key=lambda x:x[2]) # 边从小到大排序Max=0
num=0 # 当前处理了多少条边
f=[ i for i in range(n+1)]
for i in edge:if find(i[0]) !=find(i[1]): # 最小生成树算法处理merge(i[0],i[1])Max=max(Max,i[2]) #在遍历过程中记录下最长边num+=1if num==(n-1): # 已经构建好了最小生成树breakans=0 # 记录能跳的猴子数量
for i in leng:if i>=Max:ans+=1print(ans)熟悉并查集的使用,最小生成树的构建方法,学会通过并查集,使用Kruskal Algorithm算法,即边从大到小排序,依次遍历最短边来构建最小生成树的方法来构建最小生成树。
12.路径(floyd或者dijstra实现)

import sys #设置递归深度
import collections #队列
import itertools # 排列组合
import heapq #小顶堆
import math
sys.setrecursionlimit(300000)# 初始化边
dp=[[2**100]*2030 for i in range(2030)]def lcm(a,b):return a//math.gcd(a,b)*b
# 赋初值
for i in range(1,2022):for j in range(i+1,i+22): # 取不到最后一位if j>2021:breakdp[i][j]=lcm(i,j)# floyd 算距离
for k in range(1,2022):for i in range(1,2):for j in range(1,2022):dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j])print(dp[1][2021])floyd算法求得是多对多,但是时间复杂度为3阶多项式复杂度,Dijstra复杂度低一些,求的是1到多,floyd算法可以转换为求1到多,多到多,多到1。本题难点在于floyd算法的掌握,同时需要注意,floyd是通过矩阵实现的。
import sys #设置递归深度
import collections #队列
import itertools # 排列组合
import heapq #小顶堆
import math
sys.setrecursionlimit(300000)# Dijstr实现
def lcm(a,b):return a//math.gcd(a,b)*b
def dij(s):done=[0]*2022 # 标记是否处理过hp=[]dis[s]=0 # 自身到自身的距离为0heapq.heappush(hp,(0,s)) # 入堆while heapq:u=heapq.heappop(hp)[1] # 出堆元素结点,边最小if done[u]==0: # 没有被处理过done[u]=1#for i in dp[u]: # 遍历u的邻居 i:(v,w)for i in range(len(dp[u])): # 遍历u的邻居 i:(v,w)v,w=dp[u][i]if done[v]==0: # 没有被处理过dis[v]=min(dis[v],dis[u]+w)heapq.heappush(hp,(dis[v],v))dp=[[] for i in range(2022)] # 邻接表
dis=[2**100] * 2022 # 初始
# 邻接表更新
for i in range(1,2022):for j in range(i+1,i+22):if j>2021:breakdp[i].append((j,lcm(i,j))) # 邻居和边长s=1 # 开始起点
dij(s)
print(dis[2021])13.出差(最短路径,矩阵实现Dijstra算法)


import sys #设置递归深度
import collections #队列
import itertools # 排列组合
import heapq #小顶堆
import math
sys.setrecursionlimit(300000)def dij():dist[1]=0 #很重要for _ in range(n-1): # 还有n-1个点没有遍历t=-1for j in range(1,n+1):if st[j]==0 and (t==-1 or dist[t]>dist[j]): #找到没处理过得最小距离点t=jfor j in range(1,n+1):dist[j]=min(dist[j],dist[t]+gra[t][j]) # t-j的距离,找最小值st[t]=1 # 标记处理过return dist[n]n,m=map(int,input().split())#下标全部转为从1开始
stay=[0]+list(map(int,input().split()))
stay[n]=0
gra = [[float('inf')] * (n+1) for _ in range(n+1)]
dist = [float('inf')] * (n+1)
st=[0]*(n+1) # 标志是否处理for i in range(m):u,v,w=map(int,input().split()) #这里重构图gra[u][v]=stay[v]+wgra[v][u]=stay[u]+wprint(dij())本题难点在于重新搭建图,即将在每个城市滞留的时间更新到图里面。同时,DIjstra算法也很重要。
模板:(邻接表)
通过heapq实现,临接表存储(v,w),使用小顶堆存储,每次出堆得到初始距离最小距离的顶点,然后判断他的临接点是否被处理过,没有就更新这些临接点的距离,然后将计算后的距离入堆,要有标记矩阵,距离矩阵,邻接表
模板:(矩阵)
通过矩阵实现存储边信息,进行n-1次循环处理剩下的点,寻找没处理过得距离初始点最短的点,然后通过他更新其他点离初始点距离值,找到最小值。需要标记矩阵,距离矩阵,,矩阵存储边。
Bellman-ford算法
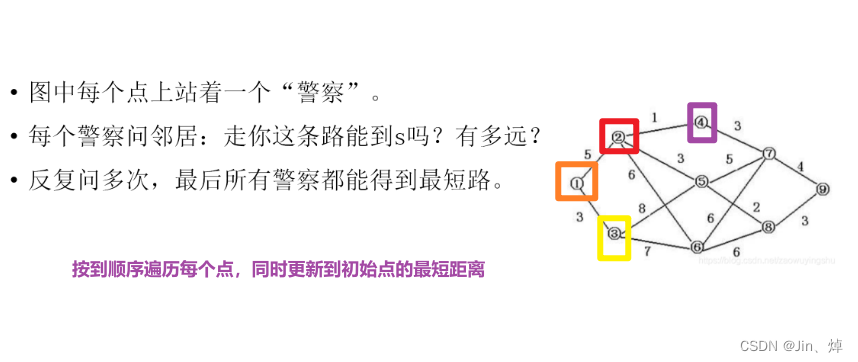


n,m=map(int,input().split())
t=[0]+list(map(int,input().split()))
e=[] #简单的数组存边for i in range(1,m+1):a,b,c = map(int,input().split())e.append([a,b,c]) # 双向边e.append([b,a,c])dist=[2**50]*(n+1)
dist[1]=0for k in range(1,n+1): # 遍历每个点,n个点,执行n轮问路for a,b,c in e: # 检查每条边,每一轮问路,检查所有边res=t[b]if b==n:res=0dist[b]=min(dist[b],dist[a]+c+res) # 更新路径长度print(dist[n])
14.蓝桥王国(Dijstra算法模板题)


import heapq # 导入堆
def dij(s):done=[0 for i in range(n+1)] # 记录是否处理过hp=[] #堆dis[s]=0heapq.heappush(hp,(0,s)) #入堆,小顶堆while hp:u=heapq.heappop(hp)[1] #出堆元素结点if done[u]: #当前结点处理过continuedone[u]=1for i in range(len(G[u])): #遍历当前结点的邻居v,w =G[u][i]if done[v]:continuedis[v]=min(dis[v],dis[u]+w) # 更新当前结点邻居的最短路径heapq.heappush(hp,(dis[v],v))n,m = map(int,input().split())#
s=1 # 从1开始访问
G=[[]for i in range(n+1)] #邻接表存储
inf = 2**50
dis = [inf]*(n+1) #存储距离
for i in range(m):# 存边,这里是单向边u,v,w = map(int,input().split())G[u].append((v,w)) #记录结点u的邻居和边长dij(s)
for i in range(1,n+1):if dis[i]==inf:print("-1",end=' ')else:print(dis[i],end=' ')模板题,需要熟练掌握和牢记,这是通过heapq小顶堆实现的,掌握模板就可以了
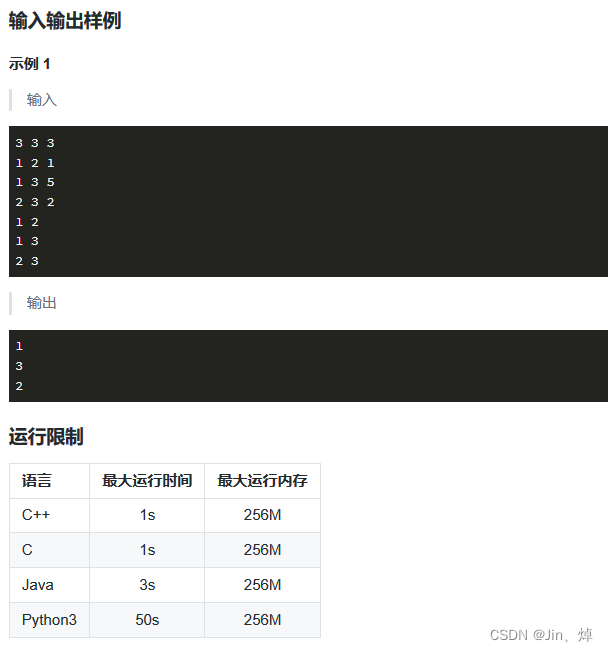
15.蓝桥公园 (Floyd算法模板题)

import os
import sys# 请在此输入您的代码
#floyd算法,多对多def floyd():global dpfor i in range(1,n+1):for j in range(1,n+1):for k in range(1,n+1):dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j])n,m,q = map(int,input().split())
inf=2**120
dp=[[inf]*(n+1) for i in range(n+1)]
choice=[]
for i in range(m):u,v,w=map(int,input().split())dp[u][v]=wdp[v][u]=w
for i in range(q):s,d = map(int,input().split())choice.append((s,d))
floyd()
for s,d in choice:if dp[s][d]!=inf:print(dp[s][d])continueprint(-1)Floyd算法模板题,熟练掌握就可以了,floyd用于多对多!
相关文章:

蓝桥杯第19天(Python)(疯狂刷题第3天)
题型: 1.思维题/杂题:数学公式,分析题意,找规律 2.BFS/DFS:广搜(递归实现),深搜(deque实现) 3.简单数论:模,素数(只需要…...
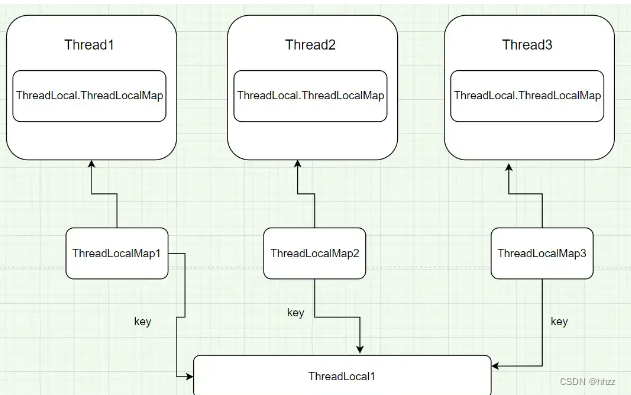
【数据库连接,线程,ThreadLocal三者之间的关系】
一、数据库连接与线程的关系 在实际项目中,数据库连接是很宝贵的资源,以MySQL为例,一台MySQL服务器最大连接数默认是100, 最大可以达到16384。但现实中最多是到200,再多MySQL服务器就承受不住了。因为mysql连接用的是tcp协议&…...
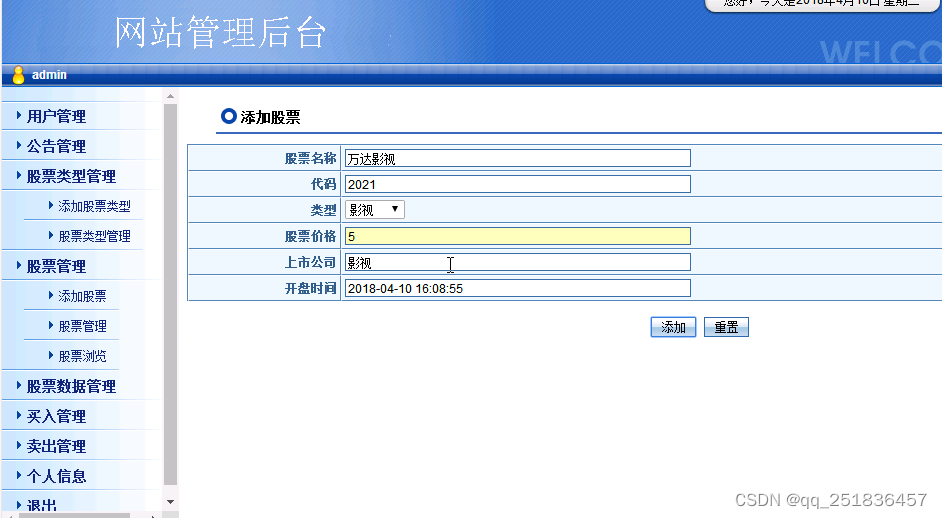
java 虚拟股票交易系统Myeclipse开发mysql数据库web结构jsp编程计算机网页项目
一、源码特点 JSP 虚拟股票交易系统是一套完善的java web信息管理系统,对理解JSP java编程开发语言有帮助,系统采用serlvetdaobean,系统具有完整的源代码和数据库,系统主要采用 B/S模式开发。 java 虚拟股票交易系统Myeclips…...

spring如何开启允许循环依赖
如何解决spring循环依赖 在Spring框架中,allowCircularReferences属性是用于控制Bean之间的循环依赖的。循环依赖是指两个或多个Bean之间相互依赖的情况,其中一个Bean依赖于另一个Bean,同时另一个Bean又依赖于第一个Bean。 allowCircularRe…...
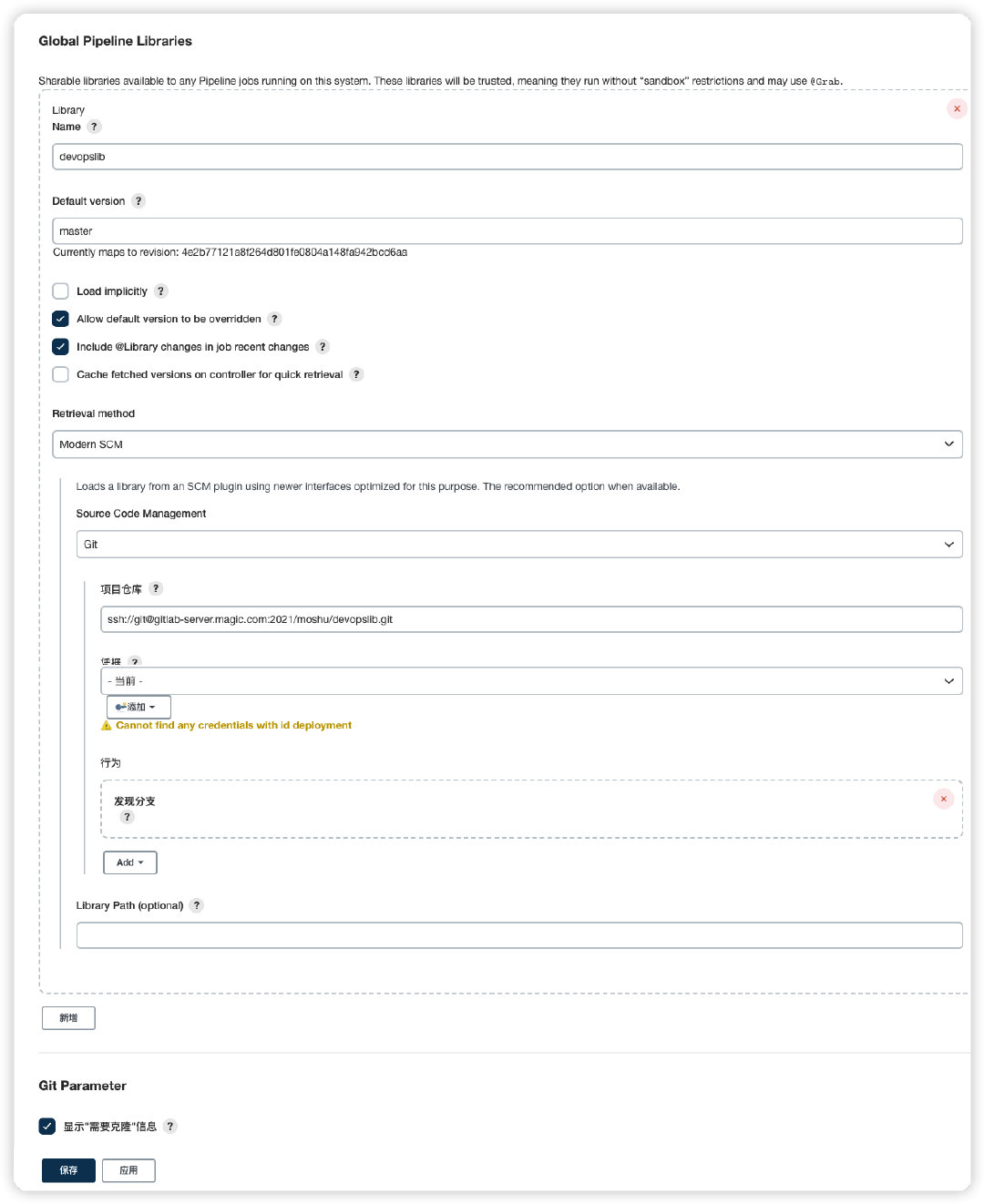
jenkins+sonarqube+自动部署服务
一、jenkins 配置Pipeline 二、新建共享库执行脚本 共享库可以是一个普通的gitlab项目,目录结构如下 三、添加到共享库 Jenkins Dashboard–>系统管理–>系统配置–>Global Pipeline Libraries Name: 共享库名称,自定义即可; Defa…...

【算法系列之动态规划III】背包问题
背包问题 01背包指的是物品只有1个,可以选也可以不选。完全背包是物品有无数个,可以选几个也可以不选。 二维数组01背包 有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次&…...

MONAI-LayerFactory设计与实现
LayerFactory 用于创建图层的工厂对象,这使用给定的工厂函数来实际产生类型或构建可调用程序。这些函数是通过名称来参考的,可以在任何时候添加。 用到的关键技术点: 装饰器(Decorators), 例如:property装饰器,创建…...

Thinkphp 6.0路由的定义
本节课我们来了解一下路由方面的知识,然后简单的使用一下路由的功能。 一.路由简介 1. 路由的作用就是让 URL 地址更加的规范和优雅,或者说更加简洁; 2. 设置路由对 URL 的检测、验证等一系列操作提供了极大的便利性; …...

Kafka系列之:深入理解Kafka集群调优
Kafka系列之:深入理解Kafka集群调优 一、Kafka硬件配置选择二、Kafka内存选择三、CPU选择四、网络选择五、生产者调优六、broker调优七、消费者调优八、Kafka总体调优一、Kafka硬件配置选择 服务器台数选择: 2 * (生产者峰值生产速率 * 副本数 / 100) + 1磁盘选择: Kafka…...

creator-泄漏检测之资源篇
title: creator-泄漏检测之资源篇 categories: Cocos2dx tags: [creator, 优化, 泄漏, 内存] date: 2023-03-29 14:48:48 comments: false mathjax: true toc: true creator-泄漏检测之资源篇 前篇 资源释放 - https://docs.cocos.com/creator/manual/zh/asset/release-manager…...
)
【DevOps】Jenkins 运行任务时遇到 FATAL:Unable to produce a script file 报错(已解决)
文章目录一、问题描述二、定位原因三、解决方案四、其他方案五、总结关键词: Jenkins、Unable to produce a script file、UnmappableCharacterException、IOException: Failed to create a temp file on一、问题描述 由于使用的 Jenkins 存在安全漏洞(…...

Web前端
WEB前端 HTMLCSSJavaScriptjQuery(js框架)Bootstrap(CSS框架)AJAXJSON 文章目录 WEB前端WEB前端三大核心技术Web开发工具文本编辑器集成开发环境(IDE)浏览器选择HTML什么是 HTML?HTML版本变迁HTML-HelloWorldHTML 文档 = 网页HTML 标签属性(Attribute)HTML 常用标签...
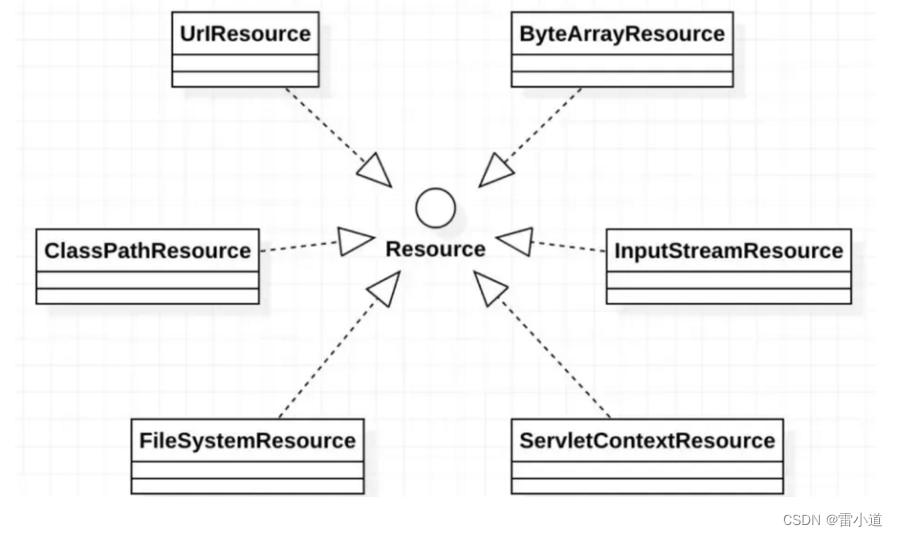
资源操作:Resources
文章目录1. Spring Resources概述1.2 Resource 接口1.3 Resource的实现类1.3.1 UrlResource访问网络资源1.3.2 ClassPathResource访问类路径下资源1.3.3 FileSystemResource访问文件系统资源1.3.4 ServletContextResource1.3.5、InputStreamResource1.3.6、ByteArrayResource1.…...
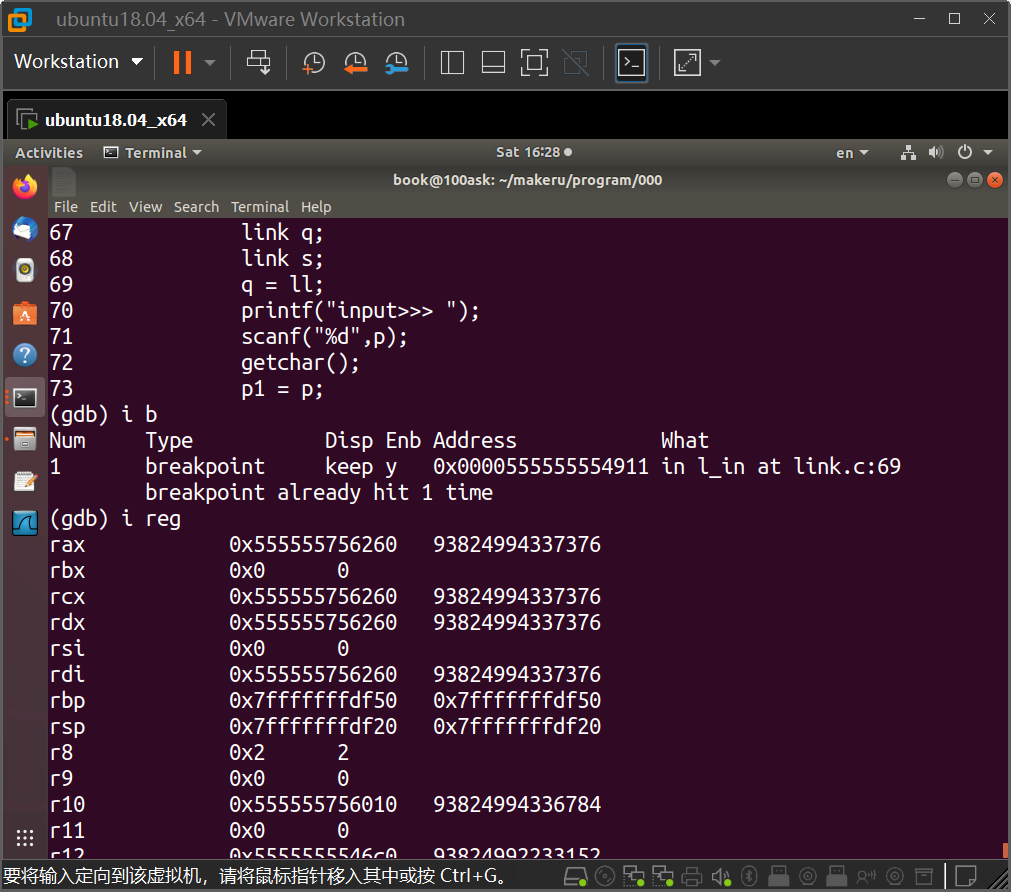
GDB调试的学习
很早就想在好好学一学gdb了,正好最近学算法(以前一直以为干硬件不需要什么特别厉害的算法,结果现在卷起来了。大厂面试题也有复杂一些的算法了) 下面的这些命令是别的博主总结的 GDB 调试过程_gdb调试过程_麷飞花的博客-CSDN博客…...
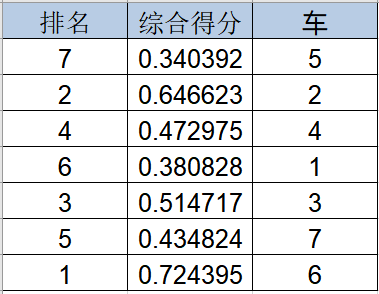
熵值法综合评价分析流程
熵值法综合评价分析流程 一、案例背景 当前有一份数据,是各品牌车各个维度的得分情况,现在想要使用熵值法进行综合评价,得到各品牌车的综合得分,从而进行车型优劣对比,为消费者提供购车依据。 数据如下(数…...

使用Python Pandas库操作Excel表格的技巧
在数据分析和处理中,我们经常需要对Excel表格进行操作。Python Pandas库提供了丰富的API来读取、写入、修改Excel表格。本文将介绍如何使用Python Pandas库操作Excel表格,包括向Excel表格添加新行、创建Excel表格等。 1.向Excel表格添加新行 下面是一个…...
LeetCode练习七:动态规划上:线性动态规划
文章目录一、 动态规划基础知识1.1 动态规划简介1.2 动态规划的特征1.2.1 最优子结构性质1.2.2 重叠子问题性质1.2.3 无后效性1.3 动态规划的基本思路1.4 动态规划基础应用1.4.1 斐波那契数1.4.2 爬楼梯1.4.3 不同路径1.5 个人总结二、记忆化搜索2.1 记忆化搜索简介2.2 记忆化搜…...

基于正点原子F407开发版和SPI接口屏移植touchgfx完整教程(一)
一、相关软件包安装 1、打开cubemx包管理器 2、安装F4软件包 3、安装touchgfx软件包 二、工程配置 1、新建工程 2、sys配置 3、rcc配置 4、crc配置 5、添加touchgfx软件包 6、配置touchgfx软件包 将width和height改为自己屏幕尺寸 7、生成工程 三、代码修改 1、将屏幕相关驱…...

Linux--进程间通信
前言 上一篇相关Linux文章已经时隔2月,Linux的学习也相对于来说是更加苦涩;无妨,漫漫其修远兮,吾将上下而求索。 下面该片文章主要是对进程间通信进行介绍,还对管道,消息队列,共享内存,信号量都…...

hadoop伪分布式集群搭建
基于hadoop 3.1.4 一、准备好需要的文件 1、hadoop-3.1.4编译完成的包 链接: https://pan.baidu.com/s/1tKLDTRcwSnAptjhKZiwAKg 提取码: ekvc 2、需要jdk环境 链接: https://pan.baidu.com/s/18JtAWbVcamd2J_oIeSVzKw 提取码: bmny 3、vmware安装包 链接: https://pan.baidu…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

Map相关知识
数据结构 二叉树 二叉树,顾名思义,每个节点最多有两个“叉”,也就是两个子节点,分别是左子 节点和右子节点。不过,二叉树并不要求每个节点都有两个子节点,有的节点只 有左子节点,有的节点只有…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

Redis上篇--知识点总结
Redis上篇–解析 本文大部分知识整理自网上,在正文结束后都会附上参考地址。如果想要深入或者详细学习可以通过文末链接跳转学习。 1. 基本介绍 Redis 是一个开源的、高性能的 内存键值数据库,Redis 的键值对中的 key 就是字符串对象,而 val…...

