【算法系列之动态规划III】背包问题
背包问题
- 01背包指的是物品只有1个,可以选也可以不选。
- 完全背包是物品有无数个,可以选几个也可以不选。
二维数组01背包
有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
输入:
weight: [1,3,4],value: [15,20,30],背包体积: 4
输出:35
解题思路
- dp数组,从下标[0-i]的物品里面任意取,放进容量为j的背包,价值总和最大是多少。
- 不放物品i,物品i由于体积问题放不进去,
dp[i][j]=dp[i-1][j] - 放物品i,
dp[i][j]=dp[i-1][j-weight[i]]+value[i]
Java实现
public class BagProblem {public static void main(String[] args) {int[] weight = {1, 3, 4};int[] value = {15, 20, 30};int bagSize = 4;System.out.println(new BagProblem().testWeightBagProblem(weight, value, bagSize));}public int testWeightBagProblem(int[] weight, int[] value, int bagSize) {int size = weight.length;//0-size-1个物品放入到大小为bagSize的背包中int[][] dp = new int[size][bagSize + 1];//当bagSize=0时,dp[i][0]=0//当只有索引为0的物品可以选择,且放的下(j<=bagSize),dp[0][j]的值等于放入索引为0的价值for (int j = weight[0]; j <= bagSize; j++) {dp[0][j] = value[0];}for (int i = 1; i < size; i++) {for (int j = 1; j <= bagSize; j++) {if (j < weight[i]) {/*** 当前背包的容量都没有当前物品i大的时候,是不放物品i的* 那么前i-1个物品能放下的最大价值就是当前情况的最大价值*/dp[i][j] = dp[i - 1][j];} else {dp[i][j] = Math.max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);}}}for (int i = 0; i < size; i++) {for (int j = 0; j <= bagSize; j++) {System.out.print(dp[i][j] + "\t");}System.out.println("\n");}return dp[size - 1][bagSize];}
}
一维数组01背包
解题思路
- dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j]。
- 递推公式:
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]); - 遍历详解:当i=0,初始化dp[j],只有j>weight[i]的时候,会被初始化。当i=1的时候,可以选择的商品有[0,1],dp[j]是在原有的dp数组上判断的,只有当可以存放下索引为1的商品,且
dp[j - weight[i]] + value[i]>dp[j],该数值才会被更新。 - 选择逆序背包容量,主要是dp[j]和dp[j-weight[i]]的初始化顺序的问题。在二维数组中,比较的是
dp[i-1][j-weight[i]],是第i-1层的dp[j-weight[i]]
Java实现
public class BagProblem_II {public static void main(String[] args) {int[] weight = {1, 3, 4};int[] value = {15, 20, 30};int bagWight = 4;System.out.println(new BagProblem_II().testWeightBagProblem(weight, value, bagWight));}private int testWeightBagProblem(int[] weight, int[] value, int bagWeight) {int wLen = weight.length;//定义dp数组:dp[j]表示背包容量为j时,能获得的最大价值int[] dp = new int[bagWeight + 1];//遍历顺序:先遍历物品,再遍历背包容量for (int i = 0; i < wLen; i++) {for (int j = bagWeight; j >= weight[i]; j--) {dp[j] = Math.max(dp[j], dp[j - weight[i]] + value[i]);System.out.println(dp[j] + "," + j + "," + i);}}//打印dp数组for (int j = 0; j <= bagWeight; j++) {System.out.print(dp[j] + " ");}System.out.println();return dp[bagWeight];}
}
416. 分割等和子集
力扣题目链接
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
输入:nums = [1,5,11,5]
输出:true
解释:数组可以分割成 [1, 5, 5] 和 [11] 。
解题思路
- 集合里能否出现总和为 sum / 2 的子集
- dp[j]:最大值为j的子集
- 如果第i个元素没有放到集合中,值是
dp[i-1][j];如果第i个元素放进集合中,值是dp[i-1][j-num[i]]+num[i]。
dp[i][j]= dp[i−1][j],当i-1的数组已经满足了等于j的条件
dp[i][j]= true, 当nums[i] = j满足。
dp[i−1][j−nums[i]].当nums[i] < j。
dp[i][j]为true的三个条件,只需要满足一个即可。
Java实现
public boolean canPartition(int[] nums) {if (nums == null || nums.length == 0) return false;int len = nums.length;int sum = 0;for (int i = 0; i < nums.length; i++) {sum += nums[i];}if (sum % 2 != 0) {return false;}int target = sum / 2;int[] dp = new int[target + 1];for (int i = 0; i < len; i++) {for (int j = target; j >= nums[i]; j--) {dp[j] = Math.max(dp[j], dp[j - nums[i]] + nums[i]);}}return dp[target] == target;}
1049.最后一块石头的重量II
力扣题目链接
有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
- 如果
x == y,那么两块石头都会被完全粉碎; - 如果
x != y,那么重量为x的石头将会完全粉碎,而重量为y的石头新重量为y-x。
最后,最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下,就返回 0。
输入:stones = [2,7,4,1,8,1]
输出:1
解释:
组合 2 和 4,得到 2,所以数组转化为 [2,7,1,8,1],
组合 7 和 8,得到 1,所以数组转化为 [2,1,1,1],
组合 2 和 1,得到 1,所以数组转化为 [1,1,1],
组合 1 和 1,得到 0,所以数组转化为 [1],这就是最优值。
解题思路
- dp[target]里是容量为target的背包所能背的最大重量。分成两堆石头,一堆石头的总重量是dp[target],另一堆就是sum - dp[target]。相撞之后剩下的最小石头重量就是 (sum - dp[target]) - dp[target]。
Java实现
class Solution_LC1049 {public int lastStoneWeightII(int[] stones) {int sum = 0;for (int i : stones) {sum += i;}int target = sum >> 1;//初始化dp数组int[] dp = new int[target + 1];for (int i = 0; i < stones.length; i++) {//采用倒序for (int j = target; j >= stones[i]; j--) {//两种情况,要么放,要么不放dp[j] = Math.max(dp[j], dp[j - stones[i]] + stones[i]);}}return sum - 2 * dp[target];}
}
494.目标和
力扣题目链接
给你一个整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 '+' 或 '-' ,然后串联起所有整数,可以构造一个 表达式 :
- 例如,
nums = [2, 1],可以在2之前添加'+',在1之前添加'-',然后串联起来得到表达式"+2-1"。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目。
输入:nums = [1,1,1,1,1], target = 3
输出:5
解释:一共有 5 种方法让最终目标和为 3 。
-1 + 1 + 1 + 1 + 1 = 3
+1 - 1 + 1 + 1 + 1 = 3
+1 + 1 - 1 + 1 + 1 = 3
+1 + 1 + 1 - 1 + 1 = 3
+1 + 1 + 1 + 1 - 1 = 3
解题思路
- 数组集合可以分为正数集合和负数集合,正+负=sum,正-负=target,题目可以转化为求sum=正数的子集合的个数。
- 纯01背包问题:装满背包最大的价值是多少;分割等和子集,能不能装满这个背包;最后一块石头的重量,给定背包,能装多少装多少;目标和:装满这个背包有多少方法?
- dp数组的含义:填满j(包括j)这么大容积的包,有dp[j]种方法。
- dp[j]=dp[j-nums[i]]的累加。比如nums[i]=2,dp[5]+=dp[5-nums[i]]。
Java实现
class Solution_LC494 {public int findTargetSumWays(int[] nums, int target) {int len = nums.length;int sum = 0;for (int i = 0; i < len; i++) {sum += nums[i];}if (target > sum || target < -sum) {return 0;}if ((target + sum) % 2 != 0) {return 0;}int goal = (target + sum) / 2;//填满j(包括j)这么大容积的包,有dp[j]种方法int[] dp = new int[goal + 1];dp[0] = 1;for (int i = 0; i < nums.length; i++) {for (int j = goal; j >= nums[i]; j--) {dp[j] += dp[j - nums[i]];}}return dp[goal];}
}
二维数组的实现
class Solution {public int findTargetSumWays(int[] nums, int target) {int sum = 0;for (int num : nums) {sum += num;}int diff = sum - target;if (diff < 0 || diff % 2 != 0) {return 0;}int n = nums.length, neg = diff / 2;int[][] dp = new int[n + 1][neg + 1];dp[0][0] = 1;for (int i = 1; i <= n; i++) {int num = nums[i - 1];for (int j = 0; j <= neg; j++) {dp[i][j] = dp[i - 1][j];if (j >= num) {dp[i][j] += dp[i - 1][j - num];}}}return dp[n][neg];}
}
474.一和零
力扣题目链接
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。
输入:strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
输出:4
解释:最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ,因此答案是 4 。
其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意,因为它含 4 个 1 ,大于 n 的值 3 。
解题思路
dp[i][j]表示i个0和j个1时的最大子集
Java实现
class Solution {public int findMaxForm(String[] strs, int m, int n) {int[][] dp = new int[m + 1][n + 1];for (String str : strs) {int zeroNum = 0;int oneNum = 0;for (int i = 0; i < str.length(); i++) {if (str.charAt(i) == '0') {zeroNum++;} else {oneNum++;}}for (int i = m; i >= zeroNum; i--) {for (int j = n; j >= oneNum; j--) {dp[i][j] = Math.max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);}}}return dp[m][n];}
}
总结一下
纯 0 - 1 背包 是求 给定背包容量 装满背包 的最大价值是多少。
416. 分割等和子集 是求 给定背包容量,能不能装满这个背包。
1049. 最后一块石头的重量 II 是求 给定背包容量,尽可能装,最多能装多少
494. 目标和 是求 给定背包容量,装满背包有多少种方法。
本题是求 给定背包容量,装满背包最多有多少个物品。

相关文章:

【算法系列之动态规划III】背包问题
背包问题 01背包指的是物品只有1个,可以选也可以不选。完全背包是物品有无数个,可以选几个也可以不选。 二维数组01背包 有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次&…...

MONAI-LayerFactory设计与实现
LayerFactory 用于创建图层的工厂对象,这使用给定的工厂函数来实际产生类型或构建可调用程序。这些函数是通过名称来参考的,可以在任何时候添加。 用到的关键技术点: 装饰器(Decorators), 例如:property装饰器,创建…...

Thinkphp 6.0路由的定义
本节课我们来了解一下路由方面的知识,然后简单的使用一下路由的功能。 一.路由简介 1. 路由的作用就是让 URL 地址更加的规范和优雅,或者说更加简洁; 2. 设置路由对 URL 的检测、验证等一系列操作提供了极大的便利性; …...

Kafka系列之:深入理解Kafka集群调优
Kafka系列之:深入理解Kafka集群调优 一、Kafka硬件配置选择二、Kafka内存选择三、CPU选择四、网络选择五、生产者调优六、broker调优七、消费者调优八、Kafka总体调优一、Kafka硬件配置选择 服务器台数选择: 2 * (生产者峰值生产速率 * 副本数 / 100) + 1磁盘选择: Kafka…...

creator-泄漏检测之资源篇
title: creator-泄漏检测之资源篇 categories: Cocos2dx tags: [creator, 优化, 泄漏, 内存] date: 2023-03-29 14:48:48 comments: false mathjax: true toc: true creator-泄漏检测之资源篇 前篇 资源释放 - https://docs.cocos.com/creator/manual/zh/asset/release-manager…...
)
【DevOps】Jenkins 运行任务时遇到 FATAL:Unable to produce a script file 报错(已解决)
文章目录一、问题描述二、定位原因三、解决方案四、其他方案五、总结关键词: Jenkins、Unable to produce a script file、UnmappableCharacterException、IOException: Failed to create a temp file on一、问题描述 由于使用的 Jenkins 存在安全漏洞(…...

Web前端
WEB前端 HTMLCSSJavaScriptjQuery(js框架)Bootstrap(CSS框架)AJAXJSON 文章目录 WEB前端WEB前端三大核心技术Web开发工具文本编辑器集成开发环境(IDE)浏览器选择HTML什么是 HTML?HTML版本变迁HTML-HelloWorldHTML 文档 = 网页HTML 标签属性(Attribute)HTML 常用标签...
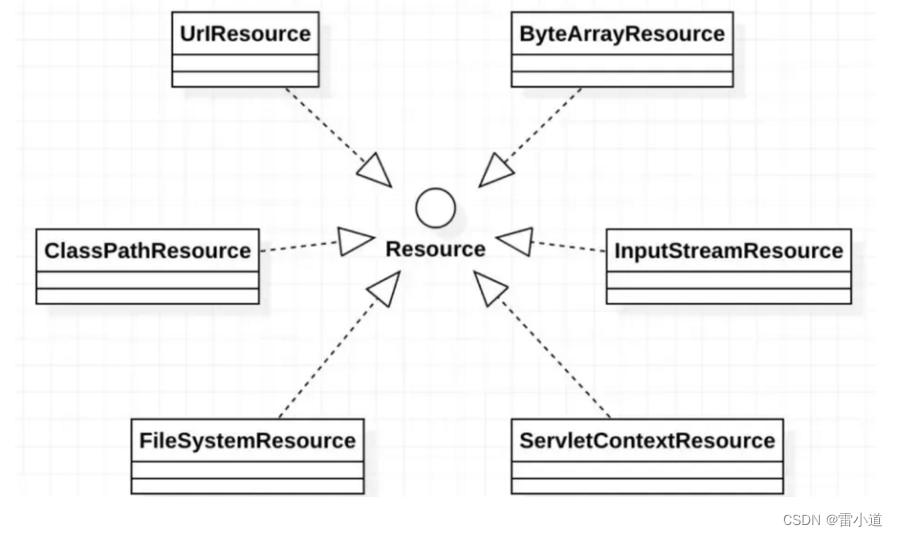
资源操作:Resources
文章目录1. Spring Resources概述1.2 Resource 接口1.3 Resource的实现类1.3.1 UrlResource访问网络资源1.3.2 ClassPathResource访问类路径下资源1.3.3 FileSystemResource访问文件系统资源1.3.4 ServletContextResource1.3.5、InputStreamResource1.3.6、ByteArrayResource1.…...
GDB调试的学习
很早就想在好好学一学gdb了,正好最近学算法(以前一直以为干硬件不需要什么特别厉害的算法,结果现在卷起来了。大厂面试题也有复杂一些的算法了) 下面的这些命令是别的博主总结的 GDB 调试过程_gdb调试过程_麷飞花的博客-CSDN博客…...
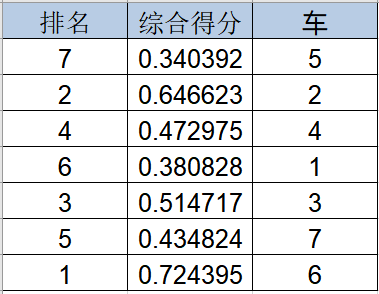
熵值法综合评价分析流程
熵值法综合评价分析流程 一、案例背景 当前有一份数据,是各品牌车各个维度的得分情况,现在想要使用熵值法进行综合评价,得到各品牌车的综合得分,从而进行车型优劣对比,为消费者提供购车依据。 数据如下(数…...

使用Python Pandas库操作Excel表格的技巧
在数据分析和处理中,我们经常需要对Excel表格进行操作。Python Pandas库提供了丰富的API来读取、写入、修改Excel表格。本文将介绍如何使用Python Pandas库操作Excel表格,包括向Excel表格添加新行、创建Excel表格等。 1.向Excel表格添加新行 下面是一个…...
LeetCode练习七:动态规划上:线性动态规划
文章目录一、 动态规划基础知识1.1 动态规划简介1.2 动态规划的特征1.2.1 最优子结构性质1.2.2 重叠子问题性质1.2.3 无后效性1.3 动态规划的基本思路1.4 动态规划基础应用1.4.1 斐波那契数1.4.2 爬楼梯1.4.3 不同路径1.5 个人总结二、记忆化搜索2.1 记忆化搜索简介2.2 记忆化搜…...

基于正点原子F407开发版和SPI接口屏移植touchgfx完整教程(一)
一、相关软件包安装 1、打开cubemx包管理器 2、安装F4软件包 3、安装touchgfx软件包 二、工程配置 1、新建工程 2、sys配置 3、rcc配置 4、crc配置 5、添加touchgfx软件包 6、配置touchgfx软件包 将width和height改为自己屏幕尺寸 7、生成工程 三、代码修改 1、将屏幕相关驱…...

Linux--进程间通信
前言 上一篇相关Linux文章已经时隔2月,Linux的学习也相对于来说是更加苦涩;无妨,漫漫其修远兮,吾将上下而求索。 下面该片文章主要是对进程间通信进行介绍,还对管道,消息队列,共享内存,信号量都…...

hadoop伪分布式集群搭建
基于hadoop 3.1.4 一、准备好需要的文件 1、hadoop-3.1.4编译完成的包 链接: https://pan.baidu.com/s/1tKLDTRcwSnAptjhKZiwAKg 提取码: ekvc 2、需要jdk环境 链接: https://pan.baidu.com/s/18JtAWbVcamd2J_oIeSVzKw 提取码: bmny 3、vmware安装包 链接: https://pan.baidu…...

Qt 中的信息输出机制:QDebug、QInfo、QWarning、QCritical 的简单介绍和用法
Qt 中的信息输出机制介绍QDebug在 Qt 中使用 qDebug输出不同类型的信息浮点数:使用 %!f(MISSING) 格式化符号输出浮点数布尔值:使用 %! (MISSING)和 %! (MISSING)格式化符号输出布尔值对象:使用 qPrintable() 函数输出对象的信息qInfoqWarnin…...

C++读写excel文件的的第三方库
一、比较流行的库 1. OpenXLSX 用于读取、写入、创建和修改 Microsoft Excel (.xlsx) 文件的 C 库。 2. xlnt xlnt 是一个现代 C 库,用于操作内存中的电子表格以及从 XLSX 文件读取/写入它们,如ECMA 376 第 4 版中所述。xlnt 1.0 版的首次公开发布是在 …...
【关于Linux中----多线程(一)】
文章目录认识线程创建线程线程优点和缺点创建一批线程终止线程线程的等待问题认识线程 在一个程序里的一个执行路线就叫做线程(thread)。更准确的定义是:线程是“一个进程内部的控制序列”一切进程至少都有一个执行线程线程在进程内部运行&a…...

2023年全国最新安全员精选真题及答案34
百分百题库提供安全员考试试题、建筑安全员考试预测题、建筑安全员ABC考试真题、安全员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 11.(单选题)物料提升机附墙架设置要符合设计要求,但…...

数据出境是什么意思?我国数据出境合规要求是什么?
随着经济全球化深入以及云计算等技术的发展,数据在全球范围跨境流动。数据跨境在促进经济增长、加速创新的同时,对数据主权、数据权属、个人信息保护等一系列问题逐渐浮出水面。今天我们就先来了解一下数据出境是什么意思?我国数据出境合规要…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...
