(done) 使用泰勒展开证明欧拉公式
问问神奇的 GPT，how to prove euler formula? 一个答案如下：
相关文章：
(done) 使用泰勒展开证明欧拉公式
问问神奇的 GPT，how to prove euler formula? 一个答案如下：...
红队apt--邮件钓鱼
前言 欢迎来到我的博客 个人主页:北岭敲键盘的荒漠猫-CSDN博客 免责声明: 本文仅供了解攻击方手法使用，切勿用于非授权情节 初步了解邮件基础 用途方面 这个我们应该比较熟悉，最常用于验证码接收，也有一些厂商会用这个来打广告，…...
十七，Spring Boot 整合 MyBatis 的详细步骤(两种方式)
十七，Spring Boot 整合 MyBatis 的详细步骤(两种方式) 文章目录 十七，Spring Boot 整合 MyBatis 的详细步骤(两种方式)1. Spring Boot 配置 MyBatis 的详细步骤2. 最后： MyBatis 的官方文档：https://mybatis.p2hp.com/ 关于 MyBa…...
DNS协议解析
DNS协议解析 什么是DNS协议 IP地址：一长串唯一标识网络上的计算机的数字 域名：一串由点分割的字符串名字 网址包含了域名 DNS：域名解析协议 IP>域名 --反向解析 域名>IP --正向解析 域名 由ICANN管理，有级别…...
每日一题——第一百零八题
题目： 写几个函数， ①输入10个职工的姓名和职工号 ②按照职工号由小到大排列， 姓名顺序也随之调整 ③要求输入一个职工号， 用折半查找找出该职工的姓名 #include<stdio.h> #include<string.h> #define MAX_EMPOLYEES…...
使用Python免费将pdf转为docx
刚刚想将pdf转换为docx文档时，居然要收费 还好我学过编程，这不得露两手 将pdf 转换为 docx 文档 的操作步骤 我这里使用的是Python语言 （1）在终端上安装 pdf2docx 是一个 Python 库，它可以将 PDF 文件转换为 Word (…...
树莓派4B+UBUNTU20.04+静态ip+ssh配置
树莓派4B+UBUNTU20.04+静态ip+ssh配置 1.烧录Ubuntu镜像1.1选择pi 4b1.2选择ubuntu server (服务器版，无桌面)20.041.3选择sd卡1.4 点击右下角 NEXT ，编辑设置，输入密码，wifi选CN, 开启ssh1.5 烧录，依次点击“是”，等待完成2 烧录完成后装入树莓派，上电，等待系统完成配…...
C#实现指南:将文件夹与exe合并为一个exe
在软件开发过程中，有时需要将多个文件（如资源文件、配置文件等）与可执行文件（exe）打包在一起，以便于分发和部署。在C#中，我们可以利用ILMerge或Costura.Fody等工具来实现这一目标。本文将介绍如…...
linux信号 | 学习信号三步走 | 全解析信号的产生方式
前言：本节内容是信号， 主要讲解的是信号的产生。信号的产生是我们学习信号的第二个阶段。 我们已经学习过第一个阶段——信号的概念与预备知识（没有学过的友友可以查看我的前一篇文章）。 以及我们还没有学习信号的第三个阶段——信…...
C++ 刷题 使用到的一些有用的容器和函数
优先队列 c优先队列priority_queue（自定义比较函数）_c优先队列自定义比较-CSDN博客 373. 查找和最小的 K 对数字 - 力扣（LeetCode） 官方题解： class Solution { public:vector<vector<int>> kSmallestP…...
【Kubernetes】常见面试题汇总（三十四）
目录 86. K8s 每个 Pod 中有一个特殊的 Pause 容器能否去除，简述原因。 特别说明： 题目 1-68 属于【Kubernetes】的常规概念题，即 “ 汇总（一）~（二十二）” 。 题目 69-113 属于【Kuberne…...
C++标准库双向链表 list 中的insert函数实现。
CPrimer中文版（第五版）： //运行时错误：迭代器表示要拷贝的范围，不能指向与目的位置相同的容器 slist.insert(slist.begin(),slist.begin(),slist.end()); 如果我们传递给insert一对迭代器，它们不能…...
)
华为机考练习(golang)
输入 第一行输入一个正整数N，表示整数个数。（0<N<100000） 第二行输入N个整数，整数的取值范围为[-100,100]。 第三行输入一个正整数M，M代表窗口的大小，M<100000，且M<N。 输出 窗口…...
51单片机快速入门之按键应用拓展
51单片机快速入门之按键应用拓展 LED的点动控制: 循环检测,当key 为0 时 led 亮 反之为熄灭 while(1){ if(key!1) { led0; }else { led1; } } LED的锁定控制: 当按钮按下,led取反值 while(1) { if(key!1) { led!led; } } LED的4路抢答控制: bz默认为0 !bz 取反值,循环启动…...
数据库 - MySQL的事务
目录 前言 一、事务的特性 （一）原子性 （二）一致性 （三）隔离性 （四）持久性 二、事务的控制语句 三、事务隔离级别 （一）读未提交 （二&…...
【Python机器学习】NLP信息提取——提取人物/事物关系
目录 词性标注 实体名称标准化 实体关系标准化和提取 单词模式 文本分割 断句 断句的方式 使用正则表达式进行断句 词性标注 词性（POS）标注可以使用语言模型来完成，这个语言模型包含词及其所有可能词性组成的字典。然后，该…...
vector类
一、STL库 vector 1.1 vector的介绍 vector英文意思为向量：向量是表示大小可以改变的数组的序列容器。 指向其元素的常规指针上的偏移量来访问其元素，并且与数组中的效率一样高。但与数组不同，它们的大小可以动态变化，其存储由容…...
python常见的魔术方法
什么是魔术方法 Python类的内置方法，各自有各自的特殊功能，被称之为魔术方法 常见的魔术方法有以下： __init__:构造方法 __str__:字符串方法 __lt__:小于、大于符号比较 __le__:小于等于、大于等于符合比较 __eq__:等于符合比较__init__ c…...
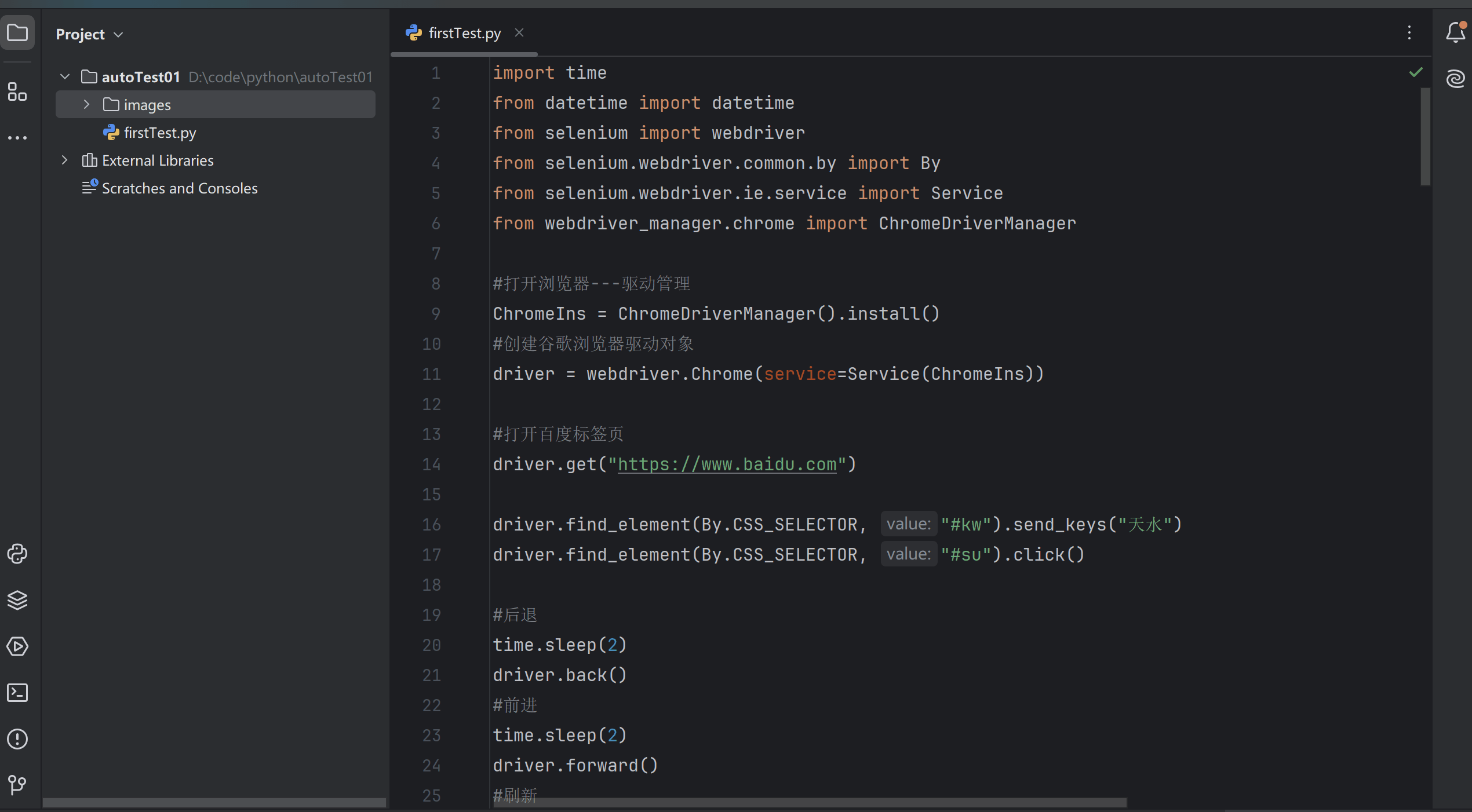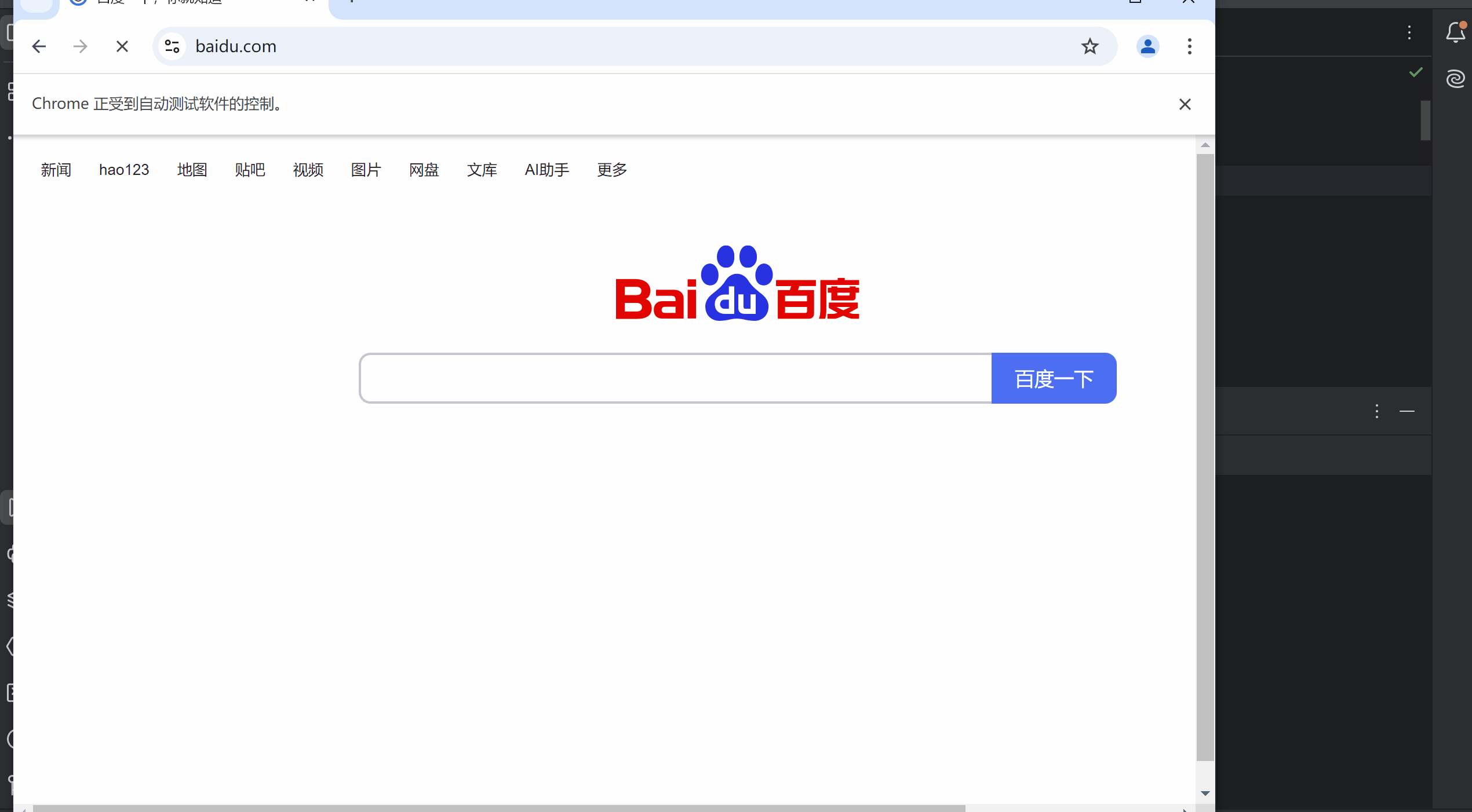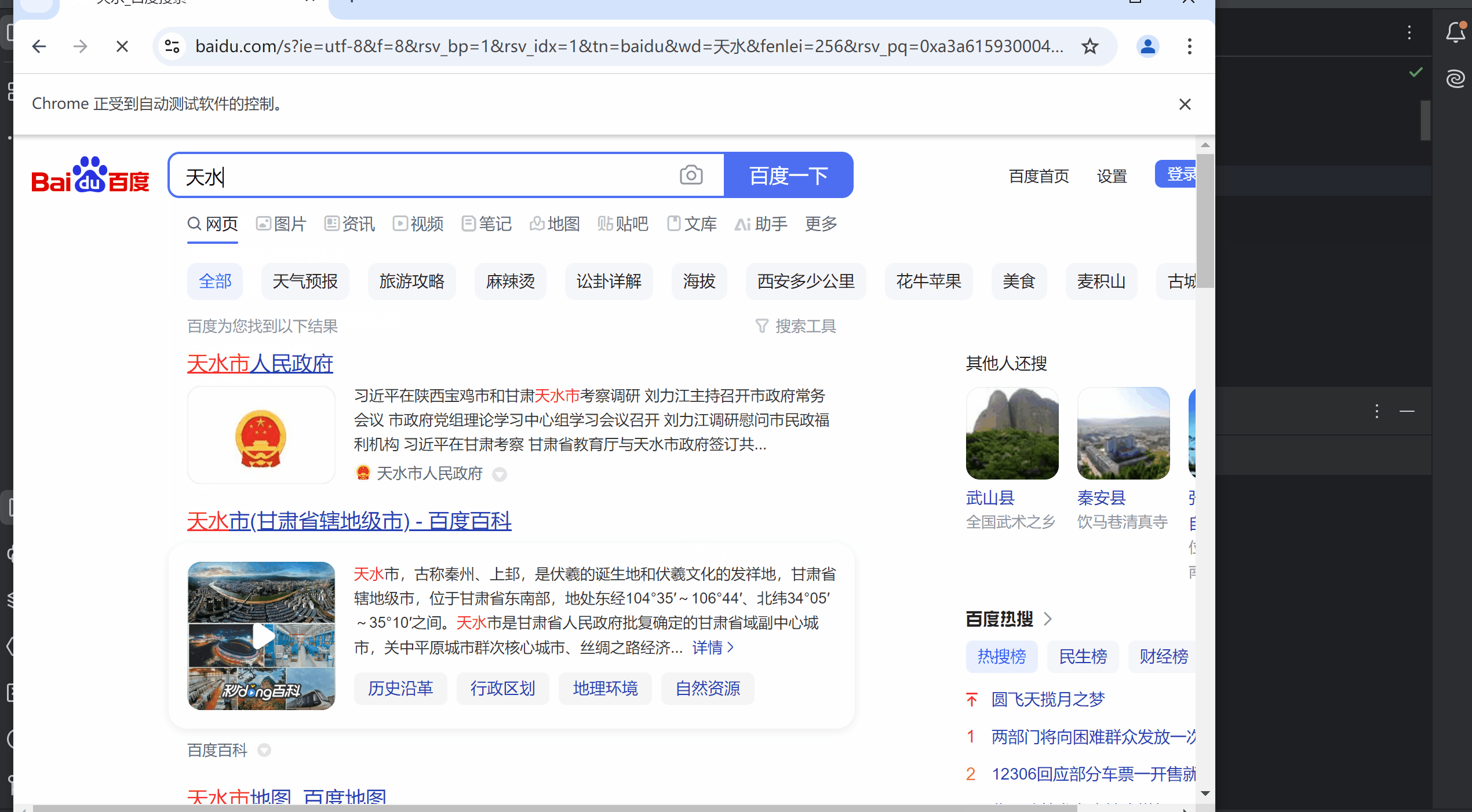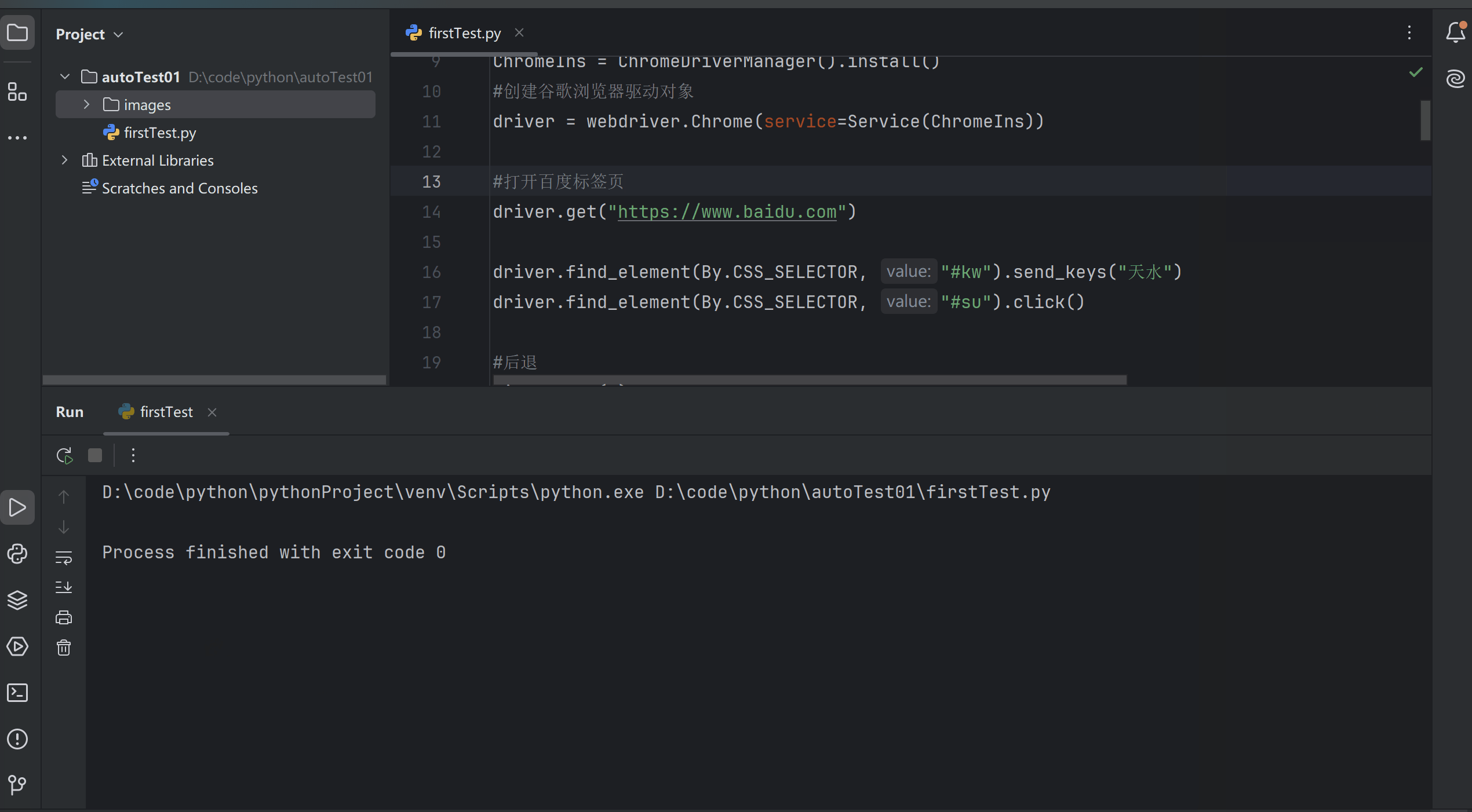
自动化测试常用函数：弹窗、等待、导航、上传与参数设置
目录 一、弹窗 1. 警告弹窗确认弹窗 2. 提示弹窗 二、等待 1. 强制等待 2. 隐式等待 3. 显示等待 三、浏览器导航 1. 打开网站 2. 浏览器的前进、后退、刷新 四、文件上传 五、浏览器参数设置 1. 设置无头模式 2. 页面加载策略 一、弹窗 弹窗是在页面是找不到任何…...
【必看】2024国赛选题分布情况分析及数模国赛答辩指南~答辩不走弯路
↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑ 紧张刺激的数模国赛已经过去一段时间，各赛区的成绩发布也在陆续进…...
测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”，无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息： 关注测试号：扫二维码关注测试号。 发送模版消息： import requests da…...
CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框，很难让人不联想到SQL注入，但提示都说了不是SQL注入，所以就不往这方面想了 先查看一下网页源码，发现一段JavaScript代码，有一个关键类ctfs…...
脑机新手指南（八）：OpenBCI_GUI：从环境搭建到数据可视化（下）
一、数据处理与分析实战 （一）实时滤波与参数调整 基础滤波操作 60Hz 工频滤波：勾选界面右侧 “60Hz” 复选框，可有效抑制电网干扰（适用于北美地区，欧洲用户可调整为 50Hz）。 平滑处理&…...
day52 ResNet18 CBAM
在深度学习的旅程中，我们不断探索如何提升模型的性能。今天，我将分享我在 ResNet18 模型中插入 CBAM（Convolutional Block Attention Module）模块，并采用分阶段微调策略的实践过程。通过这个过程，我不仅提升…...
AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接：A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串，只有在同时为 o 时输出 Yes 并结束程序，否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...
【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装；只需暴露 19530（gRPC）与 9091（HTTP/WebUI）两个端口，即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...
镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户，但你不希望用 root 权限运行 ns-3（这是对的，ns3 工具会拒绝 root），你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案：创建非 roo…...
鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装： 下载安装DevEco Studio 4.0（支持HarmonyOS 5）配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化： ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...
C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...
OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波（Mean Shift Filtering）函数meanShiftFiltering()
操作系统：ubuntu22.04 OpenCV版本：OpenCV4.9 IDE:Visual Studio Code 编程语言：C11 算法描述 在 GPU 上对图像执行 均值漂移滤波（Mean Shift Filtering），用于图像分割或平滑处理。 该函数将输入图像中的…...