1.2 HuggingFists安装说明-Linux安装
Linux版安装说明
下载地址
【GitHub】https://github.com/Datayoo/HuggingFists
【百度网盘】https://pan.baidu.com/s/12-qzxARjzRjYFvF8ddUJQQ?pwd=2024
安装说明
环境要求
操作系统:CentOS7
硬件环境:至少4核8G,系统使用Containerd容器,容器以及镜像会固定存放到/data目录下

安装步骤
-
从git上拉取工程文件 git clone https://github.com/Datayoo/HuggingFists
-
, 或者直接使用download zip下载。(中国国内访问github较慢的朋友,可以通过国内网盘进行下载)。需要注意的是,当使用Windows操作系统克隆项目时,Linux脚本文件中的'\n'会被替换为'\r\n'。当拷贝项目到Linux系统下时,由于'\n'的不同,脚本会无法执行。使用IDEA的开发者可以参考配置 Git 处理行结束符解决问题。
-
进入sengee.community.linux。未安装docker的,执行安装脚本 bash install.sh,会自动安装containerd。已经安装docker的,可以执行bash install_for_docker.sh
-
脚本执行结束后,可通过curl http://localhost:38172 测试系统是否正确安装。安装结束后,可通过访问url地址:“http://服务器IP:38172” 打开工具使用界面。如果外部无法访问到页面,可以将服务器重启一次再试,算子平台会开机自启!

使用Docker安装
linux版本下可以查看install.sh文件,文件中的命令基于centos7编写,ubuntu用户需要自行调整
主要步骤如下:
1.创建datayoo用户
adduser datayoo
2.修改权限,因为容器使用datayoo用户运行
chown -R datayoo:datayoo ../sengee.community.linux/*
chmod -R 777 ../sengee.community.linux/*
3。合并镜像文件,因为镜像文件超过50M,分发安装包时镜像文件被拆分了
cat ./images/mysql.tar.gz* > ./images/mysql.tar.gz
cat ./images/sengee.tar.gz* > ./images/sengee.tar.gz
4.加载镜像文件
docker load -i ./images/mysql.tar.gz
docker load -i ./images/nginx.tar.gz
docker load -i ./images/sengee.tar.gz
5.启动服务
docker compose up -d
6.等几分钟,服务器上通过curl localhost:38172可以访问到页面
相关文章:

1.2 HuggingFists安装说明-Linux安装
Linux版安装说明 下载地址 【GitHub】https://github.com/Datayoo/HuggingFists 【百度网盘】https://pan.baidu.com/s/12-qzxARjzRjYFvF8ddUJQQ?pwd2024 安装说明 环境要求 操作系统:CentOS7 硬件环境:至少4核8G,系统使用Containerd…...

四,MyBatis-Plus 当中的主键策略和分页插件的(详细实操使用)
四,MyBatis-Plus 当中的主键策略和分页插件的(详细实操使用) 文章目录 四,MyBatis-Plus 当中的主键策略和分页插件的(详细实操使用)1. 主键策略1.1 主键生成策略介绍 2. 准备工作:2.1 AUTO 策略2.2 INPUT 策略2.3 ASSIGN_ID 策略2.3.1 雪花算…...
Win32打开UWP应用
最近无意间发现Windows里一个神奇的文件夹。 shell:appsfolder 运行打开 这个文件夹后,你可以看到本机安装的所有应用程序。 我觉得这个挺方便的,所以做了一个简单的appFolderDialog包给C#用 项目地址:https://github.com/TianXiaTech/App…...

C# C++ 笔记
第一阶段知识总结 lunix系统操作 1、基础命令 (1)cd cd /[目录名] 打开指定文件目录 cd .. 返回上一级目录 cd - 返回并显示上一次目录 cd ~ 切换到当前用户的家目录 (2)pwd pwd 查看当前所在目录路径 pwd -L 打印当前物理…...

关于最小二乘法
最小二乘法的核心思想简单而优雅:我们希望找到一条最佳的曲线,使其尽可能贴近所有的数据点。想象一下,当你在画布上描绘一条线,目标是让这条线与点的距离最小。数学上,这可以表示为: 在这个公式中ÿ…...

国产OpenEuler与Centos全面之比较
OpenEuler 和 CentOS 都是流行的 Linux 发行版,但它们有一些关键的区别。以下是 OpenEuler 和 CentOS 的全面比较: 1. 起源和支持: - OpenEuler:由华为公司支持,中国开源社区主导开发的操作系统,旨在构建一…...

Java面试题一
一、Java语言有哪些特性? Java语言具有多种特性,这些特性使得Java成为一种广泛使用的编程语言。以下是Java语言的一些主要特性: 面向对象(Object-Oriented): Java是一种纯面向对象的编程语言。它支持类&…...
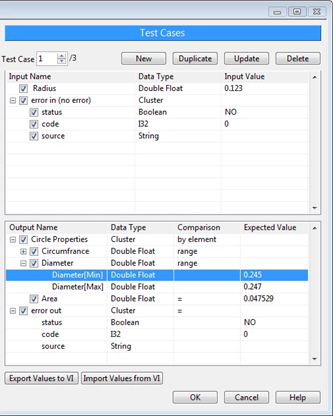
LabVIEW提高开发效率技巧----自动化测试和持续集成
在大型项目中,自动化测试和持续集成是提高开发效率和代码质量的关键手段。通过这些技术,开发者能够在开发的早期阶段快速发现问题,减少后期调试的工作量,并且能够确保代码的稳定性和可维护性。以下是这两个概念如何在LabVIEW开发中…...

开源链动 2+1 模式 S2B2C 商城小程序:激活 KOC,开启商业新征程
摘要:本文深入探讨了 KOC 在立体连接中的重要性,以及如何通过开源链动 21 模式 S2B2C 商城小程序发现和找到更多的 KOC。强调了历史积累强关系和快速强化强关系的方法,并阐述了该商城小程序在推动商业发展中的关键作用。 一、引言 在当今竞争…...

什么是Node.js?
为什么JavaScript可以在浏览器中被执行? 在浏览器中我们加载了一些待执行JS代码,这些字符串要当中一个代码去执行,是因为浏览器中有JavaScript的解析引擎,它的存在我们的代码才能被执行。 不同的浏览器使用不同的javaScript解析引…...

即插即用篇 | DenseNet卷土重来! YOLOv8 引入全新密集连接卷积网络 | ECCV 2024
本改进已同步到YOLO-Magic框架! 本文重新审视了密集连接卷积网络(DenseNets),并揭示了其在主流的ResNet风格架构中被低估的有效性。我们认为,由于未触及的训练方法和传统设计元素没有完全展现其能力,DenseNets的潜力被忽视了。我们的初步研究表明,通过连接实现的密集连接…...
智能监控,守护绿色能源:EasyCVR在电站视频监控中心的一站式解决方案
随着科技的飞速发展,视频监控技术在社会安全、企业管理及智慧城市建设等领域中扮演着越来越重要的角色。特别是在电力行业中,电站作为能源供应的关键设施,其安全性和稳定性至关重要。传统的人工监控方式已难以满足现代电站复杂多变的运行需求…...

【BUG】静读天下|静读天下无法设置段间距解决方案
【BUG】静读天下|静读天下无法设置段间距解决方案 文章目录 【BUG】静读天下|静读天下无法设置段间距解决方案前言解决办法 凑质量分静读天下的特点与优势功能布局与使用技巧个人使用心得结语 前言 03-23 求助|关于排版的问题【静读天下吧】_…...

希捷电脑硬盘好恢复数据吗?探讨可能性、方法以及注意事项
在数字化时代,数据已成为我们生活和工作中不可或缺的一部分。希捷电脑硬盘作为数据存储的重要设备,承载着大量的个人文件、工作资料以及珍贵回忆。然而,面对硬盘故障或误操作导致的数据丢失,许多用户不禁要问:希捷电脑…...

java通过webhook给飞书发送群消息
现在使用飞书的人越来越多了,飞书有一个最大的好处,可以使用webhook简便的发送群消息。而在工作中,也经常会因为一些运维方面的工作,需要给飞书发送群消息,来实时提醒相关负责人,及时处理工作。 一、先看一下效果吧&a…...

每日一题——第一百零九题
题目:进制转换合集。任意r进制与十进制之间的转换 #include<stdio.h> #include<stdlib.h> #include<string.h> #include<ctype.h> long stringToDecimal(const char* str, int base); void convertToBaseR(int num, int r);int main() {ch…...

街头摊贩检测系统源码分享
街头摊贩检测检测系统源码分享 [一条龙教学YOLOV8标注好的数据集一键训练_70全套改进创新点发刊_Web前端展示] 1.研究背景与意义 项目参考AAAI Association for the Advancement of Artificial Intelligence 项目来源AACV Association for the Advancement of Computer Vis…...

服务器数据恢复—SAN环境下LUN映射出错导致文件系统一致性出错的数据恢复案例
服务器数据恢复环境: SAN环境下一台存储设备中有一组由6块硬盘组建的RAID6磁盘阵列,划分若干LUN,MAP到不同业务的SOLARIS操作系统服务器上。 服务器故障: 用户新增了一台服务器,将存储中的某个LUN映射到新增加的这台服…...

深度学习:自然语言处理的基本原理
概念: 自然语言处理(Natural Language Processing,简称NLP)是人工智能和语言学领域的一个分支,它致力于研究如何让计算机能够理解、解释和生成人类语言,以及如何实现人与计算机之间的有效通信。自然语言处理…...

Win10 Chrome浏览器被强制绑定主页的解决办法
Win10 Chrome浏览器被强制绑定主页的解决办法 背景 刚刚重装的系统默认是某杀毒软件,使用浏览器时发现浏览器主页老是hao123,还改不了。于是卸载了此杀毒软件,换了别的。发现还是解决不了浏览器主页被绑定且改不了的问题 体现 chrome://se…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

基于服务器使用 apt 安装、配置 Nginx
🧾 一、查看可安装的 Nginx 版本 首先,你可以运行以下命令查看可用版本: apt-cache madison nginx-core输出示例: nginx-core | 1.18.0-6ubuntu14.6 | http://archive.ubuntu.com/ubuntu focal-updates/main amd64 Packages ng…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...
