2.11 循环赛日程表

- 博主简介:一个爱打游戏的计算机专业学生
- 博主主页: @夏驰和徐策
- 所属专栏:算法设计与分析
目录
书本内容:
我的理解:
更优化的算法:
总结
1.注意实现问题
2.当用C语言和C++实现循环赛日程表算法时,需要注意以下几点:
书本内容:
分治法不仅可以用来设计算法,在其他方面也有广泛应用,如用分治思想来设计电路、
构造数学证明等。现举例说明。
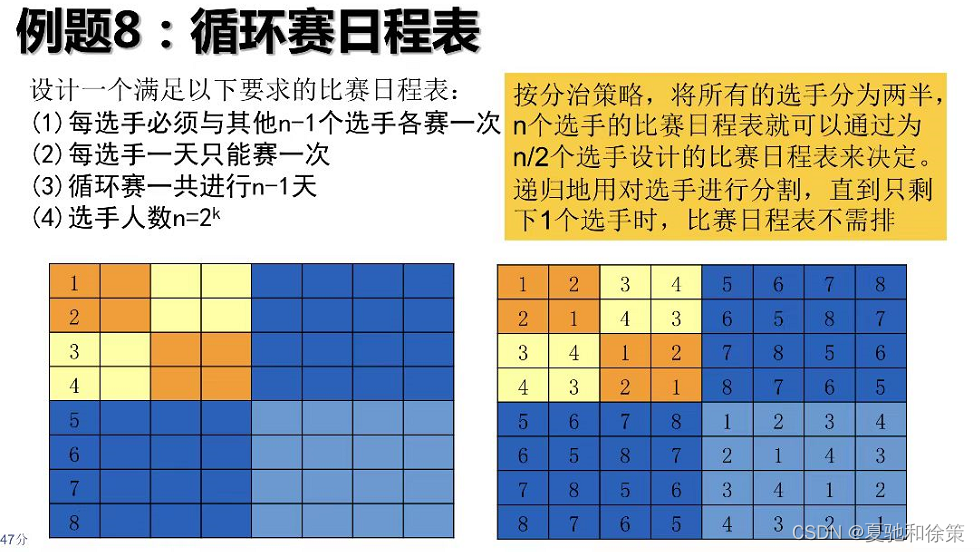
设有1-2*个运动员要进行网球循环赛。现要设计一个满足以下要求的比赛日程表:
① 每个选手必须与其他 n-1 个选手各赛一次;
② 每个选手一天只能赛一次;
③ 循环赛一共进行 n-1 天;
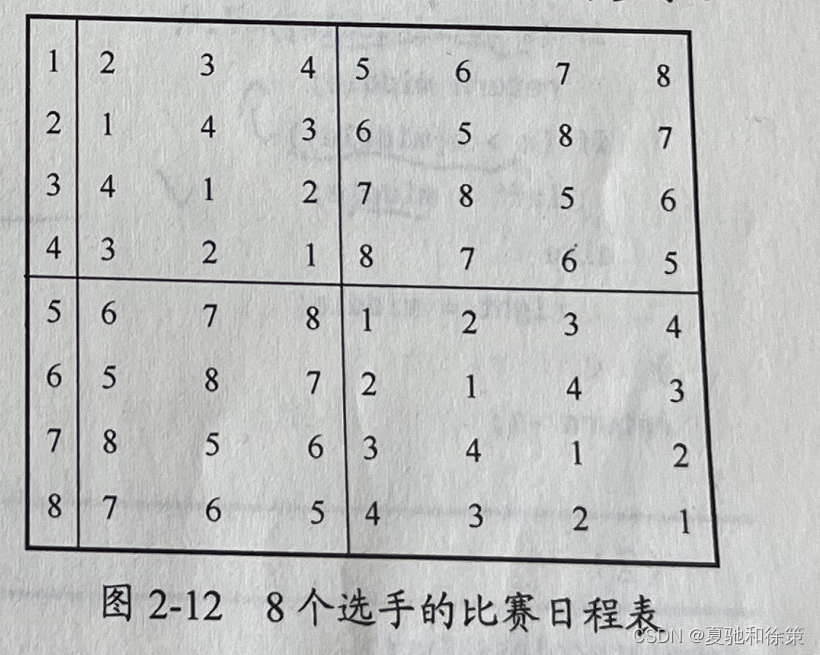
按此要求可将比赛日程表设计成有n行和n-1 列的表。在表中第之行和第j列处填入第i个选手在第;天所遇到的选手。按分治策略,可以将所有选手对分为两半,n个选手的比赛日程表就可以通过为1/2个选手设计的比赛日程表来決定。递归地用这种一分为二的策略对选手进行分割,直到只剩下两个选手时,比赛日程表的制定就变得简单了。这时只要让这两个选手进行比赛就可以了。图 2-12 所列出的正方形表是8个选手的比赛日程表。其中,左上角与左下角的两小块分别为选手 1至选手4 和选手 5至选手8 前了天的比赛日程。据此将左上角小块中的所有数字按其相对位置抄到右下角,将左下角小块中的所有数字按其相对位置挱到右5上角,这样就分别安排好了选手 1至选手 4 和选手 5至选手8在后 4 天的比赛日程。依此思想,容易将这2个比赛日程表推广到具有任意多个选手的情形。在一般情况下,算法可描述如下:
void Table(int k,int **a)
{int n=1;for(int i=1;i<=k;i++){n*=2;}for(int i=1;i<=n;i++){a[1][i]=i;}int m=1;for(int s=1;s<=k;s++){n/=2;for(int i=m+1;i<=2*m;i++){for(int j=m+1;j<=2*m;j++){a[i][j+(t-1)*m*2]=a[i-m][j+t-1*m*2-m];a[i][j+(t-1)*m*2-m]=a[i-m][j+(t-1)*m*2];}}}m*=2;}我的理解:
循环赛日程表的构建可以用递归的分治算法来实现。具体地,将所有参赛队伍按照一定规则划分为两个子集,分别构建它们的日程表,最后将这两个日程表组合起来形成总的日程表。这个过程可以递归地进行,直到日程表中只剩下两个队伍时结束。
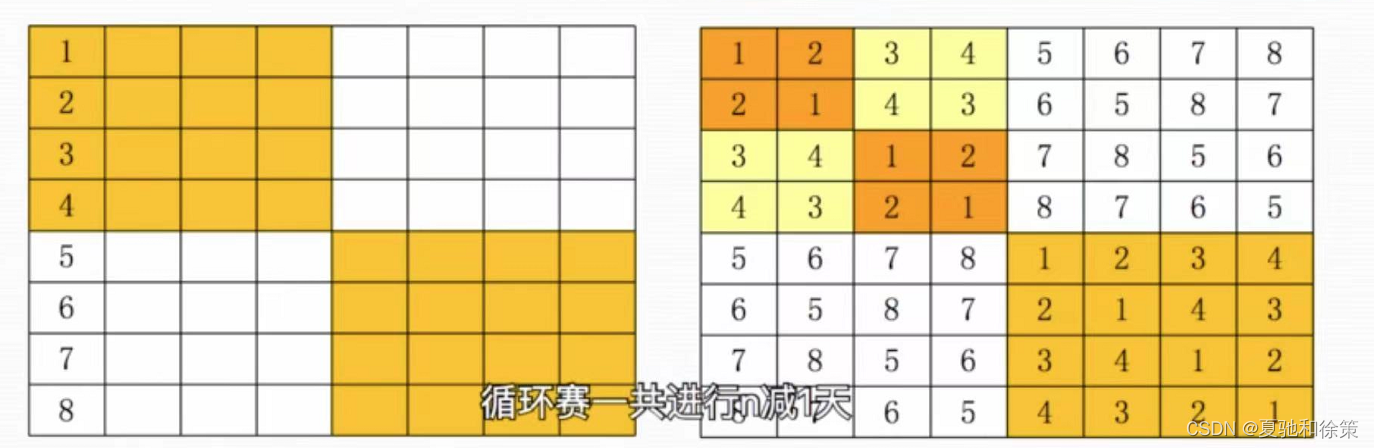
具体来说,可以采用如下的划分方式:将所有队伍分成两组,每组的大小相等或者相差不超过1。接下来,将第一组中的第i个队伍与第二组中的第i个队伍进行比赛,i从1到第一组队伍数目。这样就完成了一个轮次的比赛。然后,将第一组中的所有队伍沿着一个方向循环移动一位,将第二组中的所有队伍沿着相反的方向循环移动一位,得到新的一轮比赛。重复上述步骤直到完成n-1轮比赛,其中n为队伍的总数。这样就得到了完整的循环赛日程表。
在实现分治算法时,需要注意一些细节。例如,在划分队伍时,如果队伍的数目是奇数,需要将一个队伍暂时放到一边,等到下一轮再加入其中一个小组中。在组合两个子日程表时,需要注意将每个队伍在两个子日程表中的比赛分别放到总日程表中对应位置上。此外,还需要适当处理递归终止的情况。
循环赛日程表的构建是一个非常实用的算法问题,因为循环赛日程表在体育比赛、赛车比赛等领域有广泛的应用。采用分治算法可以降低算法的时间复杂度,提高算法的效率。
我的代码实现:
C语言实现:
#include <stdio.h>
#include <stdlib.h>void roundRobinSchedule(int n, int** schedule) {if (n == 1) {schedule[0][0] = 0;return;}int** subSchedule = (int**)malloc((n / 2) * sizeof(int*));for (int i = 0; i < n / 2; i++) {subSchedule[i] = (int*)malloc((n / 2 - 1) * sizeof(int));}roundRobinSchedule(n / 2, subSchedule);for (int i = 0; i < n / 2; i++) {for (int j = 0; j < n - 1; j++) {int team1 = subSchedule[i][j % (n / 2)] + (j / (n / 2)) * (n / 2);int team2 = (n - 1) - subSchedule[i][j % (n / 2)] + (j / (n / 2)) * (n / 2);schedule[team1][i] = team2;schedule[team2][i] = team1;}}if (n % 2 == 1) {for (int i = 0; i < n - 1; i++) {schedule[n - 1][i] = i;schedule[i][n - 1] = n - 1 - i;}}for (int i = 0; i < n / 2; i++) {free(subSchedule[i]);}free(subSchedule);
}int main() {int n = 6;int** schedule = (int**)malloc(n * sizeof(int*));for (int i = 0; i < n; i++) {schedule[i] = (int*)malloc((n - 1) * sizeof(int));}roundRobinSchedule(n, schedule);for (int i = 0; i < n; i++) {for (int j = 0; j < n - 1; j++) {printf("%d ", schedule[i][j]);}printf("\n");}for (int i = 0; i < n; i++) {free(schedule[i]);}free(schedule);return 0;
}
代码解释:
这段代码与之前的实现基本相同,只是使用了动态内存分配来创建二维数组。在 main 函数中,我们先使用 malloc 分配一个 n 行的指针数组 schedule,并在 roundRobinSchedule 函数中也使用 malloc 分配了一个 n/2 行、(n/2-1) 列的二维数组 subSchedule。在完成循环赛日程表的构建后,我们需要记得先释放 subSchedule 申请的内存,再释放 schedule 申请的内存,以避免内存泄漏。
C++实现:
#include <iostream>
#include <vector>using namespace std;vector<vector<int>> roundRobinSchedule(int n) {if (n == 1) {vector<vector<int>> result(1, vector<int>(1, 0));return result;}vector<vector<int>> schedule(n, vector<int>(n - 1));vector<vector<int>> subSchedule = roundRobinSchedule(n / 2);for (int i = 0; i < n / 2; i++) {for (int j = 0; j < n - 1; j++) {int team1 = subSchedule[i][j % (n / 2)] + (j / (n / 2)) * (n / 2);int team2 = (n - 1) - subSchedule[i][j % (n / 2)] + (j / (n / 2)) * (n / 2);schedule[team1][i] = team2;schedule[team2][i] = team1;}}if (n % 2 == 1) {for (int i = 0; i < n - 1; i++) {schedule[n - 1][i] = i;schedule[i][n - 1] = n - 1 - i;}}return schedule;
}int main() {int n = 6;vector<vector<int>> schedule = roundRobinSchedule(n);for (int i = 0; i < n; i++) {for (int j = 0; j < n - 1; j++) {cout << schedule[i][j] << " ";}cout << endl;}return 0;
}
代码解释:
这段代码实现了循环赛日程表的构建。其中,roundRobinSchedule 函数使用分治算法,递归地构建出小规模的日程表,并将它们合并起来得到最终的日程表。在实现过程中,我们使用了二维向量 schedule 来存储日程表,其第一维表示参赛队伍,第二维表示比赛轮次。在每个轮次中,我们使用 subSchedule 子日程表来记录参赛队伍之间的比赛对阵情况。最终,我们将子日程表中的比赛结果放到总日程表中对应的位置上,得到完整的循环赛日程表。
在 main 函数中,我们调用 roundRobinSchedule 函数构建了一个大小为6的循环赛日程表,并将其打印输出。
更优化的算法:
好的,下面我会具体讲解一下循环移位矩阵法和压缩算法。
循环移位矩阵法
循环移位矩阵法是一种将循环赛日程表问题转化为矩阵问题的方法,它可以通过矩阵的循环移位来生成日程表。
具体实现步骤如下:
(1)构造一个大小为n x n的矩阵,初始值都为0;
(2)在矩阵的第一行第一列放置1;
(3)依次填充矩阵的其它位置,填充规则如下:
a. 如果当前位置在矩阵的第一行,那么下一个位置应该是矩阵的最后一列的下一行。
b. 如果当前位置在矩阵的最后一列的下一行,那么下一个位置应该是矩阵的第一行。
c. 如果当前位置不满足a和b两个条件,那么下一个位置应该是当前位置的右上方。
(4)根据矩阵的每一行来生成对应的日程表。
该算法的时间复杂度为O(n^2),与传统的循环赛日程表算法相同,但是可以减少循环的次数,从而提高算法的效率。
压缩算法
压缩算法是一种只生成需要的那一行或那一列的算法,避免浪费时间和空间。该算法的实现思路是,首先利用循环赛日程表算法生成完整的日程表,然后只保留需要的那一行或那一列。
具体实现步骤如下:
(1)根据循环赛日程表算法生成完整的日程表;
(2)如果需要生成第i行日程表,则只保留日程表中第i行的数据,其它行的数据全部删除;
(3)如果需要生成第i列日程表,则只保留日程表中第i列的数据,其它列的数据全部删除。
该算法的时间复杂度取决于循环赛日程表算法的时间复杂度,如果原始算法的时间复杂度为O(n^2),则压缩算法的时间复杂度也为O(n^2)。但是压缩算法可以减少内存的占用,避免浪费时间和空间。
总结
1.注意实现问题
(1)在使用分治策略解決问题时 ,注意检查四个条件是否满足
(2)尽量保证划分出的子问题规模大致一致。平衡子问题思想
(3)如果可以使用递推的方式解决问题,尽量使用递推算法
(4)递归的分治算法的时间复杂性分析,要先写出其时间复杂
性的递归方程,然后用主定理或递归树解方程。
(5)用递归算法解决问题时,要分析出其边界条件和递归方程(过程)
2.当用C语言和C++实现循环赛日程表算法时,需要注意以下几点:
- 在C语言中,需要手动进行内存管理,如使用malloc和free函数动态分配和释放内存,避免内存泄漏或访问非法内存。而在C++中,可以使用new和delete操作符,或使用智能指针等RAII技术来管理内存,使得代码更加安全和简洁。
- 在C语言中,数组下标从0开始,而在C++中,数组下标从1开始,因此在实现算法时需要注意数组的下标问题。
- 在C++中,可以使用STL容器如vector等来方便地管理数组,而在C语言中需要手动实现相关操作,如插入、删除和查找等。
- 在C++中,可以使用类和对象的概念来封装和组织代码,使得代码更加模块化和可复用。而在C语言中,可以使用函数和结构体等来实现类似的功能。
- 在实现算法时,需要考虑代码的可读性和可维护性,如合理命名变量和函数、添加注释、遵循编程规范等,从而使得代码更易于理解和修改。
3.这个算法和游戏的联系:
线性时间选择算法可以用来解决一些游戏中的问题。例如,有些游戏中需要计算排名,比如排行榜、竞技场排名等。在这些场景中,需要快速地找到某个玩家的排名,而线性时间选择算法可以用来解决这个问题。这怎么少得了王者农药呢?

具体来说,可以将玩家的战斗力作为数组的值,然后使用线性时间选择算法找到战斗力排名第k的玩家,这样就可以快速地计算出某个玩家在排名中的位置。
此外,线性时间选择算法还可以用来解决其他游戏中的问题,比如寻找最强的敌人、寻找最优的游戏策略等。

相关文章:

2.11 循环赛日程表
博主简介:一个爱打游戏的计算机专业学生博主主页: 夏驰和徐策所属专栏:算法设计与分析 目录 书本内容: 我的理解: 更优化的算法: 总结 1.注意实现问题 2.当用C语言和C实现循环赛日程表算法时ÿ…...

SpringBoot——SB整合mybatis案例(残缺版本)第三集
了解完使用阿里云存储的操作后,现在需要在案例里面集成阿里云进行开发。云服务——阿里云OSS的入门使用_北岭山脚鼠鼠的博客-CSDN博客 阿里云OSS——集成 对于前端传过来的图片要先上传到OSS,然后获取图片在云端的访问地址,存储到数据库里面…...
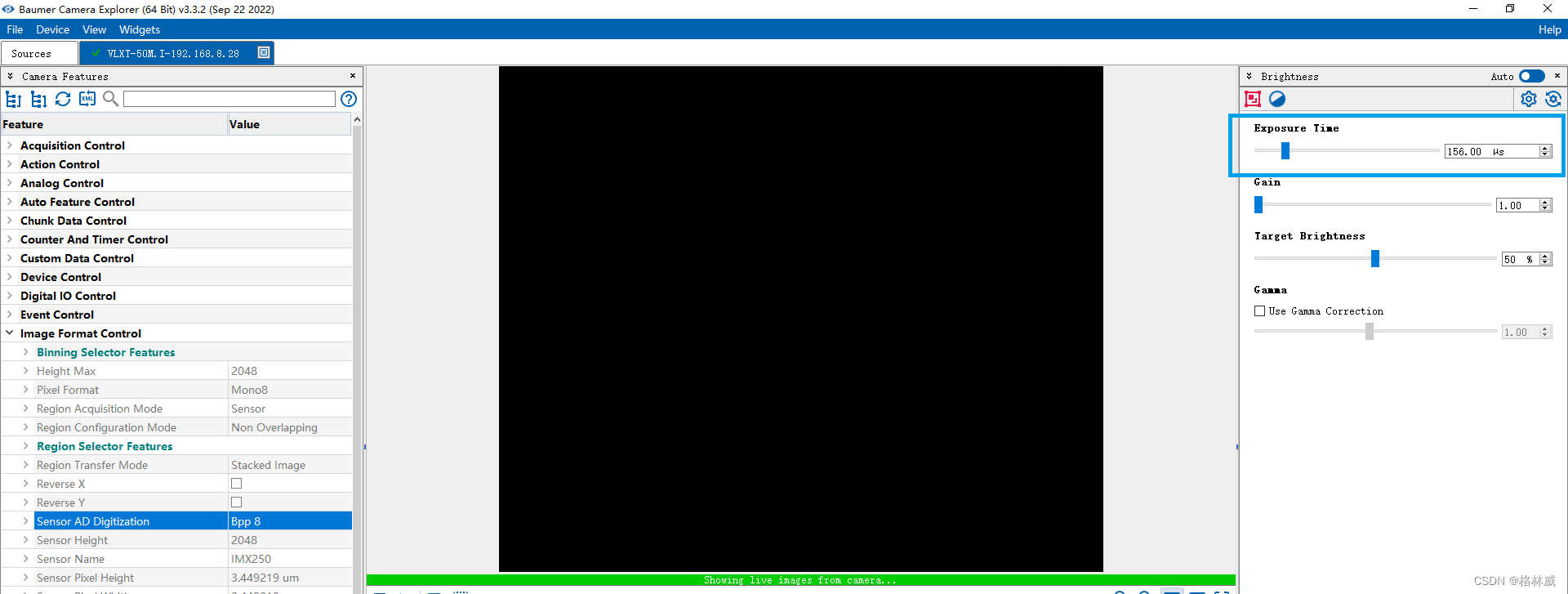
Baumer工业相机堡盟相机不满帧如何使用CameraExplorer设置相机参数让它的帧率达到满帧
项目场景 Baumer工业相机堡盟相机是一种高性能、高质量的工业相机,可用于各种应用场景,如物体检测、计数和识别、运动分析和图像处理。 Baumer的万兆网相机拥有出色的图像处理性能,可以实时传输高分辨率图像。此外,该相机还具…...

巴黎爱情回忆 NFT 作品集
由 Metaverse Studio 制作。 欢迎来到浪漫之都巴黎!尽情游览美丽壮观的地标,探索法国文化。在离开之前,别忘了从《巴黎爱情回忆》NFT 作品集中带走一件纪念品。从世界著名的法国人物到标志性资产,这些 NFT肯定会为您的钱包带来巴黎…...
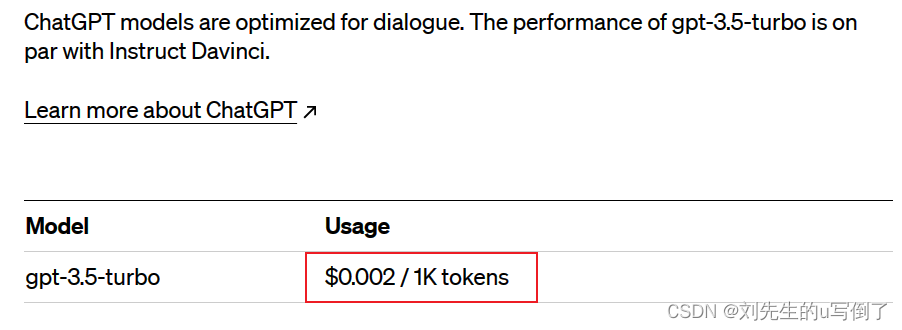
openai开放gpt3.5-turbo模型api,使用python即可写一个基于gpt的智能问答机器人
1安装python库 使用pip安装openai库,注意gpt3.5-turbo模型需要python>3.9的版本支持,本文演示的python版本是python3.10.10 pip install openai2创建api key 需要提前在openai官网上注册好账号,然后打开https://platform.openai.com/ac…...
GUI开发--LCD屏幕的使用(非第三方库)--笔记
导:界面交互需要GUI,GUI需要文字和图片,所有此处总结在M4芯片上实现GUI的基本操作!该芯片具有160K大小的内存,有512K的flash;故而没有使用第三方库! LCD屏幕的使用--笔记 1.汉字显示-两种方式…...

CesiumForUnreal实现地形等高线效果
文章目录 1.实现目标2.实现过程2.1 实现原理2.2 具体过程3.参考资料1.实现目标 在UE5中使用CesiumForUnreal插件添加Cesium World Terrain在线的世界地形,然后以25米为等高距,绘制一定范围内的等高线,如下图所示: 2.实现过程 由于这里直接使用CesiumForUnreal插件加载的在…...

Python爬虫——Python Selenium基本用法
Selenium 作为一款 Web 自动化测试框架,提供了诸多操作浏览器的方法,这里对其中的常用方法做详细介绍。 定位节点 Selenium 提供了 8 种定位单个节点的方法,如下所示: 定位节点方法方法说明find_element_by_id()通过 id 属性值定…...
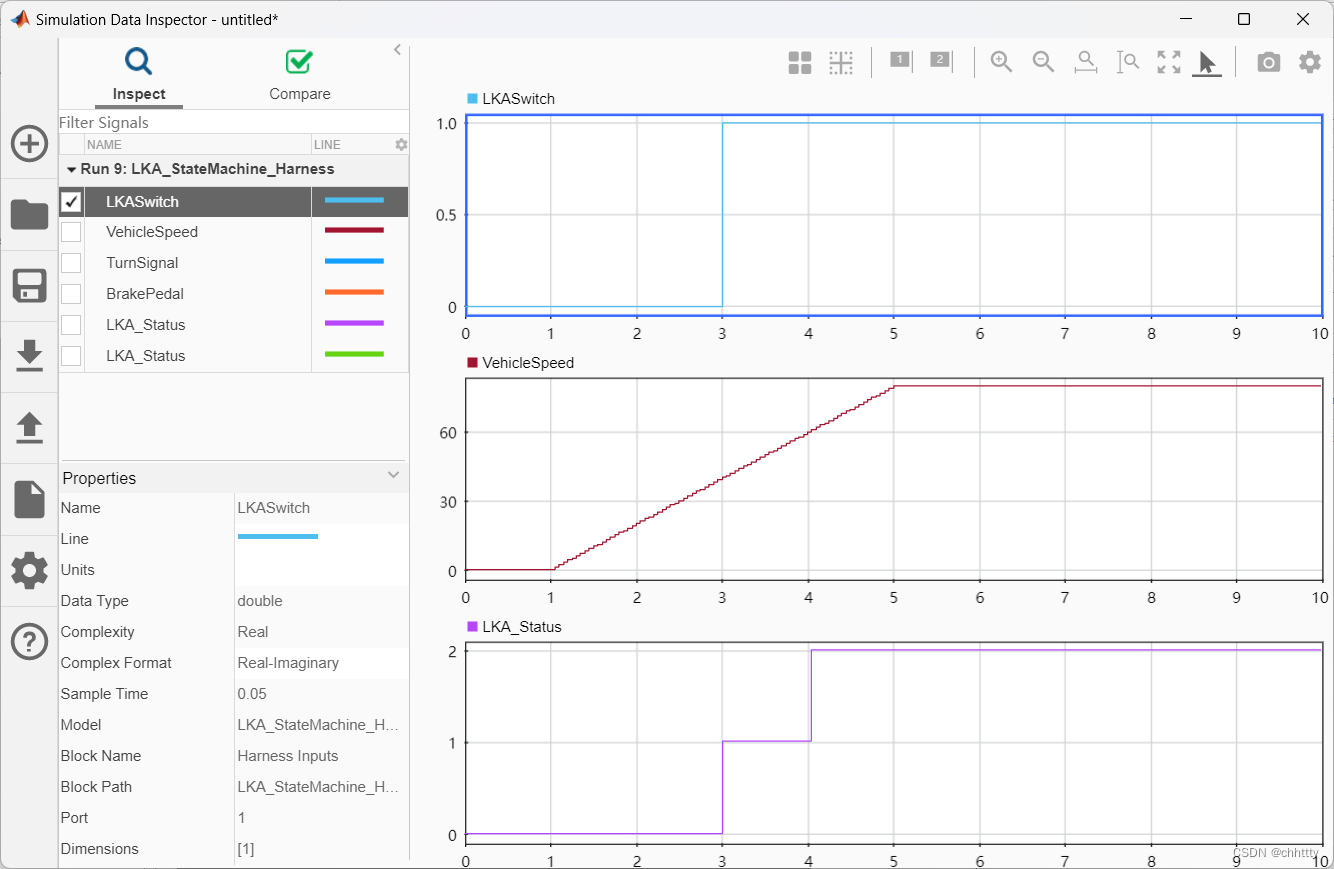
仿真与测试:单元测试与Test Harness
本文描述单元测试的概念,以及Test Harness建立的方法和简单的单元测试过程。 文章目录1 单元测试1.1 场景举例1.2 简单的测试方法2 Test Harness建立2.1 模型配置2.2 创建Test Harness3 总结1 单元测试 单元测试,简单来说就是在Simulink模型中只测试一小…...

面试常问集锦——MySQL部分
Mysql速成大法 请签收MySQL灵魂十连 https://mp.weixin.qq.com/s?__bizMzI4NjI1OTI4Nw&mid2247488721&idx1&sneead82d2b7a0fdf993beacc4dfd60313&chksmebdef5e9dca97cff9d638877e5855850727ae26ebcfd60c7700ae53e311fa6ddb64b63bb9552&scene178&cur_a…...

算法训练第四十四天|完全背包理论 、518. 零钱兑换 II、377. 组合总和 Ⅳ
第九章 动态规划part06完全背包理论基础完全背包C测试代码总结518. 零钱兑换 II题目描述思路总结377. 组合总和 Ⅳ题目描述思路总结完全背包理论基础 参考:https://programmercarl.com/%E8%83%8C%E5%8C%85%E9%97%AE%E9%A2%98%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80%…...
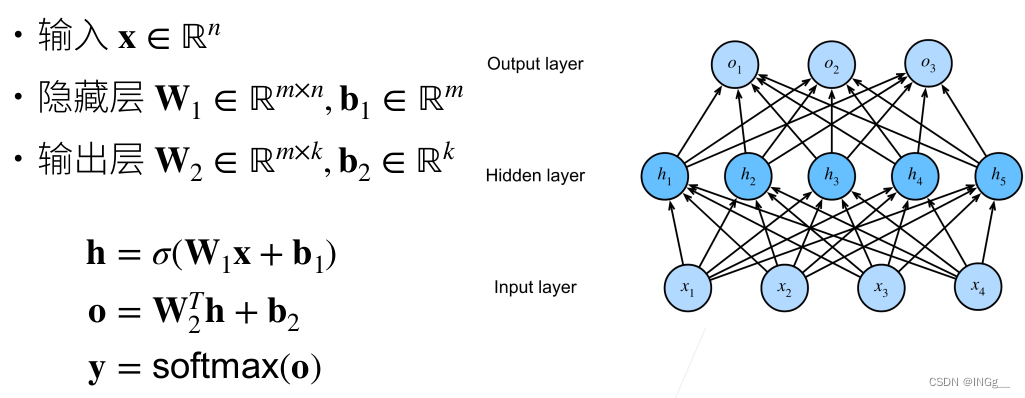
0x06多层感知机
感知机 感知机形象的来看就是我们接触过的一个只有两个部分组成(输出和输入)组成的最简单的神经网络之一。 给定输入x,权重w和偏移b以及一个感知函数,感知机就能输出: 这个函数可以形象的用作二分类问题,…...
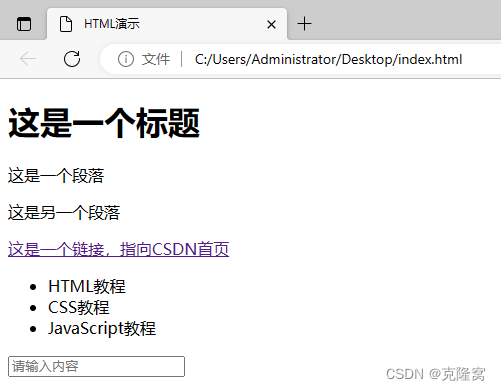
HTML是什么?HTML简介
HTML 英文全称是 Hyper Text Markup Language,中文译为“超文本标记语言”,专门用来设计和编辑网页。 使用 HTML 编写的文件称为“HTML 文档”,一般后缀为.html(也可以使用.htm,不过比较少见)。HTML 文档是…...

Linux定时服务
目录 1、定时器操作 2.cron表达式的语法规则 参考链接 1、定时器操作 sudo crontab -e 【选择2】 进入进行配置【需要按下 i 】 #sh /home/xx/crontabsh/test.sh的意思是,让sh解释器调用test.sh脚本,到达定时执行任务的效果 # 每一分钟执行一次 *…...

sgi_stl源码学习,官方文档3.2.3String package字符串封装,未完待续
https://www.boost.org/sgi/stl/character_traits.html char_traits<char> char_traits<wchar_t>traits翻译为特征、特性类,一般是指某种类型的特性类应该提供的一组接口、类型定义。 web页面描述了一些接口要求。感觉没有什么特别的。直接看代码吧 c…...
:基础知识)
从JavaScript到Java(一):基础知识
Hello World Java和JavaScript虽然有不同的特点,但在一些概念和知识点上是相似的。本文从JavaScript开发者的角度出发,帮助你理解Java基础知识(反过来也行)。 // 解释型 console.log("Hello, World!");// 编译型 pub…...

Android编舞者类Choreographer小结
Android编舞者类Choreographer小结 作用 编舞者类的作用主要是控制绘制节奏,用于发起一次vsync垂直同步信号的监听,当垂直同步信号来的时候会回调注册的Runnable或者FramCallback Choreographer对象获取 Choreographer对象是通过它的getInstance方法…...

大专升本科难度大吗 需要考哪些科目
大专学历可以通过自考和成考提升学历到本科,自考的考试科目有12-16门左右,考试内容不难,但是考试周期长,需要考生通过所有课程才能申请毕业。成考专升本考试科目有政治,外语和专业课,考试内容简单ÿ…...

考研复试-英语问答+解答
每个问题2~3min 一、 1.考官问问题,没听明白 I’m sorry, I didn’t hear that clearly. May I ask you to repeat it, please? Sorry, I have no clear idea about this question for now, but I will think about it later. And if possible, I want to discuss …...
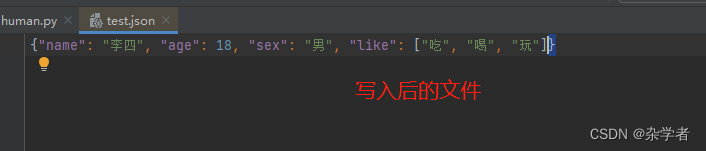
python 文件相关的操作 常用函数(读文件、写文件、文件的追加内容、修改文件内容、复制文件、按行读取文件、with open) json文件的读取
常用函数:open(打开文件),read(读文件到程序中),write(写程序中的变量到文件),close(关闭文件) 示例1:读文件(…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

Qwen3-Embedding-0.6B深度解析:多语言语义检索的轻量级利器
第一章 引言:语义表示的新时代挑战与Qwen3的破局之路 1.1 文本嵌入的核心价值与技术演进 在人工智能领域,文本嵌入技术如同连接自然语言与机器理解的“神经突触”——它将人类语言转化为计算机可计算的语义向量,支撑着搜索引擎、推荐系统、…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...
