数据结构:树、森林
二叉树与树结构差异
-
树(一般树):树是一种数据结构,其中每个节点可以有任意数量的子节点(除了根节点和叶子节点外)。因此,一般树的节点在数组中的表示并不是那么直接,特别是当树不是完全二叉树时。
-
二叉树:二叉树是一种特殊的树,其中每个节点最多有两个子节点(通常称为左子节点和右子节点)。这种结构使得二叉树在数组中的表示更加直接和高效,特别是当二叉树是完全二叉树或满二叉树时。
顺序存储的差异:
-
一般树的顺序存储:对于一般树,由于其子节点的数量不固定,因此很难在数组中直接表示。如果尝试使用顺序存储,可能会导致大量的空间浪费,因为需要为不存在的子节点预留空间。此外,访问子节点和父节点的索引计算也会变得复杂,因为需要额外的数据结构(如指针或索引数组)来跟踪每个节点的子节点位置。
-
二叉树的顺序存储:对于二叉树,特别是完全二叉树或满二叉树,顺序存储非常高效。每个节点都可以根据其在数组中的索引来直接访问其左子节点和右子节点(通过简单的数学计算)。同样,也可以通过索引计算来找到父节点。这种存储方式不仅节省了空间(因为没有为不存在的子节点预留空间),而且访问速度也很快。
总的来说就是树的顺序存储结构中,数组下标代表结点的编号,下标所存的内容指示了节点之间的关系,而二叉树的数组下标即表示结点的编号又指示了二叉树中各结点之间的关系。
应用场景:
-
一般树的顺序存储:由于上述的空间浪费和访问复杂性,一般树的顺序存储并不常见。相反,它们更常使用链式存储(如通过指针连接节点),这样可以更灵活地表示任意数量的子节点。
-
二叉树的顺序存储:二叉树的顺序存储特别适用于完全二叉树或满二叉树,以及那些可以通过某种方式(如旋转或修改)转化为这些特殊类型的二叉树。此外,顺序存储的二叉树在某些特定应用中(如堆排序中的堆结构)也非常有用。
结论:
二叉树和树的顺序存储结构在本质上是相似的,但由于二叉树结构的特殊性,它在顺序存储中更加高效和直接。对于一般树,顺序存储通常不是最佳选择,而链式存储则更为常见和实用。
树和二叉树是两种常见的树形数据结构,它们之间可以相互转换。这种转换在处理树形结构的问题时非常有用,因为二叉树具有一些特殊的性质(如左子树和右子树的明确区分)和高效的算法(如二叉搜索树、堆等)。以下是树和二叉树相互转换的详细过程:
树转换为二叉树
树转换为二叉树的过程通常基于“儿子兄弟表示法”。在这种表示法中,每个节点都有指向其第一个孩子和下一个兄弟节点的指针。在转换为二叉树时,我们可以将节点的第一个孩子视为二叉树的左孩子,将节点的下一个兄弟视为二叉树的右孩子。具体步骤如下:
-
添加虚根(可选):如果原树是一个森林(即多棵树),则首先添加一个虚根节点,将森林中的所有树作为这个虚根的子树。这一步是可选的,因为对于单棵树来说,不需要添加虚根。
-
转换过程:
- 对于树中的每个节点,将其第一个孩子节点作为二叉树的左孩子。
- 将该节点的下一个兄弟节点(即与其共享同一父节点的下一个节点)作为二叉树的右孩子。
- 递归地对每个子树执行上述操作。
-
去除虚根(如果添加了):在转换完成后,如果添加了虚根,则将其去除,得到最终的二叉树。

二叉树转换为树
二叉树转换为树的过程是上述转换的逆过程。具体步骤如下:
- 恢复兄弟关系:
- 从二叉树的根节点开始,遍历整棵树。
- 对于每个节点,如果它存在右孩子,则将该右孩子视为原树中其左孩子的下一个兄弟节点。
- 注意,在二叉树中,一个节点的左孩子和右孩子分别对应原树中的第一个孩子和下一个兄弟节点。
- 递归处理:
- 对二叉树的每个子树递归执行上述操作,以恢复整棵树的兄弟关系。
- 结果:最终得到的是一棵或多棵树的集合(如果原二叉树是由多个树的根节点组成的森林转换而来)。

注意事项
- 在转换过程中,需要确保不会破坏原树或二叉树的结构。
- 转换后的树或二叉树应保留原树的所有节点和边。
- 如果原树是森林,则在转换为二叉树时需要添加虚根;在转换回树时,如果添加了虚根,则需要将其去除。
通过上述过程,我们可以实现树和二叉树之间的相互转换,从而在处理树形结构的问题时更加灵活和高效。
树的遍历
先根遍历:
- 先访问根节点
- 再依次访问根结点的每棵子树
- 与该树对应的二叉树的先序序列相同
后根遍历:
- 先依次遍历根结点的每棵子树,遍历子树时仍遵循先子树后根的原则
- 再访问根结点
- 与该树对应的二叉树的中序序列相同
森林的遍历
先序遍历森林:
- 对森林中的树一次采用先序遍历
中序遍历森林:
- 对森林中的树依次采用后根遍历
树与二叉树的应用:
哈夫曼树(Huffman Tree)
又称最优二叉树,是一种具有特殊性质的二叉树结构。其定义及相关术语如下:
定义
给定N个权值作为N个叶子结点,构造一棵二叉树,若该树的带权路径长度达到最小,则称这样的二叉树为最优二叉树,也称为哈夫曼树。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
相关术语
-
结点的权:在哈夫曼树中,每个结点都被赋予一个具有某种现实含义的数值,这个数值被称为该结点的权。权值可以表示结点的重要性、频率或其他任何需要优化的指标。
-
路径和路径长度:
- 路径:在一棵树中,从一个结点往下可以达到的孩子或孙子结点之间的通路称为路径。
- 路径长度:在一条路径中,每经过一个结点,路径长度增加1。若根结点所在层数为1,则从根结点到第L层结点的路径长度为L-1。
-
结点的带权路径长度(WPL):从根结点到该结点之间的路径长度与该结点的权的乘积。这个值反映了结点在整个树中的重要性与其位置的关系。
-
树的带权路径长度(WPL):树中所有叶结点的带权路径长度之和。对于哈夫曼树而言,其WPL是所有可能的二叉树中最小的。
-
构造哈夫曼树:
- 初始时,将给定的N个权值分别作为N棵仅含一个结点的二叉树的根结点,构成森林。
- 重复执行以下步骤,直到森林中只剩下一棵树为止:
- 从森林中选出两棵根结点权值最小的树,将它们合并为一棵新的二叉树,新结点的权值为这两棵树根结点的权值之和。
- 将新得到的树加入森林中,并删除原来的两棵树。
3. 最终得到的树即为哈夫曼树
哈夫曼树的性质:
- 每个初始结点最终都成为叶结点,且权值越小的结点到根结点的路径长度越大。
- 哈夫曼树的结点总数为2N-1,其中N为初始结点数(也即叶结点数)。
- 哈夫曼树中不存在度为1的结点(即每个非叶结点都有两个子结点)。
- 哈夫曼树并不唯一,但所有可能的哈夫曼树的WPL必然相同且为最优。

哈夫曼编码:
基于哈夫曼树的一种数据压缩方法。通过对数据中的字符进行频率统计,构建哈夫曼树,并根据树的结构为字符分配不同的编码(通常是二进制编码),从而实现数据的压缩。哈夫曼编码有静态和动态两种形式,分别适用于不同的应用场景。
哈夫曼编码和定长编码:
哈夫曼编码是一种非常有效的数据压缩编码。由哈夫曼树得到哈夫曼编码是很自然的过程。首先,将每个字符当作一个独立的结点,其权值为它出现的频度(或次数),构造出对应的哈夫曼树。然后,将从根到叶结点的路径上分支标记的字符事作为该字符的编码。

这棵哈夫曼树的 WPL 为
WPL =1x45+3x(13+12+16)+4x(5+9)=224
此处的 WPL 可视为最终编码得到二进制编码的长度,共224位。若采用3位固定长度编码,则得到的二进制编码长度为300位,因此哈夫曼编码共压缩了25%的数据。利用哈夫曼树可以设计出总长度最短的二进制前缀编码。
总结:
哈夫曼树在数据压缩、信息论等领域有着广泛的应用。通过构建哈夫曼树,可以实现数据的高效压缩和解压缩,从而减少存储空间和传输时间。
相关文章:

数据结构:树、森林
二叉树与树结构差异 树(一般树):树是一种数据结构,其中每个节点可以有任意数量的子节点(除了根节点和叶子节点外)。因此,一般树的节点在数组中的表示并不是那么直接,特别是当树不是完…...

AI Agent应用出路到底在哪?
1 Agent/Function Call 的定义 Overview of a LLM-powered autonomous agent system: Agent学会调用外部应用程序接口,以获取模型权重中缺失的额外信息(预训练后通常难以更改),包括当前信息、代码执行能力、专有信息源…...

一文了解构建工具——Maven与Gradle的区别
目录 一、Maven和Gradle是什么? 构建工具介绍 Maven介绍 Gradle介绍 二、使用时的区别: 1、新建项目 Maven: Gradle: 2、配置项目 Maven: Gradle: 3、构建项目——生成项目的jar包 Gradle&…...

electron介绍
Electron中文文档 Electron是什么? Electron是一个使用 JavaScript、HTML 和 CSS 构建桌面应用程序的框架。 Electron 允许开发者使用前端技术栈来创建可以在 Windows、macOS 和 Linux 等多个操作系统上运行的桌面应用程序。 Electron 本质上是一个运行在桌面操作…...

Redis-持久化
首先,我们明白一个概念, 硬盘>持久 内存>不持久 而Redis是一个内存数据库,不持久,相比于Mysql这样的关系型数据库,最明显的特点是快/效率高 为了保证速度快,数据要保存再内存中,为了持久,存储在硬盘上 所以redis决定: 插入>内存+硬盘(硬盘是为了在re…...
)
封装轮播图 (因为基于微博小程序,语法可能有些出入,如需使用需改标签)
这是在组件中使用,基于微博语法 <template><wbx-view class"" style"width: 100vw;height: 70vh;"><WBXswiper change"gaibian" :vertical"false" :current"current" indicatorActiveColor"…...

【Ubuntu】minicom安装、配置、使用以及退出
目录 1 安装 2 配置 3 使用 4 退出 minicom是一个串口通信的工具,以root权限登录系统,可用来与串口设备通信。 1 安装 sudo apt-get install minicom 2 配置 使用如下命令进入配置界面: sudo minicon -s 进入配置界面后,…...

MYSQL的监控
1. MySQL服务器都提供了哪几种类型的日志文件?说明每种日志的用途。 Error log:启动、关闭和异常有关的诊断信息 General query log:服务器从客户端收到的所有语句 Slow query log:需要很长时间执行的查询 Audit log:企业版基于策略的审计 Binary…...

CTF ciscn_2019_web_northern_china_day1_web2
ciscn_2019_web_northern_china_day1_web2 BEGIN 拿到题目,先看看 这里发现一个很像提示的东西,然后发现下面是一堆小电视商品,有lv等级和金钱,所以这题的入口可能就是再lv6和这个资金募集上 然后点击下next,看看页…...

linux中vim编辑器的应用实例
前言 Linux有大量的配置文件,其中编辑一些配置文件,最常用的工具就是 Vim ,本文介绍一个实际应用的Vim编辑器开发文档的实例。 Vim是一个类似于Vi的著名的功能强大、高度可定制的文本编辑器,在Vi的基础上改进和增加了很多特性。…...

智慧城市交通管理中的云端多车调度与控制
城市交通管理中的云端多车调度与控制 智慧城市是 21世纪的城市基本发展方向,为了实现智慧城市建设的目标,人们需要用现代化的手段去管理和控制城市中的各种资源和设施。智能交通控制与管理是智慧城市中不可缺少的一部分,因为现代城市交通系统…...

分治(归并排序)
一、基本思路 我们以一个归并排序为例。 . - 力扣(LeetCode) 归并排序的思想:得到两个有序数组,把两个有序数组合并,传到下一层递归,一直得到两个有序数组,一直合并,最后就能得到有…...

小学生为什么要学英语
小学生需要学习英语的原因有很多,以下是其中的一些原因(毕竟我也会累滴(* ̄▽ ̄*)): 1. 全球化交流:英语是国际交流的通用语言,学习英语可以帮助小学生更好地融入全球化的社会环境&am…...

企业云存储如何收费?企业云存储收费标准
企业云存储如何收费?企业云存储的收费方式因不同的服务提供商和具体的服务选项而异,通常从用户数量、存储容量、功能、混合收费、按需定价、定制化、功能模块等多个方面进行考量。以下是对其多方面收费方式的详细介绍: 1.按用户数量收费 适用…...

一步步教你LangGraph Studio:可视化调试基于LangGraph构建的AI智能体
之前我们在第一时间介绍过使用LangChain的LangGraph开发复杂的RAG或者Agent应用,随着版本的迭代,LangGraph已经成为可以独立于LangChain核心,用于开发多步骤、面向复杂任务、支持循环的AI智能体的强大框架。 近期LangGraph推出了一个使得复杂…...

用SpringBoot打造先进的学科竞赛管理系统
1绪 论 1.1研究背景 当今时代是飞速发展的信息时代。在各行各业中离不开信息处理,这正是计算机被广泛应用于信息管理系统的环境。计算机的最大好处在于利用它能够进行信息管理。使用计算机进行信息控制,不仅提高了工作效率,而且大大的提高了其…...

Linux入门攻坚——34、nsswitch、pam、rsyslog和loganalyzer前端展示工具
nsswitch:network service switch 名称解析:name <---> id 认证服务:用户名、密码验证或token验证等 名称解析和认证服务都涉及查找位置,即保存在哪里。如linux认证,passwd、shadow,是在文件中&…...
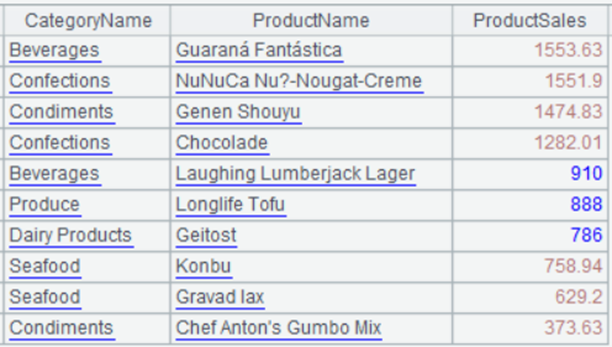
如何在Excel中快速找出前 N 名,后 N 名
有如下销售额统计表: 找出销售额排前 10 名的产品及其销售额,和销售额排倒数 10 名以内的产品及其销售额,结果如下所示: 前 10 名: spl("E(?1).sort(ProductSales:-1).to(10)",A1:C78)后 10 名࿱…...

创意实现!在uni-app小程序商品详情页轮播中嵌入视频播放功能
背景介绍 通过uni-app框架实现商城小程序商品详情页的视频与图片轮播功能,以提升用户体验和增加商品吸引力。通过展示商品视频和图片,用户可以更全面地了解商品细节,从而提高购买决策的便利性和满意度。这种功能适用于各类商品,如…...
WAF,全称Web Application Firewall,好用WAF推荐
WAF,全称Web Application Firewall,即Web应用防火墙,是一种网络安全设备,旨在保护Web应用程序免受各种Web攻击,如SQL注入、跨站脚本(XSS)、跨站请求伪造(CSRF)等。 WAF通…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility
Cilium动手实验室: 精通之旅---20.Isovalent Enterprise for Cilium: Zero Trust Visibility 1. 实验室环境1.1 实验室环境1.2 小测试 2. The Endor System2.1 部署应用2.2 检查现有策略 3. Cilium 策略实体3.1 创建 allow-all 网络策略3.2 在 Hubble CLI 中验证网络策略源3.3 …...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...
