我给Chat GPT写了个记忆系统
ChatGPT-LifeTime
OpenAI 的模型有一个固定的 Token 限制,例如 GPT-3 的 Davinci 模型最多可以处理2049 个 Token,大约 1500 个英文单词。最新 Turbo 模型大约是 4,096 个 Token,大约是 3000 个英文单词,也就是意味着Chat GPT它会”失忆“,但是它啥时候”失忆“呢?于是我写了个插件告诉我们,Chat GPT”失忆“了
AI has life too, that’s their memory
一些科普
ChatGPT自我阐述:
我是一个基于GPT-3的AI模型,用于自然语言处理和生成任务。在训练过程中,我使用了大量的文本数据,从中学习了语言规则、语法结构、上下文理解等方面的知识,并生成了模型参数和权重。这些参数和权重存储在我的内存中,使我能够在输入文本时生成相应的输出。
当我接收到一个输入时,我会将其转化为令牌序列,然后将其输入到模型中进行处理。在进行处理时,我会考虑输入的上下文、语法结构、语言规则等因素,并生成相应的输出。生成的输出也是一个令牌序列,可以通过后处理(例如去掉多余的标点符号和空格)进行最终的格式化。
然而,由于计算资源和性能的限制,模型的输入长度有所限制。目前最大的 GPT-3 模型(175B版本)的最大输入长度为2048个令牌(tokens),因此如果输入的文本长度超过了这个限制,模型可能会丢失先前的一些聊天记录。这并不是模型本身有意遗忘聊天记录,而是由于模型的输入和计算能力有限。如果您希望我更好地考虑您之前的聊天内容,您可以尝试将聊天内容分成更小的部分,或提供更具体的上下文信息。
- Token:这个指的是 OpenAI 处理文本的基本单位,可以是单词或者字符的片段。例如,“hamburger” 被分成 “ham”、“bur” 和 “ger” 三个 Token,而 “pear” 是一个 Token。1个 Token 大约相当于 4 个字符或者 0.75 个英文单词。
- 一些限制:
- OpenAI 的模型有一个固定的 Token 限制,例如 GPT-3 的 Davinci 模型最多可以处理2049 个 Token,大约 1500 个英文单词。最新 Turbo 模型大约是 4,096 个 Token,大约是 3000 个英文单词。
- 另外这个限制还有一个细节,Token 限制的计数包含输入和输出的文本。换句话说,不是说我输入 3000 个英文单词,然后 OpenAI 能返回 3000 个英文单词的结果,而是输入+输出总共不能超过 3000 个英文单词。
- 文字限制。目前 OpenAI 的 GPT-3 模型只能处理文字。
火爆的Character.AI也是如此,Character.AI 的角色倾向说的太多,而且会随着彼此的聊天内容增加,变得越来越像机器人。这时候需要用户将之前的聊天删除或存档,开始新的对话,但这就使得 Character “忘记”之前的聊天内容。
Character.AI:个性化的ChatGPT,AI大模型时代的UGC平台 | 人人都是产品经理
所以对于AI来说,也许它的生命就是它的记忆
The life of an ai is its memory
既然现在我们无法控制它们的”离去“,那是否可以让我看到它是否即将”老去“,好让我做个告别,起码不留遗憾
Cherish it today because it will be lost tomorrow
于是我编写了个谷歌插件,以便让我知晓,它即将”离我而去“

相关文章:

我给Chat GPT写了个记忆系统
ChatGPT-LifeTime OpenAI 的模型有一个固定的 Token 限制,例如 GPT-3 的 Davinci 模型最多可以处理2049 个 Token,大约 1500 个英文单词。最新 Turbo 模型大约是 4,096 个 Token,大约是 3000 个英文单词,也就是意味着Chat GPT它会…...

哈希表题目:砖墙
文章目录题目标题和出处难度题目描述要求示例数据范围解法思路和算法代码复杂度分析题目 标题和出处 标题:砖墙 出处:554. 砖墙 难度 5 级 题目描述 要求 你的面前有一堵矩形的、由 n\texttt{n}n 行砖块组成的砖墙。这些砖块高度相同(…...
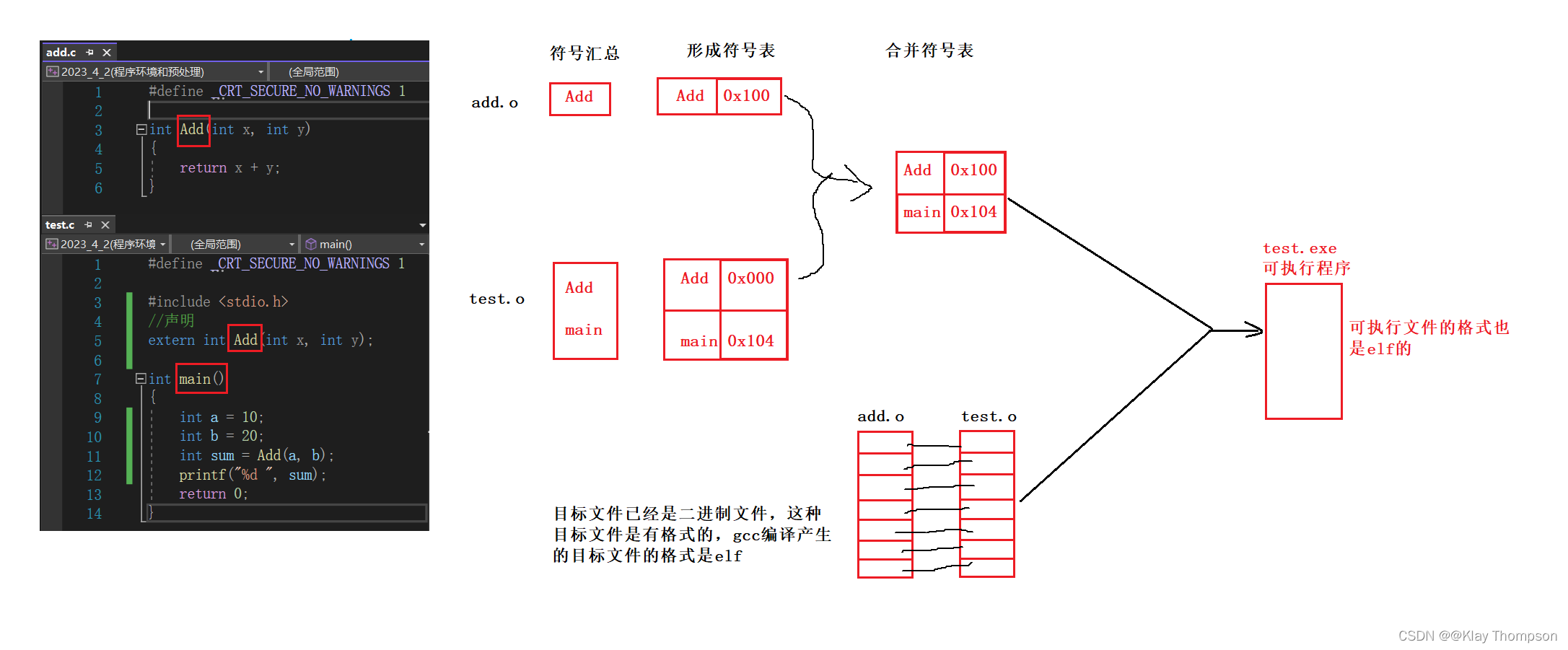
【程序环境详解】
每个源程序(.c文件)都需要经过编译链接形成 .exe的可执行文件。 在ANSI C的任何一种实现中,存在两个不同的环境 第一种是翻译环境,在这个环境中源代码被转换为可执行的机器指令。第二种是执行环境,它用于实际执行代码…...
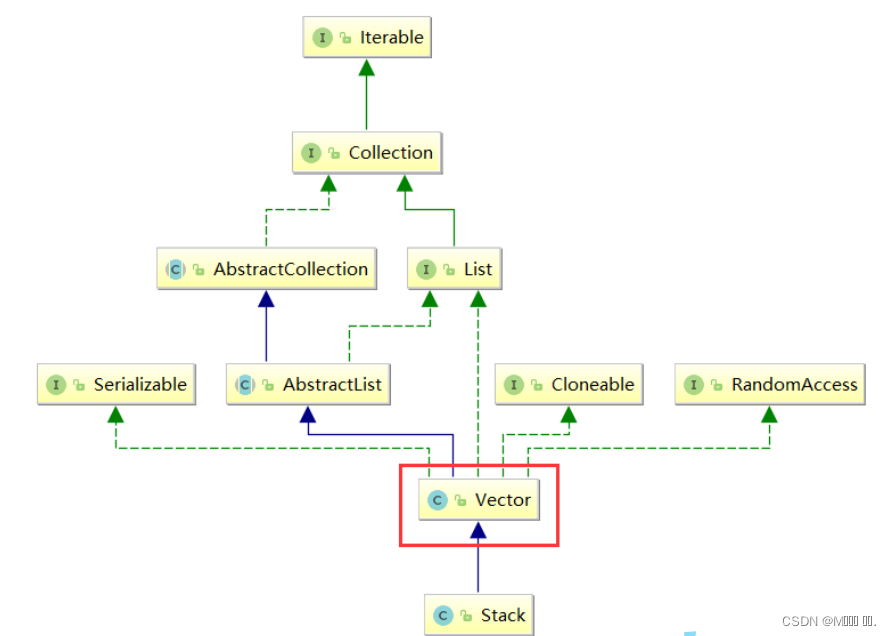
栈(Stack)
目录 1.1 概念 1.2 栈的使用 1.3 栈的模拟实现 1.4 栈的应用场景 1. 改变元素的序列 2. 将递归转化为循环 1.1 概念 栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶,另一端称为…...
【计算机网络】2、网络编程模型理论
文章目录一、网络基本概念1.1 网段1.2 子网掩码 netmask1.3 子网 subnet1.4 网络地址 network1.5 实战 192.168.0.1/27 的含义二、socket2.1 sockaddr 格式2.1.1 IPv4 sockaddr 格式2.1.2 IPv6 sockaddr 格式2.1.3 本地 sockaddr 格式2.2 http 与 websocket三、TCP 编程3.1 ser…...

jmeter接口测试及详细步骤以及项目实战教程
如果看完这篇文章还是不太明白的话,可以看看下面这个视频 2023年B站最新Jmeter接口测试实战教程,精通接口自动化测试只需要这一套视频_哔哩哔哩_bilibili2023年B站最新Jmeter接口测试实战教程,精通接口自动化测试只需要这一套视频共计16条视…...

抖音进攻,B站退守
“爱优腾芒”等长视频平台的崛起,在一定层面上丰富了人们的日常生活,而抖音、快手等短视频平台的出现,则在很大程度上改变了用户观看视频的方式。只不过,近几年,随着流量增长逐渐遭遇瓶颈,各视频平台便纷纷…...
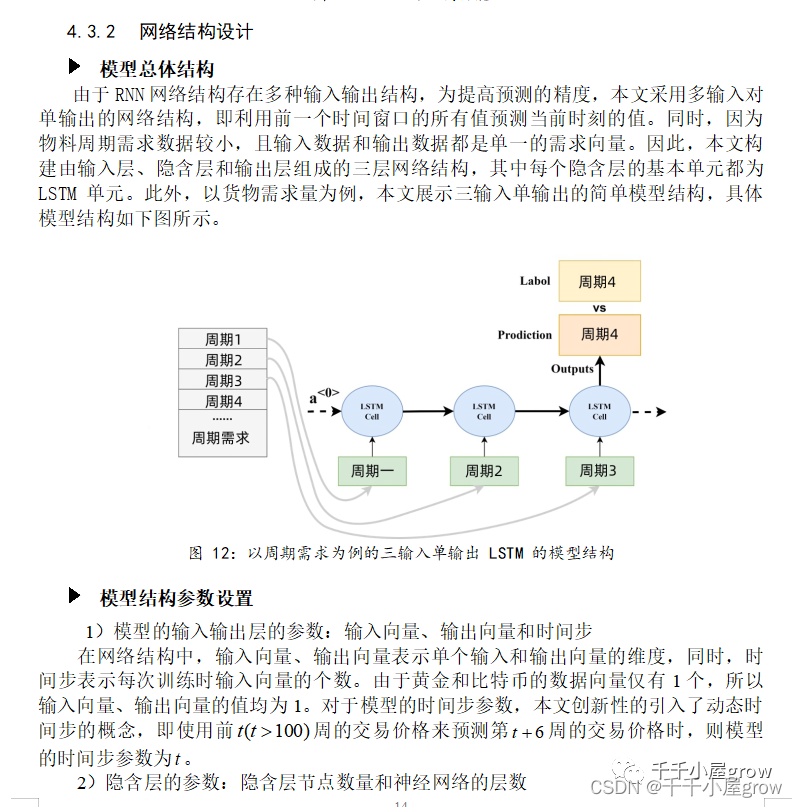
2022国赛E题完整成品文章数据代码模型--小批量物料的生产安排
基于LSTM循环神经网络的小批量物料生产安排分析 摘要 某电子产品制造企业面临以下问题:在多品种小批量的物料生产中,事先无法知道物料的 实际需求量。企业希望运用数学方法,分析已有的历史数据,建立数学模型,帮助企业…...
学生党,快来 Azure 一起学习 OpenAI (一):注册 Azure 和申请 OpenAI
大家好我是微软学生大使 Jambo , 在刚结束的微软学生开发者峰会 2023中我们了解到微软为学生提供了 Azure for Student 大礼包,通过 Azure for Student 除了学习和部署云原生的应用外,还可以申请使用 Microsoft OpenAI Service 。在这个 AIGC 火热的年代…...
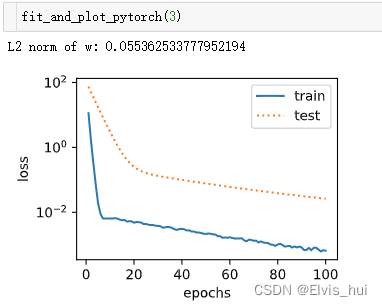
深入理解【正则化的L1-lasso回归和L2-岭回归】以及相关代码复现
正则化--L1-lasso回归和L2-岭回归1- 过拟合 欠拟合 模型选择2- 正则L1与L23- L2正则代码复现3-1 底层逻辑实现3-2 简洁实现1- 过拟合 欠拟合 模型选择 1-1 欠拟合: 在训练集和测试集上都不能很好的拟合数据【模型过于简单】 原因: 学习到的数据特征过少 …...
入侵检测——如何实现反弹shell检测?
反弹shell的本质:就是控制端监听在某TCP/UDP端口,被控端发起请求到该端口,并将其命令行的输入输出转到控制端。reverse shell与telnet,ssh等标准shell对应,本质上是网络概念的客户端与服务端的角色反转。 反弹shell的结…...
Python常用语句学习
人生苦短,我用Python。 ——吉多范罗苏姆 文章目录前言一、判断语句(一)if语句1. 作用2. 构成3. 语法4. 样例5.说明(二)if嵌套二、循环语句(一)while循环1. 作用2. 语法3. 样例4. 说明ÿ…...
测试3年还不如应届生,领导一句点醒:“公司不是只雇你来点点点的”
你的身边,是否有这样的景象? A:写了几年代码,写不下去了,听说测试很好上手,先来做几年测试 。 B:小文员一枚,想入行 IT,听说测试入门简单,请问怎么入行 。 …...

华为网络设备之路由策略,前缀列表(使用,规则)
华为网络之路由策略 前言:在企业网络的设备通信中,常面临一些非法流量访问的安全性及流量路径不优等问题,故为保证数据访问的安全性、提高链路带宽利用率,就需要对网络中的流量行为进行控制,如控制网络流量可达性、调…...

白噪音简介与实现
一、简介: 白噪音(White Noise)是一种具有平均功率频谱密度的噪音信号,其功率在所有频率上均匀分布。白噪音是一种随机信号,其包含所有频率成分的等幅随机振荡。因此,白噪音看起来像是一种随机的“嘈杂声”…...

Springboot结合线程池的使用
1.使用配置文件配置线程的参数 配置文件 thread-pool:core-size: 100max-size: 100keep-alive-seconds: 60queue-capacity: 1配置类 Component ConfigurationProperties("thread-pool") Data public class ThreadPoolConfig {private int coreSize;private int ma…...

AOP工作流程
AOP工作流程3,AOP工作流程3.1 AOP工作流程流程1:Spring容器启动流程2:读取所有切面配置中的切入点流程3:初始化bean流程4:获取bean执行方法验证容器中是否为代理对象验证思路步骤1:修改App类,获取类的类型步骤2:修改MyAdvice类,不增强步骤3:运行程序步骤…...
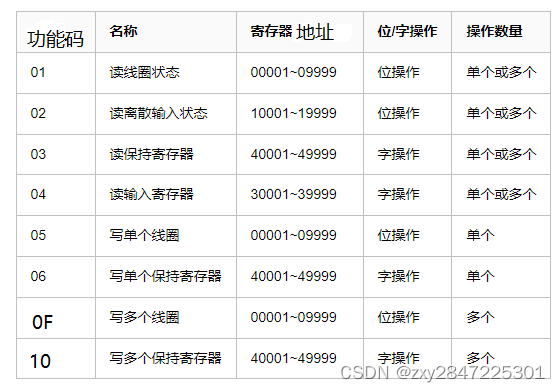
Modbus相关知识点及问题总结
本人水平有限,写得不对的地方望指正 困惑:线圈状态的值是否是存储在线圈寄存器里面?是否有线圈寄存器的说法?网上有说法说是寄存器占两个字节,但线圈的最少操作单位是位。类似于继电器的通断状态,直接根据电…...

【MySQL】函数
文章目录1. DQL执行顺序2. 函数2.1 字符串函数2.2 数值函数2.3 日期函数2.4 流程函数2.5 窗口函数2.5.1 介绍2.5.2 聚合窗口函数2.5.3 排名窗口函数2.5.4 取值窗口函数1. DQL执行顺序 2. 函数 2.1 字符串函数 函数功能concat(s1,s2,…sn)字符串拼接,将s1,s2…sn拼…...
MySQL高级
一、基础环境搭建 环境准备:CentOS7.6(系统内核要求是3.10以上的)、FinalShell 1. 安装Docker 帮助文档 : https://docs.docker.com/ 1、查看系统内核(系统内核要求是3.10以上的) uname -r2、如果之前安装过旧版本的D…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

python/java环境配置
环境变量放一起 python: 1.首先下载Python Python下载地址:Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个,然后自定义,全选 可以把前4个选上 3.环境配置 1)搜高级系统设置 2…...

【HTML-16】深入理解HTML中的块元素与行内元素
HTML元素根据其显示特性可以分为两大类:块元素(Block-level Elements)和行内元素(Inline Elements)。理解这两者的区别对于构建良好的网页布局至关重要。本文将全面解析这两种元素的特性、区别以及实际应用场景。 1. 块元素(Block-level Elements) 1.1 基本特性 …...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...

篇章二 论坛系统——系统设计
目录 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 1. 数据库设计 1.1 数据库名: forum db 1.2 表的设计 1.3 编写SQL 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 通过需求分析获得概念类并结合业务实现过程中的技术需要&#x…...

链式法则中 复合函数的推导路径 多变量“信息传递路径”
非常好,我们将之前关于偏导数链式法则中不能“约掉”偏导符号的问题,统一使用 二重复合函数: z f ( u ( x , y ) , v ( x , y ) ) \boxed{z f(u(x,y),\ v(x,y))} zf(u(x,y), v(x,y)) 来全面说明。我们会展示其全微分形式(偏导…...
