【笔记】原子结构的近代理论

近代原子结构理论的建立是从氢原子光谱得到启示的。

一、氢原子光谱与波尔理论

1.氢原子光谱

在装有两个电极的真空玻璃管内通入极少量高纯氢气，通高压电使之放电，管中发出的光束通过分光棱镜，得到分立的谱线，称为线状光谱。

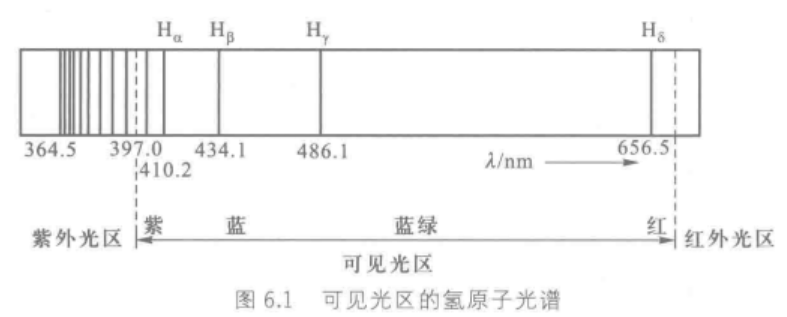
发现氢原子光谱中谱线的频率满足里德伯方程式：$\nu =3.29\times 10^{15}(\frac{1}{n_1^2}-\frac{1}{n_2^2}),n_1>n_2$

为了解释氢原子光谱，把普朗克的量子论应用于卢瑟福的含核原子模型，得到玻尔原子模型。

2.波尔原子模型

1. 电子在核外只能沿着特定的轨道而不是任意圆轨道运动，在这些轨道上运动的电子不放出也不吸收能量。

   求电子绕核运动的轨道半径：$r_n=a_0{n}^2$，n是主量子数，$a_0=53pm$，称为玻尔半径。

   求电子能量：$E=-\frac{2.18\times 10^{-18}}{n^2}$

   在通常情况下，电子尽可能在离核最近、能量最低的n=1轨道上运动，处于“基态”；电子在其他轨道上运动，处于“激发态”；$n=\infty ,E_{\infty }=0$，电子被电离成为自由电子。

2. 原子中的电子由一个轨道跃迁到另一个轨道时才会放出或吸收能量。若能量以光辐射的形式出现，其频率取决于两个轨道之间的能极差。

​ $h\nu =E_{n_2}-E_{n_1}$

​ 推出氢原子光谱的频率是$\nu =3.29\times 10^{15}(\frac{1}{n_1^2}-\frac{1}{n_2^2})$

波尔理论虽然成功解释了氢原子光谱，但是不能解释多电子原子的光谱甚至不能解释氢原子光谱的精细结构。

它没有完全冲破经典物理的束缚，没有意识到电子运动的特性——波粒二象性，因此不能全面反映微观粒子的运动规律。

二、微观粒子运动的波粒二象性和统计规律

光的干涉、衍射——波动性

光电效应——粒子性

德布罗意认为电子也和光子一样具有波动性，通过德布罗意关系式计算波长：$\lambda =\frac{h}{mv}$

电子在晶体上的衍射证实了德布罗意预言，在屏幕上产生圆环衍射。

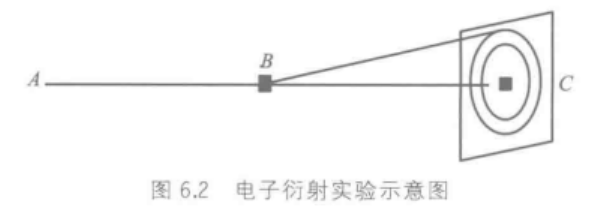
德布罗意波/物质波：微观粒子具有的波。

三、薛定谔方程和波函数

为了描述核外电子运动状态而建立的薛定谔方程，形式是一个二阶偏微分方程。

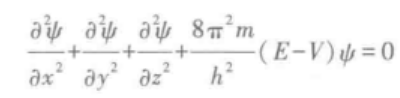
其中x、y、z表示电子的空间直角坐标；m是电子的质量；E是系统总能量；V是核对电子的吸引能，即势能；ψ是三维坐标x、y、z的函数，称为波函数。

薛定谔方程的意义：每一个合理解ψ就代表该微粒运动的某一种可能，对应的E就是该定态对应的能级。

波函数ψ近似认为核外电子可能出现的区域，被称为原子轨道，又称原子轨函（和宏观轨道区别）。

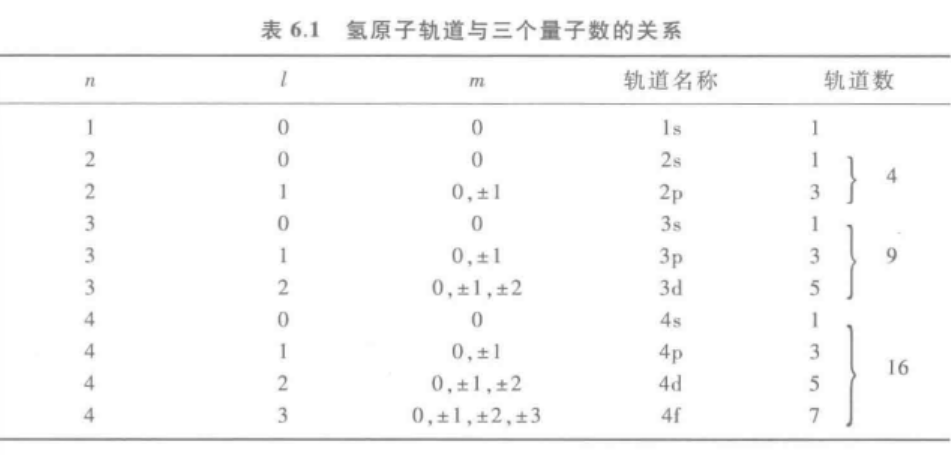
1.四个量子数及含义

求解薛定谔方程不仅可以导出E和n，还可以导出三个量子数：主量子数n、角量子数l、磁量子数m

当这三个量子数确定，波函数ψ才有合理解。故n、l、m三量子数被称为轨道量子数。

（1）主量子数n

n是决定原子轨道能级的主要参数，表示不同的电子主层。

n的数值越大，电子的能量越高，电子离核距离越远。

n=1，2，……正整数

通常用K、L、M、N、O、P表示电子层：

主量子数n	1	2	3	4	5	6	…
电子层	K	L	M	N	O	P	…

能量高低顺序： K<L<M<N<O<P<…

（2）角量子数l

在高分辨分光镜下，可以观察到一些元素原子光谱的一条粗谱线由多条很靠近的细谱线构成，说明同一电子层内电子的运动状态和能量不是完全相同，这是因为不同的原子轨道，同一电子层还可以分成几个不同的亚层。

l是反映原子轨道形状的参数。

l取值受n的限制。l=0,1,2,…,n-1正整数

亚层符号为s,p,d,f

角量子数l	0	1	2	3	……
亚层符号	s	p	d	f	…
原子轨道形状	球形	哑铃形	梅花瓣型	（无解）	…

（3）磁量子数m

激发态原子在外磁场作用下，原来的一条谱线还可以分裂成若干条，这是由于同一个亚层可以有多个原子轨道（只有空间伸展方向不同的区别）。

m是用来描述原子轨道在空间伸展方向的参数。

m取值受l的制约，取值范围为：[-l,l]的整数值

简并轨道/等价轨道：亚层中具有的方向不同的轨道在没有外加磁场的情况下，具有相同的能量。

（4）自旋量子数$m_s$

$m_s$用来描述电子运动的自旋方向。

$m_s$只有两种可能的取值，$\pm \frac{1}{2}$，通常用向上↑或向下↓的箭头表示。

自旋反平行：两个电子处于不同的自旋状态，可用符号"↑↓","↓↑"表示。

自旋平行：两个电子处于相同的自旋状态，用符号“↑↑”或“↓↓”表示。

2.原子轨道的角度分布图

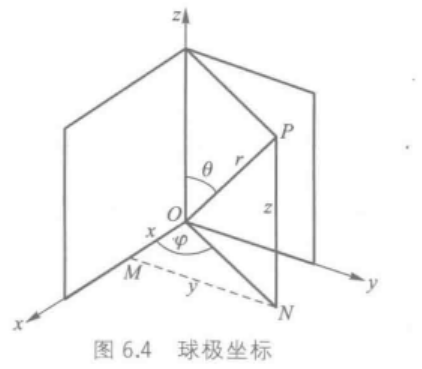
ψ既可以用直角坐标ψ(x,y,z)表示，也可以变换成球极坐标ψ(r,θ,φ)表示。
$$\begin{gathered} x=rsin\theta cos\varphi \\ y=rsin\theta sin\varphi \\ z=rcos\theta \\ \psi (r,\theta ,\varphi )=R(r)\cdot Y(\theta ,\varphi ) \end{gathered}$$
其中，$R(r)$代表径向部分，$Y(\theta ,\varphi )$代表原子轨道的角度部分。

已知波函数如下：

1s轨道

$Y_{1s}$取值是定值$\sqrt{\frac{1}{4\pi }}$，跟角度没关系，所以它们的角度分布图是一个半径为$\sqrt{\frac{1}{4\pi }}$的球面，$Y_{1s}$值在各个方向相同。

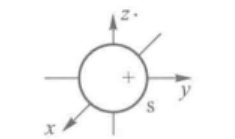
所有s轨道波函数都跟1s相同，都为$\sqrt{\frac{1}{4\pi }}$，所以角度分布图都是半径为$\sqrt{\frac{1}{4\pi }}$的球面。

$2p_z$轨道

$Y_{p_z}=\sqrt{\frac{3}{4\pi }}cos\theta$

在球坐标中作图，可得到两个相切于原点的球面，即为$p_z$轨道的角度分布图。

另外两个$p_x$，$p_y$形状和$p_z$相同，只是空间取向不同。

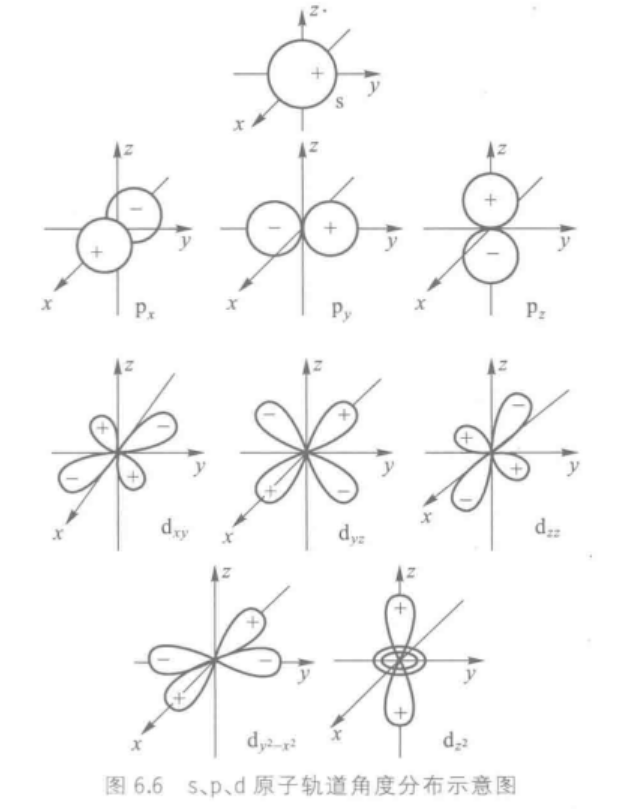
四、电子云

1.电子云与概率密度

概率密度：电子在原子核外空间某位置上单位体积出现的概率大小。

在光学中，光的强度与电磁场强度的绝对值平方成正比，类比到电子，就是在原子核外某处空间发现电子的概率密度ρ和电子波在此处的强度ψ的绝对值的平方成正比，$\rho \propto |\psi {|}^2$

在研究中，有实际意义的是相对密度而非绝对密度，故只需要考虑电子波在此处的强度的平方即可，用$|\psi {|}^2$表示核外电子出现的概率密度。

2.电子云角度分布图

电子云的图形可以类比原子轨道，分为两部分（径向+角度）

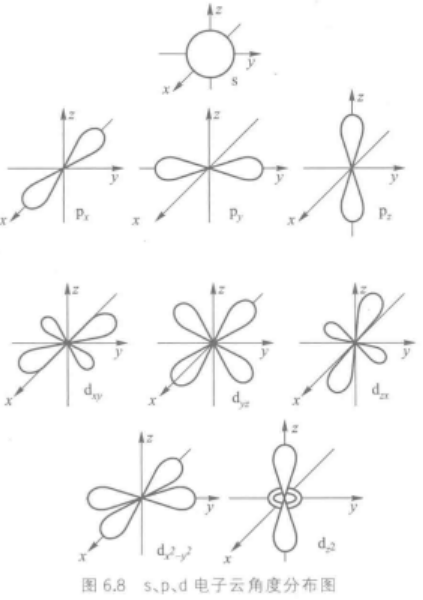
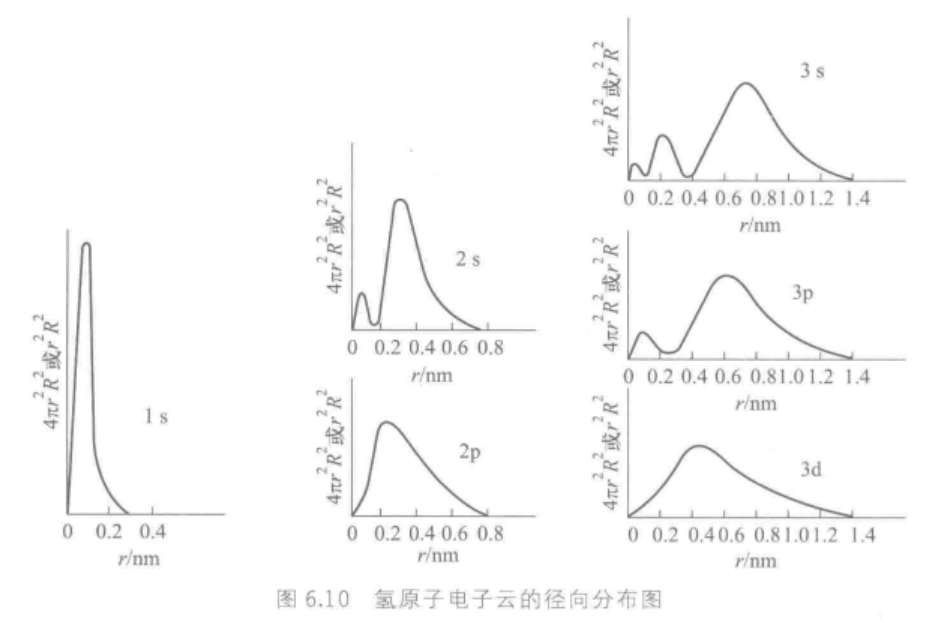
3.电子云径向分布图

电子云角度分布图只能表现出电子在空间不同角度出现的概率大小，不能表现电子出现概率和离核远近的关系，所以需要电子云径向分布图。

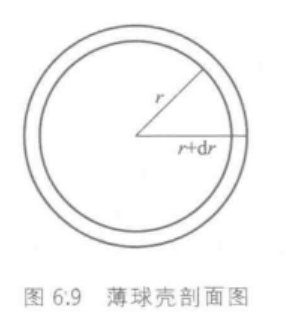
电子云径向分布图：在半径为r，厚度为dr的球壳，电子出现的概率（即$4\pi r^2{R}^{2}dr$或$r^2{R}^{2}dr$的大小）。以$4\pi r^2{R}^{2}dr$对r作图得到。

$4\pi r^2{R}^{2}dr$数值越大，表示电子在半径为r的球壳中出现的概率越大。

从电子云径向分布看出：n增大时，电子离核平均距离增大；当n相同，电子离核平均距离接近。