【Lcode 随笔】C语言版看了不后悔系列持续更新中。。。

文章目录
- 题目一:最长回文子串
- 题目描述:
- 示例输入与输出:
- 题目分析:
- 解题思路:
- 示例代码:
- 深入剖析:
- 题目二:合并K个有序链表
- 题目描述:
- 示例输入与输出:
- 题目分析:
- 解题思路:
- 示例代码:
- 深入剖析:
- 题目三:全排列
- 题目描述:
- 示例输入与输出:
- 题目分析:
- 解题思路:
- 示例代码:
- 深入剖析:
🌈你好呀!我是 山顶风景独好
🎈欢迎踏入我的博客世界,能与您在此邂逅,真是缘分使然!😊
🌸愿您在此停留的每一刻,都沐浴在轻松愉悦的氛围中。
📖这里不仅有丰富的知识和趣味横生的内容等您来探索,更是一个自由交流的平台,期待您留下独特的思考与见解。🌟
🚀让我们一起踏上这段探索与成长的旅程,携手挖掘更多可能,共同进步!💪✨
题目一:最长回文子串
题目描述:
给定一个字符串 s,找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。
示例输入与输出:
输入:s = “babad”
输出:“bab” 或 “aba”
输入:s = “cbbd”
输出:“bb”
题目分析:
回文串是指正读和反读都相同的字符串。解决这个问题的关键在于如何高效地找到最长的回文子串。暴力解法的时间复杂度为O(n^3),显然不可取。我们可以考虑使用动态规划或中心扩展法来优化。
解题思路:
动态规划:定义一个二维数组dp,其中dp[i][j]表示字符串s从索引i到j的子串是否为回文。通过填充这个数组,我们可以找到最长的回文子串。
中心扩展法:遍历字符串中的每个字符和每对相邻字符作为回文中心,然后向外扩展以找到最长的回文子串。
这里我们选择中心扩展法,因为它的实现更简洁且时间复杂度为O(n^2),适合本题的要求。
示例代码:
#include <stdio.h>
#include <string.h>
#include <stdlib.h> char* longestPalindrome(char* s) { int len = strlen(s); if (len < 2) return s; int start = 0, maxLen = 1; for (int i = 0; i < len; i++) { int len1 = expandAroundCenter(s, i, i); // 奇数长度回文中心 int len2 = expandAroundCenter(s, i, i + 1); // 偶数长度回文中心 int len = len1 > len2 ? len1 : len2; if (len > maxLen) { start = i - (len - 1) / 2; maxLen = len; } } char* result = (char*)malloc((maxLen + 1) * sizeof(char)); strncpy(result, s + start, maxLen); result[maxLen] = '\0'; return result;
} int expandAroundCenter(char* s, int left, int right) { while (left >= 0 && right < strlen(s) && s[left] == s[right]) { left--; right++; } return right - left - 1;
} int main() { char s1[] = "babad"; char* result1 = longestPalindrome(s1); printf("Longest palindrome in \"%s\" is \"%s\"\n", s1, result1); free(result1); char s2[] = "cbbd"; char* result2 = longestPalindrome(s2); printf("Longest palindrome in \"%s\" is \"%s\"\n", s2, result2); free(result2); return 0;
}
深入剖析:
中心扩展法的核心思想是以每个字符或每对相邻字符为中心,向外扩展以找到最长的回文子串。这种方法避免了不必要的比较,从而提高了效率。
题目二:合并K个有序链表
题目描述:
给定一个链表数组,每个链表都已经按升序排列。合并所有链表,并返回合并后的有序链表。
示例输入与输出:
输入:[[1,4,5],[1,3,4],[2,6]]
输出:1 -> 1 -> 2 -> 3 -> 4 -> 4 -> 5 -> 6
输入:[]
输出:[]
题目分析:
这个问题可以通过逐个合并链表来解决,但效率较低。更优的方法是使用最小堆(优先队列)来维护当前所有链表中的最小元素,从而依次取出最小元素构建合并后的链表。
解题思路:
创建一个最小堆,并将所有链表的头节点加入堆中。
重复以下步骤,直到堆为空:
从堆中取出最小元素作为当前节点。
如果当前节点的下一个节点存在,则将其加入堆中。
将当前节点添加到合并后的链表中。
示例代码:
#include <stdio.h>
#include <stdlib.h> typedef struct ListNode { int val; struct ListNode* next;
} ListNode; // 最小堆节点结构定义
typedef struct MinHeapNode { ListNode* node; struct MinHeapNode* left; struct MinHeapNode* right; struct MinHeapNode* parent;
} MinHeapNode; // 最小堆结构定义
typedef struct MinHeap { MinHeapNode** array; int size; int capacity;
} MinHeap; // 辅助函数:比较两个节点值的大小
int compare(ListNode* a, ListNode* b) { return (a->val > b->val) - (a->val < b->val);
} // 创建最小堆
MinHeap* createMinHeap(int size) { MinHeap* minHeap = (MinHeap*)malloc(sizeof(MinHeap)); minHeap->capacity = size; minHeap->size = 0; minHeap->array = (MinHeapNode**)malloc(size * sizeof(MinHeapNode*)); return minHeap;
} // 释放最小堆内存
void freeMinHeap(MinHeap* minHeap) { for (int i = 0; i < minHeap->size; i++) { free(minHeap->array[i]); } free(minHeap->array); free(minHeap);
} // 插入节点到最小堆
void insertMinHeap(MinHeap* minHeap, ListNode* node) { if (minHeap->size == minHeap->capacity) { printf("Heap is full, cannot insert new node.\n"); return; } MinHeapNode* newNode = (MinHeapNode*)malloc(sizeof(MinHeapNode)); newNode->node = node; newNode->left = NULL; newNode->right = NULL; newNode->parent = NULL; int i = minHeap->size; minHeap->array[i] = newNode; minHeap->size++; // 上浮调整 while (i && compare(minHeap->array[(i - 1) / 2]->node, node) > 0) { MinHeapNode* temp = minHeap->array[i]; minHeap->array[i] = minHeap->array[(i - 1) / 2]; minHeap->array[(i - 1) / 2] = temp; if (minHeap->array[i]->left) { minHeap->array[i]->left->parent = minHeap->array[(i - 1) / 2]; } if (minHeap->array[i]->right) { minHeap->array[i]->right->parent = minHeap->array[(i - 1) / 2]; } minHeap->array[(i - 1) / 2]->parent = minHeap->array[i]; i = (i - 1) / 2; }
} // 提取最小节点
ListNode* extractMin(MinHeap* minHeap) { if (minHeap->size == 0) { printf("Heap is empty, cannot extract minimum node.\n"); return NULL; } ListNode* minNode = minHeap->array[0]->node; MinHeapNode* lastNode = minHeap->array[minHeap->size - 1]; minHeap->array[0] = lastNode; minHeap->size--; // 下沉调整 int i = 0; while (2 * i + 1 < minHeap->size) { int leftChild = 2 * i + 1; int rightChild = 2 * i + 2; int smallest = i; if (compare(minHeap->array[leftChild]->node, minHeap->array[smallest]->node) < 0) { smallest = leftChild; } if (rightChild < minHeap->size && compare(minHeap->array[rightChild]->node, minHeap->array[smallest]->node) < 0) { smallest = rightChild; } if (smallest != i) { MinHeapNode* temp = minHeap->array[i]; minHeap->array[i] = minHeap->array[smallest]; minHeap->array[smallest] = temp; if (minHeap->array[i]->left) { minHeap->array[i]->left->parent = minHeap->array[i]; } if (minHeap->array[i]->right) { minHeap->array[i]->right->parent = minHeap->array[i]; } if (minHeap->array[smallest]->left) { minHeap->array[smallest]->left->parent = minHeap->array[smallest]; } if (minHeap->array[smallest]->right) { minHeap->array[smallest]->right->parent = minHeap->array[smallest]; } i = smallest; } else { break; } } free(lastNode); return minNode;
} // 检查堆是否为空
int isEmpty(MinHeap* minHeap) { return minHeap->size == 0;
} // 获取堆的大小
int getSize(MinHeap* minHeap) { return minHeap->size;
} // 辅助函数:创建新链表节点
ListNode* createNode(int val) { ListNode* newNode = (ListNode*)malloc(sizeof(ListNode)); newNode->val = val; newNode->next = NULL; return newNode;
} // 辅助函数:打印链表
void printList(ListNode* head) { ListNode* current = head; while (current != NULL) { printf("%d -> ", current->val); current = current->next; } printf("NULL\n");
} // 主函数:合并K个有序链表
ListNode* mergeKLists(ListNode** lists, int listsSize) { if (listsSize == 0) return NULL; MinHeap* minHeap = createMinHeap(listsSize); for (int i = 0; i < listsSize; i++) { if (lists[i] != NULL) { insertMinHeap(minHeap, lists[i]); } } ListNode dummy = {0, NULL}; ListNode* tail = &dummy; while (!isEmpty(minHeap)) { ListNode* minNode = extractMin(minHeap); tail->next = minNode; tail = tail->next; if (minNode->next != NULL) { insertMinHeap(minHeap, minNode->next); } } freeMinHeap(minHeap); return dummy.next;
} int main() { ListNode* l1 = createNode(1); l1->next = createNode(4); l1->next->next = createNode(5); ListNode* l2 = createNode(1); l2->next = createNode(3); l2->next->next = createNode(4); ListNode* l3 = createNode(2); l3->next = createNode(6); ListNode* lists[] = {l1, l2, l3}; int listsSize = 3; ListNode* mergedList = mergeKLists(lists, listsSize); printList(mergedList); return 0;
}
深入剖析:
使用最小堆可以有效地合并K个有序链表,因为堆能够始终提供当前所有链表中的最小元素。这种方法的时间复杂度为O(N log K),其中N是所有链表中节点的总数,K是链表的数量。
题目三:全排列
题目描述:
给定一个没有重复数字的序列,返回其所有可能的全排列。
示例输入与输出:
输入:[1,2,3]
输出:[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]
输入:[0,1]
输出:[[0,1],[1,0]]
题目分析:
全排列问题是一个经典的回溯算法问题。回溯算法通过递归和剪枝来搜索所有可能的解。
解题思路:
定义一个递归函数,该函数接收当前排列和剩余可选数字作为参数。
在每次递归调用中,选择一个数字加入当前排列,并从剩余可选数字中移除该数字。
当剩余可选数字为空时,将当前排列加入结果集中。
递归调用该函数,直到所有可能的排列都被找到。
示例代码:
#include <stdio.h>
#include <stdlib.h> // 动态数组结构定义
typedef struct { int* data; int size; int capacity;
} IntArray; // 辅助函数:创建动态数组
IntArray* createIntArray(int capacity) { IntArray* array = (IntArray*)malloc(sizeof(IntArray)); array->data = (int*)malloc(capacity * sizeof(int)); array->size = 0; array->capacity = capacity; return array;
} // 辅助函数:向动态数组添加元素
void append(IntArray* array, int val) { if (array->size >= array->capacity) { array->capacity *= 2; array->data = (int*)realloc(array->data, array->capacity * sizeof(int)); } array->data[array->size++] = val;
} // 辅助函数:释放动态数组内存
void freeIntArray(IntArray* array) { free(array->data); free(array);
} // 主函数:生成全排列
int** permute(int* nums, int numsSize, int* returnSize, int** returnColumnSizes) { *returnSize = 0; IntArray* numsArray = createIntArray(numsSize); for (int i = 0; i < numsSize; i++) { append(numsArray, nums[i]); } IntArray* path = createIntArray(numsSize); IntArray* used = createIntArray(numsSize); for (int i = 0; i < numsSize; i++) { used->data[i] = 0; } int* returnColumnSizesArray = (int*)malloc(numsSize * sizeof(int)); int** result = (int**)malloc(numsSize * numsSize * sizeof(int*)); // 回溯函数 void permuteHelper(IntArray* nums, IntArray* path, IntArray* used, IntArray** result, int* returnSize) { if (path->size == nums->size) { IntArray* temp = createIntArray(path->size); for (int i = 0; i < path->size; i++) { append(temp, path->data[i]); } result[*returnSize] = temp->data; (*returnSize)++; freeIntArray(temp); return; } for (int i = 0; i < nums->size; i++) { if (used->data[i]) continue; used->data[i] = 1; append(path, nums->data[i]); permuteHelper(nums, path, used, result, returnSize); used->data[i] = 0; path->size--; } } permuteHelper(numsArray, path, used, result, returnSize); for (int i = 0; i < *returnSize; i++) { returnColumnSizesArray[i] = path->size; } *returnColumnSizes = returnColumnSizesArray; freeIntArray(numsArray); freeIntArray(path); freeIntArray(used); return result;
} // 辅助函数:打印二维数组
void printPermutations(int** permutations, int permutationsSize, int* returnColumnSizes) { for (int i = 0; i < permutationsSize; i++) { for (int j = 0; j < returnColumnSizes[i]; j++) { printf("%d ", permutations[i][j]); } printf("\n"); }
} int main() { int nums1[] = {1, 2, 3}; int numsSize1 = sizeof(nums1) / sizeof(nums1[0]); int* returnColumnSizes1; int returnSize1; int** permutations1 = permute(nums1, numsSize1, &returnSize1, &returnColumnSizes1); printPermutations(permutations1, returnSize1, returnColumnSizes1); int nums2[] = {0, 1}; int numsSize2 = sizeof(nums2) / sizeof(nums2[0]); int* returnColumnSizes2; int returnSize2; int** permutations2 = permute(nums2, numsSize2, &returnSize2, &returnColumnSizes2); printPermutations(permutations2, returnSize2, returnColumnSizes2); return 0;
}
深入剖析:
回溯算法通过递归和剪枝来搜索所有可能的解空间。在全排列问题中,我们使用三个动态数组来分别存储原始数字、当前排列和已使用数字的状态。通过递归地选择数字并更新状态,我们可以找到所有可能的全排列。
✨ 这就是今天要分享给大家的全部内容了,我们下期再见!😊
🏠 我在CSDN等你哦!我的主页😍
相关文章:

【Lcode 随笔】C语言版看了不后悔系列持续更新中。。。
文章目录 题目一:最长回文子串题目描述:示例输入与输出:题目分析:解题思路:示例代码:深入剖析: 题目二:合并K个有序链表题目描述:示例输入与输出:题目分析&am…...

排序--希尔排序
希尔排序介绍 希尔排序核心思想就是:1,分组;2,直接插入排序:越有序越快 希尔排序就是多次利用直接插入排序的一个排序算法. 希尔排序的算法思想:间隔式分组,利用直接插入排序让组内有序,然后缩小分组再次排序,直到组数为1希尔排序的理论基础就是直接插入排序越有序越快; 希尔排…...
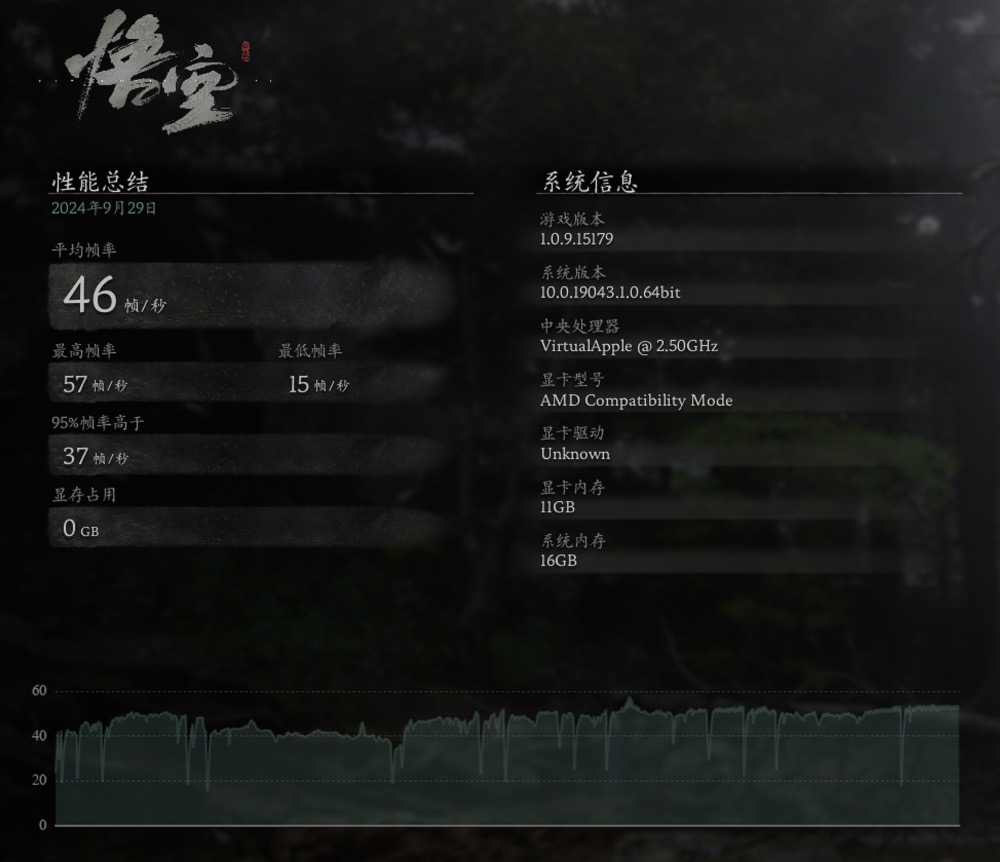
【教程】57帧! Mac电脑流畅运行黑神话悟空
转载请注明出处:小锋学长生活大爆炸[xfxuezhagn.cn] 如果本文帮助到了你,欢迎[点赞、收藏、关注]哦~ 1、先安装CrossOver。网上有许多和谐版,可自行搜索。(pd虚拟机里运行黑神话估计够呛的) 2、运行CrossOver…...

『大模型笔记』Docker如何清理Build Cache!
Docker如何清理Build Cache! 文章目录 一. docker system df1. 镜像(Images)2. 容器(Containers)3. 本地卷(Local Volumes)4. 构建缓存(Build Cache)5. 总结二. 构建缓存(Build Cache)删除有什么影响1. 镜像构建速度变慢2. 磁盘空间被释放3. 不会影响已构建和运行的…...

如何使用 Python 读取数据量庞大的 excel 文件
使用 pandas.read_excel 读取大文件时,的确会遇到性能瓶颈,特别是对于10万行20列这种规模的 .xlsx 文件,常规的 pandas 方法可能会比较慢。 要提高读取速度,关键是找到更高效的方式处理 Excel 文件,特别是在 Python 的…...

c语言200例 067
大家好,欢迎来到无限大的频道 今天给大家带来的是c语言200例 题目要求: 设计一个共用体类型,使其成员包含多种数据类型,根据不同的数据类型,输出不同的结果 要设计一个共用体(union)类型&…...

RabbitMQ的高级特性-死信队列
死信(dead message) 简单理解就是因为种种原因, ⽆法被消费的信息, 就是死信. 有死信, ⾃然就有死信队列. 当消息在⼀个队列中变成死信之后,它能被重新被发送到另⼀个交换器 中,这个交换器就是DLX( Dead Letter Exchange ), 绑定DLX的队列, 就称为死信队…...

Python 复制PDF中的页面
操作PDF文档时,复制其中的指定页面可以帮助我们从PDF文件中提取特定信息,如文本、图表或数据等,以便在其他文档中使用。复制PDF页面也可以实现在不同文件中提取页面,以创建一个新的综合文档。 本文将介绍如何使用Python 在同一文档…...

Sql Developer日期显示格式设置
默认时间格式显示 设置时间格式:工具->首选项->数据库->NLS->日期格式: DD-MON-RR 修改为: YYYY-MM-DD HH24:MI:SS 设置完格式显示:...

IP地址与智能家居能够碰撞出什么样的火花呢?
感应灯、远程遥控空调,自动感应窗帘——智能家居已经在正逐步走入我们的生活,为我们带来前所未有的便捷与舒适体验。而在这一进程中,IP地址又能够与智能家居碰撞出什么样的火花呢? 一、IP地址:智能家居的连接基石 智…...

人工智能技术在电磁场与微波技术专业的应用
在人工智能与计算电磁学的融合背景下,电磁学的研究和应用正在经历一场革命。计算电磁 学是研究电磁场和电磁波在不同介质中的传播、散射和辐射等问题的学科,它在通信、雷达、无 线能量传输等领域具有广泛的应用。随着人工智能技术的发展,这一…...

The First项目报告:探索Yield Guild Games运行机制与发展潜力
在探索数字娱乐与金融融合的全新疆域中,GameFi(游戏化金融)以其独特的魅力引领了一场前所未有的变革。这一创新概念,最初由MixMarvel的CSO Mary Ma在2019年底乌镇大会的远见卓识中首次提出,它将去中心化金融࿰…...

完成UI界面的绘制
绘制UI 接上文,在Order90Canvas下创建Image子物体,图片资源ui_fish_lv1,设置锚点(CountdownPanelImg同理),命名为LvPanelImg,创建Text子物体,边框宽高各50, ,重名为LvT…...

iot网关是什么?iot网关在工业领域的应用-天拓四方
一、IoT网关的定义 IoT网关,即物联网网关,是物联网(IoT)系统中的重要组成部分。它主要实现感知网络与通信网络,以及不同类型感知网络之间的协议转换,既能够支持广域互联,也能满足局域互联的需求…...
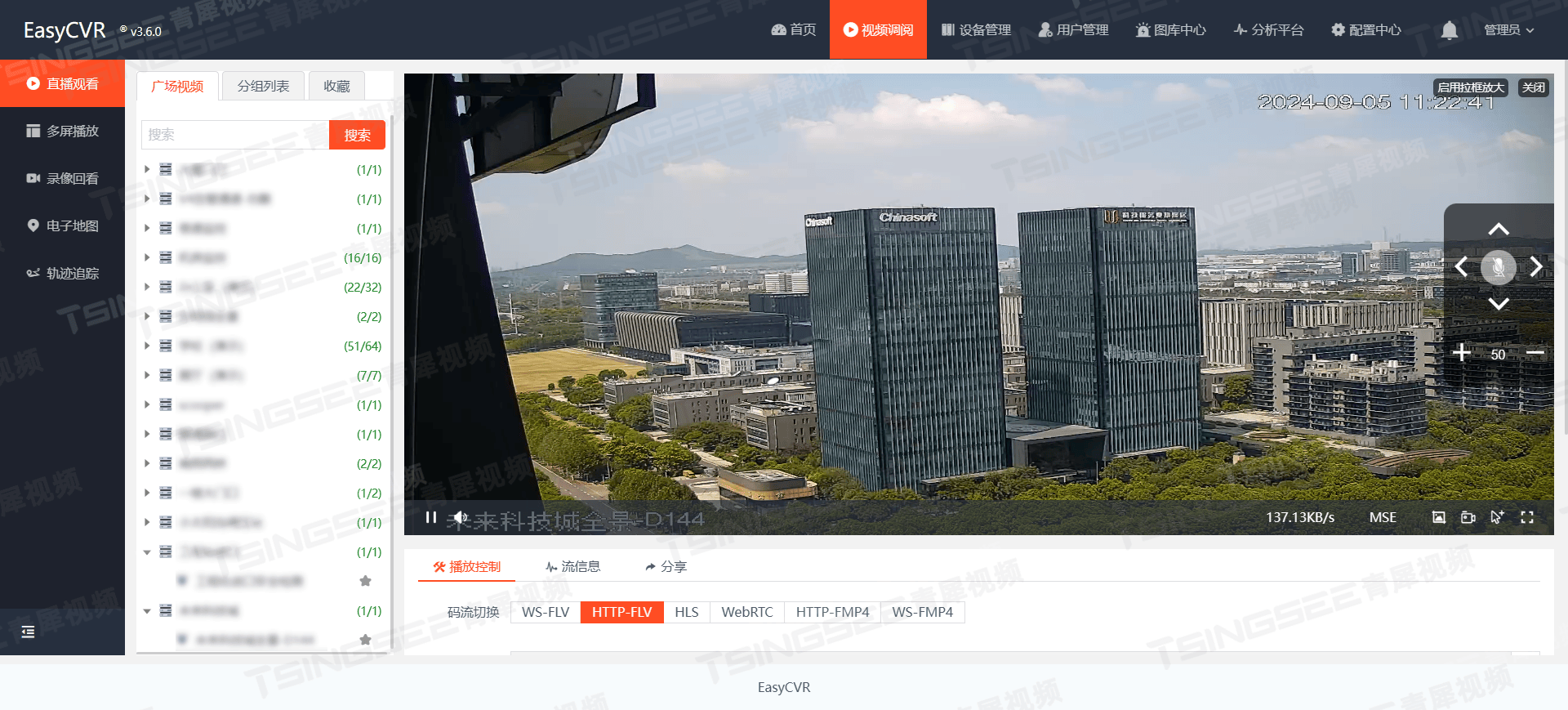
从碎片到整合:EasyCVR平台如何重塑城市感知系统的视频数据生态
随着城市化进程的加速,城市感知系统作为智慧城市的重要组成部分,正逐步成为提升城市管理效率、保障公共安全、优化资源配置的关键手段。EasyCVR视频汇聚融合平台,凭借其强大的数据整合、智能分析与远程监控能力,在城市感知系统中扮…...

java socket bio 改造为 netty nio
公司早些时候接入一款健康监测设备,由于业务原因近日把端口暴露在公网后,每当被恶意连接时系统会创建大量线程,在排查问题是发现是使用了厂家提供的服务端demo代码,在代码中使用的是java 原生socket,在发现连接后使用独…...

进程、线程、协程详解:并发编程的三大武器
在现代计算机科学中,并发编程是一个核心概念,而进程、线程和协程是实现并发的三种主要方式。本文将深入探讨这三种概念,分析它们的特点、优缺点,以及适用场景。 1. 进程 (Process) 1.1 定义 进程是计算机中的程序关于某数据集合上的一次运行活动,是系统进行资源分配和调度的…...

探索5 大 Node.js 功能
目录 单线程 Node.js 工作线程【Worker Threads】 Node.js 进程 进程缺点 工作线程 注意 集群进程模块【Cluster Process Module】 内部发生了什么? 为什么要使用集群 注意: 应用场景: 内置 HTTP/2 支持 这个 HTTP/2 是什么&…...

EZUIKit.js萤石云vue项目使用
EZUIKit.js 是萤石云(Ezviz)提供的一款用于Web端的视频播放和控制的JavaScript库。它允许开发者在网页上轻松集成视频监控、对讲、录像回放等功能,适用于安防监控、智能家居等场景。通过EZUIKit.js,你可以方便地访问萤石云平台上的…...

【Linux】磁盘分区挂载网络配置进程【更详细,带实操】
Linux全套讲解系列,参考视频-B站韩顺平,本文的讲解更为详细 目录 一、磁盘分区挂载 1、磁盘分区机制 2、增加磁盘应用实例 3、磁盘情况查询 4、磁盘实用指令 二、网络配置 1、NAT网络原理图 2、网络配置指令 3、网络配置实例 4、主机名和host…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

Linux 下 DMA 内存映射浅析
序 系统 I/O 设备驱动程序通常调用其特定子系统的接口为 DMA 分配内存,但最终会调到 DMA 子系统的dma_alloc_coherent()/dma_alloc_attrs() 等接口。 关于 dma_alloc_coherent 接口详细的代码讲解、调用流程,可以参考这篇文章,我觉得写的非常…...

密码学基础——SM4算法
博客主页:christine-rr-CSDN博客 专栏主页:密码学 📌 【今日更新】📌 对称密码算法——SM4 目录 一、国密SM系列算法概述 二、SM4算法 2.1算法背景 2.2算法特点 2.3 基本部件 2.3.1 S盒 2.3.2 非线性变换 编辑…...
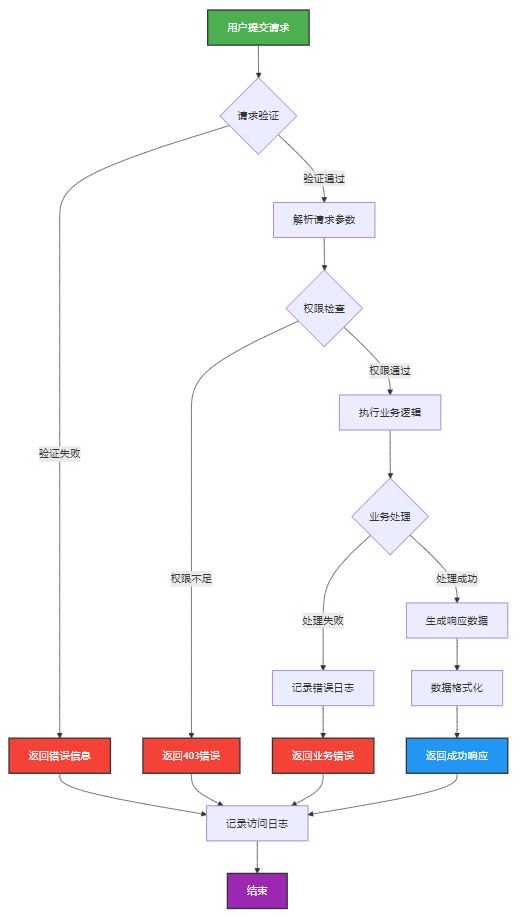
如何做好一份技术文档?从规划到实践的完整指南
如何做好一份技术文档?从规划到实践的完整指南 🌟 嗨,我是IRpickstars! 🌌 总有一行代码,能点亮万千星辰。 🔍 在技术的宇宙中,我愿做永不停歇的探索者。 ✨ 用代码丈量世界&…...

使用ch340继电器完成随机断电测试
前言 如图所示是市面上常见的OTA压测继电器,通过ch340串口模块完成对继电器的分路控制,这里我编写了一个脚本方便对4路继电器的控制,可以设置开启时间,关闭时间,复位等功能 软件界面 在设备管理器查看串口号后&…...
