LeetCode 2535.数组元素和与数字和的绝对差:模拟
【LetMeFly】2535.数组元素和与数字和的绝对差:模拟
力扣题目链接:https://leetcode.cn/problems/difference-between-element-sum-and-digit-sum-of-an-array/
给你一个正整数数组 nums 。
- 元素和 是
nums中的所有元素相加求和。 - 数字和 是
nums中每一个元素的每一数位(重复数位需多次求和)相加求和。
返回 元素和 与 数字和 的绝对差。
注意:两个整数 x 和 y 的绝对差定义为 |x - y| 。
示例 1:
输入:nums = [1,15,6,3] 输出:9 解释: nums 的元素和是 1 + 15 + 6 + 3 = 25 。 nums 的数字和是 1 + 1 + 5 + 6 + 3 = 16 。 元素和与数字和的绝对差是 |25 - 16| = 9 。
示例 2:
输入:nums = [1,2,3,4] 输出:0 解释: nums 的元素和是 1 + 2 + 3 + 4 = 10 。 nums 的数字和是 1 + 2 + 3 + 4 = 10 。 元素和与数字和的绝对差是 |10 - 10| = 0 。
提示:
1 <= nums.length <= 20001 <= nums[i] <= 2000
解题方法:模拟
写一个函数getSum(x)返回整数x在十进制下的每位之和:
int getSum(int x) {int ans = 0;while (x > 0) {ans += x % 10;x /= 10;}return ans;
}
使用两个变量x和y分别记录元素之和和元素每一位之和,遍历一遍原始数组即可得到这个值。
最终,返回abs(x - y)即为答案。
- 时间复杂度 O ( l e n ( n u m s ) × log M ) O(len(nums)\times \log M) O(len(nums)×logM),其中 M M M是 n u m s [ i ] nums[i] nums[i]可取值范围的最大值 2000 2000 2000。
- 空间复杂度 O ( 1 ) O(1) O(1)
AC代码
C++
class Solution {
private:int getSum(int n) {int ans = 0;while (n) {ans += n % 10;n /= 10;}return ans;}
public:int differenceOfSum(vector<int>& nums) {int x = 0, y = 0;for (int t : nums) {x += t, y += getSum(t);}return abs(x - y);}
};
Go
package mainfunc abs(x int) int {if x >= 0 {return x}return -x
}func getSum(x int) int {ans := 0for x > 0 {ans += x % 10x /= 10}return ans
}func differenceOfSum(nums []int) int {x, y := 0, 0for _, t := range nums {x += ty += getSum(t)}return abs(x - y)
}
Java
class Solution {private int getSum(int t) {int ans = 0;while (t > 0) {ans += t % 10;t /= 10;}return ans;}public int differenceOfSum(int[] nums) {int x = 0, y = 0;for (int t : nums) {x += t;y += getSum(t);}return Math.abs(x - y);}
}
Python
from typing import Listclass Solution:def getSum(self, x: int) -> int:ans = 0while x:ans += x % 10x //= 10return ansdef differenceOfSum(self, nums: List[int]) -> int:x = y = 0for t in nums:x += ty += self.getSum(t)return abs(x - y)
同步发文于CSDN和我的个人博客,原创不易,转载经作者同意后请附上原文链接哦~
Tisfy:https://letmefly.blog.csdn.net/article/details/142568318
相关文章:

LeetCode 2535.数组元素和与数字和的绝对差:模拟
【LetMeFly】2535.数组元素和与数字和的绝对差:模拟 力扣题目链接:https://leetcode.cn/problems/difference-between-element-sum-and-digit-sum-of-an-array/ 给你一个正整数数组 nums 。 元素和 是 nums 中的所有元素相加求和。数字和 是 nums 中每…...

SpringCloud-pom创建Eureka
<?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.org/POM/4.0.0 https://…...

动态规划算法专题(一):斐波那契数列模型
目录 1、动态规划简介 2、算法实战应用【leetcode】 2.1 题一:第N个泰波那契数 2.1.1 算法原理 2.1.2 算法代码 2.1.3 空间优化原理——滚动数组 2.1.4 算法代码——空间优化版本 2.2 题二:三步问题 2.2.1 算法原理 2.2.2 算法代码 2.3 题二&a…...

H.264编解码工具 - x264
一、简介 x264是一个开源的H.264/AVC视频编码库,它可以将视频数据压缩成H.264格式,并且可以从H.264格式解码出原始视频数据。 x264是以C语言编写的,并且可以在多个平台上使用,包括Windows、Linux和Mac OS等操作系统。 x264具有很高的编码效率和视频质量,它支持多种编码…...

外卖点餐小程序源码系统 单店多门店自助切换 带完整的安装代码包以及搭建部署教程
系统概述 本外卖点餐小程序源码系统旨在帮助餐饮企业和商家快速搭建一个功能完善的在线外卖平台。系统支持单店与多门店的灵活切换,方便商家根据自身业务需求进行管理和运营。同时,系统还提供了丰富的营销工具和数据分析功能,助力商家实现精…...

通过Ideal和gitbash共同实现分支合并
文章目录 背景描述:演示jy_20240704_develop分支同步到jy_dev分支方式一方式二 背景描述: 目前项目里有四个分支,分别是master、jy_20240704_develop、jy_dev、jy_qas。 其中master是主分支,其他三个分支都是根据master来创建的…...

Vue.js 组件开发
Vue.js 是一个渐进式的JavaScript框架,主要用于构建用户界面。它采用了组件化的开发方式,使得前端开发更加高效、灵活且易于维护。组件是Vue.js的核心概念之一,理解和掌握组件的开发,有助于我们高效地构建现代Web应用。 本文将涵…...

【Lcode 随笔】C语言版看了不后悔系列持续更新中。。。
文章目录 题目一:最长回文子串题目描述:示例输入与输出:题目分析:解题思路:示例代码:深入剖析: 题目二:合并K个有序链表题目描述:示例输入与输出:题目分析&am…...

排序--希尔排序
希尔排序介绍 希尔排序核心思想就是:1,分组;2,直接插入排序:越有序越快 希尔排序就是多次利用直接插入排序的一个排序算法. 希尔排序的算法思想:间隔式分组,利用直接插入排序让组内有序,然后缩小分组再次排序,直到组数为1希尔排序的理论基础就是直接插入排序越有序越快; 希尔排…...
【教程】57帧! Mac电脑流畅运行黑神话悟空
转载请注明出处:小锋学长生活大爆炸[xfxuezhagn.cn] 如果本文帮助到了你,欢迎[点赞、收藏、关注]哦~ 1、先安装CrossOver。网上有许多和谐版,可自行搜索。(pd虚拟机里运行黑神话估计够呛的) 2、运行CrossOver…...

『大模型笔记』Docker如何清理Build Cache!
Docker如何清理Build Cache! 文章目录 一. docker system df1. 镜像(Images)2. 容器(Containers)3. 本地卷(Local Volumes)4. 构建缓存(Build Cache)5. 总结二. 构建缓存(Build Cache)删除有什么影响1. 镜像构建速度变慢2. 磁盘空间被释放3. 不会影响已构建和运行的…...

如何使用 Python 读取数据量庞大的 excel 文件
使用 pandas.read_excel 读取大文件时,的确会遇到性能瓶颈,特别是对于10万行20列这种规模的 .xlsx 文件,常规的 pandas 方法可能会比较慢。 要提高读取速度,关键是找到更高效的方式处理 Excel 文件,特别是在 Python 的…...

c语言200例 067
大家好,欢迎来到无限大的频道 今天给大家带来的是c语言200例 题目要求: 设计一个共用体类型,使其成员包含多种数据类型,根据不同的数据类型,输出不同的结果 要设计一个共用体(union)类型&…...

RabbitMQ的高级特性-死信队列
死信(dead message) 简单理解就是因为种种原因, ⽆法被消费的信息, 就是死信. 有死信, ⾃然就有死信队列. 当消息在⼀个队列中变成死信之后,它能被重新被发送到另⼀个交换器 中,这个交换器就是DLX( Dead Letter Exchange ), 绑定DLX的队列, 就称为死信队…...

Python 复制PDF中的页面
操作PDF文档时,复制其中的指定页面可以帮助我们从PDF文件中提取特定信息,如文本、图表或数据等,以便在其他文档中使用。复制PDF页面也可以实现在不同文件中提取页面,以创建一个新的综合文档。 本文将介绍如何使用Python 在同一文档…...

Sql Developer日期显示格式设置
默认时间格式显示 设置时间格式:工具->首选项->数据库->NLS->日期格式: DD-MON-RR 修改为: YYYY-MM-DD HH24:MI:SS 设置完格式显示:...

IP地址与智能家居能够碰撞出什么样的火花呢?
感应灯、远程遥控空调,自动感应窗帘——智能家居已经在正逐步走入我们的生活,为我们带来前所未有的便捷与舒适体验。而在这一进程中,IP地址又能够与智能家居碰撞出什么样的火花呢? 一、IP地址:智能家居的连接基石 智…...

人工智能技术在电磁场与微波技术专业的应用
在人工智能与计算电磁学的融合背景下,电磁学的研究和应用正在经历一场革命。计算电磁 学是研究电磁场和电磁波在不同介质中的传播、散射和辐射等问题的学科,它在通信、雷达、无 线能量传输等领域具有广泛的应用。随着人工智能技术的发展,这一…...

The First项目报告:探索Yield Guild Games运行机制与发展潜力
在探索数字娱乐与金融融合的全新疆域中,GameFi(游戏化金融)以其独特的魅力引领了一场前所未有的变革。这一创新概念,最初由MixMarvel的CSO Mary Ma在2019年底乌镇大会的远见卓识中首次提出,它将去中心化金融࿰…...

完成UI界面的绘制
绘制UI 接上文,在Order90Canvas下创建Image子物体,图片资源ui_fish_lv1,设置锚点(CountdownPanelImg同理),命名为LvPanelImg,创建Text子物体,边框宽高各50, ,重名为LvT…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...

相关类相关的可视化图像总结
目录 一、散点图 二、气泡图 三、相关图 四、热力图 五、二维密度图 六、多模态二维密度图 七、雷达图 八、桑基图 九、总结 一、散点图 特点 通过点的位置展示两个连续变量之间的关系,可直观判断线性相关、非线性相关或无相关关系,点的分布密…...

如何把工业通信协议转换成http websocket
1.现状 工业通信协议多数工作在边缘设备上,比如:PLC、IOT盒子等。上层业务系统需要根据不同的工业协议做对应开发,当设备上用的是modbus从站时,采集设备数据需要开发modbus主站;当设备上用的是西门子PN协议时…...

基于Uniapp的HarmonyOS 5.0体育应用开发攻略
一、技术架构设计 1.混合开发框架选型 (1)使用Uniapp 3.8版本支持ArkTS编译 (2)通过uni-harmony插件调用原生能力 (3)分层架构设计: graph TDA[UI层] -->|Vue语法| B(Uniapp框架)B --&g…...
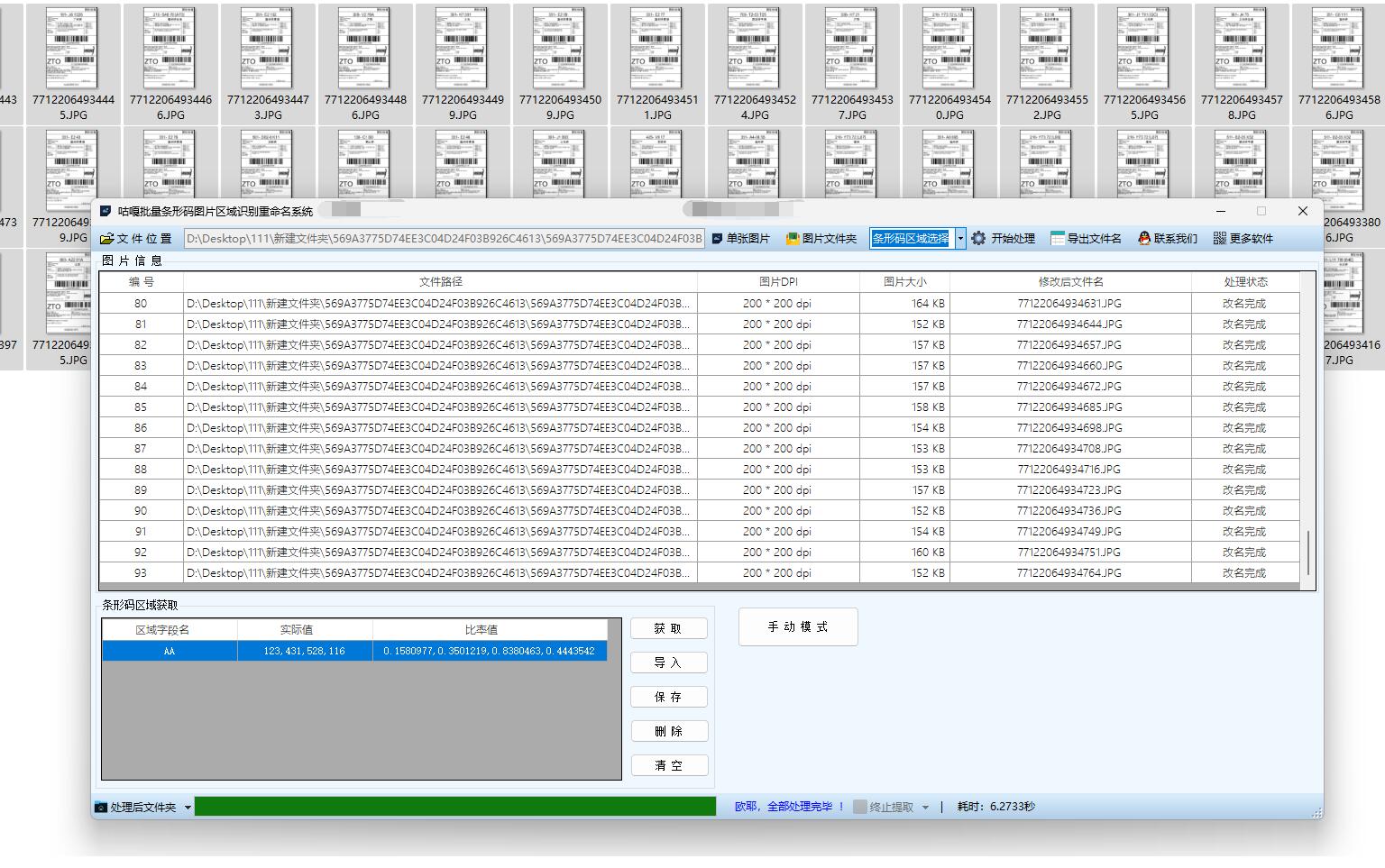
【工具教程】多个条形码识别用条码内容对图片重命名,批量PDF条形码识别后用条码内容批量改名,使用教程及注意事项
一、条形码识别改名使用教程 打开软件并选择处理模式:打开软件后,根据要处理的文件类型,选择 “图片识别模式” 或 “PDF 识别模式”。如果是处理包含条形码的 PDF 文件,就选择 “PDF 识别模式”;若是处理图片文件&…...
