【无标题】logistic映射
当Logistic映射中的控制参数 μ \mu μ 为负数时,系统的行为与正数 μ \mu μ 的情况截然不同。Logistic映射的一般形式是:
x ( t + 1 ) = μ x ( t ) ( 1 − x ( t ) ) x(t+1) = \mu x(t) (1 - x(t)) x(t+1)=μx(t)(1−x(t))其中 x ( t ) x(t) x(t) 表示时间步 t t t 的状态值, μ \mu μ 是控制参数。对于 μ < 0 \mu < 0 μ<0 的情况,我们可以分析其动态行为:### 数学分析1. 固定点分析: - 对于 μ < 0 \mu < 0 μ<0,我们可以通过设置 x ( t + 1 ) = x ( t ) = x ∗ x(t+1) = x(t) = x^* x(t+1)=x(t)=x∗ 来找到系统的固定点。代入 Logistic 映射公式,我们得到: x ∗ = μ x ∗ ( 1 − x ∗ ) x^* = \mu x^* (1 - x^*) x∗=μx∗(1−x∗) μ x ∗ − μ x ∗ 2 = x ∗ \mu x^* - \mu x^{*2} = x^* μx∗−μx∗2=x∗ μ x ∗ − μ x ∗ 2 − x ∗ = 0 \mu x^* - \mu x^{*2} - x^* = 0 μx∗−μx∗2−x∗=0 x ∗ ( μ − μ x ∗ − 1 ) = 0 x^* (\mu - \mu x^* - 1) = 0 x∗(μ−μx∗−1)=0 - 这个方程有两个解: x ∗ = 0 x^* = 0 x∗=0 和 x ∗ = μ − 1 μ x^* = \frac{\mu - 1}{\mu} x∗=μμ−1。然而,由于 μ < 0 \mu < 0 μ<0,第二个解将不在 [0, 1] 区间内(除非 μ = 1 \mu = 1 μ=1,但这是不可能的因为 μ < 0 \mu < 0 μ<0),因此只有 x ∗ = 0 x^* = 0 x∗=0 是合理的解。2. 稳定性分析: - 对于 x ∗ = 0 x^* = 0 x∗=0,我们可以通过计算导数来判断其稳定性。导数为: ∣ f ′ ( x ∗ ) ∣ = ∣ μ − 2 μ x ∗ ∣ |f'(x^*)| = |\mu - 2\mu x^*| ∣f′(x∗)∣=∣μ−2μx∗∣ 在 x ∗ = 0 x^* = 0 x∗=0 处,这变为: ∣ μ − 2 μ ⋅ 0 ∣ = ∣ μ ∣ |\mu - 2\mu \cdot 0| = |\mu| ∣μ−2μ⋅0∣=∣μ∣ - 如果 ∣ μ ∣ < 1 |\mu| < 1 ∣μ∣<1(即 − 1 < μ < 0 -1 < \mu < 0 −1<μ<0),则固定点是稳定的。如果 ∣ μ ∣ > 1 |\mu| > 1 ∣μ∣>1(即 μ < − 1 \mu < -1 μ<−1),则固定点是不稳定的。### 结论当 μ < 0 \mu < 0 μ<0 时,Logistic映射的动态行为主要由固定点 x ∗ = 0 x^* = 0 x∗=0 控制。如果 − 1 < μ < 0 -1 < \mu < 0 −1<μ<0,这个固定点是稳定的,系统会趋向于这个状态。如果 μ < − 1 \mu < -1 μ<−1,固定点是不稳定的,系统的行为将更加复杂和不可预测。在实际应用中,通常只考虑 μ > 0 \mu > 0 μ>0 的情况,因为负值的 μ \mu μ 在实际生物或经济系统中较少见。
当Logistic映射中的参数μ大于4时,系统的行为会变得非常复杂且难以预测。在数学上,Logistic映射定义为:
x ( t + 1 ) = μ x ( t ) ( 1 − x ( t ) ) x(t+1) = \mu x(t) (1 - x(t)) x(t+1)=μx(t)(1−x(t))其中, x ( t ) x(t) x(t) 是时间步 t t t 的状态值, μ \mu μ 是控制参数。当 μ > 4 \mu > 4 μ>4 时,系统的动态行为超出了传统的倍周期分岔和混沌区域,进入了一个被称为“混沌海”的区域。在这个区域中,系统的行为变得极其敏感依赖于初始条件,即使是微小的变化也会导致完全不同的长期行为。### 数学分析在 μ > 4 \mu > 4 μ>4 的情况下,Logistic映射的迭代结果通常会迅速发散到无穷大或负无穷大,因为方程中的非线性项 ( 1 − x ( t ) ) (1 - x(t)) (1−x(t)) 会导致 x ( t ) x(t) x(t) 的值在每次迭代中迅速增大或减小。这意味着,对于大多数实际应用来说,当 μ > 4 \mu > 4 μ>4 时,Logistic映射不再具有实际的物理意义或应用价值。### 应用领域的影响在生态学、经济学和其他使用Logistic映射来模拟动态系统的领域中,通常不会考虑 μ > 4 \mu > 4 μ>4 的情况,因为这个范围内的行为过于极端和不稳定,无法有效反映现实世界的动态过程。在这些领域,研究者更倾向于关注 μ \mu μ 在 [3, 4] 区间内的行为,这个区间内系统表现出丰富的动态行为,包括倍周期分岔和混沌。### 结论总的来说,当变化率(即控制参数 μ \mu μ)大于4时,Logistic映射的系统行为变得非常复杂且通常不具有实际的应用价值。这种情况在理论研究中可能具有数学上的兴趣,但在实际应用中需要谨慎处理。
逻辑映射公式通常指的是Logistic映射,其数学表达式为:x(t+1) = μx(t)(1-x(t))。以下是对这一公式的详细解释:
- 参数说明: - x(t):在时间步t时的状态值,范围通常在[0, 1]之间。 - μ:控制参数,也称为分支参数,影响系统的行为。μ的取值范围是[0, 4]。 - t:迭代的时间步。2. 动力学行为: - 当0 < μ ≤ 1时,系统会趋向于一个固定点0,即无论初始条件如何,最终x(t)都会趋向于0[3]。 - 当1 < μ < 3时,系统会趋向于一个非零的稳定点,具体值取决于μ的大小[3]。 - 当3 ≤ μ < 3.5699456时,系统会进入倍周期分岔的阶段,表现出复杂的周期性行为[2]。 - 当3.5699456 < μ ≤ 4时,系统进入混沌状态,表现出非周期、不收敛和对初始条件极度敏感的特性[1][3]。3. 应用领域: - Logistic映射不仅在数学和物理学中被广泛研究,还在生态学、经济学、工程学等多个领域有重要应用。例如,在生态学中,它可以用来模拟种群的增长和动态变化[2]。 - 在加密技术中,Logistic映射因其生成序列的伪随机性和对初值的敏感性,被用于设计流密码系统[5]。总的来说,Logistic映射是一个简单但功能强大的数学模型,它能够展示出从简单规则到复杂行为的过渡。通过调整参数μ和初始值x₀,可以观察到从稳定点到混沌状态的转变,这使得Logistic映射成为研究非线性动力学和混沌理论的一个重要工具。
相关文章:

【无标题】logistic映射
当Logistic映射中的控制参数 μ \mu μ 为负数时,系统的行为与正数 μ \mu μ 的情况截然不同。Logistic映射的一般形式是: x ( t 1 ) μ x ( t ) ( 1 − x ( t ) ) x(t1) \mu x(t) (1 - x(t)) x(t1)μx(t)(1−x(t))其中 x ( t ) x(t) x(t) 表示时…...

基于Node.js+Express+MySQL+VUE科研成果网站发布查看科研信息科研成果论文下载免费安装部署
目录 1.技术选型 2.功能设计 3.系统架构 4.开发流程 5.开发背景 6.开发目标 7.技术可行性 8.功能可行性 8.1功能图 8.2 界面设计 8.3 部分代码 构建一个基于Spring Boot、Java Web、J2EE、MySQL数据库以及Vue前后端分离的科研成果网站,可…...

提升C++代码质量的一些建议
文章目录 1. 命名清晰2. 简洁性3. 一致性4. 注释5. 避免复杂性6. 重构7. 测试8. 错误处理9. 文档10. 代码复用11. 性能优化12. 安全性- 代码规范推荐 C开发中,写出优雅且可维护的代码不仅能提升代码质量,还能提高团队协作效率和项目长期的可扩展性。以下…...

起重机防摇摆技术如何达标-武汉正向科技
武汉正向科技防摇摆控制器 主要技术参数 1、防摇摆精度: 0.4 2、行车到达目标位置偏差位置偏差: 25mm 3、通讯方式:PROFINET / PROFIBUS / RS232 / RS422 / RS485; 4、消除载荷的摇摆达 96% 以上; 5、技术先进…...

[大语言模型-论文精读] MoRAG - 基于多部分融合的检索增强型人体动作生成
MoRAG--Multi-Fusion Retrieval Augmented Generation for Human Motion KS Shashank, S Maheshwari, RK Sarvadevabhatla - arXiv preprint arXiv:2409.12140, 2024 MoRAG - 基于多部分融合的检索增强型人体动作生成 1. 目录 MoRAG--Multi-Fusion Retrieval Augmented Generat…...

解决端口被占用
当你被你的编译器提醒, 当前端口被占用, 但明明你的服务什么的都没有启用,这时有三种解决办法: 1 。 重启 。 重启解决80%的问题 2 。 修改你的端口号 。 3 。 去windows命令行中查看,端口占用情况 第一步 …...

【递归】7. leetcode 404 左叶子之和
1 题目描述 题目链接:左叶子之和 2 解答思路 递归分为三步,接下来就按照这三步来思考问题 第一步:挖掘出相同的子问题 (关系到具体函数头的设计) 第二步:只关心具体子问题做了什么 (关系…...

react+antdMobie实现消息通知页面样式
一、实现效果 二、代码 import React, { useEffect, useState } from react; import style from ./style/index.less; import { CapsuleTabs, Ellipsis, Empty, SearchBar, Tag } from antd-mobile; //消息通知页面 export default function Notification(props) {const [opti…...

Git 撤销一个已经push到远端仓库的commit
在 Git 中,撤销一个已经推送到远程仓库的改动有几种不同的方法,具体取决于你是否想要完全删除改动,还是只是恢复文件的某个状态。以下是常见的几种方法: git revert 撤销特定的commit git revert 是最安全的方法,因为…...

lambda表达式底层实现
一、lambda 代码 & 反编译 原始Java代码 假设我们有以下简单的Java程序,它使用Lambda表达式来遍历并打印一个字符串列表: import java.util.Arrays; import java.util.List;public class LambdaExample {public static void main(String[] args) {…...
鸿蒙NEXT开发-组件事件监听和状态管理(基于最新api12稳定版)
注意:博主有个鸿蒙专栏,里面从上到下有关于鸿蒙next的教学文档,大家感兴趣可以学习下 如果大家觉得博主文章写的好的话,可以点下关注,博主会一直更新鸿蒙next相关知识 专栏地址: https://blog.csdn.net/qq_56760790/…...

《More Effective C++》的学习
引用与指针 没有所谓的null reference reference一定需要代表某个对象,所以C要求reference必须有初值。 QString &s; 使用reference可能比使用pointer更高效。 因为reference一定是有效的,而指针可能为空(需要多加一个判断࿰…...

Leetcode面试经典150题-322.零钱兑换
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。 计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。 你可以认为每种硬币的数量是无限的。 示…...

python17_len()函数
len()函数 A B "" C "hello world" D 18 E 18def len_test(s):try:# 尝试计算字符串的长度length len(s)return lengthexcept TypeError:# 如果不是字符串,则返回 None 或者提示错误return Noneif __name__ "__main__":# 单…...
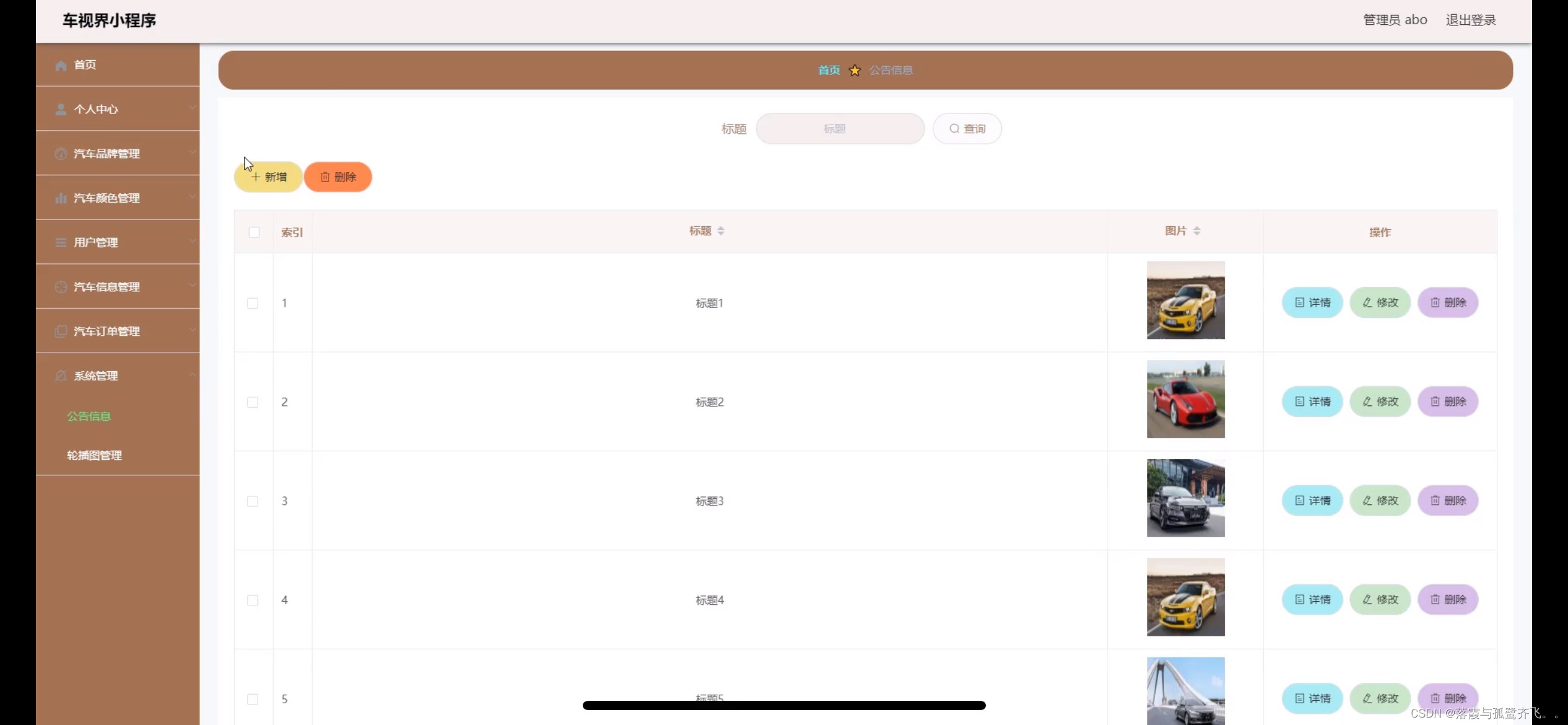
车视界系统小程序的设计
管理员账户功能包括:系统首页,个人中心,汽车品牌管理,汽车颜色管理,用户管理,汽车信息管理,汽车订单管理系统管理 微信端账号功能包括:系统首页,汽车信息,我…...

SQLCMD命令行工具导入数据并生成对应的日志文件
SQLCMD是一个命令行工具,专门用于在Microsoft SQL Server数据库上运行SQL脚本和管理任务。它提供了一种交互式和自动化的方式来执行SQL命令和脚本,并允许用户与SQL Server数据库进行高效的交互。以下是关于SQLCMD的详细介绍: 主要功能 执行SQL脚本: SQLCMD可以执行包含SQL…...

tauri中加载本地文件图片或者下载网络文件图片后存储到本地,然后通过前端页面展示
有一个需求是需要将本地上传的文件或者网络下载的文件存储到本地,并展示在前端页面上的。其实如果只是加载本地文件,然后展示还是挺简单的,可以看我的文章:tauri程序加载本地图片或者文件在前端页面展示-CSDN博客 要想实现上述需…...

QSqlDatabase在多线程中的使用
Qt中多线程使用数据库_qt数据库管理类支持多数据库,多线程-CSDN博客 1. 代码: #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QPushButton> #include <QSqlDatabase> #include <QSqlQuery> #include <QSqlError>…...
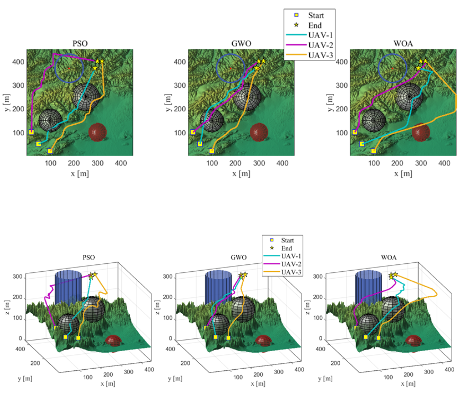
【无人机设计与控制】Multi-UAV|多无人机多场景路径规划算法MATLAB
摘要 本研究探讨了多无人机路径规划问题,提出了三种不同算法的对比分析,包括粒子群优化(PSO)、灰狼优化(GWO)和鲸鱼优化算法(WOA)。利用MATLAB实现了多场景仿真实验,验证…...
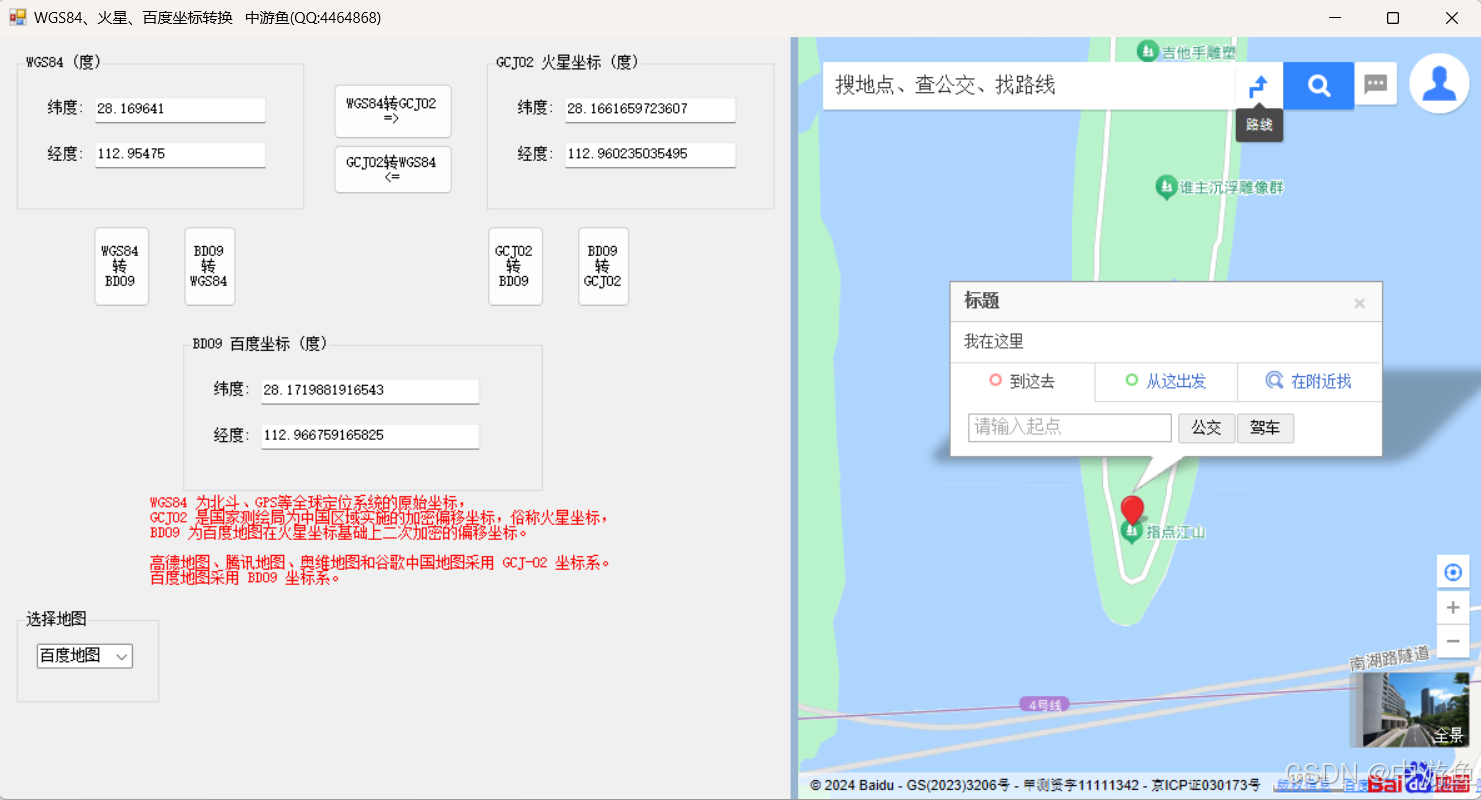
Visual Studio C# 编写加密火星坐标转换
Visual Studio C# 编写加密火星坐标转换 1、WGS84坐标转GCJ02火星坐标2、GCJ02火星坐标转WGS84坐标(回归计算)3、GCJ02火星坐标转BD09百度坐标4、BD09百度坐标转GCJ02火星坐标(回归计算)5、坐标公共转换类6、地图显示7、程序简单界…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

[Java恶补day16] 238.除自身以外数组的乘积
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O(n) 时间复杂度…...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

Python基于历史模拟方法实现投资组合风险管理的VaR与ES模型项目实战
说明:这是一个机器学习实战项目(附带数据代码文档),如需数据代码文档可以直接到文章最后关注获取。 1.项目背景 在金融市场日益复杂和波动加剧的背景下,风险管理成为金融机构和个人投资者关注的核心议题之一。VaR&…...
