动态规划刷题记录(2)
今天的三个题目属于模板题,可能将来会遇见它们的变形应用。
1、最长上升子序列问题
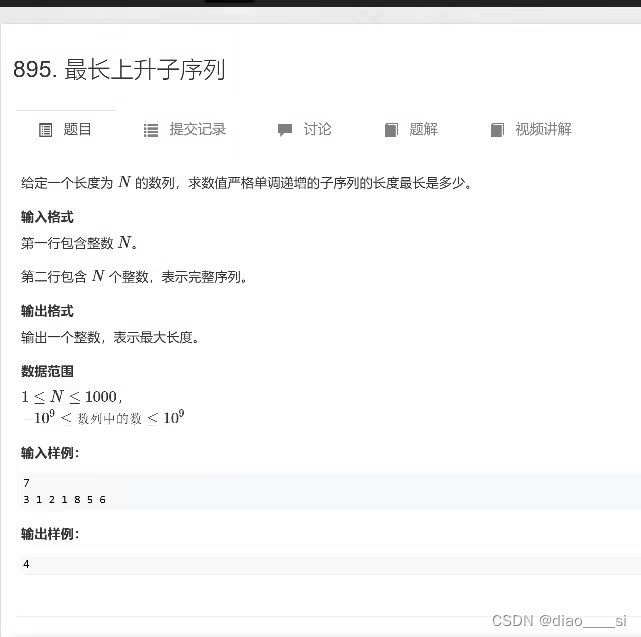
这道题目的关键就在于我们的状态定义,我们定义:f(i)表示长度为i的子序列的末尾最大值。意思就是,比如一个子序列为:1,4,5,那么按我们的集合定义就应该是:f(3) = 5。这样定义了话我们就可以很容易的解题,我们只需要从头到尾遍历数组,找到当前数大于的最小值,然后更新找到的f。举个例子,f(2) = 3 f(3) = 5,这时候我们当前数是4,那么我们就把4接到3之后,也就是f(3) = 4。这里其实用到了贪心的思想,我们让不同长度的末尾值尽可能小,这样最长长度一定会尽可能长。代码你可以直接暴力寻找,也可以二分查找都可以。
#include <iostream>//直接暴力using namespace std;const int N = 1010;
int f[N] ,a[N] ,n;int main()
{cin >> n;for (int i = 1 ;i <= n ;i ++) cin >> a[i];for (int i = 1 ;i <= n ;i ++){f[i] = 1;for (int j = 1 ;j <= i ;j ++){if (a[i] > a[j]) f[i] = max(f[i] ,f[j] + 1);}}int res = -1;for (int i = 1 ;i <= n ;i ++) res = max(res ,f[i]);cout << res;return 0;
}#include <iostream>//二分
#include <cstdio>
#include <algorithm>
#include <cstring>using namespace std;#define N 100100int f[N] ,len ,a[N] ,n;int main()
{cin >> n;for (int i = 1 ;i <= n ; i++) cin >> a[i];f[0] = -2e9;for (int i = 1 ;i <= n ;i ++){int l = 0 ,r = len;while (l < r){int mid = (l + r + 1) / 2;if (a[i] > f[mid]) l = mid;elser = mid - 1;}len = max(len ,r + 1);f[r + 1] = a[i];}cout << len;return 0;
}2、最长公共子序列
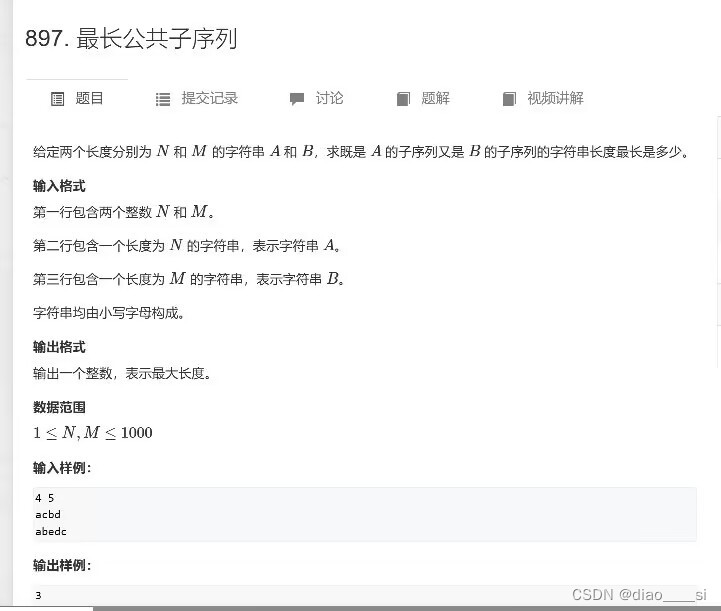
这个题目的dp思路是:定义一个集合f(i ,j)表示字符串A的前i个字符以及字符串B的前j个字符中最长公共字符串长度。状态划分就可以是:1、a[i] == b[j]时,f[i][j] = f[i - 1][j - 1] +1。2、a[i] != b[j]时,最大公共字符串一定在A的前i - 1个字符和B的前j个字符 或者说A的前i个字符和B的前j - 1个字符中,因此,f[i][j] = max(f[i - 1][j] ,f[i][j - 1])。
#include <iostream>
#include <cstdio>
#include <algorithm>
#include <cstring>using namespace std;#define N 1100int f[N][N] ,n ,m;
char a[N] ,b[N];int main()
{cin >> n >>m;scanf("%s" ,a + 1);scanf("%s" ,b + 1);f[0][0] = 0;for (int i = 1 ;i <= n ;i ++)for (int j = 1 ;j <= m ;j ++){if (a[i] == b[j]) f[i][j] = f[i - 1][j - 1] + 1;f[i][j] = max(f[i - 1][j] ,f[i][j]);f[i][j] = max(f[i][j - 1] ,f[i][j]);}cout << f[n][m];return 0;
}3、最长公共上升子序列

这道题的思路是前两道题的结合版本,更加的复杂,很难想到。f(i ,j)表示第一个序列前i个字母以及第二个序列前j个字母,并且以b[j]结尾的公共上升子序列的最大值。那么我们的状态划分就可以分为两大类:一、a[i] != b[j]的时候,最大公共上升序列跟a[i]无关,那么状态转移:f[i][j] = f[i - 1][j]。二、a[i] == b[j]的时候,最大公共上升序列的末尾就是a[i] ,那么我们就根据倒数第二个值是哪一个划分状态,f[i][j] = max(f[i - 1][1] ,f[i - 1][2] .......f[i - 1][j - 1])。根据这个思路我们写出代码:
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>using namespace std;#define N 3500
#define ll long longll f[N][N] ,n ,a[N] ,b[N];int main()
{cin >> n;for (int i = 1 ;i <= n ;i ++) cin >> a[i];for (int j = 1 ;j <= n ;j ++) cin >> b[j];for (int i = 1 ;i <= n ;i ++){for (int j = 1 ;j <= n ;j ++){ll maxv = 1;//作为中间值存取f(i - 1 ,1 ~ j - 1)的最大值f[i][j] = f[i - 1][j];if (a[i] == b[j]){for (int k = 1 ;k < j ;k ++){if (a[i] > b[k]) maxv = max(maxv ,f[i - 1][k] + 1);//注意,必须a[i] > b[k]否则就不能满足递增序列的条件。}f[i][j] = max(f[i][j] ,maxv);}}}ll ans = -1e9;for (int i = 1 ;i <= n ; i ++) ans = max(ans ,f[n][i]);cout << ans;return 0;
}三重循环n方复杂度,很明显时间复杂度太高,我们考虑优化。根据代码我们可以看出,在i确定的情况下,f[i][k - 1]的值是跟j没有关系的,我们就可以优化掉第三层循环:
#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>using namespace std;#define N 3050int f[N][N] ,n ,a[N] ,b[N];int main()
{cin >> n;for (int i = 1 ;i <= n ;i ++) cin >> a[i];for (int j = 1 ;j <= n ;j ++) cin >> b[j];for (int i = 1 ;i <= n ;i ++){int maxv = 1;for (int j = 1 ;j <= n ;j ++){f[i][j] = f[i - 1][j];if (a[i] == b[j]) f[i][j] = max(f[i][j] ,maxv);if (a[i] > b[j]) maxv = max(maxv ,f[i - 1][j] + 1);}}int ans = 0;for (int i = 1 ;i <= n ; i ++) ans = max(ans ,f[n][i]);cout << ans;return 0;
}
相关文章:

动态规划刷题记录(2)
今天的三个题目属于模板题,可能将来会遇见它们的变形应用。 1、最长上升子序列问题 这道题目的关键就在于我们的状态定义,我们定义:f(i)表示长度为i的子序列的末尾最大值。意思就是,比如一个子序列为:1,4,5࿰…...
)
2023年广东省网络安全竞赛——Web 渗透测试解析(超级详细)
任务一:Web 渗透测试 任务环境说明: √ 服务器场景:Server03 √ 服务器场景操作系统:未知(关闭连接) 通过本地 PC 中的渗透测试平台 Kali 对靶机进行 WEB 渗透,找到页面内的文件上传漏洞并且尝试进行上传攻击,将文件上传成功后的页面回显字符串作为Flag 提交(如:…...

MI-SegNet阅读笔记
MI-SegNet: Mutual Information-Based US Segmentation for Unseen Domain Generalization 摘要 解决医学成像泛化能力提出了一种新的基于互信息(MI)的框架MI- segnet分离解剖结构和领域特征采用两个编码器提取相关特征:两个特征映射中出现的任何MI都将受到惩罚&a…...

十、MyBatis分页插件
1.分页插件实现的步骤 ①在pom.xml添加依赖 <dependency><groupId>com.github.pagehelper</groupId><artifactId>pagehelper</artifactId><version>5.2.0</version> </dependency>②配置分页插件 mybatis-config.xml 在MyB…...

EasyCVR平台国标GB28181协议设备接入时,可支持过滤通道类型
EasyCVR基于云边端智能协同架构,能支持海量视频的轻量化接入与集中汇聚管理,平台可支持多协议接入,包括市场主流标准协议与厂家私有协议及SDK,如:国标GB28181、RTMP、RTSP/Onvif、海康Ehome、海康SDK、宇视SDK等&#…...
玩转git的第1章节:git的理论以及操作规则
一 git原理 1.1 git的操作原理 上图是Git与提交有关的三个命令对应的操作: Add命令是把文件从IDE的工作目录添加到本地仓库的stage区, Commit命令把stage区的暂存文件提交到当前分支的仓库,并清空stage区。 Push命令把本地仓库的提交同步…...

【新2023Q2模拟题JAVA】华为OD机试 - 二叉树层次遍历
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南华为od机试,独家整理 已参加机试人员的实战技巧本篇题解:二叉树层次遍历 题目 有一棵…...

轻松拿结果-第三部分 同欲 -第六章 有凝聚力才有战斗力
第三部分 同欲 “上下同欲者胜”,同结果、共承担,不仅是打造销售铁军军魂的必要条件,也能让成员们对每个结果负责,更好更快实现目标。 第六章 有凝聚力才有战斗力 管理者有担当才能上下齐心 苦劳是自己的,功劳是团队的 做管理者,就要做好承受苦劳奉献功劳的心理准备 学…...

chatGPT 会给程序员带来失业潮吗?
AIChatGPT根本不是取代普通人工作,让很多人失业那么简单。他现在直接革的是世界级巨头的命,你从他们的反应就能看出来这个人工智能将掀起一场怎样规模的战争,什么腾讯百度纷纷研发自己的版本,谷歌是直接拉响红色警报,那…...

Vue项目proxyTable跨域配置
Vue项目proxyTable跨域配置文章说明proxyTable跨域配置config / dev.env.jsconfig / prod.env.jsconfig / index.jsutils / request.js接口api.js路径转换解析文章说明 学习连接 - 重要❤ - 一文详解vue-cli2.0与vue-cli3.0之间的区别 1. vue cli 2.0项目2. 本地运行时&#x…...

ubuntu16.04搭建gitlab
ubuntu16.04搭建gitlab 目录ubuntu16.04搭建gitlab一、在虚拟机ubuntu16.04安装gitlab二、配置gitlab三、使用gitlab四、踩坑记录工作中遇到需要在远端服务器搭建gitlab,耗时4天,踩坑无数,特此开个虚拟机再次搭建一次gitlab并记录供以后参考&…...

SSMP综合案例
案例实现方案分析 实体类开发————使用Lombok快速制作实体类 Dao开发————整合MyBatisPlus,制作数据层测试类 Service开发————基于MyBatisPlus进行增量开发,制作业务层测试类 Controller开发————基于Restful开发,使用PostM…...

让你的作品更出色——词云Word Cloud的制作方法(基于python,WordCloud,stylecloud)
让你的作品更出色—— 词云Word Cloud的制作方法(基于python) 本文目录: 一、词云的简介 二、 实现原理和流程 1、制作词云流程图 2、词云实现原理 三、 实现词云的方式 1、安装词云相关模块库 2、WordCloud库 3、stylecloud库 四、总结 一、词…...

axios请求拦截器
在vue项目中,通常使用axios与后台进行数据交互,axios是一款基于promise封装的库, axios特性: 1、axios 是一个基于promise的HTTP库,支持promise所有的API 2、浏览器端/node端(服务器端)都可以…...

四个常见的Linux技术面问题
刚毕业要找工作了,只要是你找工作就会有面试这个环节,那么在面试环节中,有哪些注意事项值得我的关注呢?特别是专业技术岗位,这样的岗位询问一般都是在职的工程师,如何在面试环节更好地理解面试官的问题&…...

有什么适合程序员查资料的网站
当今信息爆炸的时代,程序员每天需要花费大量的时间查找相关技术文档、知识和工具。但是,因为互联网上的内容如此之多,选择合适的网站可以成为一项艰巨的任务。在本文中,我们将介绍几个适合程序员查资料的网站,并详细阐…...
(七)手把手带你搭建精美简洁的个人时间管理网站—实现登录与注册的前端代码【源码】
🌟所属专栏:献给榕榕 🐔作者简介:rchjr——五带信管菜只因一枚 😮前言:该专栏系为女友准备的,里面会不定时发一些讨好她的技术作品,感兴趣的小伙伴可以关注一下~👉文章简…...
Day933.如何将设计最终落地到代码 -系统重构实战
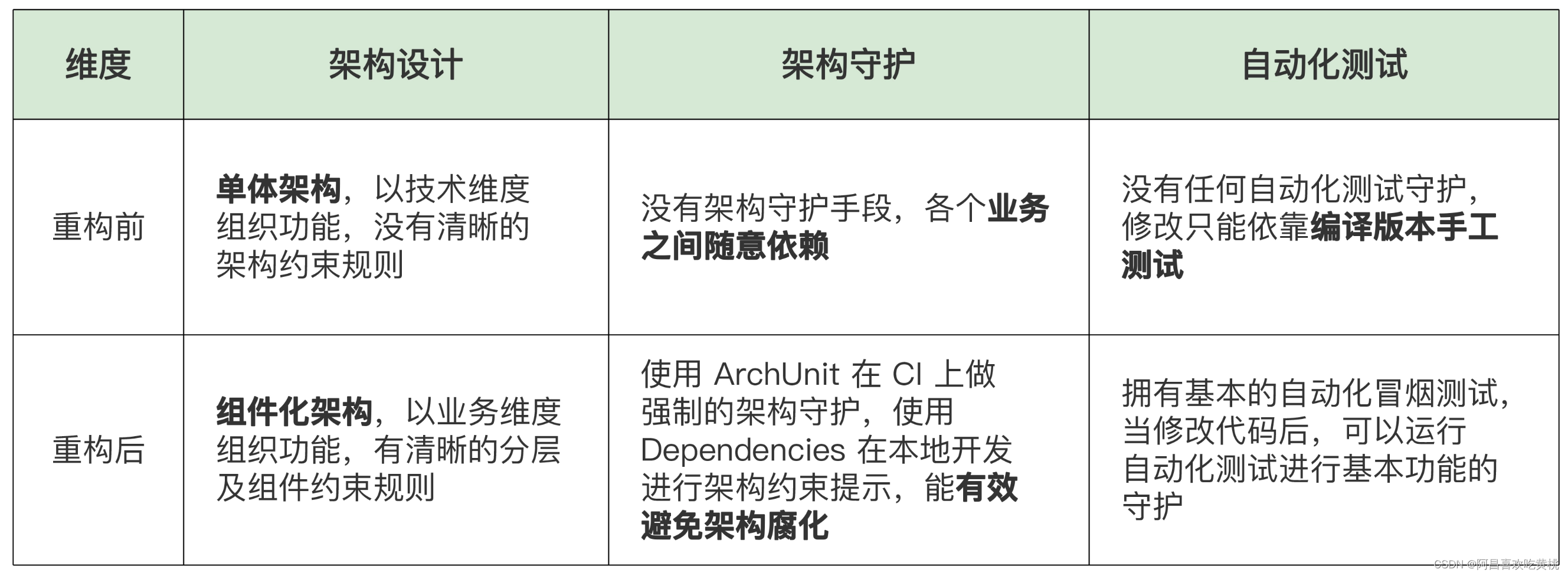
如何将设计最终落地到代码 Hi,我是阿昌,今天学习记录的是关于如何将设计最终落地到代码的内容。 这要将各个组件拆分到独立的模块工程中,最终将架构设计落地到代码中。 组件化架构重构 5 个关键的步骤分别是: 设计守护解耦移动…...
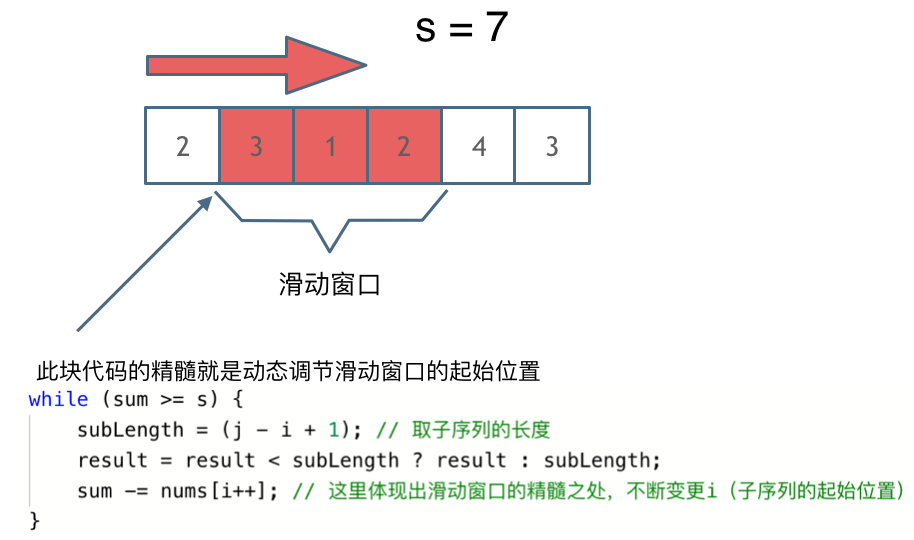
209. 长度最小的子数组
209. 长度最小的子数组 力扣题目链接(opens new window) 给定一个含有 n 个正整数的数组和一个正整数 s ,找出该数组中满足其和 ≥ s 的长度最小的 连续 子数组,并返回其长度。如果不存在符合条件的子数组,返回 0。 示例: 输入…...
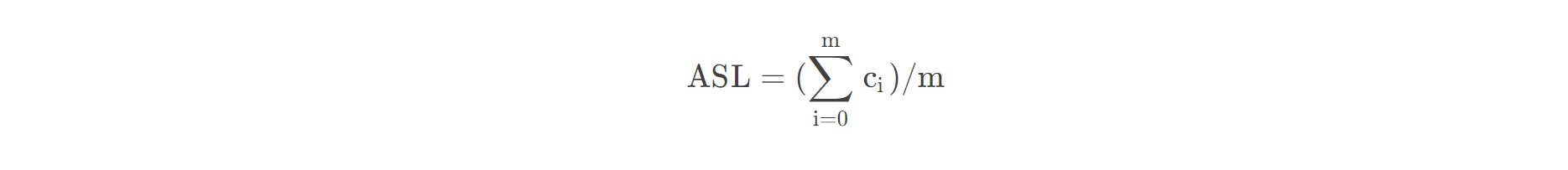
【数据结构与算法】查找(Search)【详解】
文章目录查找查找概论一、查找的基本概念顺序表查找一、定义二、算法有序表查找一、折半查找二、插值查找三、斐波那契查找线性索引查找一、稠密索引二、分块索引三、倒排索引二叉树排序与平衡二叉树一、二叉排序树1、定义2、二叉排序树的常见操作3、性能分析二、平衡二叉树1、…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

FFmpeg 低延迟同屏方案
引言 在实时互动需求激增的当下,无论是在线教育中的师生同屏演示、远程办公的屏幕共享协作,还是游戏直播的画面实时传输,低延迟同屏已成为保障用户体验的核心指标。FFmpeg 作为一款功能强大的多媒体框架,凭借其灵活的编解码、数据…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程(6.3)
目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 编辑编辑 UDP的特征 socke函数 bind函数 recvfrom函数(接收函数) sendto函数(发送函数) 五、网络编程之 UDP 用…...

RKNN开发环境搭建2-RKNN Model Zoo 环境搭建
目录 1.简介2.环境搭建2.1 启动 docker 环境2.2 安装依赖工具2.3 下载 RKNN Model Zoo2.4 RKNN模型转化2.5编译C++1.简介 RKNN Model Zoo基于 RKNPU SDK 工具链开发, 提供了目前主流算法的部署例程. 例程包含导出RKNN模型, 使用 Python API, CAPI 推理 RKNN 模型的流程. 本…...

Linux【5】-----编译和烧写Linux系统镜像(RK3568)
参考:讯为 1、文件系统 不同的文件系统组成了:debian、ubuntu、buildroot、qt等系统 每个文件系统的uboot和kernel是一样的 2、源码目录介绍 目录 3、正式编译 编译脚本build.sh 帮助内容如下: Available options: uboot …...
