【数学分析笔记】第4章第2节 导数的意义和性质(2)
4. 微分
4.2 导数的意义与性质
4.2.3 单侧导数
f ′ ( x ) = lim Δ x → 0 f ( x + Δ x ) − f ( x ) Δ x = lim x → x 0 f ( x ) − f ( x 0 ) x − x 0 f'(x)=\lim\limits_{\Delta x\to 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}=\lim\limits_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0} f′(x)=Δx→0limΔxf(x+Δx)−f(x)=x→x0limx−x0f(x)−f(x0)
f + ′ ( x 0 ) = lim Δ x → 0 + f ( x + Δ x ) − f ( x ) Δ x f'_+(x_0)=\lim\limits_{\Delta x\to 0^+}\frac{f(x+\Delta x)-f(x)}{\Delta x} f+′(x0)=Δx→0+limΔxf(x+Δx)−f(x)为 f f f在 x 0 x_0 x0的右导数。
f − ′ ( x 0 ) = lim Δ x → 0 − f ( x + Δ x ) − f ( x ) Δ x f'_-(x_0)=\lim\limits_{\Delta x\to 0^-}\frac{f(x+\Delta x)-f(x)}{\Delta x} f−′(x0)=Δx→0−limΔxf(x+Δx)−f(x)为 f f f在 x 0 x_0 x0的左导数。
f f f在 x 0 x_0 x0可导 ⇔ f \Leftrightarrow f ⇔f在 x 0 x_0 x0的左右导数存在且相等。
【注】 f + ′ ( x 0 ) f'_+(x_0) f+′(x0)与 f ′ ( x 0 + ) f'(x_0^+) f′(x0+)不同, f + ′ ( x 0 ) f'_+(x_0) f+′(x0)是 f f f在 x 0 x_0 x0的右导数,而 f ′ ( x 0 + ) f'(x_0^+) f′(x0+)是 f f f的导函数在 x 0 x_0 x0的右极限。 f − ′ ( x 0 ) f'_-(x_0) f−′(x0)与 f ′ ( x 0 − ) f'(x_0^-) f′(x0−)的不同也是类似的。
【例4.2.3】考察 f ( x ) = ∣ x ∣ f(x)=|x| f(x)=∣x∣在 x 0 = 0 x_0=0 x0=0的左右导数。
【解】函数图像如下:

当 x > 0 x>0 x>0时, f ( x ) = ∣ x ∣ = x , f + ′ ( 0 ) = lim Δ x → 0 + f ( 0 + Δ x ) − f ( 0 ) Δ x = Δ x Δ x = 1 f(x)=|x|=x,f'_+(0)=\lim\limits_{\Delta x \to 0 ^+}\frac{f(0+\Delta x)-f(0)}{\Delta x}=\frac{\Delta x}{\Delta x}=1 f(x)=∣x∣=x,f+′(0)=Δx→0+limΔxf(0+Δx)−f(0)=ΔxΔx=1
当 x < 0 x<0 x<0时, f ( x ) = ∣ x ∣ = − x , f − ′ ( 0 ) = lim Δ x → 0 − f ( 0 + Δ x ) − f ( 0 ) Δ x = − Δ x Δ x = − 1 f(x)=|x|=-x,f'_-(0)=\lim\limits_{\Delta x \to 0 ^-}\frac{f(0+\Delta x)-f(0)}{\Delta x}=\frac{-\Delta x}{\Delta x}=-1 f(x)=∣x∣=−x,f−′(0)=Δx→0−limΔxf(0+Δx)−f(0)=Δx−Δx=−1
f + ′ ( 0 ) ≠ f − ′ ( 0 ) f'_+(0)\ne f'_-(0) f+′(0)=f−′(0)
则 f ( x ) f(x) f(x)在 0 0 0点不可导。
【例4.2.4】 f ( x ) = { x sin 1 x , x > 0 0 , x ⩽ 0 f(x)=\left\{\begin{array}{cc} x \sin \frac{1}{x}, & x>0 \\ 0, & x \leqslant 0 \end{array}\right. f(x)={xsinx1,0,x>0x⩽0,讨论 f ( x ) f(x) f(x)在 x = 0 x=0 x=0处的可导情况。
【解】函数图像如下:

f − ′ ( 0 ) = lim Δ x → 0 − f ( 0 + Δ x ) − f ( 0 ) Δ x = lim Δ x → 0 − 0 Δ x = 0 f'_-(0)=\lim\limits_{\Delta x \to 0 ^ -}\frac{f(0+\Delta x)-f(0)}{\Delta x}=\lim\limits_{\Delta x \to 0 ^ -}\frac{0}{\Delta x}=0 f−′(0)=Δx→0−limΔxf(0+Δx)−f(0)=Δx→0−limΔx0=0(真0做分母, Δ x → 0 \Delta x\to 0 Δx→0但 Δ x ≠ 0 \Delta x \ne 0 Δx=0
f + ′ ( 0 ) = lim Δ x → 0 + f ( 0 + Δ x ) − f ( 0 ) Δ x = lim Δ x → 0 + Δ x sin 1 Δ x Δ x f'_+(0)=\lim\limits_{\Delta x \to 0 ^ +}\frac{f(0+\Delta x)-f(0)}{\Delta x}=\lim\limits_{\Delta x \to 0 ^ +}\frac{\Delta x\sin \frac{1}{\Delta x}}{\Delta x} f+′(0)=Δx→0+limΔxf(0+Δx)−f(0)=Δx→0+limΔxΔxsinΔx1不存在
则 f f f在 x 0 = 0 x_0=0 x0=0的右导数不存在。
所以 f f f在 0 0 0点不可导
【例4.2.5】 f ( x ) = { x 2 + b , x > 2 , a x + 1 , x ⩽ 2. f(x)=\left\{\begin{array}{ll} x^{2}+b, & x>2, \\ a x+1, & x \leqslant 2 . \end{array}\right. f(x)={x2+b,ax+1,x>2,x⩽2.,要求确定 a , b a,b a,b,使得 f f f在 x 0 = 2 x_0=2 x0=2点可导。
【解】由于可导一定连续
则 f f f在 x 0 = 2 x_0=2 x0=2连续,由题意可知 f f f在 x 0 = 2 x_0=2 x0=2左连续
即 lim x → 2 + f ( x ) = lim x → 2 + ( x 2 + b ) = 4 + b = f ( 2 − ) = 2 a + 1 \lim\limits_{x\to 2^+}f(x)=\lim\limits_{x\to 2^+}(x^2+b)=4+b=f(2-)=2a+1 x→2+limf(x)=x→2+lim(x2+b)=4+b=f(2−)=2a+1…(1)
f − ′ ( 2 ) = lim Δ x → 0 − f ( 2 + Δ x ) − f ( 2 ) Δ x = lim Δ x → 0 − a ( 2 + Δ x ) + 1 − ( 2 a + 1 ) Δ x = a Δ x Δ x = a f'_{-}(2)=\lim\limits_{\Delta x\to 0^-}\frac{f(2+\Delta x)-f(2)}{\Delta x}=\lim\limits_{\Delta x\to 0^-}\frac{a(2+\Delta x)+1-(2a+1)}{\Delta x}=\frac{a\Delta x }{\Delta x}=a f−′(2)=Δx→0−limΔxf(2+Δx)−f(2)=Δx→0−limΔxa(2+Δx)+1−(2a+1)=ΔxaΔx=a
f + ′ ( 2 ) = lim Δ x → 0 + f ( 2 + Δ x ) − f ( 2 ) Δ x = lim Δ x → 0 + ( 2 + Δ x ) 2 + b − ( 2 a + 1 ) Δ x = ( 由 ( 1 ) 式知 ) lim Δ x → 0 + ( 2 + Δ x ) 2 + b − ( 4 + b ) Δ x = lim Δ x → 0 + 4 Δ x + Δ x 2 Δ x = 4 f'_+(2)=\lim\limits_{\Delta x\to 0^+}\frac{f(2+\Delta x)-f(2)}{\Delta x}=\lim\limits_{\Delta x\to 0^+}\frac{(2+\Delta x)^2+b-(2a+1)}{\Delta x}=(由(1)式知)\lim\limits_{\Delta x\to 0^+}\frac{(2+\Delta x)^2+b-(4+b)}{\Delta x}=\lim\limits_{\Delta x\to 0^+}\frac{4\Delta x+ \Delta x^2}{\Delta x}=4 f+′(2)=Δx→0+limΔxf(2+Δx)−f(2)=Δx→0+limΔx(2+Δx)2+b−(2a+1)=(由(1)式知)Δx→0+limΔx(2+Δx)2+b−(4+b)=Δx→0+limΔx4Δx+Δx2=4
要使得 f f f在 x 0 = 2 x_0=2 x0=2处可导 f + ′ ( 2 ) = f − ′ ( 2 ) f'_+(2)=f'_-(2) f+′(2)=f−′(2)
则 a = 4 , b = 5 a=4,b=5 a=4,b=5
4.2.4 区间可导
考虑 f ( x ) f(x) f(x)在 ( a , b ) (a,b) (a,b)上每一点可导,则称 f ( x ) f(x) f(x)在 ( a , b ) (a,b) (a,b)上可导;
若 f ( x ) f(x) f(x)在 ( a , b ) (a,b) (a,b)上每一点可导,在 x = a x=a x=a有右导数,在 x = b x=b x=b有左导数,则称 f ( x ) f(x) f(x)在 [ a , b ] [a,b] [a,b]上可导。
【注】椭圆 x 2 a 2 + y 2 b 2 = 1 ⇒ y = b a a 2 − x 2 , x ∈ [ − a , a ] , y \frac{x^2}{a^2}+\frac{y^2}{b^2}=1\Rightarrow y =\frac{b}{a}\sqrt{a^2-x^2},x\in[-a,a],y a2x2+b2y2=1⇒y=aba2−x2,x∈[−a,a],y在 ( − a , a ) (-a,a) (−a,a)上可导, y ′ = − b a ⋅ x a 2 − x 2 , x ∈ ( − a , a ) y'=-\frac{b}{a}\cdot\frac{x}{\sqrt{a^2-x^2}},x\in(-a,a) y′=−ab⋅a2−x2x,x∈(−a,a),当 x = ± a x=\pm a x=±a时, y y y不可导(算导数的极限是无穷大,一个是正无穷大,一个是负无穷大),但不是说明函数在这点没切线,其切线斜率是无穷大,它是垂直于 x x x轴的切线,但是左右导数不相等,说明 y y y在此点没有切线。
相关文章:

【数学分析笔记】第4章第2节 导数的意义和性质(2)
4. 微分 4.2 导数的意义与性质 4.2.3 单侧导数 f ′ ( x ) lim Δ x → 0 f ( x Δ x ) − f ( x ) Δ x lim x → x 0 f ( x ) − f ( x 0 ) x − x 0 f(x)\lim\limits_{\Delta x\to 0}\frac{f(x\Delta x)-f(x)}{\Delta x}\lim\limits_{x\to x_0}\frac{f(x)-f(x_0)…...

深度学习:迁移学习
目录 一、迁移学习 1.什么是迁移学习 2.迁移学习的步骤 1、选择预训练的模型和适当的层 2、冻结预训练模型的参数 3、在新数据集上训练新增加的层 4、微调预训练模型的层 5、评估和测试 二、迁移学习实例 1.导入模型 2.冻结模型参数 3.修改参数 4.创建类ÿ…...

Footprint Growthly Quest 工具:赋能 Telegram 社区实现 Web3 飞速增长
作者:Stella L (stellafootprint.network) 在 Web3 的快节奏世界里,社区互动是关键。而众多 Web3 社区之所以能够蓬勃发展,很大程度上得益于 Telegram 平台。正因如此,Footprint Analytics 精心打造了 Growthly —— 一款专为 Tel…...

进入xwindows后挂起键盘鼠标没有响应@FreeBSD
问题: 在升级pkg包后,系统无法进入xfce等xwindows,表现为黑屏和看见鼠标,左上角有一个白字符块,键盘鼠标没有反应,整个系统卡住。但是可以ssh登录,内部的服务一切正常。 表现 处理过程…...

CentOS7.9 snmptrapd更改162端口
端口更改前: 命令: netstat -an |grep 162 [root@kibana snmp]# netstat -an | grep 162 udp 0 0 0.0.0.0:162 0.0.0.0:* unix 3 [ ] STREAM CONNECTED 45162 /run/systemd/journal/stdout u…...

模糊测试SFuzz亮相第32届中国国际信息通信展览会
9月25日,被誉为“中国ICT市场的创新基地和风向标”的第32届中国国际信息通信展在北京盛大开幕,本次展会将在为期三天的时间内,为信息通信领域创新成果、尖端技术和产品提供国家级交流平台。开源网安携模糊测试产品及相关解决方案精彩亮相&…...

CMake学习
向大佬lyf学习,先把其8服务器中所授fine 文章目录 前言一、CMakeList.txt 命令1. 最外层CMakeLists1.1 cmake_minimum_required()1.2 project()1.3 set()1.4 add_subdirectory(&…...

书生·浦语大模型全链路开源开放体系
书生浦语大模型全链路开源开放体系 大模型应用生态的发展和繁荣是建立在模型基座强大的通用基础能力之上的。上海AI实验室联合团队研究认为,大模型各项性能提升的基础在于语言建模能力的增强,对于大模型的研究应回归语言建模本质,通过更高质量…...

PHP安装swoole扩展无效,如何将文件上传至Docker容器
目录 过程 操作方式 过程 在没有使用过云服务器以前,Docker这个平台一直都很神秘。在我申请了华为云服务器,并使用WordPress镜像去搭建自己的网站以后,我不得不去把Docker平台弄清楚,原因是我使用的一个主题需要安装swoole扩展,才能够正常启用。而要将swoole.so这个扩展…...

Web3.0 应用项目
Web3.0 是下一代互联网的概念,旨在去中心化、用户拥有数据控制权和通过区块链技术实现信任的网络。Web3.0的应用项目主要集中在区块链、加密货币、去中心化应用 (DApps)、去中心化金融 (DeFi)、NFT(非同质化代币)等领域。以下是一些典型的 We…...
—— 重定向与缓冲区)
Linux 学习笔记(十六)—— 重定向与缓冲区
一、文件重定向 矩阵的下标,也就是文件描述符的分配规则,是从0开始空的最小的文件描述符分配给进程新打开的文件;文件输出重定向的原理是,关掉1(输出),然后打开文件,这个新打开的文…...

828华为云征文|WordPress部署
目录 前言 一、环境准备 二、远程连接 三、WordPress简介 四、WordPress安装 1. 基础环境安装 编辑 2. WordPress下载与解压 3. 创建站点 4. 数据库配置 总结 前言 WordPress 是一个非常流行的开源内容管理系统(Content Management System, CMS…...
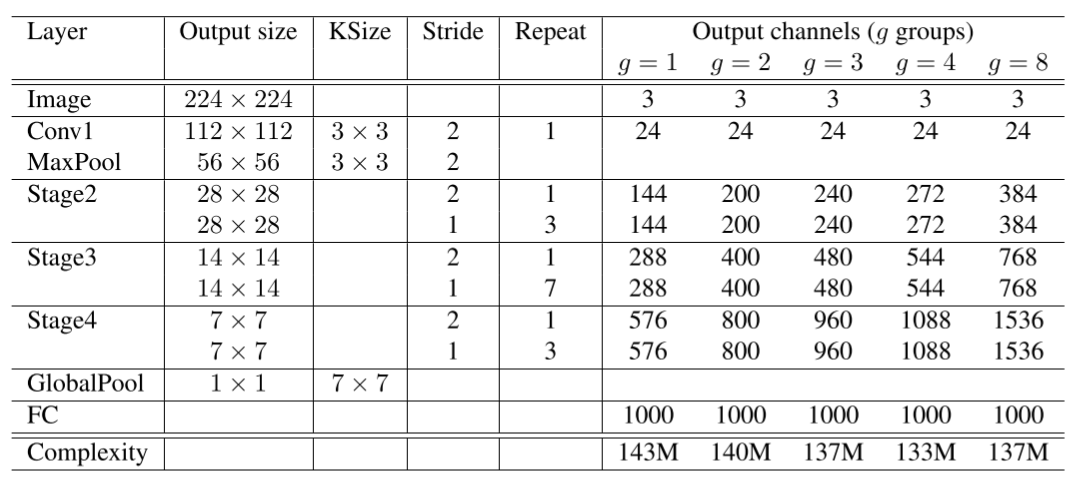
华为开源自研AI框架昇思MindSpore应用案例:计算高效的卷积模型ShuffleNet
如果你对MindSpore感兴趣,可以关注昇思MindSpore社区 ShuffleNet ShuffleNet网络介绍 ShuffleNetV1是旷视科技提出的一种计算高效的CNN模型,和MobileNet, SqueezeNet等一样主要应用在移动端,所以模型的设计目标就是利用有限的计算资源来达到…...

《C++ 小游戏:简易飞机大战游戏的实现》
文章目录 《C 游戏代码解析:简易飞机大战游戏的实现》一、游戏整体结构与功能概述二、各个类和函数的功能分析(一)BK类 - 背景类(二)hero_plane类 - 玩家飞机类(三)plane_bullet类 - 玩家飞机发…...
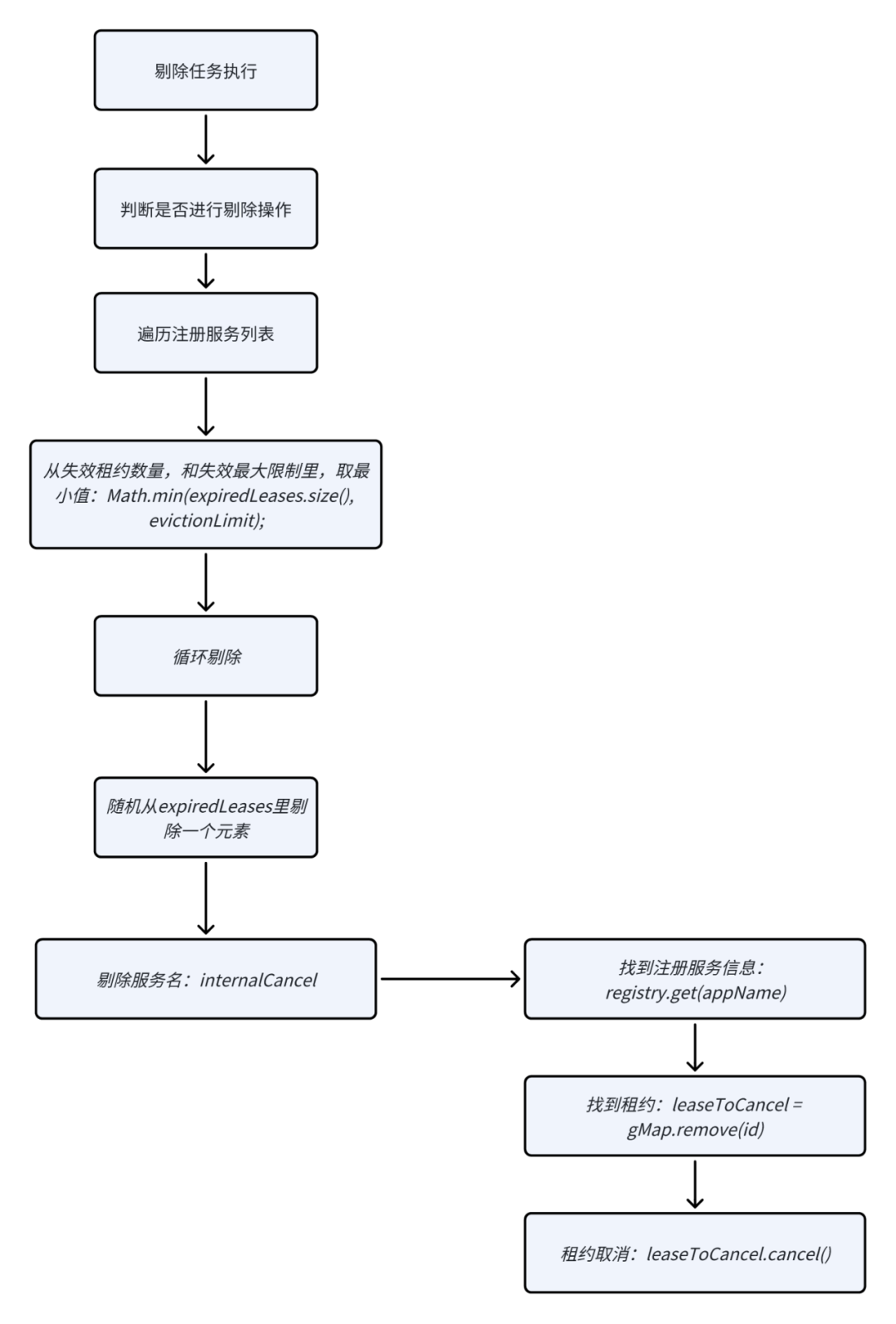
SpringCloud源码:服务端分析(二)- EurekaServer分析
背景 从昨日的两篇文章:SpringCloud源码:客户端分析(一)- SpringBootApplication注解类加载流程、SpringCloud源码:客户端分析(二)- 客户端源码分析。 我们理解了客户端的初始化,其实…...

插槽slot在vue中的使用
介绍 在 Vue.js 中,插槽(slot)是一种用于实现组件内容分发的功能。通过插槽,可以让父组件在使用子组件时自定义子组件内部的内容。插槽提供了一种灵活的方式来组合和复用组件。 项目中有很多地方需要调用一个组件,比…...

针对考研的C语言学习(定制化快速掌握重点2)
1.C语言中字符与字符串的比较方法 在C语言中,单字符可以用进行比较也可以用 > , < ,但是字符串却不能用直接比较,需要用strcmp函数。 strcmp 函数的原型定义在 <string.h> 头文件中,其定义如下: int strcmp(const …...

[C++][IO流][流输入输出][截断理解]详细讲解
目录 1.流输入输出说明1.<<执行顺序2.>>执行顺序 2.截断(trunc)理解 1.流输入输出说明 1.<<执行顺序 链式操作的顺序:当使用多个<<操作符进行链式插入时,执行顺序是从左到右的 每个<<操作都将数据插入到前一个流的输出中…...

阿里云部署1Panel(失败版)
官网脚本部署不成功 这个不怪1panel,这个是阿里Linux 拉不到docker的下载源,懒得思考 正常部署直接打开官网 https://1panel.cn/docs/installation/online_installation/ 但是我使用的阿里云os(Alibaba Cloud Linux 3.2104 LTS 64位) 我执行不管用啊装不上docker 很烦 curl -s…...

九、设备的分配与回收
1.设备分配时应考虑的因素 ①设备的固有属性 设备的固有属性可分为三种:独占设备、共享设备、虚拟设备。 独占设备 一个时段只能分配给一个进程(如打印机) 共享设备 可同时分配给多个进程使用(如磁盘),各进程往往是宏观上同时共享使用设备而微观上交替使用。 …...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

redis和redission的区别
Redis 和 Redisson 是两个密切相关但又本质不同的技术,它们扮演着完全不同的角色: Redis: 内存数据库/数据结构存储 本质: 它是一个开源的、高性能的、基于内存的 键值存储数据库。它也可以将数据持久化到磁盘。 核心功能: 提供丰…...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...
32单片机——基本定时器
STM32F103有众多的定时器,其中包括2个基本定时器(TIM6和TIM7)、4个通用定时器(TIM2~TIM5)、2个高级控制定时器(TIM1和TIM8),这些定时器彼此完全独立,不共享任何资源 1、定…...

数据库正常,但后端收不到数据原因及解决
从代码和日志来看,后端SQL查询确实返回了数据,但最终user对象却为null。这表明查询结果没有正确映射到User对象上。 在前后端分离,并且ai辅助开发的时候,很容易出现前后端变量名不一致情况,还不报错,只是单…...
