矩阵的特征值和特征向量
矩阵的特征值和特征向量是线性代数中非常重要的概念,用于描述矩阵对向量的作用,特别是在矩阵对向量的线性变换中的表现。它们帮助我们理解矩阵在某些方向上的缩放或旋转效果。
1. 特征值和特征向量的定义:
给定一个 n × n n \times n n×n 的方阵 A A A,如果存在一个非零向量 v v v 和一个标量 λ \lambda λ,使得:
A v = λ v A v = \lambda v Av=λv
那么:
- λ \lambda λ 被称为矩阵 A A A 的特征值。
- v v v 被称为对应于特征值 λ \lambda λ 的特征向量。
这意味着,当矩阵 A A A 作用于向量 v v v 时,向量的方向不变,只是被缩放了,缩放因子就是特征值 λ \lambda λ。
2. 特征值和特征向量的几何意义:
-
特征向量 v v v 表示在矩阵变换 A A A 作用下保持方向不变的向量。换句话说,矩阵 A A A 对这个向量的作用仅仅是改变其长度(缩放),而不会改变其方向。
-
特征值 λ \lambda λ 表示矩阵 A A A 作用在特征向量 v v v 上时的缩放因子。如果 λ > 1 \lambda > 1 λ>1,则矩阵 A A A 拉伸特征向量;如果 0 < λ < 1 0 < \lambda < 1 0<λ<1,则矩阵 A A A 压缩特征向量;如果 λ = 0 \lambda = 0 λ=0,则向量被映射为零向量;如果 λ < 0 \lambda < 0 λ<0,则向量被反转方向并缩放。
3. 特征值和特征向量的求法:
为了找到矩阵 A A A 的特征值和特征向量,步骤如下:
(1) 求特征值:
我们要求解特征方程:
A v = λ v A v = \lambda v Av=λv
将其变形为:
( A − λ I ) v = 0 (A - \lambda I)v = 0 (A−λI)v=0
其中 I I I 是单位矩阵, λ \lambda λ 是标量。为了使 v v v 有非零解,矩阵 A − λ I A - \lambda I A−λI 必须是奇异矩阵,即其行列式为 0:
det ( A − λ I ) = 0 \det(A - \lambda I) = 0 det(A−λI)=0
这个方程称为特征值方程。通过解这个方程,我们可以找到矩阵的特征值 λ \lambda λ。
(2) 求特征向量:
一旦求得特征值 λ \lambda λ,我们可以将其代入到方程 ( A − λ I ) v = 0 (A - \lambda I)v = 0 (A−λI)v=0 中,求解线性方程组来找到对应的特征向量 v v v。
4. 举例说明:
让我们通过一个简单的例子来说明特征值和特征向量的计算过程。
假设我们有一个矩阵 A A A:
A = [ 4 1 2 3 ] A = \begin{bmatrix} 4 & 1 \\ 2 & 3 \end{bmatrix} A=[4213]
(1) 求特征值:
我们需要构造特征值方程 det ( A − λ I ) = 0 \det(A - \lambda I) = 0 det(A−λI)=0:
-
构造 A − λ I A - \lambda I A−λI:
A − λ I = [ 4 1 2 3 ] − λ [ 1 0 0 1 ] = [ 4 − λ 1 2 3 − λ ] A - \lambda I = \begin{bmatrix} 4 & 1 \\ 2 & 3 \end{bmatrix} - \lambda \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} = \begin{bmatrix} 4 - \lambda & 1 \\ 2 & 3 - \lambda \end{bmatrix} A−λI=[4213]−λ[1001]=[4−λ213−λ] -
计算行列式:
det ( A − λ I ) = ( 4 − λ ) ( 3 − λ ) − 2 × 1 = λ 2 − 7 λ + 10 − 2 = λ 2 − 7 λ + 8 \det(A - \lambda I) = (4 - \lambda)(3 - \lambda) - 2 \times 1 = \lambda^2 - 7\lambda + 10 - 2 = \lambda^2 - 7\lambda + 8 det(A−λI)=(4−λ)(3−λ)−2×1=λ2−7λ+10−2=λ2−7λ+8 -
解特征值方程:
λ 2 − 7 λ + 8 = 0 \lambda^2 - 7\lambda + 8 = 0 λ2−7λ+8=0使用二次方程公式 λ = − b ± b 2 − 4 a c 2 a \lambda = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} λ=2a−b±b2−4ac,我们可以得到两个特征值:
λ 1 = 4 , λ 2 = 3 \lambda_1 = 4, \quad \lambda_2 = 3 λ1=4,λ2=3
(2) 求特征向量:
接下来,代入每个特征值,求解对应的特征向量。
对于 λ 1 = 4 \lambda_1 = 4 λ1=4:
( A − 4 I ) v = 0 (A - 4I)v = 0 (A−4I)v=0
即:
[ 0 1 2 − 1 ] [ v 1 v 2 ] = [ 0 0 ] \begin{bmatrix} 0 & 1 \\ 2 & -1 \end{bmatrix} \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix} [021−1][v1v2]=[00]
从第一个方程可以得出 v 2 = 0 v_2 = 0 v2=0,第二个方程得出 2 v 1 = 0 2v_1 = 0 2v1=0,所以 v 1 = 1 v_1 = 1 v1=1。因此,特征向量为:
v 1 = [ 1 0 ] v_1 = \begin{bmatrix} 1 \\ 0 \end{bmatrix} v1=[10]
同理,对于 λ 2 = 3 \lambda_2 = 3 λ2=3:
( A − 3 I ) v = 0 (A - 3I)v = 0 (A−3I)v=0
我们可以得到对应的特征向量:
v 2 = [ 1 1 ] v_2 = \begin{bmatrix} 1 \\ 1 \end{bmatrix} v2=[11]
因此,矩阵 A A A 的特征值为 4 4 4 和 3 3 3,对应的特征向量分别为 [ 1 0 ] \begin{bmatrix} 1 \\ 0 \end{bmatrix} [10] 和 [ 1 1 ] \begin{bmatrix} 1 \\ 1 \end{bmatrix} [11]。
5. 特征值和特征向量的性质:
-
特征值的个数:
一个 n × n n \times n n×n 的矩阵最多有 n n n 个特征值(包括重根)。 -
特征值可以是复数:
如果矩阵是实数矩阵,它的特征值可以是复数,特别是当矩阵是非对称矩阵时。 -
对角化:
如果矩阵有 n n n 个线性无关的特征向量,则可以将矩阵对角化。即找到一个可逆矩阵 P P P 和对角矩阵 D D D,使得:
A = P D P − 1 A = P D P^{-1} A=PDP−1其中 D D D 的对角线元素是矩阵 A A A 的特征值。
6. 特征值和特征向量的应用:
-
主成分分析(PCA):
在 PCA 中,数据协方差矩阵的特征值和特征向量用于识别数据的主要方向,帮助降维。 -
振动分析:
在物理学中,特征值用于描述系统的固有频率。机械系统的刚度矩阵和质量矩阵的特征值对应于系统的振动模式。 -
线性判别分析(LDA):
在机器学习中,LDA 使用协方差矩阵的特征值和特征向量来找到投影方向,从而最大化类间差异,最小化类内差异。 -
动力系统:
在动力系统的稳定性分析中,系统的特征值决定了系统是否会趋于稳定或发散。
总结:
- 特征值和特征向量是描述矩阵变换性质的核心概念。特征值表示矩阵如何在某些特定方向上缩放,而特征向量表示这些方向。
- 通过特征值和特征向量,我们可以分析矩阵的性质,如对角化、主成分分析、振动模式等。
- 它们在数据科学、物理学、机器学习等众多领域中有广泛的应用。
相关文章:

矩阵的特征值和特征向量
矩阵的特征值和特征向量是线性代数中非常重要的概念,用于描述矩阵对向量的作用,特别是在矩阵对向量的线性变换中的表现。它们帮助我们理解矩阵在某些方向上的缩放或旋转效果。 1. 特征值和特征向量的定义: 给定一个 n n n \times n nn 的…...

(11)MATLAB莱斯(Rician)衰落信道仿真2
文章目录 前言一、莱斯衰落信道仿真模型二、仿真代码与结果1.仿真代码2.仿真结果画图 三、后续:四、参考文献: 前言 首先给出莱斯衰落信道仿真模型,该模型由直射路径分量和反射路径分量组成,其中反射路径分量由瑞利衰落信道模型构…...

ComfyUI局部重绘换衣讲解
一、下载插件 ComfyUI-Impact-Pack 下载地址 https://github.com/ltdrdata/ComfyUI-Impact-Pack 主要用到sam Detector去绘制衣服蒙版和高斯模糊蒙版,高斯模糊让蒙版边缘更加柔和 sams模型 放在E:\Comfyui\ComfyUI\models\sams二、换衣思路 文生图或直接上传…...

Android——添加联系人
概述 方式一:使用ContentResolver多次写入,每次写入一个字段 第一步 往手机联系人应用中的raw_contacts表添加一条记录 raw_contacts表 ContentValues values new ContentValues();// 往 raw_contacts 添加联系人记录,并获取添加后的联…...

高级 Java Redis 客户端 有哪些?
高级Java Redis客户端主要包括以下几种: 1. Redisson (https://github.com/redisson/redisson) 特点:Redisson是一个在Redis的基础上实现的Java驻留数据网格(In-Memory Data Grid)。它不仅是一个Redis的J…...
jenkins项目发布基础
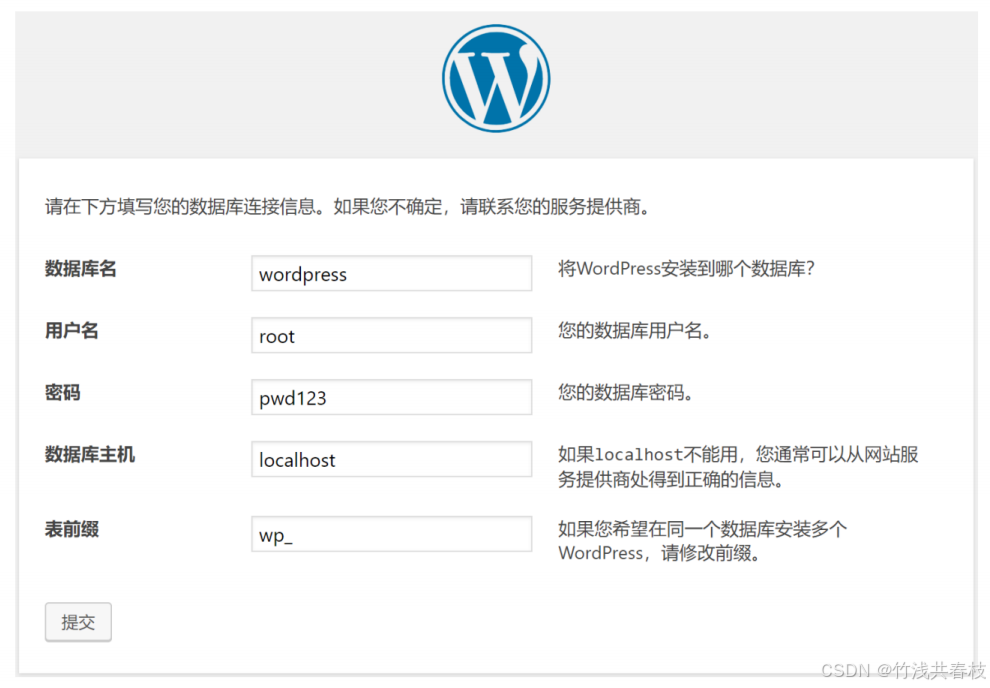
随着软件开发需求及复杂度的不断提高,团队开发成员之间如何更好地协同工作以确保软件开发的质量已经慢慢成为开发过程中不可回避的问题。Jenkins 自动化部署可以解决集成、测试、部署等重复性的工作,工具集成的效率明显高于人工操作;并且持续集成可以更早的获取代码变更的信息,…...

前缀和算法详解
对于查询区间和的问题,可以预处理出来一个前缀和数组 dp,数组中存储的是从下标 0 的位置到当前位置的区间和,这样只需要通过前缀和数组就可以快速的求出指定区间的和了,例如求 l ~ r 区间的和,就可以之间使用 dp[l - 1…...

Android-Handle消息传递和线程通信
本文为作者学习笔记,如有误,请各位大佬指点 目录 一、同步异步 二、Java多线程通信 三、Handler是什么 四、Handler相关的类 五、Handler常用方法 1. 发送消息 2. 接收处理消息 3. 切换线程 六、使用Handler 使用Handler更新UI 使用Handler延…...
)
【Kubernetes】常见面试题汇总(四十七)
目录 106.考虑一种情况,公司希望通过保持最低成本来提高效率和技术运营速度。您如何看待公司将如何实现这一目标? 107.假设一家公司想要修改其部署方法,并希望构建一个可扩展性和响应性更高的平台。您如何看待这家公司能够实现这一目标以满足…...

grafana全家桶-loki promtail收集k8s容器日志
loki是grafana旗下轻量级日志收集工具,为了减少loki对集群的影响,把loki的agent日志收集端promtail部署在k8s集群中,loki server部署在集群外面。这样简单做一个解耦,避免大量读写的应用影响到集群内业务服务。 一、promtail部署…...

HTML5+CSS+JavaScript剪子石头布游戏
HTML5CSSJavaScript剪子石头布游戏 用HTML5CSSJavaScript剪子石头布游戏实现剪子石头布游戏,游戏有成绩计数,人、机输赢情况,及平局情况。 ✂代表剪刀,▉代表石头,▓ 代表布,给出人机双方的出拳情况 游戏…...

Flask-3
文章目录 ORMFlask-SQLAlchemySQLAlchemy中的session对象数据库连接设置常用的SQLAlchemy字段类型常用的SQLAlchemy列约束选项 数据库基本操作模型类定义 数据表操作创建和删除表 数据操作基本查询SQLAlchemy常用的查询过滤器SQLAlchemy常用的查询结果方法多条件查询分页器聚合…...

Redis的基本使用
简介 传统的数据库是 关系数据库,但是Redis是键值对数据库传统的数据库是基于 磁盘存储的,但是Redis是基于 内存存储的 基于内存,读写性能更高内存是不大的,只能存储热点信息 安装 绿色软件,安装即可使用 安装服务 手…...

[241004] Linux 系统中配置文件的区别 | VirtualBox 7.1.2 发布,修复多项问题并提升性能
目录 Linux 系统中 /etc/profile, ~/.bash_profile, ~/.profile, ~/.bashrc 等配置文件的区别一、配置文件类型二、配置文件作用三、交互式登录 Shell 和非登录 Shell交互式登录 shell交互式非登录 shell 四、配置文件加载顺序五、~/.bash_profile 和 ~/.bashrc 的区别 Virtual…...

hbuilderx+uniapp+Android宠物用品商城领养服务系统的设计与实现 微信小程序沙箱支付
目录 项目介绍支持以下技术栈:具体实现截图HBuilderXuniappmysql数据库与主流编程语言java类核心代码部分展示登录的业务流程的顺序是:数据库设计性能分析操作可行性技术可行性系统安全性数据完整性软件测试详细视频演示源码获取方式 项目介绍 顾客 领养…...

SVN 迁移到 GIT,并保留提交记录
1)svn账号与git账号映射 创建 user.txt ,格式如下,user.txt 放置在git base here 所选目录下即可 schacon Scott Chacon <schacongeemail.com> selse Someo Nelse <selsegeemail.com> 为了获得 SVN 使用的作者名字列表…...

【数据结构与算法】LeetCode:堆和快排
文章目录 LeetCode:堆和快排排序数组数组中的第K个最大元素 (Hot 100)前 K 个高频元素(Hot 100)数据流的中位数(Hot 100) LeetCode:堆和快排 排序数组 排序数组 双向切分实现快排…...
文档大师:打造一站式 Word 报告解决方案
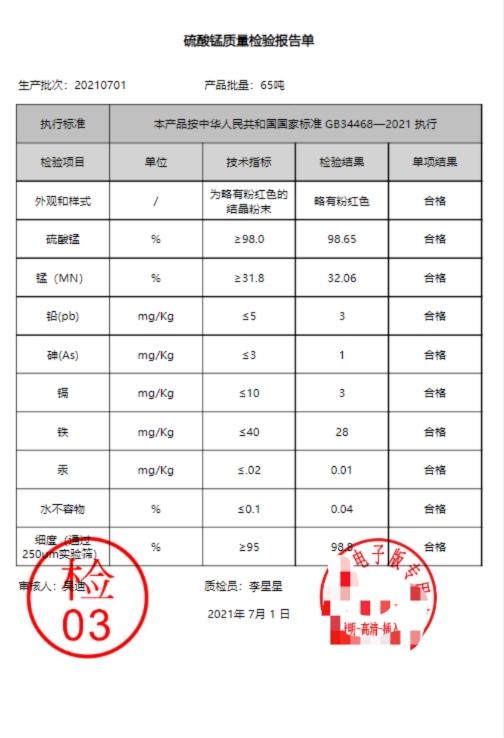
前言 在政府、医院、银行、财务以及销售等领域,常常需要创建各种报告文件来展开工作汇报,譬如季度销售报告、年度总结报告、体检报告和保险合同等。在没有报表工具支持之前,这类报告主要通过 Word 制作,费时费力且难以维护&#…...

Python 数字专题:全方位解析整数
目录 1. 引言 2. 整数的基本概念 2.1 定义 2.2 整数的表示 2.3 创建整数 3. 整数的基本操作 3.1 算术运算 3.2 比较运算 3.3 位运算 4. 内置函数与方法 4.1 int() 函数 4.2 abs() 函数 4.3 pow() 函数 5. 整数的性能优化 5.1 大整数的处理 5.2 使用 numpy 6. 应…...

IP协议报文
一.IP协议报头结构 二.IP协议报头拆解 1.4位版本 实际上只有两个取值,分别是4和6,4代表的是IPv4,6代表的是IPv6。 2.4位首部长度 IP协议报头的长度也是边长的,单位是*4,这里表示的大小为0~15,当数值为1…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

DeepSeek 技术赋能无人农场协同作业:用 AI 重构农田管理 “神经网”
目录 一、引言二、DeepSeek 技术大揭秘2.1 核心架构解析2.2 关键技术剖析 三、智能农业无人农场协同作业现状3.1 发展现状概述3.2 协同作业模式介绍 四、DeepSeek 的 “农场奇妙游”4.1 数据处理与分析4.2 作物生长监测与预测4.3 病虫害防治4.4 农机协同作业调度 五、实际案例大…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...

MySQL JOIN 表过多的优化思路
当 MySQL 查询涉及大量表 JOIN 时,性能会显著下降。以下是优化思路和简易实现方法: 一、核心优化思路 减少 JOIN 数量 数据冗余:添加必要的冗余字段(如订单表直接存储用户名)合并表:将频繁关联的小表合并成…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

elementUI点击浏览table所选行数据查看文档
项目场景: table按照要求特定的数据变成按钮可以点击 解决方案: <el-table-columnprop"mlname"label"名称"align"center"width"180"><template slot-scope"scope"><el-buttonv-if&qu…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...

uniapp 实现腾讯云IM群文件上传下载功能
UniApp 集成腾讯云IM实现群文件上传下载功能全攻略 一、功能背景与技术选型 在团队协作场景中,群文件共享是核心需求之一。本文将介绍如何基于腾讯云IMCOS,在uniapp中实现: 群内文件上传/下载文件元数据管理下载进度追踪跨平台文件预览 二…...

Vue3 PC端 UI组件库我更推荐Naive UI
一、Vue3生态现状与UI库选择的重要性 随着Vue3的稳定发布和Composition API的广泛采用,前端开发者面临着UI组件库的重新选择。一个好的UI库不仅能提升开发效率,还能确保项目的长期可维护性。本文将对比三大主流Vue3 UI库(Naive UI、Element …...
