第十四届蓝桥杯大赛——真题训练第10天
目录
第一题:扫雷
题目描述
输入描述
输出描述
输入输出样例
运行限制
题目代码
第 2 题:完全平方数
问题描述
输入格式
输出格式
样例输入 1
样例输出 1
样例输入 2
样例输出 2
题目分析
题目代码
第三题:求阶乘
问题描述
输入格式
输出格式
样例输入
样例输出
评测用例规模与约定
题目分析
题目代码
第一题:扫雷
题目描述
在一个 n 行 m 列的方格图上有一些位置有地雷,另外一些位置为空。
请为每个空位置标一个整数,表示周围八个相邻的方格中有多少个地雷。
输入描述
输入的第一行包含两个整数 n,m。
第 22 行到第 n+1 行每行包含 m 个整数,相邻整数之间用一个空格分隔。如果对应的整数为 00,表示这一格没有地雷。如果对应的整数为 11,表示这一格有地雷。
其中,1≤n,m≤100 分钟后还是在当天。
输出描述
输出 n 行,每行 m 个整数,相邻整数之间用空格分隔。
对于没有地雷的方格,输出这格周围的地雷数量。对于有地雷的方格,输出 99。
输入输出样例
示例 1
输入
3 4 0 1 0 0 1 0 1 0 0 0 1 0输出
2 9 2 1 9 4 9 2 1 3 9 2运行限制
- 最大运行时间:1s
- 最大运行内存: 128M
题目代码
import java.util.Scanner;public class 扫雷 {public static void main(String[] args) {Scanner sca = new Scanner(System.in);int n = sca.nextInt();int m = sca.nextInt();sca.nextLine();String[][] arr = new String[n][m];for (int i = 0; i < n; i++) {arr[i] = sca.nextLine().split(" ");}for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++) {if (arr[i][j].equals("1")) {System.out.print("9" + " ");} else {int count = 0;//同一行if (j-1>=0&&arr[i][j-1].equals("1")){count++;}if (j+1<m&&arr[i][j+1].equals("1")){count++;}//上一行if (i-1>=0&&arr[i-1][j].equals("1")){count++;}if (i-1>=0&&j-1>=0&&arr[i-1][j-1].equals("1")){count++;}if (i-1>=0&&j+1<m&&arr[i-1][j+1].equals("1")){count++;}//下一行if (i+1<n&&arr[i+1][j].equals("1")){count++;}if (i+1<n&&j-1>=0&&arr[i+1][j-1].equals("1")){count++;}if (i+1<n&&j+1<m&&arr[i+1][j+1].equals("1")){count++;}System.out.print(count+" ");}}System.out.println();}} }
第 2 题:完全平方数
问题描述
一个整数 a 是一个完全平方数, 是指它是某一个整数的平方, 即存在一个 整数 b, 使得 2a=b2 。
给定一个正整数 n, 请找到最小的正整数 x, 使得它们的乘积是一个完全平 方数。
输入格式
输入一行包含一个正整数 n 。
输出格式
输出找到的最小的正整数 x 。
样例输入 1
12
样例输出 1
3
样例输入 2
15
样例输出 2
15
题目分析
(1)找一个x使得x*n为一个平方数
(2)注意数据范围要用long
(3)如何找出这个最小数x呢,如果n是由a*a*b*b.....*y(y为不能开方的数)组成的话
(4)那我们是不是最后只需要把y赋值给x,就可以保证x*n是完全平方数了
参考链接:https://blog.csdn.net/m0_55858611/article/details/129765554
题目代码
import java.util.Scanner;/*** 1、找一个x使得x*n为一个平方数* 2、注意数据类型要用long* 3、如何找出这个最小数x呢,如果n是由a*a*b*b.....*y(y为不能开方的数)组成的话* 4、那我们是不是把x赋值为y,就可以保证n是完全平方数了,其中a、b都是小于等于sqrt(n)的*/ public class 完全平方数 {public static void main(String[] args) {Scanner scan = new Scanner(System.in);long n = scan.nextLong();//正整数nlong res = 0L;//最小正整数for (Long i = 1L; i * i <= n; i++) { // i^2 <= n//如果这个n由(i*i)^k组成,就一直除到它没有i的平方为止if (n % (i * i) == 0) {// n % i^2res = n / (i * i);//每次都维护值是越来越小的}}System.out.print(res);scan.close();} }
第三题:求阶乘
问题描述
满足 N ! 的末尾恰好有 K 个 0 的最小的 N 是多少?
如果这样的 N 不存在输出 −1−1 。
输入格式
一个整数 K 。
输出格式
一个整数代表答案。
样例输入
2样例输出
10评测用例规模与约定
对于 30%30% 的数据, 1≤�≤1061≤K≤106.
对于 100%100% 的数据, 1≤�≤10181≤K≤1018.
题目分析
1)直接算 N! 很难。N! 末尾的 0 取决于1 到 N 中因子 2 和 5的组合个数,实际取决于 5 的个数,因为 5 的倍数个数永远少于 2 的,所以可以统计 1 到 N 中 5 的倍数个数 。
/*
输入一个正整数N,求N!(N的阶乘)末尾有多少个0?
例如
5! = 120,0的个数为1
10! = 3628800,0的个数为2
25! = 15511210043330985984000000,0的个数为6
*//*
算法逻辑:
要判断末尾有几个0就是判断可以整除几次10,
10的因子有5和2,而在0~9之间5的倍数只有一个,2的倍数相对较多,
即转换成了求N阶乘中有几个5的倍数。
*/2)最后用二分来找n
参考原文链接:https://blog.csdn.net/Zhangyanfeng1/article/details/107253252
题目代码
import java.util.Scanner;public class 求阶乘 {public static void main(String[] args) {Scanner sca = new Scanner(System.in);long k = sca.nextLong();long left = 1;long right = (long) 9e18;long res = 0;//二分查找while (left <= right) {long mid = left + (right - left) / 2;if (find_5(mid) < k) {res = mid;left = mid + 1;} else {right = mid - 1;}}if (find_5(res + 1) == k) {System.out.println(res + 1);} else System.out.println(-1);}//为什么要循环除5呢?/*我们举一个例子: n=100时(1) n/5=20;表示在1~n有20个区间大小为5的区间(5只能分解一个5)(2) (n/5)/5=4;表示在1~n有4个区间大小为25的区间(25可以分解两个5)(3)((n/5)/5)/5=0;表示1~n有0个区间大小为125的区间(125可以分解3个5)*/static long find_5(long n) {//找5的倍数的个数long res = 0l;while (n / 5 != 0) {res += n / 5;n = n / 5;}return res;} }
相关文章:

第十四届蓝桥杯大赛——真题训练第10天
目录 第一题:扫雷 题目描述 输入描述 输出描述 输入输出样例 运行限制 题目代码 第 2 题:完全平方数 问题描述 输入格式 输出格式 样例输入 1 样例输出 1 样例输入 2 样例输出 2 题目分析 题目代码 第三题:求阶乘 问题描述…...

3.29~3.30学习总结
刷题情况: 蓝桥杯刷题: Java学习情况: 抽象类:如果将子类中抽取的共性行为(方法),子类的执行不一样的时候 (通俗一点来说,就是无法找到一个万能的方法体供子类使用,但这…...
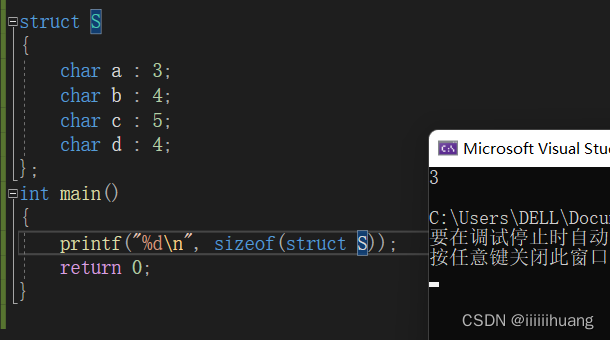
结构体详解 ——— C语言
目录 1.结构体 结构体类型的声明 结构的自引用 结构体变量的定义和初始化 结构体内存对齐 结构体传参 结构体实现位段(位段的填充&可移植性) 位段的内存分配 1.结构体 结构体类型的声明 结构的自引用 结构体变量的定义和初始化 结构体内存对…...
 Java的语言特点)
Java SE 基础(4) Java的语言特点
语言特点 Java是一门面向对象编程语言,不仅吸收了C语言的各种优点,还摒弃了C里难以理解的多继承、指针等概念,因此Java语言具有功能强大和简单易用两个特征。Java语言作为静态面向对象编程语言的代表,极好地实现了面向对象理论&a…...

都炸店了,拼多多还在坚持什么
子超这两天听说了拼多多被“炸店”事件,第一反应是震惊:这都什么年代了,还有这种不择手段的暴力行为?所谓的炸店,就是一些人员被煽动和组织起来,有预谋地对店铺发起打砸行动,这和线下去打砸商铺…...

vue尚品汇商城项目-day01【6.Footer组件的显示与隐藏】
文章目录6.Footer组件的显示与隐藏6.1我们可以根据组件身上的$route获取当前路由的信息,通过路由路径判断Footer显示与隐藏6.2配置路由的时候,可以给路由添加元信息[meta],路由需要配置对象,它的key不能乱接、瞎写、胡写ÿ…...

命令行上的数据科学第二版 一、简介
原文:https://datascienceatthecommandline.com/2e/chapter-1-introduction.html 贡献者:Ting-xin 这本书是关于如何利用命令行做数据科学的。我的目标是通过教你使用命令行的力量,让自己成为一名更高效和多产的数据科学家。 在标题中同时使…...

utf-8转换到utf-16的转换过程你懂吗?
人生自是有情痴,此恨不关风与月。——唐代元稹《离思》 从UTF-8编码的文件中读取文本并将其存储到Java的String对象中,涉及到从字节序列到Unicode码点,再到UTF-16编码的转换。以下是详细的步骤: 从文件读取字节序列:首…...

C++编程大师之路:从入门到精通--持续更新中~
文章目录前言主要内容C基础入门初识C第一个C程序注释变量常量关键字标识符命名规则数据类型整型sizeof关键字实型(浮点型)字符型转义字符字符串型布尔类型 bool数据的输入运算符算术运算符赋值运算符比较运算符逻辑运算符程序流程结构选择结构if语句三目…...

面试阿里软件测试岗,收到offer后我却毫不犹豫拒绝了....
我大学学的是计算机专业,毕业的时候,对于找工作比较迷茫,也不知道当时怎么想的,一头就扎进了一家外包公司,一干就是2年。我想说的是,但凡有点机会,千万别去外包! 在深思熟虑过后&am…...
和pthread_join()的多线程详解)
【c语言多线程编程】关于pthread_create()和pthread_join()的多线程详解
关于pthread_create()和pthread_join()的多线程详解 一、首先说一下pthread_create() 函数的用法: int pthread_create(pthread_t *thread,const pthread_attr_t *attr,void *(*start_routine) (void *),void *arg);各参数的含义: 1、pthread_t *thre…...
抖音seo矩阵系统源码搭建技术+二开开源代码定制部署
抖音已经成为了当今最为流行的短视频平台之一,拥有着庞大的用户群体和海量的视频资源。对于一些商家或者运营者来说,如何从这些视频资源中挖掘出有效的信息,进而提升自己的品牌、产品或者内容的曝光度,就成为了一个非常重要的问题…...

【周赛刷题】平衡树+图中最短环
2612. 最少翻转操作数(平衡树) 题目的难度有一部分在于数学推导。对于某个点 iii 进行反转是有一个范围的,这个范围需要考虑到边界的情况。可以的得到的一个结论是。对于窗口反转,KaTeX parse error: Expected group after ^ at p…...

C++笔记——第十篇 继承 的解析,详细易懂哦
目录 一、继承的概念及定义 1.继承的概念 2. 继承定义 2.1定义格式 2.2继承关系和访问限定符 2.3继承基类成员访问方式的变化 二、基类和派生类对象赋值转换 三、继承中的作用域 四、派生类的默认成员函数 五、继承与友元 六、继承与静态成员 七、复杂的菱形继承…...

SQL Server中的全文搜索
SQL Server中的全文搜索一、概述二、全文搜索查询三、将全文搜索查询与 LIKE 谓词进行比较四、全文搜索体系结构4.1、SQL Server 进程4.2、过滤器守护程序主机进程五、全文搜索处理5.1、全文索引过程5.2、全文查询流程六、全文索引体系结构6.1、全文索引结构6.2、全文索引片段6…...

自适应平移混音方法
一、简介: 自适应平移混音方法是一种常见的音频混音技术,它利用自适应滤波器对不同音频信号进行平移和加权,从而实现混音。 二、该方法的基本步骤如下: 采集和存储需要混音的音频信号。 对其中一个音频信号进行预处理,…...

炼钢厂VR职业技能实训软件,提高员工学习效率和掌握技能速度
炼钢作业是一个高危、高压、高温的行业,在实际操作中需要严格遵守安全规范和操作规程,一旦出现差错可能造成巨大的经济损失和人员伤亡。 利用广州华锐互动开发的炼钢厂VR职业技能实训软件,可以有效帮助员工更好地理解和掌握炼钢作业中的相关…...
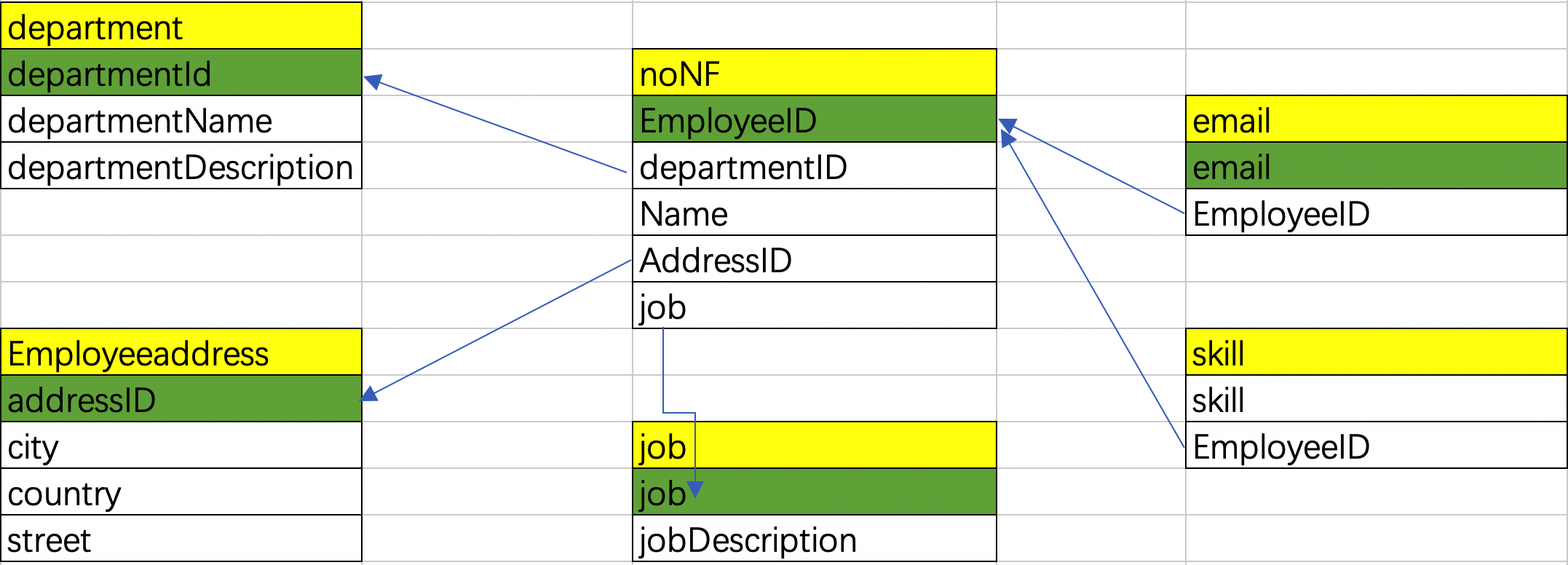
MySQL数据库范式
文章目录MySQL数据库范式1、范式的优缺点2、第一范式3、第二范式4、第三范式5、BC范式6、第四范式MySQL数据库范式 1、范式的优缺点 应用数据库范式的好处: 减少数据冗余(这是最主要的好处,其他好处都是由此而附带的)消除异常&…...

通过多层方法重塑网络安全
多年来,网络安全威胁的复杂性不断增加。此外,随着远程和混合工作场所模式的兴起,网络犯罪分子可以利用的漏洞数量显着增加。由于可能存在的网络威胁的范围如此之广,因此没有一种单一的解决方案可以应对所有威胁。 由于多种原因&a…...
-运算符)
Golang学习+深入(四)-运算符
目录 一、概述 1、算数运算符 2、关系运算符 3、逻辑运算符 4、赋值运算符 5、运算符优先级 6、位运算符 7、其他运算符 二、进制 1、进制转换 1、其他进制转十进制 2、十进制转其他进制 3、二进制转其他进制 4、其他进制转二进制 5、二进制在运算中的说明 三、…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

自然语言处理——Transformer
自然语言处理——Transformer 自注意力机制多头注意力机制Transformer 虽然循环神经网络可以对具有序列特性的数据非常有效,它能挖掘数据中的时序信息以及语义信息,但是它有一个很大的缺陷——很难并行化。 我们可以考虑用CNN来替代RNN,但是…...
