自适应平移混音方法
一、简介:
自适应平移混音方法是一种常见的音频混音技术,它利用自适应滤波器对不同音频信号进行平移和加权,从而实现混音。
二、该方法的基本步骤如下:
采集和存储需要混音的音频信号。
对其中一个音频信号进行预处理,例如滤波或增益调整,以适应混音环境。
对需要混音的所有音频信号进行自适应滤波器处理,得到平移后的信号。
将平移后的信号按照一定比例加权叠加,得到混音后的信号。
根据需要对混音后的信号进行后处理,例如降噪或增益调整。
三、自适应平移混音方法的优点在于,它可以自适应地调整音频信号的平移和加权,以适应不同的混音环境和要求。此外,该方法还可以处理多个音频信号的混音,并且可以通过加权系数来控制混音的平衡。
四、下面是一个自适应平移混音方法的示例代码,我们使用了一个长度为L的自适应滤波器对两个音频信号进行平移处理,得到平移后的信号。其中,自适应滤波器的权重通过迭代方式进行调整。最后,我们将平移后的信号按照一定比例加权叠加,得到混音后的信号。需要注意的是,该示例代码中没有对混音后的信号进行后处理,例如降噪或增益调整,需要根据具体情况进行实现。
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#define N 1024 // number of samples
#define M 2 // number of audio signals
#define L 100 // delay for adaptive filter
float x[N][M]; // audio signals
float y[N]; // filtered signal
float w[L]; // adaptive filter weights
float e[N]; // error signal
float z[N]; // mixed signal
void adaptive_mixing() {
int i, n;
float mu = 0.01; // step size
float sum_x, sum_y, sum_e;
// adaptive filter initialization
for (i = 0; i < L; i++) {
w[i] = 0.0;
}
// adaptive filtering
for (n = L; n < N; n++) {
sum_x = 0.0;
for (i = 0; i < L; i++) {
sum_x += w[i] * x[n-i][1];
}
y[n] = sum_x;
e[n] = x[n][0] - y[n];
for (i = 0; i < L; i++) {
w[i] += mu * e[n] * x[n-i][1];
}
}
// mixing weights
float alpha = 0.7;
float beta = 0.3;
// mixed signal generation
for (n = 0; n < N; n++) {
z[n] = alpha * x[n][0] + beta * y[n];
}
}
相关文章:

自适应平移混音方法
一、简介: 自适应平移混音方法是一种常见的音频混音技术,它利用自适应滤波器对不同音频信号进行平移和加权,从而实现混音。 二、该方法的基本步骤如下: 采集和存储需要混音的音频信号。 对其中一个音频信号进行预处理,…...

炼钢厂VR职业技能实训软件,提高员工学习效率和掌握技能速度
炼钢作业是一个高危、高压、高温的行业,在实际操作中需要严格遵守安全规范和操作规程,一旦出现差错可能造成巨大的经济损失和人员伤亡。 利用广州华锐互动开发的炼钢厂VR职业技能实训软件,可以有效帮助员工更好地理解和掌握炼钢作业中的相关…...
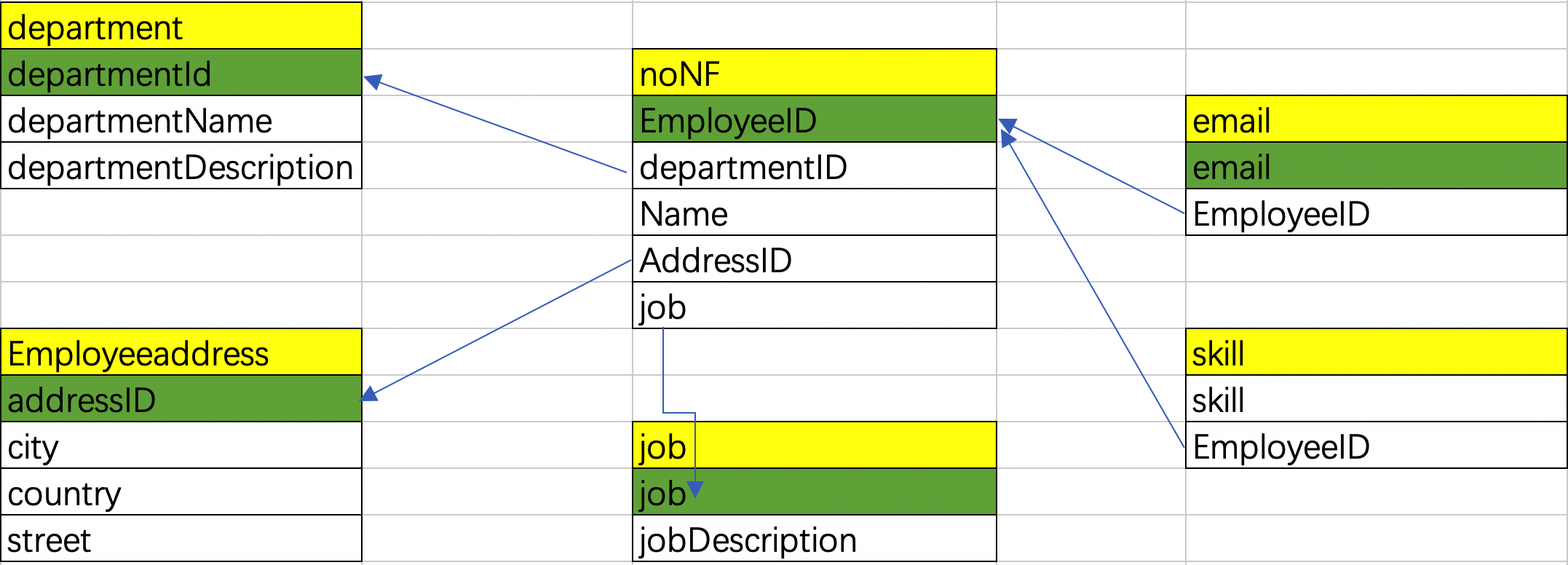
MySQL数据库范式
文章目录MySQL数据库范式1、范式的优缺点2、第一范式3、第二范式4、第三范式5、BC范式6、第四范式MySQL数据库范式 1、范式的优缺点 应用数据库范式的好处: 减少数据冗余(这是最主要的好处,其他好处都是由此而附带的)消除异常&…...

通过多层方法重塑网络安全
多年来,网络安全威胁的复杂性不断增加。此外,随着远程和混合工作场所模式的兴起,网络犯罪分子可以利用的漏洞数量显着增加。由于可能存在的网络威胁的范围如此之广,因此没有一种单一的解决方案可以应对所有威胁。 由于多种原因&a…...
-运算符)
Golang学习+深入(四)-运算符
目录 一、概述 1、算数运算符 2、关系运算符 3、逻辑运算符 4、赋值运算符 5、运算符优先级 6、位运算符 7、其他运算符 二、进制 1、进制转换 1、其他进制转十进制 2、十进制转其他进制 3、二进制转其他进制 4、其他进制转二进制 5、二进制在运算中的说明 三、…...

C++ 运算符重载:C++ 运算符重载的高级技巧和最佳实践
C 运算符重载:深入剖析与实现I. 引言A. 什么是运算符重载B. 为什么要使用运算符重载C. C运算符重载的优缺点II. 运算符重载基本概念A. 运算符重载的定义B. 运算符重载的分类1. 一元运算符2. 二元运算符C. 限制与规范1. 无法重载的运算符2. 重载运算符的规范与建议II…...

软件测试找了2个月了,找不到工作怎么办?
那就问你一些问题,看你能回答多少 1:测试流程是什么?测试用例包含哪些内容?测试用例设计都有哪些?给你一个一次性杯子,你会怎么测试? 2:数据库怎么查看前十行数据?内连接和外连接的区别&#…...

满足高并发的TB API接口接入说明
大家都知道,淘宝的反爬虫机制十分严,而很多时候,没办法高效的拿到数据内容响应终端需求,而依赖爬虫就会造成动不动就出现滑块验证,让人很无解。这里我们分享让采集不再出现任何滑块验证码,完全解密通过&…...

Themis Pro版将正式推出,3次迭代到底在酝酿什么?
最近在社区内讨论火热的Themis Pro,终于要来了!4月2日Themis官网(themis.capital )全新升级改版上线,并宣布Themis Pro 即将于4月下旬正式推出。 Themis Pro 是基于Ve(3,3)模型在FVM公链上搭建的新一代去中…...

边缘检测和轮廓检测
边缘检测 什么是边缘: * 图像中像素值发生剧烈变化的位置(高频信息区域) * 这些区域往往都是图像的边缘 方法:滤波、形态学处理等 边缘的作用 本质上,边缘是不同区域之间的边界。 其中包含了图像的区域信息,形状信息 一方面,可以利用这些信息来作为特征对图像进行理解(甚至…...
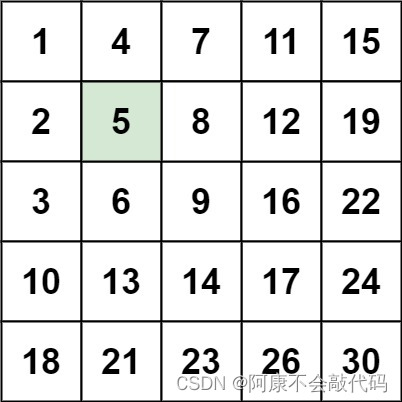
二分法模板以及例题 (三)
167. 两数之和 II - 输入有序数组 输入:numbers [2,7,11,15], target 9 输出:[1,2]。 解释:2 与 7 之和等于目标数 9 。因此 index1 1, index2 2 。返回 [1, 2] 解题思路:首先散列表可以直接秒了,双指针也秒了 二分…...
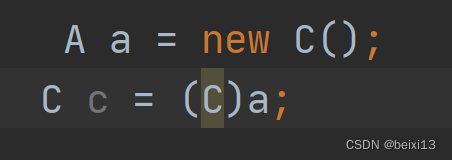
向下转型和向上转型(易理解)
向上转型:父类引用指向子类对象 定义A B C D 四个类,分级继承 对象 a 的编译类型是A,运行类型是B,A是B的父类,父类的引用 a 指向的是B这个子类的对象,因为new的是B这个类,创建的也就是B这个类的…...

华为OD机试用JS实现 -【机智的外卖员】(2023-Q2 押题)
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南华为od机试,独家整理 已参加机试人员的实战技巧本篇题解:机智的外卖员 题目描述: 外…...

同态加密:一个基于多方计算的CKKS方案
这篇文章主要介绍LattiGo团队搞出来的一个多方同态加密的工作。个人觉得比较优雅,而且有库支持,方便把玩,所以记一下。 在攒毕业论文的时候整了这么个看上去很烂,但是(个人觉得)有一点意思的烂活࿰…...
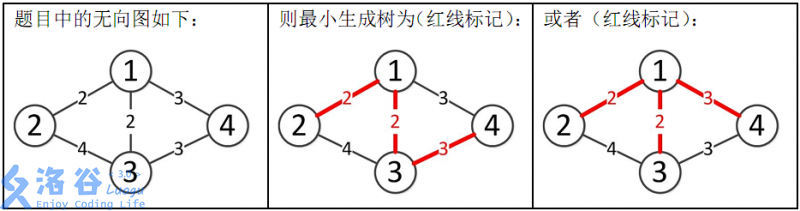
最小生成数
题目描述 如题,给出一个无向图,求出最小生成树,如果该图不连通,则输出 orz。 输入格式 第一行包含两个整数 �,�N,M,表示该图共有 �N 个结点和 �M 条无向边。 接下来 …...
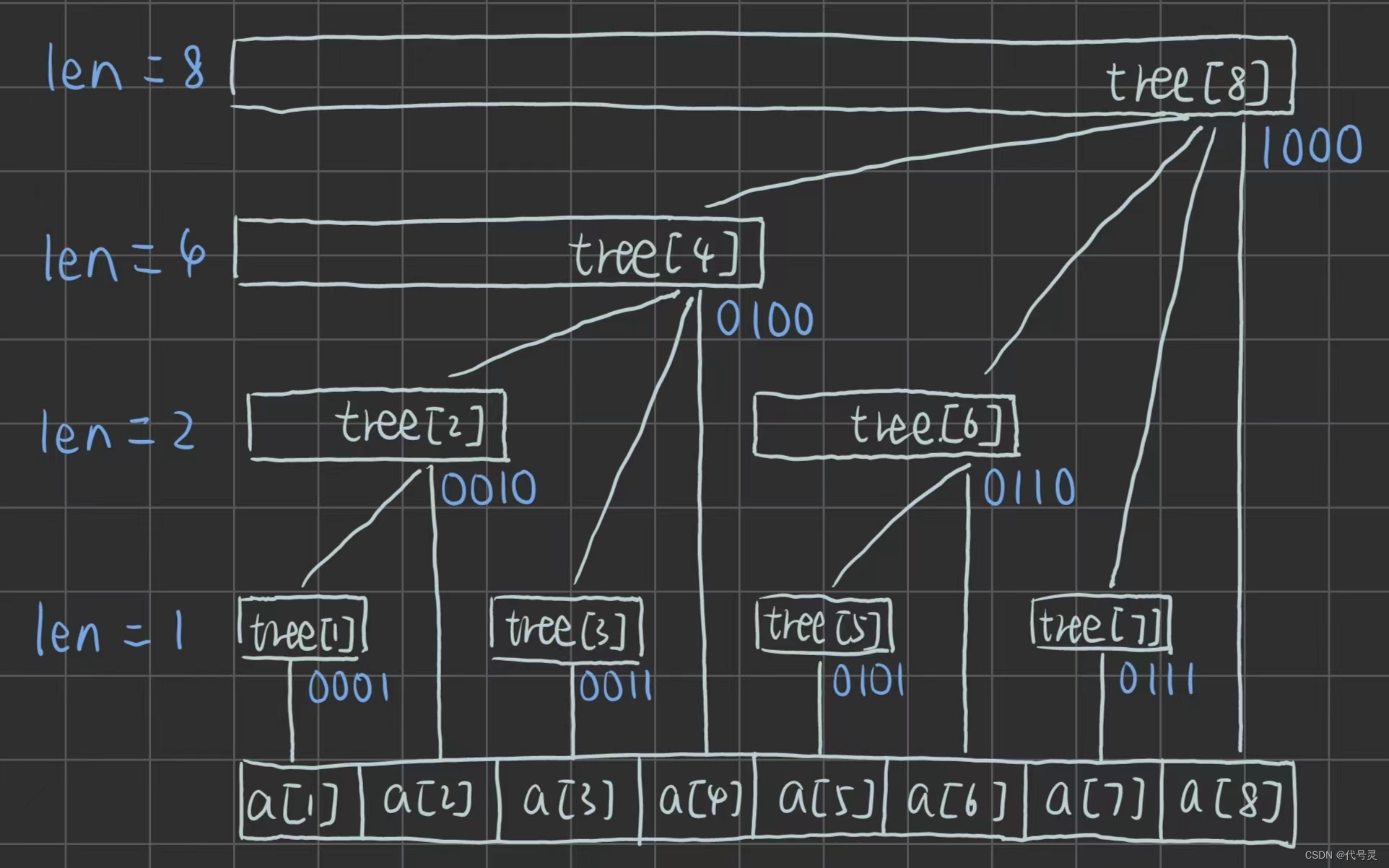
【模板】树状数组
目录: 单点修改,区间查询: 题目描述: lowbit()运算: 插入、修改单点数据: 计算前缀和: 完整代码: 区间修改,单点查询: 计算差分数组: 计算每个点的…...

网站都变成灰色了,怎么实现的?
有些时候我们需要把网站页面变成黑白色或灰色,特别是对于一些需要悼念的日子,以及一些影响力很大的伟人逝世或纪念日的时候,都会让网站的全部网页变成灰色(黑白色),以表示我们对逝者或者英雄的缅怀和悼念。…...
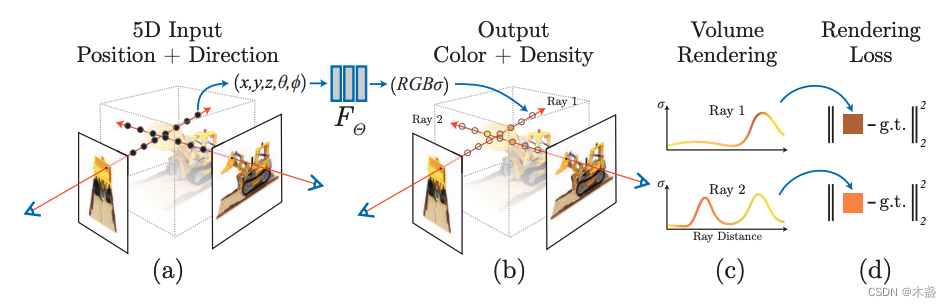
NeRF详解
论文标题:《NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis》 论文地址:https://arxiv.org/abs/2003.08934 推荐代码:https://github.com/yenchenlin/nerf-pytorch 文章目录前言隐式表达NeRF的训练位置编码体渲染&…...

Java之静态代码块和静态类、静态导入
前言 在上一篇文章中给大家讲解了static静态关键字,以及静态变量、静态常量和静态方法等内容。但是关于static,还有其他的一些内容,比如静态类、静态代码块和静态导入等,接下来给大家继续分析讲解。我们一起来看看这些内容都是怎…...

Python3 File isatty() 、os.chflags()方法
Python3 File isatty() 方法Python3 File(文件) 方法概述isatty() 方法检测文件是否连接到一个终端设备,如果是返回 True,否则返回 False。语法isatty() 方法语法如下:fileObject.isatty(); 参数无返回值如果连接到一个终端设备返回 True&…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

SpringCloudGateway 自定义局部过滤器
场景: 将所有请求转化为同一路径请求(方便穿网配置)在请求头内标识原来路径,然后在将请求分发给不同服务 AllToOneGatewayFilterFactory import lombok.Getter; import lombok.Setter; import lombok.extern.slf4j.Slf4j; impor…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...
