【模板】树状数组
目录:
单点修改,区间查询:
题目描述:
lowbit()运算:
插入、修改单点数据:
计算前缀和:
完整代码:
区间修改,单点查询:
计算差分数组:
计算每个点的值:
完整代码:
单点修改,区间查询:
题目描述:
如题,已知一个数列,你需要进行下面两种操作:
-
将某一个数加上 x
-
求出某区间每一个数的和
输入格式
第一行包含两个正整数 n, m,分别表示该数列数字的个数和操作的总个数。
第二行包含 n 个用空格分隔的整数,其中第 i 个数字表示数列第 i 项的初始值。
接下来 m 行每行包含 3 个整数,表示一个操作,具体如下:
-
1 x k含义:将第 x 个数加上 k -
2 x y含义:输出区间 [x, y] 内每个数的和
输出格式
输出包含若干行整数,即为所有操作 2 的结果。
lowbit()运算:
//非负整数n在二进制表示下最低位1及其后面的0构成的数值
//eg.lowbit(12) = lowbit((1100)2) = (100)2 = 4
//将1100按位取反后加一得到0100,会发现除了最低位的一和后面的零,其余位上与原数均相反
//故两者按位与后正好得到最低位1及其后面的0构成的数值
//又取反加一为补码,故lowbit为k & -k
int lowbit(int k) {return k & -k;
}插入、修改单点数据:
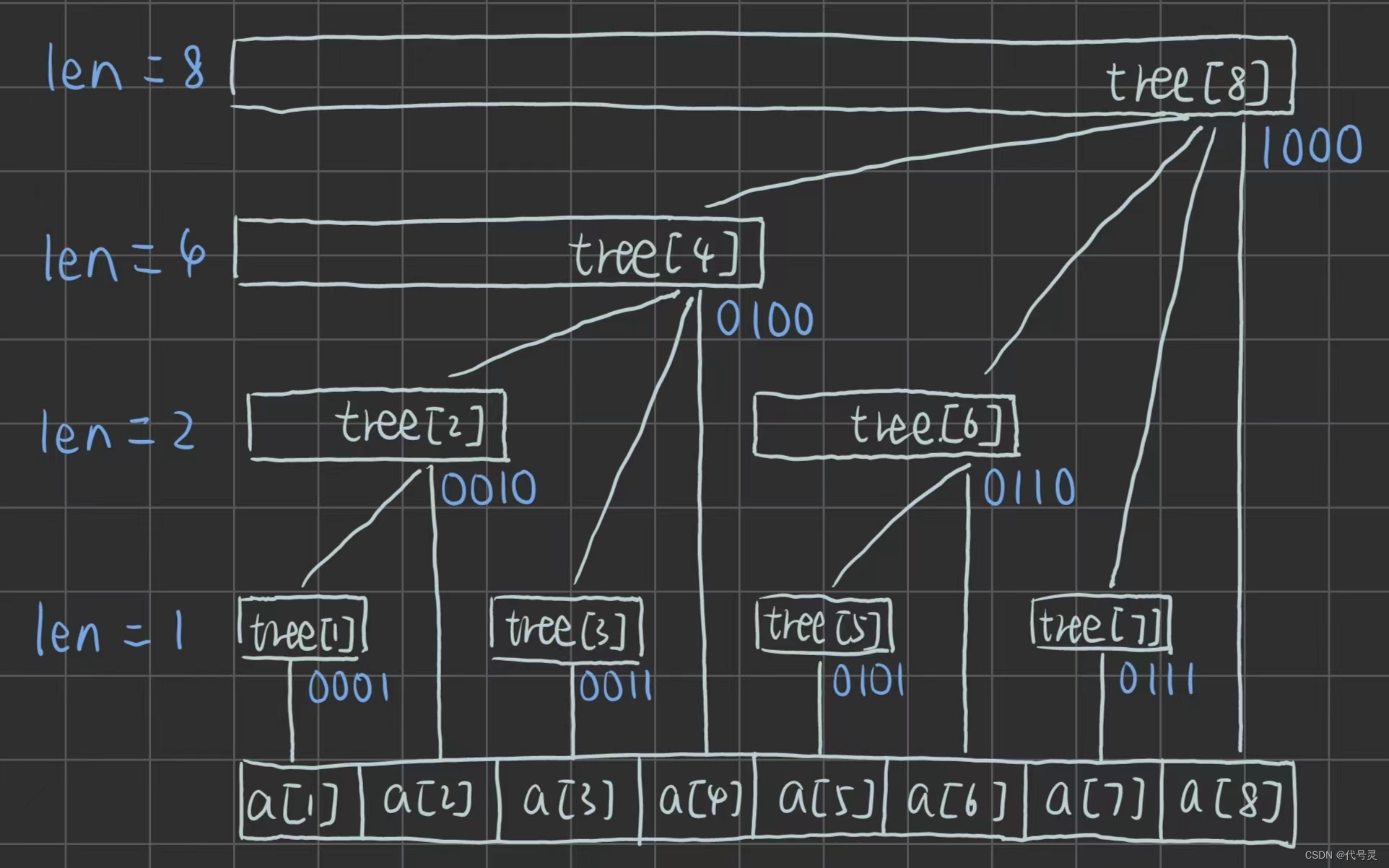
//如图:
//tree[x]保存以x为根的子树中叶节点值的和
//将x转化为二进制后,发现每一层的末尾的零的个数都相同
//且tree[x]覆盖的长度即为lowbit(x)的值
//tree[x]的父节点为tree[x + lowbit(x)]
void add(int x, int k) {while(x <= n) {tree[x] += k;x += lowbit(x);}
}计算前缀和:
//由图可知,若求前7项的和,则该值为tree[7] + tree[6] + tree[4]
//故,通过循环可以求出结果
int sum(int x) {int ans = 0;while(x != 0) {ans += tree[x];x -= lowbit(x);}return ans;
}完整代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 10;
int n, m, a, flag, p, q, tree[N];int lowbit(int k) {return k & -k;
}void add(int x, int k) {while(x <= n) {tree[x] += k;x += lowbit(x);}
}int sum(int x) {int ans = 0;while(x != 0) {ans += tree[x];x -= lowbit(x);}return ans;
}int main() {scanf("%d %d", &n, &m);for(int i = 1; i <= n; ++i) {scanf("%d", &a);add(i, a);}for(int i = 1; i <= m; ++i) {scanf("%d %d %d", &flag, &p, &q);if(flag == 1)add(p, q);elseprintf("%d\n", sum(q) - sum(p - 1));}return 0;
}
区间修改,单点查询:
计算差分数组:
//与单点修改、区间查询类似
void add(int x, int k) {while(x <= n) {tree[x] += k;x += lowbit(x);}
}计算每个点的值:
//与单点修改、区间查询类似
//此时计算的结果为每个点的值
int query(int x) {int ans = 0;while(x != 0) {ans += tree[x];x -= lowbit(x);}return ans;
}完整代码:
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 10;
int n, m, now, last, flag, p, q, num, tree[N];int lowbit(int k) {return k & -k;
}void add(int x, int k) {while(x <= n) {tree[x] += k;x += lowbit(x);}
}int query(int x) {int ans = 0;while(x != 0) {ans += tree[x];x -= lowbit(x);}return ans;
}int main() {scanf("%d %d", &n, &m);//计算差分数组,将相差的值放入数组中//eg.原本的数组应为a[] = {1, 6, 8, 5, 10}//则差分数组应为b[] = {1, 5, 2, -3, 5}for(int i = 1; i <= n; ++i) {scanf("%d", &now);add(i, now - last);last = now;}for(int i = 1; i <= m; ++i) {scanf("%d", &flag);//若要修改区间[p, q]的值//例如上述举的例子,若要将区间[2, 4]均加上3//则原数组变为a[] = {1, 9, 11, 8, 10}//差分数组变为b[] = {1, 8, 2, -3, 2}//即对差分数组来说只需修改下标为p的值,和下标为q + 1的值if(flag == 1) {scanf("%d %d %d", &p, &q, &num);add(p, num);add(q + 1, -num);}//若查询某个点的值//前p个差分数组的值相加即为该点的值//与单点修改、区间查询中的求前缀和类似else {scanf("%d", &p);printf("%d\n", query(p));}}return 0;
}
相关文章:

【模板】树状数组
目录: 单点修改,区间查询: 题目描述: lowbit()运算: 插入、修改单点数据: 计算前缀和: 完整代码: 区间修改,单点查询: 计算差分数组: 计算每个点的…...

网站都变成灰色了,怎么实现的?
有些时候我们需要把网站页面变成黑白色或灰色,特别是对于一些需要悼念的日子,以及一些影响力很大的伟人逝世或纪念日的时候,都会让网站的全部网页变成灰色(黑白色),以表示我们对逝者或者英雄的缅怀和悼念。…...
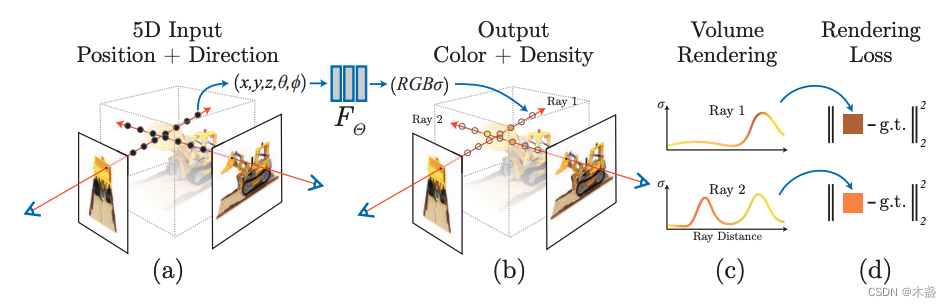
NeRF详解
论文标题:《NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis》 论文地址:https://arxiv.org/abs/2003.08934 推荐代码:https://github.com/yenchenlin/nerf-pytorch 文章目录前言隐式表达NeRF的训练位置编码体渲染&…...

Java之静态代码块和静态类、静态导入
前言 在上一篇文章中给大家讲解了static静态关键字,以及静态变量、静态常量和静态方法等内容。但是关于static,还有其他的一些内容,比如静态类、静态代码块和静态导入等,接下来给大家继续分析讲解。我们一起来看看这些内容都是怎…...

Python3 File isatty() 、os.chflags()方法
Python3 File isatty() 方法Python3 File(文件) 方法概述isatty() 方法检测文件是否连接到一个终端设备,如果是返回 True,否则返回 False。语法isatty() 方法语法如下:fileObject.isatty(); 参数无返回值如果连接到一个终端设备返回 True&…...

【SH_CO_TMT_PACKAGE保留60天数据和增加索引】
1. 保留60天数据 DELETE FROM SH_CO_TMT_PACKAGE WHERE CREATED_ < SYSDATE - 195SH_CO_TMT_PACKAGE 这个表是tmt的数据统计表,数据量极大,大概有1500W 里头的数据都是从TMT机台运行状况表(比如满管率,断丝数,下次落纱时间)同步过来的。 朗通针对这些数据,做了个…...

2022蓝桥杯省赛——数位排序
问题描述 小蓝对一个数的数位之和很感兴趣, 今天他要按照数位之和给数排序。当两个数各个数位之和不同时, 将数位和较小的排在前面, 当数位之和相等时, 将数值小的排在前面。 例如, 2022 排在 409 前面, 因为 2022 的数位之和是 6, 小于 409 的数位之和 13 。 又如, 6 排在 …...
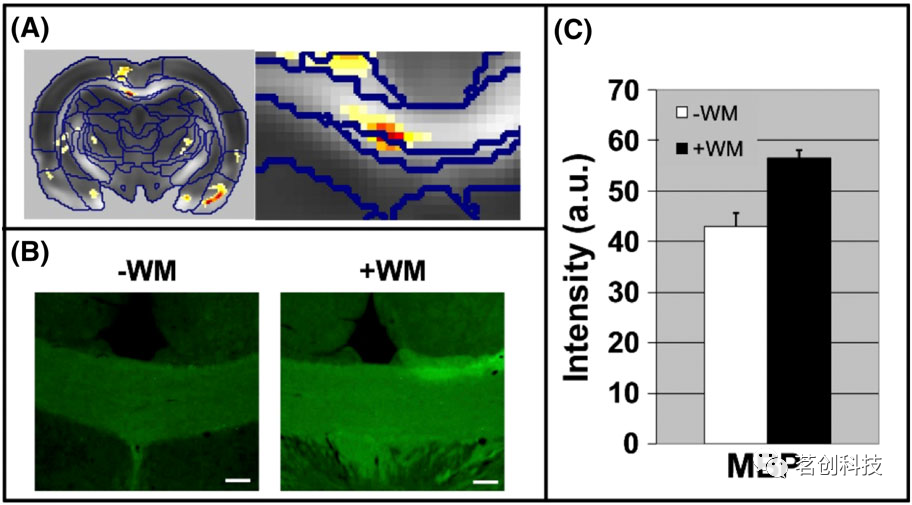
弥散磁共振成像在神经科学中的应用
导读弥散加权成像技术突破了神经科学的界限,使我们能够检查活体人脑的白质微观结构。这为基本的神经科学问题提供了答案,开启了一个以前基本上难以接近的新研究领域。本研究简要总结了神经科学历史上提出的关于大脑白质的关键问题。然后,阐述…...
)
多进程(python)
参考: https://www.liaoxuefeng.com/wiki/1016959663602400/1017627212385376 个人封装的python多进程处理类,跑满CPU,优化性能 概念 进程: 对于操作系统来说,一个任务就是一个进程(Process),…...
利用Kali工具进行信息收集(35)
预备知识 Kali是一款开源的安全漏洞检测工具,是专业用于渗透测试的Linux操作系统,由BackTrack发展而来,可以帮助安全和IT专业人士识别安全性问题,验证漏洞的缓解措施,并管理专家驱动的安全性进行评估,提供真…...

《程序员面试金典(第6版)》 面试题 08.11. 硬币(动态规划,组合问题,C++)
题目描述 硬币。给定数量不限的硬币,币值为25分、10分、5分和1分,编写代码计算n分有几种表示法。(结果可能会很大,你需要将结果模上1000000007) 示例1: 输入: n 5 输出:2 解释: 有两种方式可以凑成总金额: 55 511111 示例2: 输…...
实体商家做抖音运营如何做矩阵?
商家实体门店如何做好短视频矩阵?这是一个值得深入探讨的问题。在当今的数字化时代,短视频成为越来越多企业吸引用户、提高曝光度的一种重要方式,实体店也不例外。在本文中,我们将提供一些实用的建议,帮助实体店如何做…...
java 双列集合Map 万字详解
目录 一、前言 二、概述 三、特点 四、常用方法 1. V put(K key, V value) : Δ代码演示 : 2. V get(Object key) : Δ代码演示 : 3. V remove(Object key) : Δ代码演示 : 4. int size() : Δ代码演示 : 5. default V replace(K key, V value) : Δ代码演示 : 6. bo…...
【数据结构】二叉树<遍历>
【二叉树遍历】|-前序-中序-后序-层序-|<二叉树的遍历>1.前序遍历【递归】2.中序遍历【递归】3.后序遍历【递归】4.层序遍历【非递归】4.1判断是否是完全二叉树<二叉树的遍历> 在学习二叉树遍历之前我们先了解下二叉树的概念。 二叉树是: 1.空树 2.非空…...

linux查看硬件信息
dmidecode用于在linux下获取硬件信息,遵循SMBIOS/DMI标准,可获取包括BIOS、系统、主板、处理器、内存、缓存等等硬件信息 1、查看CPU信息cat /proc/cpuinfo、lscpu 型号:cat /proc/cpuinfo|grep name|cut -f2 -d:|uniq -c 物理核:…...

吐血整理,互联网大厂最常见的 1120 道 Java 面试题(带答案)整理
前言 作为一个 Java 程序员,你平时总是陷在业务开发里,每天噼里啪啦忙敲着代码,上到系统开发,下到 Bug 修改,你感觉自己无所不能。然而偶尔的一次聚会,你听说和自己一起出道的同学早已经年薪 50 万&#x…...
RabbitMQ如何避免消息丢失
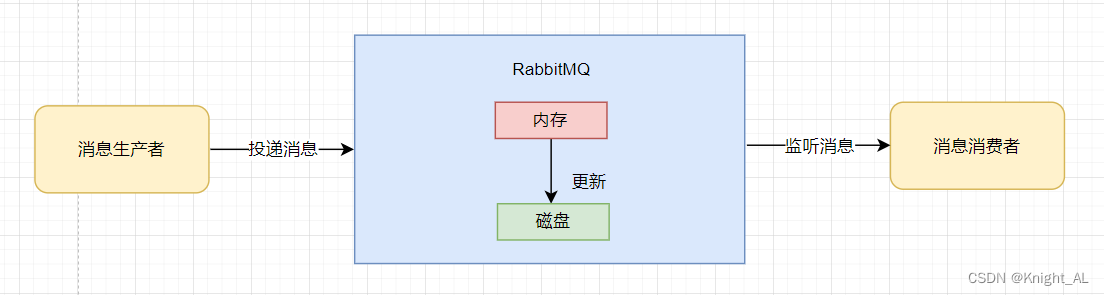
目录1.生产者没有成功把消息发送到MQ2.RabbitMQ接收到消息之后丢失了消息3.消费者弄丢了消息前言 首先明确一点一条消息的传送流程:生产者->MQ->消费者 我们根据这三个依次讨论 1.生产者没有成功把消息发送到MQ 丢失的原因:因为网络传输的不稳定…...
)
做算法题的正确姿势(不断更新)
不停的反思自己,总结建议 做一道算法题,不能去死磕。 如果看一道题,半小时内,没有清晰的思路,就看题解!!!你可能觉得你有点思路,就往里死钻,结果可能就像进…...

p85 CTF夺旗-JAVA考点反编译XXE反序列化
数据来源 图片来源 Java 常考点及出题思路 考点技术:xxe,spel 表达式,反序列化,文件安全,最新框架插件漏洞等 设法间接给出源码或相关配置提示文件,间接性源码或直接源码体现等形式 https://www.cnblog…...

FastJson——JSO字符串与对象的相互转化
一、FastJson介绍 Fastjson是阿里巴巴的开源SON解析库它可以解析JSON格式的字符串,支持将java Bean序列化为ISON字符串,也可以从JSON字符串反序列化到JavaBean。 Fastjson的优点 速度快 fastjson相对其他JSON库的特点是快,从2011年fastj…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...
