NeRF详解
论文标题:《NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis》
论文地址:https://arxiv.org/abs/2003.08934
推荐代码:https://github.com/yenchenlin/nerf-pytorch
文章目录
- 前言
- 隐式表达
- NeRF的训练
- 位置编码
- 体渲染(Volume Rendering)
前言
对于三维重建方向的研究人员来说,NeRF的重要性不言自明。NeRF作为ECCV2022的最佳论文提名之一,是值得精读的经典论文之一。不过,NeRF所涉及的图形学知识过多,对于纯CVer阅读起来较为吃力。本文旨在用朴素易懂的概念来解释NeRF的基本原理。如有不明白之处,欢迎留言交流~
NeRF,全称Neural Radiance Field,即神经辐射场。要了解NeRF,首先要知道NeRF是干嘛的,答:三维场景的新视角合成。NeRF是一种使用神经网络来隐式表达3D场景的技术。
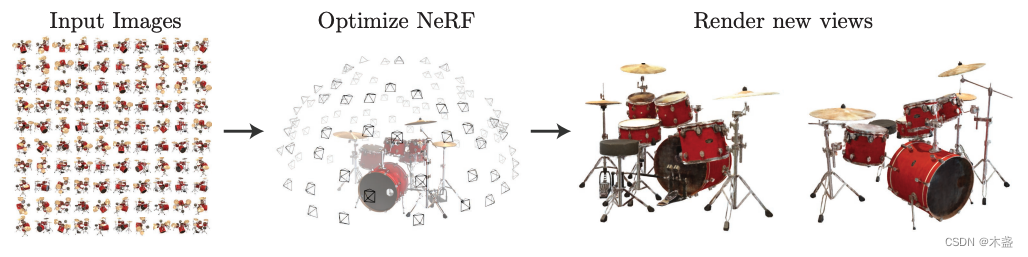
隐式表达
所谓隐式表达,与之相对的就是显式表达。假设我们用NeRF学习了一个确定场景,那么这个场景被隐式地保存在NeRF神经网络的参数中,加入我们需要得到一个新视角的画面,我们需要用神经网络计算出这个画面各个位置的光线和颜色值。
为了更方便理解,我用2D图像表示来举例:
我们有一张2D图像,像素点的坐标是(x,y)(x,y)(x,y),像素点的颜色是(r,g,b)(r,g,b)(r,g,b)。既然坐标和颜色是一一对应的,我们是否可以构建一种映射关系呢?
FΘ(x,y)=(r,g,b)(1)F_{\Theta}(x,y)=(r,g,b)\tag{1}FΘ(x,y)=(r,g,b)(1)
这种映射关系可以被神经网络来表达:
(x,y)→NN→(r,g,b)(2)(x,y)\rightarrow NN \rightarrow (r,g,b)\tag{2}(x,y)→NN→(r,g,b)(2)
我们可以对图像采样一些随机点当作神经网络的训练数据,然后可以用训练好的神经网络来推理这张图像其他位置像素值。这里很好理解,我们直接将这种情况推广到3D,就可以得到NeRF的基本结构。NeRF的公式表达:
FΘ:(x,d)→(c,σ)(3)F_{\Theta}:(\bold{x},\bold{d}) \rightarrow(\bold{c},\sigma)\tag{3}FΘ:(x,d)→(c,σ)(3)
式(3)中的x=(x,y,z)\bold{x}=(x,y,z)x=(x,y,z)表示3D点的坐标,d=(θ,ϕ)\bold{d}=(\theta,\phi)d=(θ,ϕ)表示观测方向,c=(r,g,b)\bold{c}=(r,g,b)c=(r,g,b)表示3D点预测出来的颜色值,σ\sigmaσ表示体密度(一会儿着重解释)。我们对比式(1)和式(3)可以发现一些区别,由平面推广到3D要考虑很多东西,首先一点就是观测角度会影响3D点的颜色表现。所以,整个NeRF的设计就是一套view-dependent的思路,所以NeRF的输入除了3D位置以外,还需要观测角度,一共需要5D向量作为输入,即(x,y,z,θ,ϕ)(x,y,z,\theta,\phi)(x,y,z,θ,ϕ)。输出结果为该3D点的像素值c\bold{c}c和体密度σ\sigmaσ,这两个输出可以用来进行体渲染(volume rendering)。
NeRF的训练
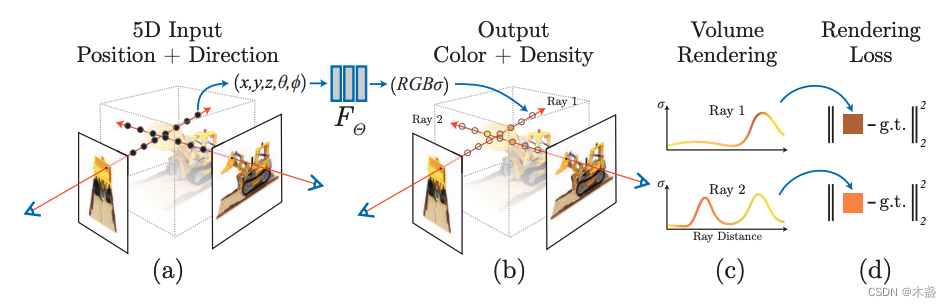
从图2我们可知,NeRF是5D输入(x,y,z,θ,ϕ)(x,y,z,\theta,\phi)(x,y,z,θ,ϕ)和4D输出(r,g,b,σ)(r,g,b,\sigma)(r,g,b,σ)。如子图(a)所示,对于某已知视图,我们可以对每个2D点作出射线,然后沿着射线的方向(即深度方向)做多个点的采样,至于射线原理不太明白请了解一下相机二维坐标和三维坐标的映射关系(《【AI数学】相机成像之内参数》)。
位置编码
γ(p)=(sin(20πp),cos(20πp),⋯,sin(2L−1πp),cos(2L−1πp))(4)\gamma(p)=\left(\sin \left(2^0 \pi p\right), \cos \left(2^0 \pi p\right), \cdots, \sin \left(2^{L-1} \pi p\right), \cos \left(2^{L-1} \pi p\right)\right)\tag{4}γ(p)=(sin(20πp),cos(20πp),⋯,sin(2L−1πp),cos(2L−1πp))(4)
体渲染(Volume Rendering)
C(r)=∫tntfT(t)σ(r(t))c(r(t),d)dt,where T(t)=exp(−∫tntσ(r(s))ds)(5)C(\mathbf{r})=\int_{t_n}^{t_f} T(t) \sigma(\mathbf{r}(t)) \mathbf{c}(\mathbf{r}(t), \mathbf{d}) d t, \text { where } T(t)=\exp \left(-\int_{t_n}^t \sigma(\mathbf{r}(s)) d s\right) \tag{5}C(r)=∫tntfT(t)σ(r(t))c(r(t),d)dt, where T(t)=exp(−∫tntσ(r(s))ds)(5)
∑i=1NTiαici(6)\sum_{i=1}^N T_i \alpha_i c_i\tag{6}i=1∑NTiαici(6)
Ti=∏j=1i−1(1−αj)(8)T_i=\prod_{j=1}^{i-1}\left(1-\alpha_j\right)\tag{8}Ti=j=1∏i−1(1−αj)(8)
αi=1−e−σiδti(9)\alpha_i=1-e^{-\sigma_i \delta t_i}\tag{9}αi=1−e−σiδti(9)
相关文章:

NeRF详解
论文标题:《NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis》 论文地址:https://arxiv.org/abs/2003.08934 推荐代码:https://github.com/yenchenlin/nerf-pytorch 文章目录前言隐式表达NeRF的训练位置编码体渲染&…...

Java之静态代码块和静态类、静态导入
前言 在上一篇文章中给大家讲解了static静态关键字,以及静态变量、静态常量和静态方法等内容。但是关于static,还有其他的一些内容,比如静态类、静态代码块和静态导入等,接下来给大家继续分析讲解。我们一起来看看这些内容都是怎…...

Python3 File isatty() 、os.chflags()方法
Python3 File isatty() 方法Python3 File(文件) 方法概述isatty() 方法检测文件是否连接到一个终端设备,如果是返回 True,否则返回 False。语法isatty() 方法语法如下:fileObject.isatty(); 参数无返回值如果连接到一个终端设备返回 True&…...

【SH_CO_TMT_PACKAGE保留60天数据和增加索引】
1. 保留60天数据 DELETE FROM SH_CO_TMT_PACKAGE WHERE CREATED_ < SYSDATE - 195SH_CO_TMT_PACKAGE 这个表是tmt的数据统计表,数据量极大,大概有1500W 里头的数据都是从TMT机台运行状况表(比如满管率,断丝数,下次落纱时间)同步过来的。 朗通针对这些数据,做了个…...

2022蓝桥杯省赛——数位排序
问题描述 小蓝对一个数的数位之和很感兴趣, 今天他要按照数位之和给数排序。当两个数各个数位之和不同时, 将数位和较小的排在前面, 当数位之和相等时, 将数值小的排在前面。 例如, 2022 排在 409 前面, 因为 2022 的数位之和是 6, 小于 409 的数位之和 13 。 又如, 6 排在 …...
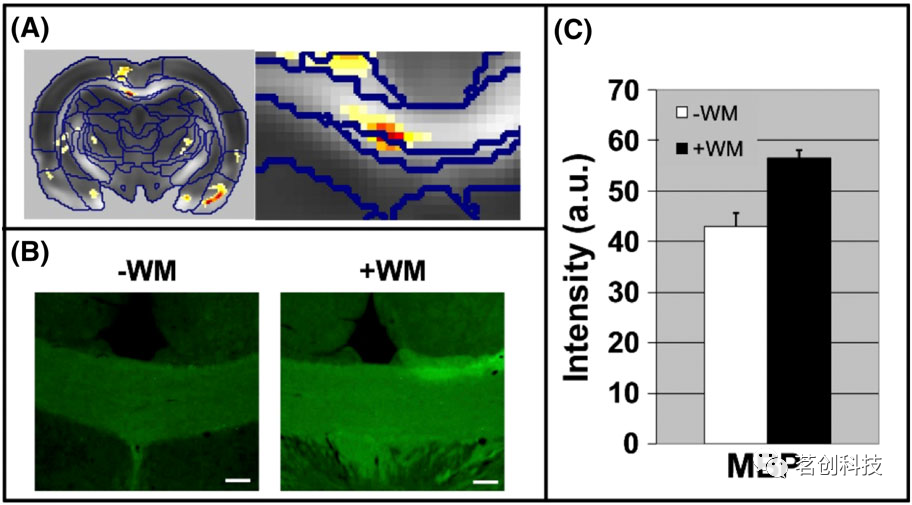
弥散磁共振成像在神经科学中的应用
导读弥散加权成像技术突破了神经科学的界限,使我们能够检查活体人脑的白质微观结构。这为基本的神经科学问题提供了答案,开启了一个以前基本上难以接近的新研究领域。本研究简要总结了神经科学历史上提出的关于大脑白质的关键问题。然后,阐述…...
)
多进程(python)
参考: https://www.liaoxuefeng.com/wiki/1016959663602400/1017627212385376 个人封装的python多进程处理类,跑满CPU,优化性能 概念 进程: 对于操作系统来说,一个任务就是一个进程(Process),…...
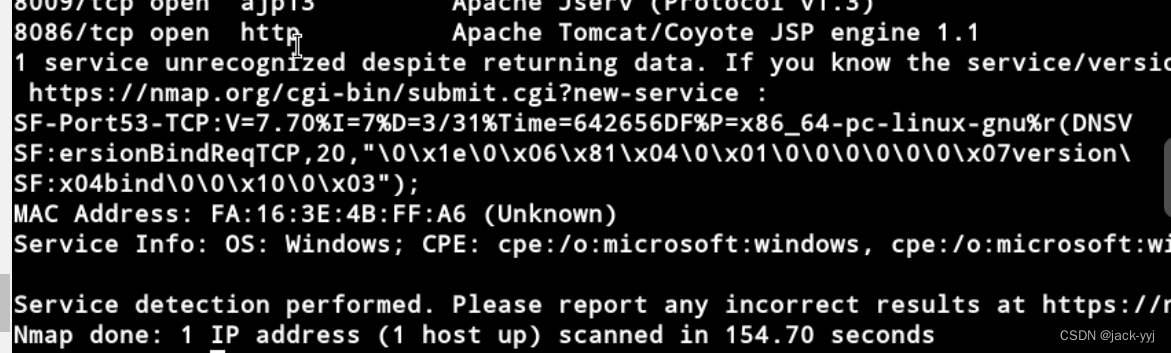
利用Kali工具进行信息收集(35)
预备知识 Kali是一款开源的安全漏洞检测工具,是专业用于渗透测试的Linux操作系统,由BackTrack发展而来,可以帮助安全和IT专业人士识别安全性问题,验证漏洞的缓解措施,并管理专家驱动的安全性进行评估,提供真…...

《程序员面试金典(第6版)》 面试题 08.11. 硬币(动态规划,组合问题,C++)
题目描述 硬币。给定数量不限的硬币,币值为25分、10分、5分和1分,编写代码计算n分有几种表示法。(结果可能会很大,你需要将结果模上1000000007) 示例1: 输入: n 5 输出:2 解释: 有两种方式可以凑成总金额: 55 511111 示例2: 输…...
实体商家做抖音运营如何做矩阵?
商家实体门店如何做好短视频矩阵?这是一个值得深入探讨的问题。在当今的数字化时代,短视频成为越来越多企业吸引用户、提高曝光度的一种重要方式,实体店也不例外。在本文中,我们将提供一些实用的建议,帮助实体店如何做…...
java 双列集合Map 万字详解
目录 一、前言 二、概述 三、特点 四、常用方法 1. V put(K key, V value) : Δ代码演示 : 2. V get(Object key) : Δ代码演示 : 3. V remove(Object key) : Δ代码演示 : 4. int size() : Δ代码演示 : 5. default V replace(K key, V value) : Δ代码演示 : 6. bo…...
【数据结构】二叉树<遍历>
【二叉树遍历】|-前序-中序-后序-层序-|<二叉树的遍历>1.前序遍历【递归】2.中序遍历【递归】3.后序遍历【递归】4.层序遍历【非递归】4.1判断是否是完全二叉树<二叉树的遍历> 在学习二叉树遍历之前我们先了解下二叉树的概念。 二叉树是: 1.空树 2.非空…...

linux查看硬件信息
dmidecode用于在linux下获取硬件信息,遵循SMBIOS/DMI标准,可获取包括BIOS、系统、主板、处理器、内存、缓存等等硬件信息 1、查看CPU信息cat /proc/cpuinfo、lscpu 型号:cat /proc/cpuinfo|grep name|cut -f2 -d:|uniq -c 物理核:…...

吐血整理,互联网大厂最常见的 1120 道 Java 面试题(带答案)整理
前言 作为一个 Java 程序员,你平时总是陷在业务开发里,每天噼里啪啦忙敲着代码,上到系统开发,下到 Bug 修改,你感觉自己无所不能。然而偶尔的一次聚会,你听说和自己一起出道的同学早已经年薪 50 万&#x…...
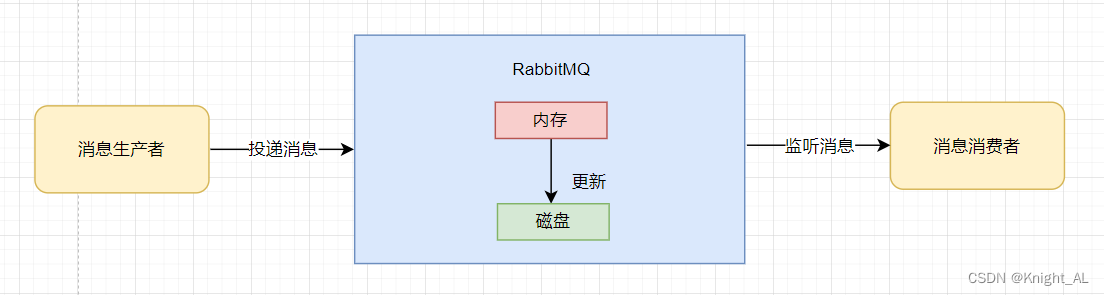
RabbitMQ如何避免消息丢失
目录1.生产者没有成功把消息发送到MQ2.RabbitMQ接收到消息之后丢失了消息3.消费者弄丢了消息前言 首先明确一点一条消息的传送流程:生产者->MQ->消费者 我们根据这三个依次讨论 1.生产者没有成功把消息发送到MQ 丢失的原因:因为网络传输的不稳定…...
)
做算法题的正确姿势(不断更新)
不停的反思自己,总结建议 做一道算法题,不能去死磕。 如果看一道题,半小时内,没有清晰的思路,就看题解!!!你可能觉得你有点思路,就往里死钻,结果可能就像进…...

p85 CTF夺旗-JAVA考点反编译XXE反序列化
数据来源 图片来源 Java 常考点及出题思路 考点技术:xxe,spel 表达式,反序列化,文件安全,最新框架插件漏洞等 设法间接给出源码或相关配置提示文件,间接性源码或直接源码体现等形式 https://www.cnblog…...

FastJson——JSO字符串与对象的相互转化
一、FastJson介绍 Fastjson是阿里巴巴的开源SON解析库它可以解析JSON格式的字符串,支持将java Bean序列化为ISON字符串,也可以从JSON字符串反序列化到JavaBean。 Fastjson的优点 速度快 fastjson相对其他JSON库的特点是快,从2011年fastj…...
《程序员面试金典(第6版)》面试题 08.08. 有重复字符串的排列组合(回溯算法,全排列问题)C++
题目描述 有重复字符串的排列组合。编写一种方法,计算某字符串的所有排列组合。 示例1: 输入:S “qqe” 输出:[“eqq”,“qeq”,“qqe”] 示例2: 输入:S “ab” 输出:[“ab”, “ba”] 提示: 字符都是英文字母。…...

k8s API限流——server级别整体限流和客户端限流
1. 背景 为了防止突发流量影响apiserver可用性,k8s支持多种限流配置,包括: MaxInFlightLimit,server级别整体限流Client限流EventRateLimit, 限制eventAPF,更细力度的限制配置 1.1 MaxInFlightLimit限流 apiserver…...

接口测试中缓存处理策略
在接口测试中,缓存处理策略是一个关键环节,直接影响测试结果的准确性和可靠性。合理的缓存处理策略能够确保测试环境的一致性,避免因缓存数据导致的测试偏差。以下是接口测试中常见的缓存处理策略及其详细说明: 一、缓存处理的核…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...

加密通信 + 行为分析:运营商行业安全防御体系重构
在数字经济蓬勃发展的时代,运营商作为信息通信网络的核心枢纽,承载着海量用户数据与关键业务传输,其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级,传统安全防护体系逐渐暴露出局限性&a…...
