二分法模板以及例题 (三)
167. 两数之和 II - 输入有序数组
输入:numbers = [2,7,11,15], target = 9
输出:[1,2]。
解释:2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。返回 [1, 2]
解题思路:首先散列表可以直接秒了,双指针也秒了
二分法是这里面性能不好的一种做法nlog(n),得遍历后找,其他两个O(n)
class Solution {
public:vector<int> twoSum(vector<int>& numbers, int target) {for(int i=0, j=numbers.size()-1;i<j;i++){int l =i+1,r =j;int mid;while(l<r){mid = (l+r+1)/2;if(numbers[i]+numbers[mid]>target)r=mid-1;else l=mid;}if(numbers[i]+numbers[l]==target)return {i+1,l+1};}return {};}
};
240. 搜索二维矩阵 II
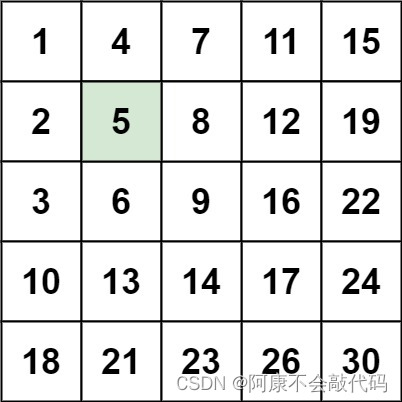
解题思路:双指针秒了,ij从左下角开始,搜索二维矩阵I 是拍平二维数组然后二分,这题应该也是考虑如何拍平
278. 第一个错误的版本
你是产品经理,目前正在带领一个团队开发新的产品。不幸的是,你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的,所以错误的版本之后的所有版本都是错的。
假设你有 n 个版本 [1, 2, …, n],你想找出导致之后所有版本出错的第一个错误的版本。
你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。
这里也可以二分,分从这以后的版本都是错误,从这以前的版本可能正确的,直接使用二分法模板一
// The API isBadVersion is defined for you.
// bool isBadVersion(int version);class Solution {
public:int firstBadVersion(int n) {int left=0;int right=n;int mid=0;while(left<right){mid = (right - left) / 2 + left; if(isBadVersion(mid)){right=mid;}elseleft=mid+1;}return left;}
};
300. 最长递增子序列
输入:nums = [10,9,2,5,3,7,101,18]
输出:4
解释:最长递增子序列是 [2,3,7,101],因此长度为 4 。
class Solution {
public:int lengthOfLIS(vector<int>& nums) { int ans=1;int n=nums.size();vector<int>dp(n,1);for(int i=0;i<n;++i){for(int j=0;j<i;++j){if(nums[i]>nums[j]){dp[i]=max(dp[i],dp[j]+1);if(ans<dp[i])ans=dp[i];}}}return ans;}};
349. 两个数组的交集
输入:nums1 = [1,2,2,1], nums2 = [2,2]
输出:[2]
611. 有效三角形的个数
输入: nums = [2,2,3,4]
输出: 3
解释:有效的组合是:
2,3,4 (使用第一个 2)
2,3,4 (使用第二个 2)
2,2,3
658. 找到 K 个最接近的元素
输入:arr = [1,2,3,4,5], k = 4, x = 3
输出:[1,2,3,4]
相关文章:

二分法模板以及例题 (三)
167. 两数之和 II - 输入有序数组 输入:numbers [2,7,11,15], target 9 输出:[1,2]。 解释:2 与 7 之和等于目标数 9 。因此 index1 1, index2 2 。返回 [1, 2] 解题思路:首先散列表可以直接秒了,双指针也秒了 二分…...
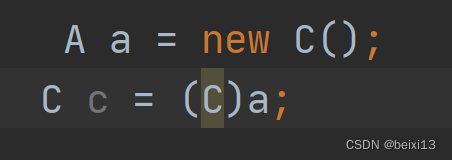
向下转型和向上转型(易理解)
向上转型:父类引用指向子类对象 定义A B C D 四个类,分级继承 对象 a 的编译类型是A,运行类型是B,A是B的父类,父类的引用 a 指向的是B这个子类的对象,因为new的是B这个类,创建的也就是B这个类的…...

华为OD机试用JS实现 -【机智的外卖员】(2023-Q2 押题)
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南华为od机试,独家整理 已参加机试人员的实战技巧本篇题解:机智的外卖员 题目描述: 外…...

同态加密:一个基于多方计算的CKKS方案
这篇文章主要介绍LattiGo团队搞出来的一个多方同态加密的工作。个人觉得比较优雅,而且有库支持,方便把玩,所以记一下。 在攒毕业论文的时候整了这么个看上去很烂,但是(个人觉得)有一点意思的烂活࿰…...
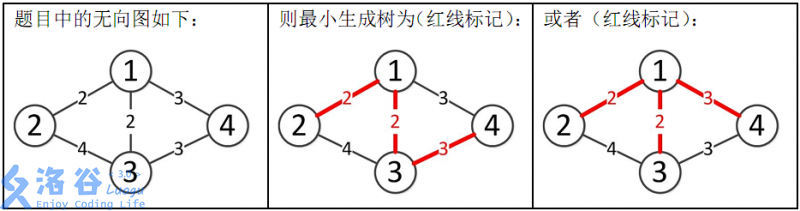
最小生成数
题目描述 如题,给出一个无向图,求出最小生成树,如果该图不连通,则输出 orz。 输入格式 第一行包含两个整数 �,�N,M,表示该图共有 �N 个结点和 �M 条无向边。 接下来 …...
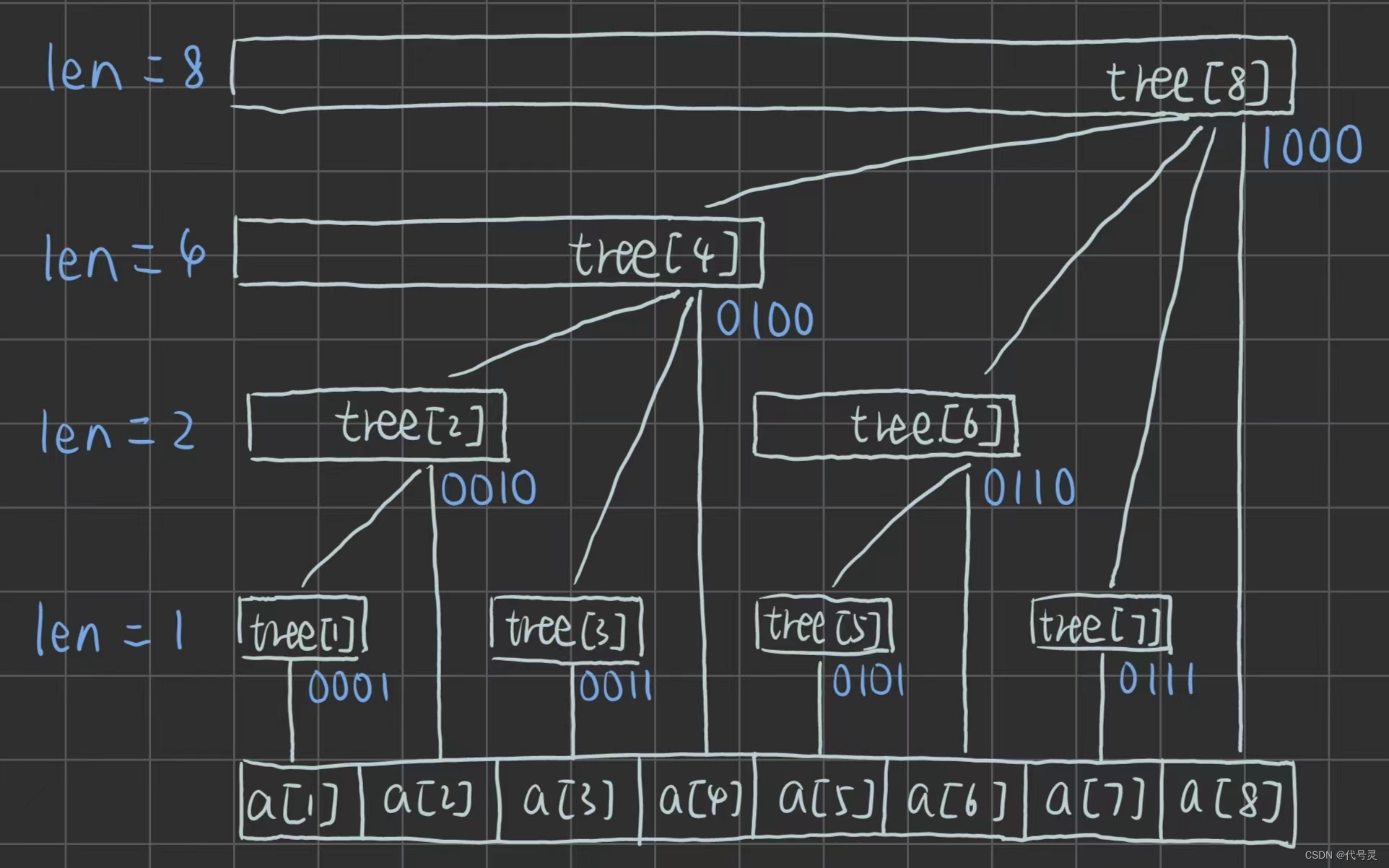
【模板】树状数组
目录: 单点修改,区间查询: 题目描述: lowbit()运算: 插入、修改单点数据: 计算前缀和: 完整代码: 区间修改,单点查询: 计算差分数组: 计算每个点的…...

网站都变成灰色了,怎么实现的?
有些时候我们需要把网站页面变成黑白色或灰色,特别是对于一些需要悼念的日子,以及一些影响力很大的伟人逝世或纪念日的时候,都会让网站的全部网页变成灰色(黑白色),以表示我们对逝者或者英雄的缅怀和悼念。…...
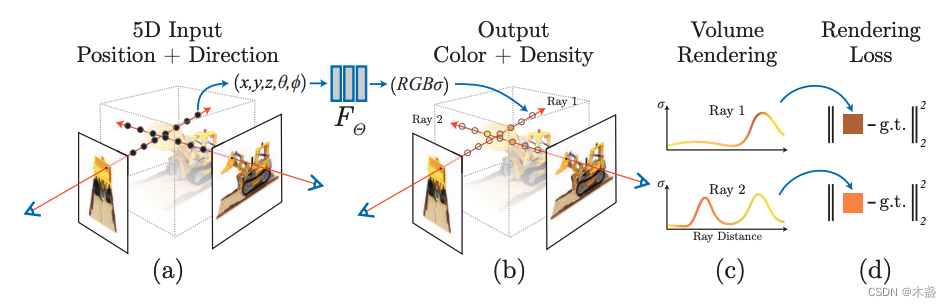
NeRF详解
论文标题:《NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis》 论文地址:https://arxiv.org/abs/2003.08934 推荐代码:https://github.com/yenchenlin/nerf-pytorch 文章目录前言隐式表达NeRF的训练位置编码体渲染&…...

Java之静态代码块和静态类、静态导入
前言 在上一篇文章中给大家讲解了static静态关键字,以及静态变量、静态常量和静态方法等内容。但是关于static,还有其他的一些内容,比如静态类、静态代码块和静态导入等,接下来给大家继续分析讲解。我们一起来看看这些内容都是怎…...

Python3 File isatty() 、os.chflags()方法
Python3 File isatty() 方法Python3 File(文件) 方法概述isatty() 方法检测文件是否连接到一个终端设备,如果是返回 True,否则返回 False。语法isatty() 方法语法如下:fileObject.isatty(); 参数无返回值如果连接到一个终端设备返回 True&…...

【SH_CO_TMT_PACKAGE保留60天数据和增加索引】
1. 保留60天数据 DELETE FROM SH_CO_TMT_PACKAGE WHERE CREATED_ < SYSDATE - 195SH_CO_TMT_PACKAGE 这个表是tmt的数据统计表,数据量极大,大概有1500W 里头的数据都是从TMT机台运行状况表(比如满管率,断丝数,下次落纱时间)同步过来的。 朗通针对这些数据,做了个…...

2022蓝桥杯省赛——数位排序
问题描述 小蓝对一个数的数位之和很感兴趣, 今天他要按照数位之和给数排序。当两个数各个数位之和不同时, 将数位和较小的排在前面, 当数位之和相等时, 将数值小的排在前面。 例如, 2022 排在 409 前面, 因为 2022 的数位之和是 6, 小于 409 的数位之和 13 。 又如, 6 排在 …...
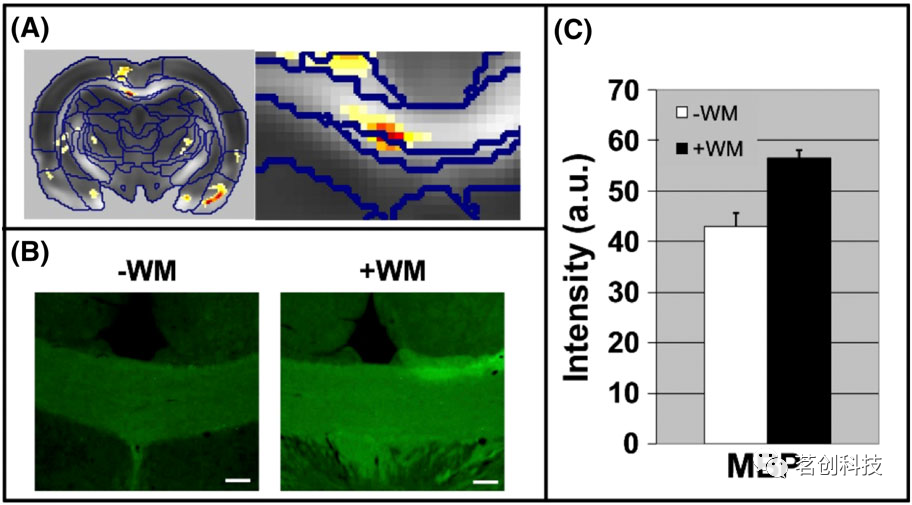
弥散磁共振成像在神经科学中的应用
导读弥散加权成像技术突破了神经科学的界限,使我们能够检查活体人脑的白质微观结构。这为基本的神经科学问题提供了答案,开启了一个以前基本上难以接近的新研究领域。本研究简要总结了神经科学历史上提出的关于大脑白质的关键问题。然后,阐述…...
)
多进程(python)
参考: https://www.liaoxuefeng.com/wiki/1016959663602400/1017627212385376 个人封装的python多进程处理类,跑满CPU,优化性能 概念 进程: 对于操作系统来说,一个任务就是一个进程(Process),…...
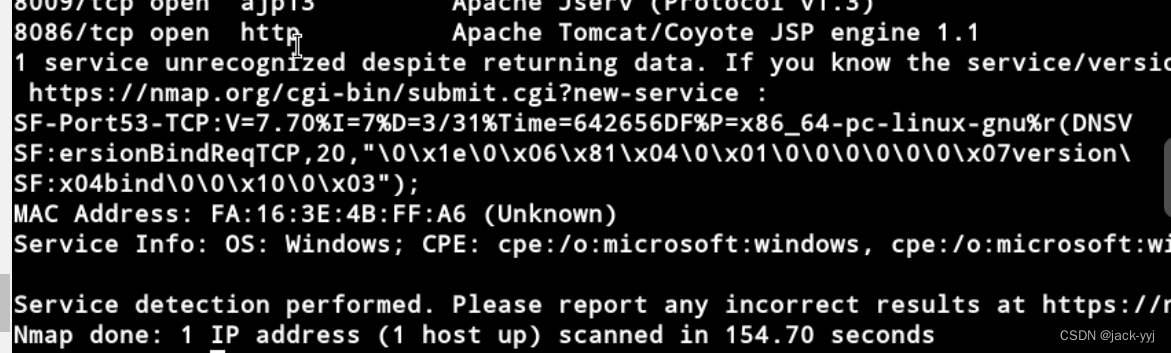
利用Kali工具进行信息收集(35)
预备知识 Kali是一款开源的安全漏洞检测工具,是专业用于渗透测试的Linux操作系统,由BackTrack发展而来,可以帮助安全和IT专业人士识别安全性问题,验证漏洞的缓解措施,并管理专家驱动的安全性进行评估,提供真…...

《程序员面试金典(第6版)》 面试题 08.11. 硬币(动态规划,组合问题,C++)
题目描述 硬币。给定数量不限的硬币,币值为25分、10分、5分和1分,编写代码计算n分有几种表示法。(结果可能会很大,你需要将结果模上1000000007) 示例1: 输入: n 5 输出:2 解释: 有两种方式可以凑成总金额: 55 511111 示例2: 输…...
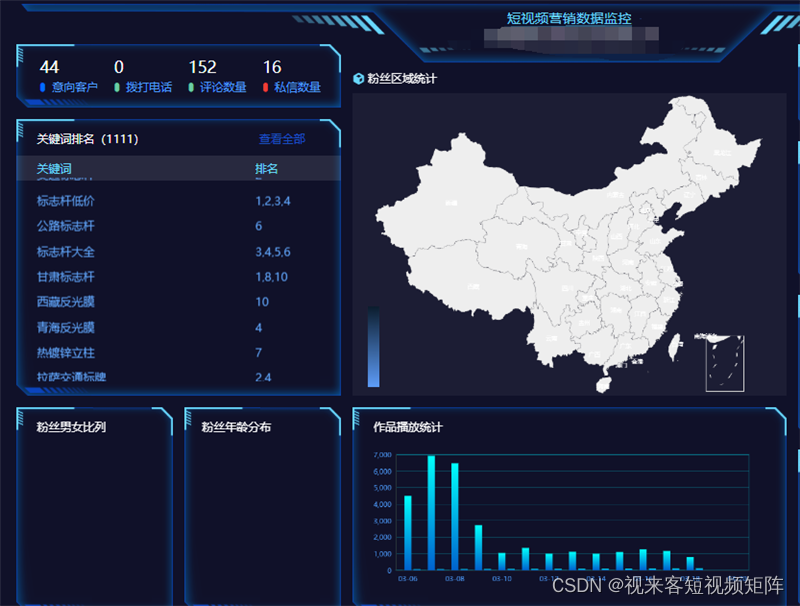
实体商家做抖音运营如何做矩阵?
商家实体门店如何做好短视频矩阵?这是一个值得深入探讨的问题。在当今的数字化时代,短视频成为越来越多企业吸引用户、提高曝光度的一种重要方式,实体店也不例外。在本文中,我们将提供一些实用的建议,帮助实体店如何做…...
java 双列集合Map 万字详解
目录 一、前言 二、概述 三、特点 四、常用方法 1. V put(K key, V value) : Δ代码演示 : 2. V get(Object key) : Δ代码演示 : 3. V remove(Object key) : Δ代码演示 : 4. int size() : Δ代码演示 : 5. default V replace(K key, V value) : Δ代码演示 : 6. bo…...
【数据结构】二叉树<遍历>
【二叉树遍历】|-前序-中序-后序-层序-|<二叉树的遍历>1.前序遍历【递归】2.中序遍历【递归】3.后序遍历【递归】4.层序遍历【非递归】4.1判断是否是完全二叉树<二叉树的遍历> 在学习二叉树遍历之前我们先了解下二叉树的概念。 二叉树是: 1.空树 2.非空…...

linux查看硬件信息
dmidecode用于在linux下获取硬件信息,遵循SMBIOS/DMI标准,可获取包括BIOS、系统、主板、处理器、内存、缓存等等硬件信息 1、查看CPU信息cat /proc/cpuinfo、lscpu 型号:cat /proc/cpuinfo|grep name|cut -f2 -d:|uniq -c 物理核:…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...
相比,优缺点是什么?适用于哪些场景?)
Redis的发布订阅模式与专业的 MQ(如 Kafka, RabbitMQ)相比,优缺点是什么?适用于哪些场景?
Redis 的发布订阅(Pub/Sub)模式与专业的 MQ(Message Queue)如 Kafka、RabbitMQ 进行比较,核心的权衡点在于:简单与速度 vs. 可靠与功能。 下面我们详细展开对比。 Redis Pub/Sub 的核心特点 它是一个发后…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...
