【周赛刷题】平衡树+图中最短环
2612. 最少翻转操作数(平衡树)


题目的难度有一部分在于数学推导。对于某个点 iii 进行反转是有一个范围的,这个范围需要考虑到边界的情况。可以的得到的一个结论是。对于窗口反转,KaTeX parse error: Expected group after '^' at position 4: i+i^̲' = R+L。
并且在c++中可以用到有序set的一些特性的,在实现上是一个红黑树。比如我们可以使用upper_bound() 和 lower_bound()。这两者返回的都是迭代器,其中lower_bound( )函数返回指向第一个大于等于给定值的元素的迭代器, upper_bound( ) 函数返回指向第一个大于给定值的元素的迭代器。
class Solution {
public:vector<int> minReverseOperations(int n, int p, vector<int>& banned, int k) {// [max(k-1-i, i-k+1), min(2n-1-k-i, i+k-1)]set<int> st[2];// 初始化vector<int> ans(n, -1);queue<int> q;q.push(p); ans[p] = 0;unordered_set<int> ban;for (int x:banned){ban.insert(x);ans[x] = -1;}// 考虑到奇偶性,维护两颗平衡树for(int i = 0;i<n;i++){if(i!=p && !ban.count(i)){st[i%2].insert(i);}}while(!q.empty()){int cur = q.front();q.pop();int l = max(k-1-cur, cur-k+1);int r = min(2*n-1-k-cur, cur+k-1);// 如果不加 & 就会复制一份,导致超时// 并不是复制,而至直接拿到引用set<int>& cur_st = st[l%2];auto it = cur_st.lower_bound(l);// 对于迭代器的使用// 1. 首先需要知道lower_bound得到是一个迭代器// 2. 如果得不到合适的,就返回end,因此我们需要判断下// 3. 对于迭代器的取值,需要用*while(it != cur_st.end()){int cur_v = *it;if(cur_v > r) break;ans[cur_v] = ans[cur]+1;q.push(*it);// 对于set常用的函数 insert(), erase()it = cur_st.erase(it);}}return ans;}
};2608. 图中的最短环

这可能是一个模板题目,实现一个最短的环。
基本的思路有两种,都是基于bfs进行操作。一个是删除边,一个是删除点。都是需要枚举起始点。
对于删除边,就对于两个连通的边,我们进行bfs操作。对于起点 iii,我们如果能第二次访问到点 iii,就说明存在环,并且bfs的特性保证一定是第一次最短的。
class Solution {
public:int findShortestCycle(int n, vector<vector<int>>& edges) {// 模板构建双向无权图vector<vector<int>> g(n);for (auto &e: edges){int x = e[0], y = e[1];g[x].push_back(y);g[y].push_back(x);}// 初始化一个数组int dis[n];auto bfs = [&](int i){// 初始化一个数组memset(dis, -1, sizeof(dis));dis[i] = 0;queue<pair<int, int>> q;// emplace 方法构造一个对应的pairq.emplace(i, -1);while(!q.empty()){// 使用auto的方法,自动定位正确的cur和fa的类型auto [cur, fa] = q.front(); q.pop();for (int y: g[cur]){if (dis[y] == -1){dis[y] = dis[cur] + 1;q.emplace(y, cur);}else{if (fa == y) continue;return dis[cur] + dis[y] +1;}}}return INT_MAX;};int ans = INT_MAX;for(int i = 0;i<n;i++){ans = min(ans, bfs(i));}return ans==INT_MAX? -1: ans;}
};
相关文章:

【周赛刷题】平衡树+图中最短环
2612. 最少翻转操作数(平衡树) 题目的难度有一部分在于数学推导。对于某个点 iii 进行反转是有一个范围的,这个范围需要考虑到边界的情况。可以的得到的一个结论是。对于窗口反转,KaTeX parse error: Expected group after ^ at p…...

C++笔记——第十篇 继承 的解析,详细易懂哦
目录 一、继承的概念及定义 1.继承的概念 2. 继承定义 2.1定义格式 2.2继承关系和访问限定符 2.3继承基类成员访问方式的变化 二、基类和派生类对象赋值转换 三、继承中的作用域 四、派生类的默认成员函数 五、继承与友元 六、继承与静态成员 七、复杂的菱形继承…...

SQL Server中的全文搜索
SQL Server中的全文搜索一、概述二、全文搜索查询三、将全文搜索查询与 LIKE 谓词进行比较四、全文搜索体系结构4.1、SQL Server 进程4.2、过滤器守护程序主机进程五、全文搜索处理5.1、全文索引过程5.2、全文查询流程六、全文索引体系结构6.1、全文索引结构6.2、全文索引片段6…...

自适应平移混音方法
一、简介: 自适应平移混音方法是一种常见的音频混音技术,它利用自适应滤波器对不同音频信号进行平移和加权,从而实现混音。 二、该方法的基本步骤如下: 采集和存储需要混音的音频信号。 对其中一个音频信号进行预处理,…...

炼钢厂VR职业技能实训软件,提高员工学习效率和掌握技能速度
炼钢作业是一个高危、高压、高温的行业,在实际操作中需要严格遵守安全规范和操作规程,一旦出现差错可能造成巨大的经济损失和人员伤亡。 利用广州华锐互动开发的炼钢厂VR职业技能实训软件,可以有效帮助员工更好地理解和掌握炼钢作业中的相关…...
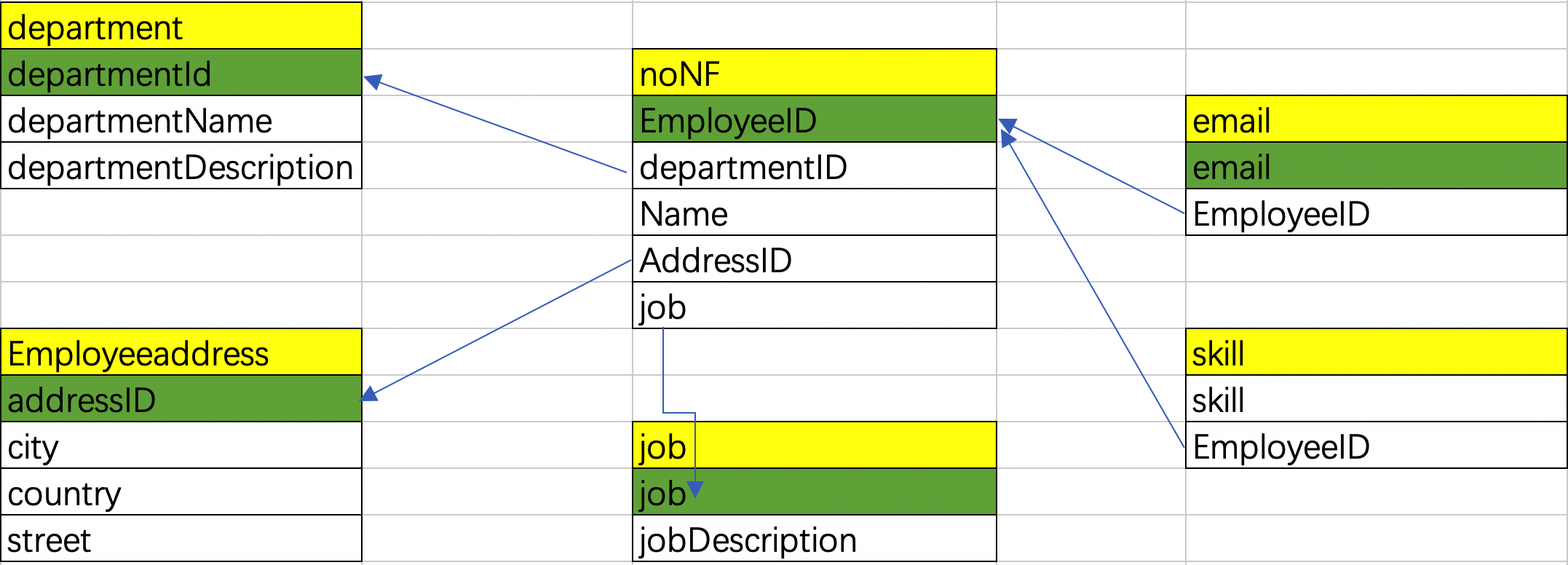
MySQL数据库范式
文章目录MySQL数据库范式1、范式的优缺点2、第一范式3、第二范式4、第三范式5、BC范式6、第四范式MySQL数据库范式 1、范式的优缺点 应用数据库范式的好处: 减少数据冗余(这是最主要的好处,其他好处都是由此而附带的)消除异常&…...

通过多层方法重塑网络安全
多年来,网络安全威胁的复杂性不断增加。此外,随着远程和混合工作场所模式的兴起,网络犯罪分子可以利用的漏洞数量显着增加。由于可能存在的网络威胁的范围如此之广,因此没有一种单一的解决方案可以应对所有威胁。 由于多种原因&a…...
-运算符)
Golang学习+深入(四)-运算符
目录 一、概述 1、算数运算符 2、关系运算符 3、逻辑运算符 4、赋值运算符 5、运算符优先级 6、位运算符 7、其他运算符 二、进制 1、进制转换 1、其他进制转十进制 2、十进制转其他进制 3、二进制转其他进制 4、其他进制转二进制 5、二进制在运算中的说明 三、…...

C++ 运算符重载:C++ 运算符重载的高级技巧和最佳实践
C 运算符重载:深入剖析与实现I. 引言A. 什么是运算符重载B. 为什么要使用运算符重载C. C运算符重载的优缺点II. 运算符重载基本概念A. 运算符重载的定义B. 运算符重载的分类1. 一元运算符2. 二元运算符C. 限制与规范1. 无法重载的运算符2. 重载运算符的规范与建议II…...

软件测试找了2个月了,找不到工作怎么办?
那就问你一些问题,看你能回答多少 1:测试流程是什么?测试用例包含哪些内容?测试用例设计都有哪些?给你一个一次性杯子,你会怎么测试? 2:数据库怎么查看前十行数据?内连接和外连接的区别&#…...

满足高并发的TB API接口接入说明
大家都知道,淘宝的反爬虫机制十分严,而很多时候,没办法高效的拿到数据内容响应终端需求,而依赖爬虫就会造成动不动就出现滑块验证,让人很无解。这里我们分享让采集不再出现任何滑块验证码,完全解密通过&…...

Themis Pro版将正式推出,3次迭代到底在酝酿什么?
最近在社区内讨论火热的Themis Pro,终于要来了!4月2日Themis官网(themis.capital )全新升级改版上线,并宣布Themis Pro 即将于4月下旬正式推出。 Themis Pro 是基于Ve(3,3)模型在FVM公链上搭建的新一代去中…...

边缘检测和轮廓检测
边缘检测 什么是边缘: * 图像中像素值发生剧烈变化的位置(高频信息区域) * 这些区域往往都是图像的边缘 方法:滤波、形态学处理等 边缘的作用 本质上,边缘是不同区域之间的边界。 其中包含了图像的区域信息,形状信息 一方面,可以利用这些信息来作为特征对图像进行理解(甚至…...
二分法模板以及例题 (三)
167. 两数之和 II - 输入有序数组 输入:numbers [2,7,11,15], target 9 输出:[1,2]。 解释:2 与 7 之和等于目标数 9 。因此 index1 1, index2 2 。返回 [1, 2] 解题思路:首先散列表可以直接秒了,双指针也秒了 二分…...
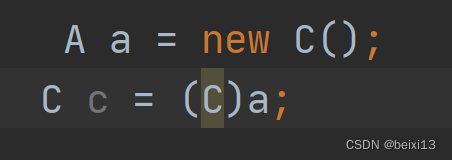
向下转型和向上转型(易理解)
向上转型:父类引用指向子类对象 定义A B C D 四个类,分级继承 对象 a 的编译类型是A,运行类型是B,A是B的父类,父类的引用 a 指向的是B这个子类的对象,因为new的是B这个类,创建的也就是B这个类的…...

华为OD机试用JS实现 -【机智的外卖员】(2023-Q2 押题)
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南华为od机试,独家整理 已参加机试人员的实战技巧本篇题解:机智的外卖员 题目描述: 外…...

同态加密:一个基于多方计算的CKKS方案
这篇文章主要介绍LattiGo团队搞出来的一个多方同态加密的工作。个人觉得比较优雅,而且有库支持,方便把玩,所以记一下。 在攒毕业论文的时候整了这么个看上去很烂,但是(个人觉得)有一点意思的烂活࿰…...
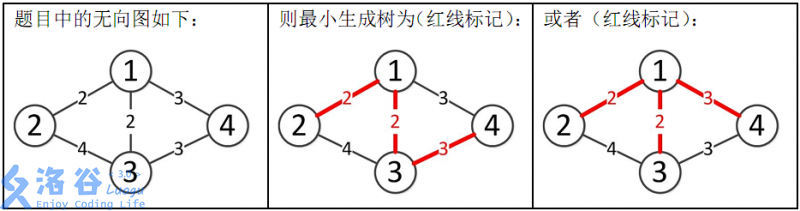
最小生成数
题目描述 如题,给出一个无向图,求出最小生成树,如果该图不连通,则输出 orz。 输入格式 第一行包含两个整数 �,�N,M,表示该图共有 �N 个结点和 �M 条无向边。 接下来 …...
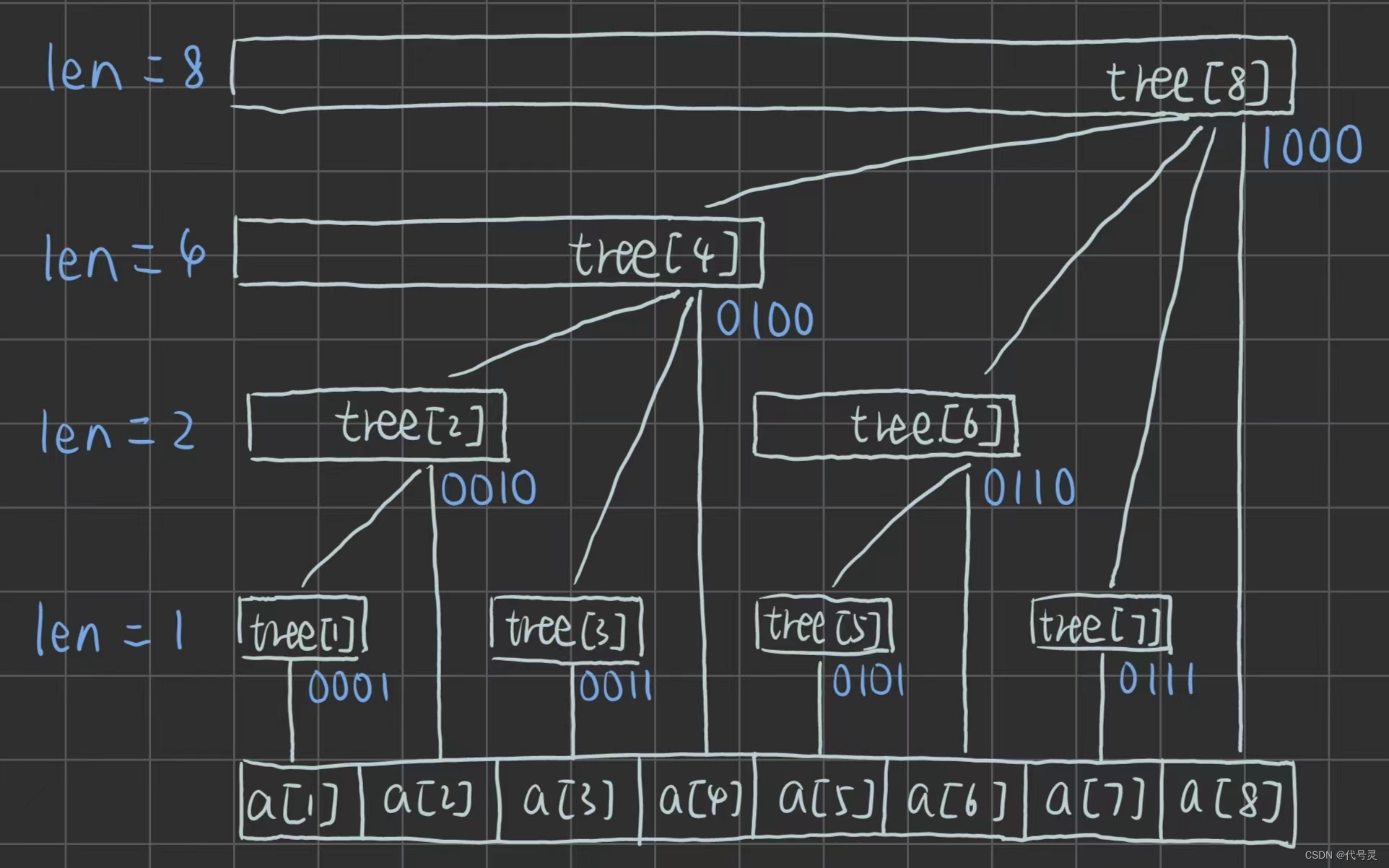
【模板】树状数组
目录: 单点修改,区间查询: 题目描述: lowbit()运算: 插入、修改单点数据: 计算前缀和: 完整代码: 区间修改,单点查询: 计算差分数组: 计算每个点的…...

网站都变成灰色了,怎么实现的?
有些时候我们需要把网站页面变成黑白色或灰色,特别是对于一些需要悼念的日子,以及一些影响力很大的伟人逝世或纪念日的时候,都会让网站的全部网页变成灰色(黑白色),以表示我们对逝者或者英雄的缅怀和悼念。…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

以下是对华为 HarmonyOS NETX 5属性动画(ArkTS)文档的结构化整理,通过层级标题、表格和代码块提升可读性:
一、属性动画概述NETX 作用:实现组件通用属性的渐变过渡效果,提升用户体验。支持属性:width、height、backgroundColor、opacity、scale、rotate、translate等。注意事项: 布局类属性(如宽高)变化时&#…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...

在 Visual Studio Code 中使用驭码 CodeRider 提升开发效率:以冒泡排序为例
目录 前言1 插件安装与配置1.1 安装驭码 CodeRider1.2 初始配置建议 2 示例代码:冒泡排序3 驭码 CodeRider 功能详解3.1 功能概览3.2 代码解释功能3.3 自动注释生成3.4 逻辑修改功能3.5 单元测试自动生成3.6 代码优化建议 4 驭码的实际应用建议5 常见问题与解决建议…...

【免费数据】2005-2019年我国272个地级市的旅游竞争力多指标数据(33个指标)
旅游业是一个城市的重要产业构成。旅游竞争力是一个城市竞争力的重要构成部分。一个城市的旅游竞争力反映了其在旅游市场竞争中的比较优势。 今日我们分享的是2005-2019年我国272个地级市的旅游竞争力多指标数据!该数据集源自2025年4月发表于《地理学报》的论文成果…...
