坐标系变换总结
二维情况下的转换
1 缩放变换
形象理解就是图像在x方向和y方向上放大或者缩小。
代数形式:
{ x ′ = k x x y ′ = k y y \begin{cases} x' = k_x x \\ y' = k_y y \end{cases} {x′=kxxy′=kyy
矩阵形式:
( x ′ y ′ ) = ( k x 0 0 k y ) ( x y ) \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} k_x & 0 \\ 0 & k_y \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} (x′y′)=(kx00ky)(xy)
当 k x = k y k_x = k_y kx=ky 时,是均匀缩放,两个方向同等比例地缩放。
当 k x = − 1 , k y = 1 k_x = -1, k_y = 1 kx=−1,ky=1 ,是镜像变换,类似整个二维平面的图像以y轴为对称轴对称过去一样。
2 切变
平行力作用在物体上的形变
矩阵形式:
( x ′ y ′ ) = ( k x a 0 k y ) ( x y ) = ( k x x + a y k y y ) \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} k_x & a \\ 0 & k_y \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} k_x x + ay \\ k_y y \end{pmatrix} (x′y′)=(kx0aky)(xy)=(kxx+aykyy)
x方向上位置坐标整体向右平移。
3 旋转
旋转是指绕着 原点 逆时针旋转 θ \theta θ 的变换。
旋转矩阵如下:
R = ( c o s θ − s i n θ s i n θ c o s θ ) R = \begin{pmatrix} cos \theta & -sin\theta \\ sin \theta & cos \theta \end{pmatrix} R=(cosθsinθ−sinθcosθ)
( x ′ y ′ ) = ( c o s θ − s i n θ s i n θ c o s θ ) ( x y ) \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} cos \theta & -sin\theta \\ sin \theta & cos \theta \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} (x′y′)=(cosθsinθ−sinθcosθ)(xy)
旋转矩阵是正交阵(转置矩阵等于逆矩阵 R T = R − 1 R^T = R^{-1} RT=R−1)
正交矩阵性质:
- 转置等于逆,绕某个轴旋转 θ \theta θ 的旋转矩阵的逆,就是绕同一轴旋转 − θ -\theta −θ
- 保持向量长度:作用于任何向量时,向量长度不变
- 列向量(行向量)正交且单位化
4 线性变换
线性变换的理解:参考 https://segmentfault.com/a/1190000041138293
线性映射是由向量空间 V → W V\rightarrow W V→W 的映射,而线性变换是线性映射的一个特例,是由线性空间 V V V 到其自身的映射。
通俗理解线性变换就是 坐标轴经过 旋转,伸缩 等操作,原坐标轴上的点一同随着变化,然后这些点会在一个新的位置。
( x ′ y ′ ) = ( a b c d ) ( x y ) = ( a x + b y c y + d y ) \begin{pmatrix} x' \\ y' \end{pmatrix} = \begin{pmatrix} a & b \\ c & d \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} ax + by \\ cy + dy \end{pmatrix} (x′y′)=(acbd)(xy)=(ax+bycy+dy)
其中 ( a , c ) , ( b , d ) (a,c),(b,d) (a,c),(b,d) 是新的坐标系下的基方向上的向量。
线性变换的特点:
- 变换前是直线,变换后依然是直线
- 原点保持固定不动
举个例子:
原坐标轴x轴和y轴,两个基为 i = ( 1 , 0 ) , j = ( 0 , 1 ) i=(1,0), j=(0,1) i=(1,0),j=(0,1) ,这个轴上的某个向量为 A → = ( 3 , 2 ) T = 3 i + 2 j \overrightarrow A = (3,2)^T = 3i+2j A=(3,2)T=3i+2j

现在坐标轴有一个线性变换,新的基为 i ′ = ( 1 , − 2 ) , j ′ = ( 3 , 0 ) i'=(1,-2), j'=(3,0) i′=(1,−2),j′=(3,0) ,此时得到的新的向量,但是它相对于基的关系还是不变的,即 A → ′ = 3 i ′ + 2 j ′ \overrightarrow A' = 3i' + 2j' A′=3i′+2j′
新的 A → ′ \overrightarrow A' A′ 在原坐标系(基)下的坐标可以通过矩阵乘法求得:
A → ′ = ( 1 3 − 2 0 ) ( 3 2 ) \overrightarrow A' = \begin{pmatrix} 1 & 3 \\ -2 & 0 \end{pmatrix} \begin{pmatrix} 3 \\ 2 \end{pmatrix} A′=(1−230)(32)

也就是说这个线性变换矩阵是由新的基向量(说基可能不准确,因为基要求模长为1)组成的列向量。
二维线性变换不涉及到平移变换,即二维下的仿射变换不是线性变换。
5 齐次坐标变换
平移变换无法用单独的矩阵相乘的形式表示,因此引入齐次坐标,增加一维。
二维坐标一般被表示为 ( x , y , w ) (x,y,w) (x,y,w) ,w是一个非零的缩放因子,一般情况下取w=1
平移矩阵:平移(tx, ty)的齐次变换矩阵
T = ( 1 0 t x 0 1 t y 0 0 1 ) ( x ′ y ′ 1 ) = ( 1 0 t x 0 1 t y 0 0 1 ) ( x y 1 ) T = \begin{pmatrix} 1 & 0 & tx \\ 0 & 1 & ty \\ 0 & 0 & 1 \end{pmatrix} \\ \begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} = \begin{pmatrix} 1 & 0 & tx \\ 0 & 1 & ty \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} T= 100010txty1 x′y′1 = 100010txty1 xy1
6 仿射变换
一个向量空间进行一次线性变换并接上一个平移,变换到另一个向量空间。
( x ′ y ′ 1 ) = ( a b t x c d t y 0 0 1 ) ( x y 1 ) \begin{pmatrix} x' \\ y' \\ 1 \end{pmatrix} = \begin{pmatrix} a & b & t_x \\ c & d & t_y \\ 0 & 0 & 1 \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} x′y′1 = ac0bd0txty1 xy1
7 组合变换
可以通过矩阵相乘,将多种变换组合在一起,只需将齐次坐标与最终的变换矩阵相乘即可。注意矩阵是从右向左计算的,矩阵是左乘。
可以将一个变换分解:让矩阵按照某一点进行旋转(先将旋转点平移到原点,然后再平移回去)
三维情况下的转换
1 线性齐次变换
变换矩阵如下:
T = ( x 1 x 2 x 3 0 y 1 y 2 y 3 0 z 1 z 2 z 3 0 0 0 0 1 ) T= \begin{pmatrix} x_{1} & x_2 & x_{3} & 0 \\\ y_{1} & y_2 & y_{3} & 0 \\\ z_{1} & z_2 & z_{3} & 0 \\\ 0 & 0 & 0 & 1 \end{pmatrix} T= x1 y1 z1 0x2y2z20x3y3z300001
( x 1 , y 1 , z 1 ) , ( x 2 , y 2 , z 2 ) , ( x 3 , y 3 , z 3 ) (x_1,y_1,z_1),(x_2,y_2, z_2),(x_3,y_3,z_3) (x1,y1,z1),(x2,y2,z2),(x3,y3,z3) 是新的基向量,即要变换到的坐标系。
将点坐标左乘一个线性变换矩阵,通俗讲就是将原坐标系下的点通过旋转伸长等操作(转到新的坐标系下),求在新坐标系下点的坐标,这个坐标是相对于原坐标系而言的。
同时还可以附加平移操作,新的变换矩阵就是
T = ( x 1 x 2 x 3 t x y 1 y 2 y 3 t y z 1 z 2 z 3 t z 0 0 0 1 ) T= \begin{pmatrix} x_{1} & x_2 & x_{3} & t_x \\\ y_{1} & y_2 & y_{3} & t_y \\\ z_{1} & z_2 & z_{3} & t_z \\\ 0 & 0 & 0 & 1 \end{pmatrix} T= x1 y1 z1 0x2y2z20x3y3z30txtytz1
2 旋转变换

任何一个3D旋转都可以表示成绕x轴,y轴,z轴旋转的组合
R x y z ( α , β , γ ) = R x ( α ) R y ( β ) R z ( γ ) R_{xyz}(\alpha, \beta, \gamma) = R_x(\alpha)R_y(\beta)R_z(\gamma) Rxyz(α,β,γ)=Rx(α)Ry(β)Rz(γ)
α β γ \alpha \beta \gamma αβγ 分别代表物体绕x、y、z旋转的角度,它们也被称为欧拉角
相关文章:

坐标系变换总结
二维情况下的转换 1 缩放变换 形象理解就是图像在x方向和y方向上放大或者缩小。 代数形式: { x ′ k x x y ′ k y y \begin{cases} x k_x x \\ y k_y y \end{cases} {x′kxxy′kyy 矩阵形式: ( x ′ y ′ ) ( k x 0 0 k y ) ( x y ) \be…...

数据在内存中的存储【上】
一.整型在内存中的存储 在讲解操作符的时候,我们就讲过了下面的内容: 整数的2进制表示方法有三种,即 原码、反码和补码 有符号的整数,三种表示方法均有符号位和数值位两部分,符号位都是用0表示"正"ÿ…...

Prometheus之Pushgateway使用
Pushgateway属于整个架构图的这一部分 The Pushgateway is an intermediary service which allows you to push metrics from jobs which cannot be scraped. The Prometheus Pushgateway exists to allow ephemeral and batch jobs to expose their metrics to Prometheus. S…...

Rust Web开发常用库
本集合中所有库都是在开源项目中广泛使用且在2024年积极维护的库,排名靠前的库是当前使用比较广泛的,不全面但够用 Rust异步运行时 tokio:异步运行时 async_std:与标准库兼容性较强的运行时 monoio:字节开源 smol…...

ios内购支付-支付宝APP支付提现
文章目录 前言一、IOS内购支付(ios订单生成自己写逻辑即可)1.支付回调票据校验controller1.支付回调票据校验server 二、安卓APP支付宝支付1.生成订单返回支付宝字符串(用于app拉起支付宝,这里用的是证书模式)2.生成订…...

新课发布|鸿蒙HarmonyOS Next商城APP应用开发实战
2024年年初,鸿蒙HarmonyOS Next星河版强势发布,随着鸿蒙系统的普及和应用场景的拓展,市场需求将持续增加。鸿蒙系统已经应用于华为的智能手机、平板电脑、智能家居等多个领域,并有望在未来拓展到智能汽车、物联网等更多领域。这为…...

基于Java,SpringBoot,Vue智慧校园健康驿站体检论坛请假管理系统
摘要 互联网发展至今,无论是其理论还是技术都已经成熟,而且它广泛参与在社会中的方方面面。它让信息都可以通过网络传播,搭配信息管理工具可以很好地为人们提供服务。针对信息管理混乱,出错率高,信息安全性差…...
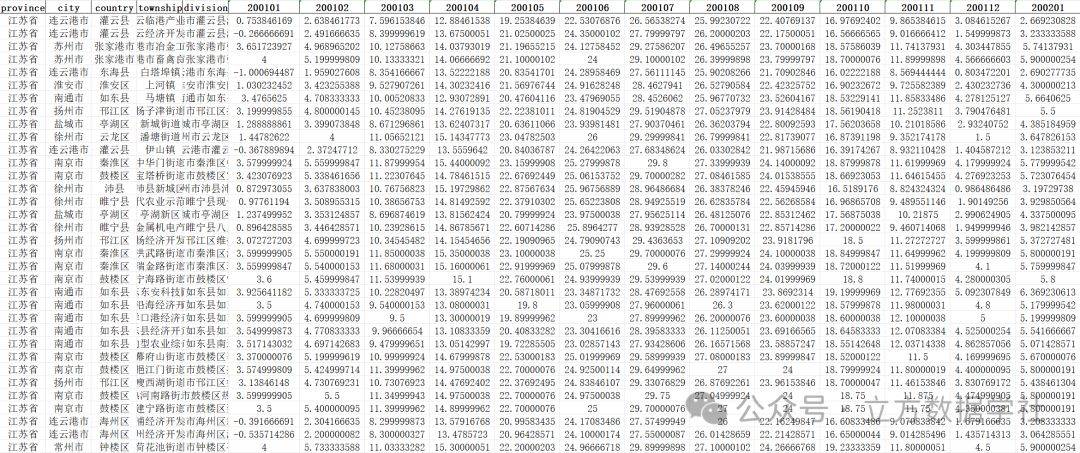
【数据分享】2001-2023年我国省市县镇四级的逐月平均气温数据(免费获取/Shp/Excel格式)
之前我们分享过1901-2023年1km分辨率逐月平均气温栅格数据,该数据来源于国家青藏高原科学数据中心。为方便大家使用,我们还基于上述平均气温栅格数据将数据处理为Shp和Excel格式的省市县三级逐月平均气温数据(可查看之前的文章获悉详情&#…...

c#代码介绍23种设计模式_16迭代器模式
目录 1、迭代器模式的介绍 2、迭代器模式的定义 3、迭代器模式的结构 4、代器模式角色组成 5、迭代器实现 6、迭代器模式的适用场景 7、迭代器模式的优缺点 8、.NET中迭代器模式的应用 9、实现思路 1、迭代器模式的介绍 迭代器是针对集合对象而生的,对于集合对象而言…...

408算法题leetcode--第23天
236. 二叉树的最近公共祖先 236. 二叉树的最近公共祖先\思路:递归,如注释时间和空间:O(n) /*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode(int x) …...
帝国CMS系统开启https后,无法登陆后台的原因和解决方法
今天本地配置好了帝国CMS7.5,传去服务器后,使用http访问一切正常。但是当开启了https(SSL)后,后台竟然无法登陆进去了。 输入账号密码后,点击登陆,跳转到/e/admin/ecmsadmin.php就变成页面一片…...

根据视频id查询播放量
声明:文章仅用于学习交流,如有侵权请联系删除 如何根据视频ID查询视频的播放数量 在数字化时代,视频内容的消费已成为人们日常生活的重要组成部分。无论是社交媒体平台上的短视频,还是视频分享网站上的长视频,了解视频的播放数量…...

初始爬虫11
1.斗鱼selenium爬取 # -*- coding: utf-8 -*- from selenium import webdriver from selenium.webdriver.common.by import By import timeclass Douyu(object):def __init__(self):self.url https://www.douyu.com/directory/allself.driver webdriver.Chrome()self.driver…...

SSY20241002提高组T4题解__纯数论
题面 题目描述 有一天 p e o p 1 e peop1e peop1e 学长梦到了一个丑陋的式子: ∑ i 1 n ( ∑ m 1 R F m ) ! i ! ∑ l 0 i ∑ j 0 ∑ t 1 R F t { K i − l } l ! { i ∑ w 1 R F w − j } j ! \sum_{i1}^n (\sum_{m1}^R F_m)!\times i!\times \sum_{l…...

Python:lambda 函数详解 以及使用
一、lambda 语法 lambda 函数的语法只包含一个语句,表现形式如下: lambda [arg1 [,arg2,.....argn]]:expression 其中,lambda 是 Python 预留的关键字,[arg…] 和 expression 由用户自定义。 具体如下: [arg…] 是参数列表&#…...

【C++】空指针和野指针
文章目录 1.空指针2.野指针总结 1.空指针 概念:指针变量指向内存中编号为0的空间。 用途:初始化指针变量。 注意:空指针指向的内存是不可以访问的。 示例: int main(){//指针变量p指向内存地址编号为0的空间int *PNULL&#…...

大模型提示词
纯输入版提示工程词 输出一个九九乘法口诀表 当然可以!以下是九九乘法口诀表: 1 x 1 1 1 x 2 2 2 x 2 4 1 x 3 3 2 x 3 6 3 x 3 9 1 x 4 4 2 x 4 8 3 x 4 12 4 x 4 16 1 x 5 5 2 x 5 10 3 x 5 15 4 x 5 20 5 …...

在线css像素px到Em的转换器
具体请前往:在线Px转Em工具--将绝对像素(px)长度单位转换为相对长度em...

回溯算法解决排列组合及子集问题
216. 组合总和 III39. 组合总和40. 组合总和 II46. 全排列47. 全排列 II77. 组合 78. 子集 90. 子集 II 以上是力扣设计相关问题的题目。排列组合还是子集问题无非就是从序列 nums 中以给定规则取若干元素,主要有以下几类: 元素无重不可复选࿰…...

Unity中Mesh多种网格绘制模式使用方法参考
Unity中MeshFilter中的Mesh默认情况下使用MeshTopology.Trigangles类型绘制网格,就是通常的绘制三角形网格,实际上Mesh有五种绘制模式,对应MeshTopology的枚举,分别是 Triangles网格由三角形构成。Quads网格由四边形构成。Lines网…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

深度学习之模型压缩三驾马车:模型剪枝、模型量化、知识蒸馏
一、引言 在深度学习中,我们训练出的神经网络往往非常庞大(比如像 ResNet、YOLOv8、Vision Transformer),虽然精度很高,但“太重”了,运行起来很慢,占用内存大,不适合部署到手机、摄…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...
