SSY20241002提高组T4题解__纯数论
题面
题目描述
有一天 p e o p 1 e peop1e peop1e 学长梦到了一个丑陋的式子:
∑ i = 1 n ( ∑ m = 1 R F m ) ! × i ! × ∑ l = 0 i ∑ j = 0 ∑ t = 1 R F t { K i − l } l ! { i ∑ w = 1 R F w − j } j ! = \sum_{i=1}^n (\sum_{m=1}^R F_m)!\times i!\times \sum_{l=0}^i \sum_{j=0}^{\sum_{t=1}^R F_t}\frac{{K}\brace{i-l}}{l!}\frac{{i}\brace{\sum_{w=1}^R F_w-j}}{j!}= i=1∑n(m=1∑RFm)!×i!×l=0∑ij=0∑∑t=1RFtl!{i−lK}j!{∑w=1RFw−ji}=
其中 F i F_i Fi 表示斐波那契数列的第 i i i项, F 0 = 0 , F 1 = 1 , F 2 = 1 F_0 = 0, F_1 = 1, F_2 = 1 F0=0,F1=1,F2=1,
{ n m } {n}\brace{m} {mn}表示第二类斯特林数, 其值为将 n n n 个不同元素放入 m m m 个集合的方案数。
他想了很久都没有想出来, 于是拿来请教你。如果你做出来了, 他会请你吃饭。
答案对 1 0 9 + 7 10^9 + 7 109+7 取模。
输入输出格式
输入
一行三个正整数 n , R , K n, R, K n,R,K
输出
一个正整数, 表示答案。
输出输出扬样例
输入1
4 5 2
3 5 2
输出1
347916
输入2
94082 698 850
输出2
93954859
数据范围
对于10% 的数据, n , R , K ≤ 5 n, R, K ≤ 5 n,R,K≤5
对于30% 的数据, n , R ≤ 1 0 5 , K ≤ 200 n, R ≤ 10^5, K ≤ 200 n,R≤105,K≤200
对于另10% 的数据, n ≤ 1 0 18 , K ≤ 200 , R ≤ 1 0 5 n ≤ 10^{18}, K ≤ 200, R ≤ 10^5 n≤1018,K≤200,R≤105
对于另10% 的数据, n ≤ 1 0 18 , K ≤ 200 , R ≤ 1 0 18 n ≤ 10^{18}, K ≤ 200, R ≤ 10^{18} n≤1018,K≤200,R≤1018
对于另10% 的数据, n ≤ 1 0 18 , K ≤ 200 , R = 1 n ≤ 10^{18}, K ≤ 200, R = 1 n≤1018,K≤200,R=1
对于70% 的数据, n ≤ 1 0 18 , K ≤ 2000 , R ≤ 1 0 18 n ≤ 10^{18}, K ≤ 2000, R ≤ 10^{18} n≤1018,K≤2000,R≤1018
对于100% 的数据, n ≤ 1 0 18 , K ≤ 200000 , R ≤ 1 0 18 n ≤ 10^{18}, K ≤ 200000, R ≤ 10^{18} n≤1018,K≤200000,R≤1018
题解
解析
前置知识
-
∑ i = 1 n F i = F n + 2 − 1 \sum_{i=1}^nF_i=F_{n+2}-1 i=1∑nFi=Fn+2−1证明:数学归纳法
当 n = 1 n=1 n=1 时显然成立
假设 n = m n=m n=m 时此式子成立
∑ i = 1 m + 1 F i = ∑ i = 1 m F i + F m + 1 = F m + 2 + F m + 1 − 1 = F m + 3 − 1 \begin{aligned} &\sum_{i=1}^{m+1}F_i \\ =&\sum_{i=1}^mF_i+F_{m+1} \\ =&F_{m+2}+F_{m+1}-1 \\ =&F_{m+3}-1 \end{aligned} ===i=1∑m+1Fii=1∑mFi+Fm+1Fm+2+Fm+1−1Fm+3−1 -
m n = ∑ i = 1 m C m i × { n i } × i m^n=\sum_{i=1}^mC_m^{\;i}\times{{n}\brace{i}}\times i\! mn=i=1∑mCmi×{in}×i
根据小球与盒子相关例题可以轻松理解 -
拉格朗日插值
不会只会30分
现在开始正式推导~~(请耐心观看)~~
令 L = ∑ m = 1 R F m L=\sum^R_{m=1}F_m L=∑m=1RFm ,原式变为
∑ i = 1 n L ! × i ! × ∑ l = 0 i ∑ j = 0 L ( { K i − l } l ! × { i L − j } j ! ) = ∑ i = 1 n L ! × i ! × ( ∑ l = 0 i { K i − l } l ! ) × ( ∑ j = 0 L { i L − j } j ! ) = ∑ i = 1 n ( ∑ l = 0 i { K i − l } l ! × i ! ) × ( ∑ j = 0 L { i L − j } j ! × L ! ) = ∑ i = 1 n ( ∑ l = 0 i i ! l ! × { K i − l } ) × ( ∑ j = 0 L L ! j ! × { i L − j } ) \begin{aligned} &\sum_{i=1}^n L!\times i!\times \sum_{l=0}^i \sum_{j=0}^L\bigg(\frac{{K}\brace{i-l}}{l!}\times \frac{{i}\brace{L-j}}{j!}\bigg) \\ =&\sum_{i=1}^n L!\times i!\times\bigg(\sum_{l=0}^i\frac{{K}\brace{i-l}}{l!}\bigg)\times\bigg(\sum_{j=0}^L\frac{{i}\brace{L-j}}{j!}\bigg) \\ =&\sum_{i=1}^n\bigg(\sum_{l=0}^i\frac{{K}\brace{i-l}}{l!}\times i!\bigg)\times\bigg(\sum_{j=0}^L\frac{{i}\brace{L-j}}{j!}\times L!\bigg) \\ =&\sum_{i=1}^n\bigg(\sum_{l=0}^i\frac{i!}{l!}\times {{K}\brace{i-l}}\bigg) \times\bigg(\sum_{j=0}^L\frac{L!}{j!}\times {{i}\brace{L-j}}\bigg) \end{aligned} ===i=1∑nL!×i!×l=0∑ij=0∑L(l!{i−lK}×j!{L−ji})i=1∑nL!×i!×(l=0∑il!{i−lK})×(j=0∑Lj!{L−ji})i=1∑n(l=0∑il!{i−lK}×i!)×(j=0∑Lj!{L−ji}×L!)i=1∑n(l=0∑il!i!×{i−lK})×(j=0∑Lj!L!×{L−ji})我们假设 l , j l,j l,j 是倒着枚举的, 推为:
(也可以认为在枚举 l l l 的时候也会枚举到 i − l i-l i−l 的所有之)
= ∑ i = 1 n ( ∑ l = 0 i i ! ( i − l ) ! × { K l } ) × ( ∑ j = 0 L L ! ( L − j ) ! × { i j } ) = ∑ i = 1 n ( ∑ l = 0 i i ! ( i − l ) ! × l ! × { K l } × l ! ) × ( ∑ j = 0 L L ! ( L − j ) ! × j ! × { i j } × j ! ) = ∑ i = 1 n ( ∑ l = 0 i C i l × { K l } × l ! ) × ( ∑ j = 0 L C L j × { i j } × j ! ) = ∑ i = 1 n i k L i \begin{aligned} =&\sum_{i=1}^n\bigg(\sum_{l=0}^i\frac{i!}{(i-l)!}\times {{K}\brace{l}}\bigg) \times\bigg(\sum_{j=0}^L\frac{L!}{(L-j)!}\times {{i}\brace{j}}\bigg) \\ =&\sum_{i=1}^n\bigg(\sum_{l=0}^i\frac{i!}{(i-l)!\times l!}\times {{K}\brace{l}}\times l!\bigg) \times\bigg(\sum_{j=0}^L\frac{L!}{(L-j)!\times j!}\times {{i}\brace{j}}\times j!\bigg) \\ =&\sum_{i=1}^n\bigg(\sum_{l=0}^iC^l_i\times {{K}\brace{l}}\times l!\bigg) \times\bigg(\sum_{j=0}^LC^j_L\times {{i}\brace{j}}\times j!\bigg) \\ =&\sum_{i=1}^ni^kL^i \end{aligned} ====i=1∑n(l=0∑i(i−l)!i!×{lK})×(j=0∑L(L−j)!L!×{ji})i=1∑n(l=0∑i(i−l)!×l!i!×{lK}×l!)×(j=0∑L(L−j)!×j!L!×{ji}×j!)i=1∑n(l=0∑iCil×{lK}×l!)×(j=0∑LCLj×{ji}×j!)i=1∑nikLi
恭喜你 到这里你…
只能拿到30分
接下来是拉格朗日插值
明天补
相关文章:

SSY20241002提高组T4题解__纯数论
题面 题目描述 有一天 p e o p 1 e peop1e peop1e 学长梦到了一个丑陋的式子: ∑ i 1 n ( ∑ m 1 R F m ) ! i ! ∑ l 0 i ∑ j 0 ∑ t 1 R F t { K i − l } l ! { i ∑ w 1 R F w − j } j ! \sum_{i1}^n (\sum_{m1}^R F_m)!\times i!\times \sum_{l…...

Python:lambda 函数详解 以及使用
一、lambda 语法 lambda 函数的语法只包含一个语句,表现形式如下: lambda [arg1 [,arg2,.....argn]]:expression 其中,lambda 是 Python 预留的关键字,[arg…] 和 expression 由用户自定义。 具体如下: [arg…] 是参数列表&#…...

【C++】空指针和野指针
文章目录 1.空指针2.野指针总结 1.空指针 概念:指针变量指向内存中编号为0的空间。 用途:初始化指针变量。 注意:空指针指向的内存是不可以访问的。 示例: int main(){//指针变量p指向内存地址编号为0的空间int *PNULL&#…...

大模型提示词
纯输入版提示工程词 输出一个九九乘法口诀表 当然可以!以下是九九乘法口诀表: 1 x 1 1 1 x 2 2 2 x 2 4 1 x 3 3 2 x 3 6 3 x 3 9 1 x 4 4 2 x 4 8 3 x 4 12 4 x 4 16 1 x 5 5 2 x 5 10 3 x 5 15 4 x 5 20 5 …...

在线css像素px到Em的转换器
具体请前往:在线Px转Em工具--将绝对像素(px)长度单位转换为相对长度em...

回溯算法解决排列组合及子集问题
216. 组合总和 III39. 组合总和40. 组合总和 II46. 全排列47. 全排列 II77. 组合 78. 子集 90. 子集 II 以上是力扣设计相关问题的题目。排列组合还是子集问题无非就是从序列 nums 中以给定规则取若干元素,主要有以下几类: 元素无重不可复选࿰…...

Unity中Mesh多种网格绘制模式使用方法参考
Unity中MeshFilter中的Mesh默认情况下使用MeshTopology.Trigangles类型绘制网格,就是通常的绘制三角形网格,实际上Mesh有五种绘制模式,对应MeshTopology的枚举,分别是 Triangles网格由三角形构成。Quads网格由四边形构成。Lines网…...

【Spring Security】基于SpringBoot3.3.4版本②如何配置免鉴权Path
基于Spring Boot 3.3.4,详细说明Spring Security 6.3.3的使用 摘要本地开发环境说明SecurityFilterChain介绍application.ymlWen3SecurityProperties.java修改DemoWen3Security修改SecurityFilterChainIgnoredPathController.javaIgnoredPathController2.java启动工程测试测试…...
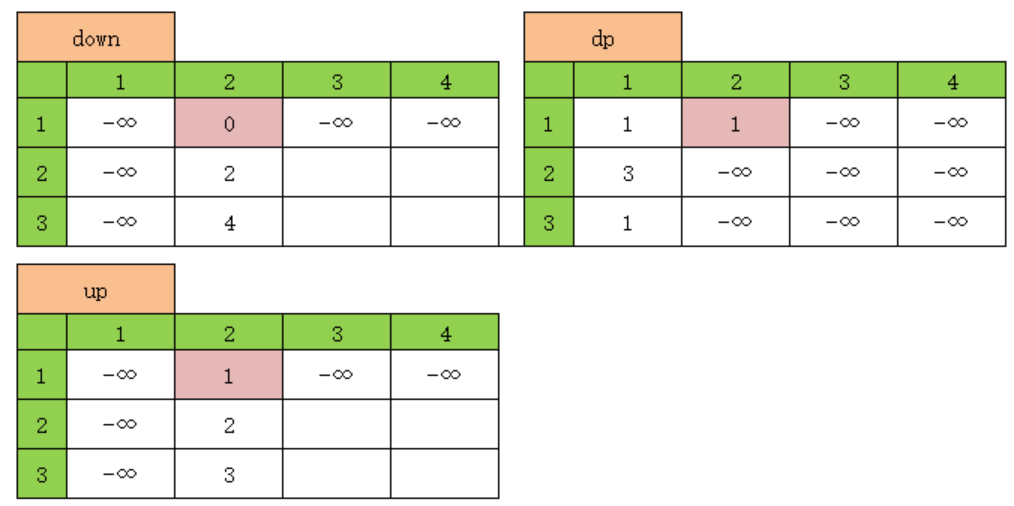
信息学奥赛复赛复习11-CSP-J2020-04方格取数-动态规划、斐波那契数列、最优子结构、重叠子问题、无后效性
PDF文档回复:20241004 1 P7074 [CSP-J2020] 方格取数 [题目描述] 设有 nm 的方格图,每个方格中都有一个整数。现有一只小熊,想从图的左上角走到右下角,每一步只能向上、向下或向右走一格,并且不能重复经过已经走过的方格&#x…...
)
Hive数仓操作(十二)
一、Hive 中的行列转换 1. 行转列: collect_list() collect_list() 函数用于将一个列中的数据收集成一个数组。 示例数据文件 假设有一个名为 orders.txt 的文件,内容如下: 1,101 1,101 1,103 2,104 2,105导入数据到 Hive 表 首先&…...

计算机毕业设计 基于SpringBoot和Vue的课程教学平台的设计与实现 Java实战项目 附源码+文档+视频讲解
博主介绍:✌从事软件开发10年之余,专注于Java技术领域、Python人工智能及数据挖掘、小程序项目开发和Android项目开发等。CSDN、掘金、华为云、InfoQ、阿里云等平台优质作者✌ 🍅文末获取源码联系🍅 👇🏻 精…...

有状态(Session) VS 无状态(Token)
目录 概念 JWT Token在项目中使用 概念 有状态和无状态服务是两种不同的服务架构,两者的不同之处在于对于服务状态的处理。 1、有状态服务 是指程序在执行过程中生成的中间数据,服务器端一般都要保存请求的相关信息,每个请求可以默认地使…...

天坑!Spark+Hive+Paimon+Dolphinscheduler
背景: 数据中台项目使用Spark+Hive+Paimon做湖仓底层,调度任务使用的是基于Dolphinscheduler进行二开。在做离线脚本任务开发时,在Paimon库下执行非查询类SQL报错。 INSERT报错 DELETE报错 现状: 原始逻辑为数据中台中选择的Paimon数据源,实际上在Dolphinscheduler中是…...

JAVA——IO框架
目录 一、框架 二、导入框架步骤 三、测试 一、框架 框架就是为了解决某类问题,编写的一套类、接口等。大多数框架都是第三方研发的 好处: 在框架的基础上开发,提高开发效率 框架的形式:一般是把类、接口编译成class形式,再…...

项目管理系统如何实现项目申报流程自动化?
传统的项目申报流程往往繁琐复杂,涉及众多环节和部门间的协作,不仅耗时费力,还容易因人为疏忽而导致错误或延误。随着信息技术的飞速发展,项目管理系统的出现为项目申报流程的自动化提供了可能,极大地提升了申报效率和…...

ndb9300public-ndb2excel简介
1 引言 ndb9300是一个自己定义的机载导航数据库劳作(不敢称为项目)代号,其中3表示是第3种数据库。 多年前,对在役民航客机中的某型机载导航数据库的二进制文件进行分析,弄明白它的数据结构后做了几个工具,…...

C++:const成员
const修饰成员变量,要在初始化列表中进行初始化。 const修饰成员函数,要放在函数后,称为常函数。常函数不能修改普通成员变量。 const修饰的对象,称为常对象。常对象不能修改普通成员变量,只能读取。 常对象只能使用…...

基于ROS的激光雷达点云物体检测
环境 RTX 2060(后面关于算力) ubuntu 18.04 ROS melodic (ubuntu 18.04安装ROS melodic可以参看我这篇文章ubuntu 18.04安装ROS系统) CUDA 10.0 cudnn 7.6.5 caffe cmake 3.18.0(不能低于3.12.2) opencv 3…...

大模型训练环境搭建
硬件资源说明 本教程基于GPU 3090的服务器 资源类型 型号 核心指标 CPU Intel(R) Xeon(R) Bronze 3204 CPU 1.90GHz 12核 内存 / 125Gi GPU NVIDIA GeForce RTX 3090 24G显存 注意:接下来的部分命令需要使用科学上网,需要事先配置好。 安…...

使用Java调用GeoTools实现全球国家矢量数据入库实战
目录 前言 一、相关数据介绍 1、无空间参考的数据 2、有空间参考的数据 3、空间信息表物理模型 二、全球国家空间数据入库 1、后台实体类图 2、后台实体对象关键代码 三、时空数据入库实践 1、读取无空间参考数据 2、入库成果及注意事项 四、总结 前言 在当今世界&…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

TSN交换机正在重构工业网络,PROFINET和EtherCAT会被取代吗?
在工业自动化持续演进的今天,通信网络的角色正变得愈发关键。 2025年6月6日,为期三天的华南国际工业博览会在深圳国际会展中心(宝安)圆满落幕。作为国内工业通信领域的技术型企业,光路科技(Fiberroad&…...
