LeetCode从入门到超凡(五)深入浅出---位运算

引言

大家好，我是GISer Liu😁，一名热爱AI技术的GIS开发者。本系列文章是我跟随DataWhale 2024年9月学习赛的LeetCode学习总结文档；本文主要讲解 位运算算法。💕💕😊

---

一、 位运算简介

1.什么是位运算？

① 位运算的定义

位运算（Bit Operation）是指直接对整数的二进制位进行操作的运算。在计算机内部，所有的数据都是以二进制形式存储的，因此位运算可以直接操作这些二进制位，从而实现一些高效的计算。

② 优势：提高程序性能

位运算的优势在于其高效性。由于位运算是直接对二进制位进行操作，不需要进行复杂的数值转换，因此在某些情况下，使用位运算可以显著提高程序的性能。例如，在处理大量数据或需要频繁进行位操作的场景中，位运算可以大大减少计算时间。

2.二进制数的基本概念

① 二进制数的表示方法

二进制数（Binary）是由 0 和 1 两个数码组成的数。在计算机中，所有的数据最终都会被转换为二进制形式进行存储和处理。

② 二进制数的位（Bit）

在二进制数中，每一个 0 或 1 被称为一个位（Bit）。位是二进制数的最小单位，多个位组合在一起可以表示更大的数值。

① 二进制与十进制的区别

• 十进制：由 0 到 9 共 10 个数码组成，进位规则是“满十进一”。例如，7 + 2 = 9，9 + 2 = 11。
• 二进制：由 0 和 1 两个数码组成，进位规则是“逢二进一”。例如，1 + 0 = 1，1 + 1 = 10。

② 二进制的进位规则：逢二进一

在二进制中，当某一位的数值达到 2 时，就会向高位进一。例如：

• 1 + 0 = 1
• 1 + 1 = 10（相当于十进制的 2）
• 10 + 1 = 11（相当于十进制的 3）

③ 示例：二进制数的加法

让我们通过一个简单的例子来理解二进制数的加法：

  101 (二进制)
+ 011 (二进制)
------1000 (二进制)

在这个例子中：

• 最低位 1 + 1 = 10，结果是 0，进位 1。
• 第二位 0 + 1 + 进位 1 = 10，结果是 0，进位 1。
• 第三位 1 + 0 + 进位 1 = 10，结果是 0，进位 1。
• 最高位只有进位 1，结果是 1。

最终结果是 1000，即十进制的 8。

---

3. 二进制数的转换

① 二进制转十进制

转换方法：按权展开

将二进制数转换为十进制数的方法是按权展开。每一位的权值是 2 的幂次方，从右到左依次为 2^0, 2^1, 2^2, …。

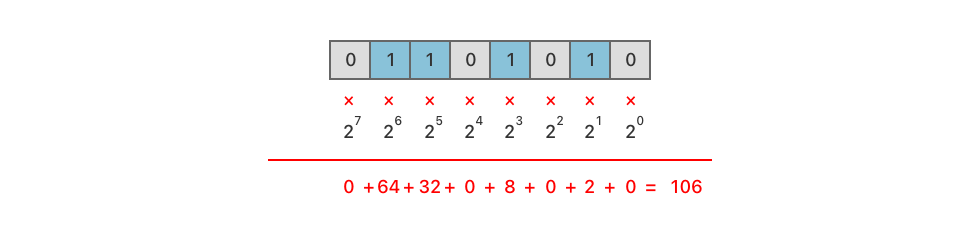
示例：二进制数 01101010 转换为十进制

二进制数：01101010
按权展开：
0 * 2^7 + 1 * 2^6 + 1 * 2^5 + 0 * 2^4 + 1 * 2^3 + 0 * 2^2 + 1 * 2^1 + 0 * 2^0
= 0 + 64 + 32 + 0 + 8 + 0 + 2 + 0
= 106

所以，二进制数 01101010 转换为十进制数是 106。

② 十进制转二进制

转换方法：除二取余，逆序排列

将十进制数转换为二进制数的方法是“除二取余，逆序排列”。具体步骤如下：

1. 将十进制数不断除以 2，记录每次的余数。
2. 将所有余数逆序排列，得到二进制数。

示例：十进制数 106 转换为二进制

106 ÷ 2 = 53 余 053 ÷ 2 = 26 余 126 ÷ 2 = 13 余 013 ÷ 2 = 6  余 16 ÷ 2 = 3  余 03 ÷ 2 = 1  余 11 ÷ 2 = 0  余 1

将余数逆序排列，得到 1101010。由于二进制数通常从高位开始，所以最终结果是 01101010。

所以，十进制数 106 转换为二进制数是 01101010。

通过这些步骤，我们可以理解位运算的基本概念和二进制数的转换方法。接下来，我们将深入探讨位运算的具体操作。

二、位运算基础操作

1.按位与运算（AND）

① 运算符：&

按位与运算使用符号 & 表示。它是一种双目运算符，即需要两个操作数。

② 运算规则

按位与运算的规则是：只有当两个二进位都为 1 时，结果位才为 1。否则，结果位为 0。

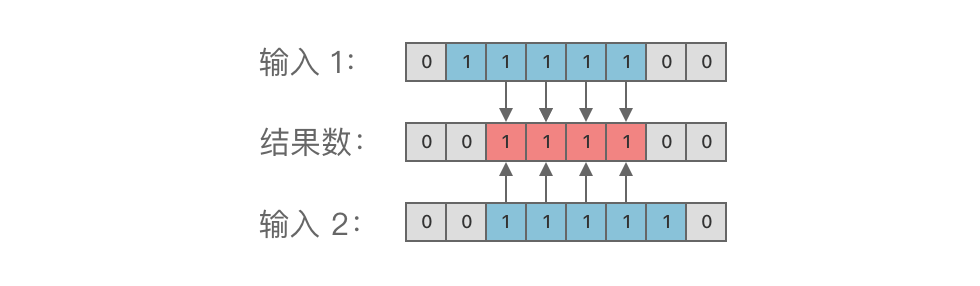
具体规则如下：

• 1 & 1 = 1
• 1 & 0 = 0
• 0 & 1 = 0
• 0 & 0 = 0

③ 示例

让我们通过一个具体的例子来理解按位与运算：

  01111100
& 00111110
----------00111100

逐位进行与运算：

• 第 1 位：0 & 0 = 0
• 第 2 位：0 & 1 = 0
• 第 3 位：1 & 1 = 1
• 第 4 位：1 & 1 = 1
• 第 5 位：1 & 1 = 1
• 第 6 位：1 & 1 = 1
• 第 7 位：1 & 1 = 1
• 第 8 位：0 & 0 = 0

最终结果是 00111100。

2. 按位或运算（OR）

① 运算符：|

按位或运算使用符号 | 表示。它也是一种双目运算符，需要两个操作数。

② 运算规则

按位或运算的规则是：只要有一个二进位为 1，结果位就为 1。否则，结果位为 0。

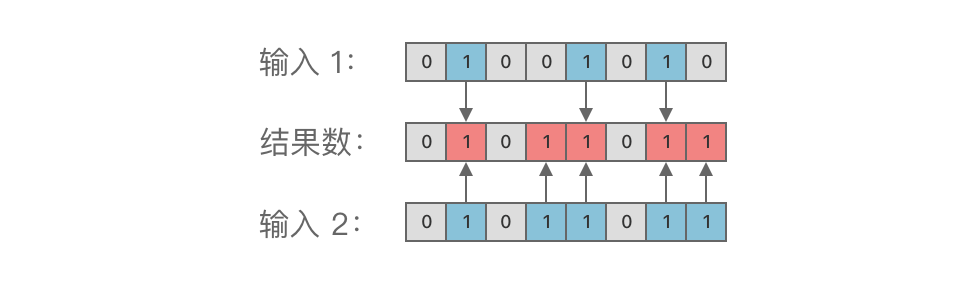
具体规则如下：

• 1 | 1 = 1
• 1 | 0 = 1
• 0 | 1 = 1
• 0 | 0 = 0

③ 示例：

下面通过一个具体的例子来理解按位或运算：

  01001010
| 01011011
----------01011011

逐位进行或运算：

• 第 1 位：0 | 1 = 1
• 第 2 位：1 | 1 = 1
• 第 3 位：0 | 0 = 0
• 第 4 位：0 | 1 = 1
• 第 5 位：1 | 1 = 1
• 第 6 位：0 | 0 = 0
• 第 7 位：1 | 1 = 1
• 第 8 位：0 | 1 = 1

最终结果是 01011011。

3. 按位异或运算（XOR）

① 运算符：^

按位异或运算使用符号 ^ 表示。它也是一种双目运算符，需要两个操作数。

② 运算规则

按位异或运算的规则是：对应的两个二进位相异时，结果位为 1，相同时为 0。

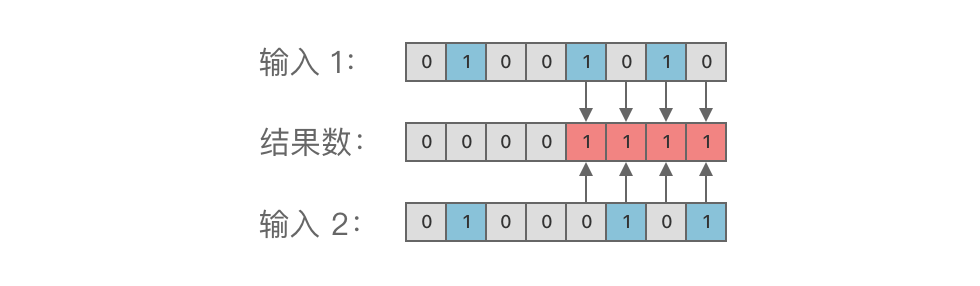
具体规则如下：

• 1 ^ 1 = 0
• 1 ^ 0 = 1
• 0 ^ 1 = 1
• 0 ^ 0 = 0

③ 示例

下例中我们理解按位异或运算：

  01001010
^ 01000101
----------00001111

逐位进行异或运算：

• 第 1 位：0 ^ 1 = 1
• 第 2 位：1 ^ 0 = 1
• 第 3 位：0 ^ 0 = 0
• 第 4 位：0 ^ 0 = 0
• 第 5 位：1 ^ 0 = 1
• 第 6 位：0 ^ 1 = 1
• 第 7 位：1 ^ 0 = 1
• 第 8 位：0 ^ 1 = 1

最终结果是 00001111。

4. 取反运算（NOT）

① 运算符：~

取反运算使用符号 ~ 表示。它是一种单目运算符，只需要一个操作数。

② 运算规则

取反运算的规则是：将 1 变为 0，0 变为 1。

具体规则如下：

• ~0 = 1
• ~1 = 0

③ 示例

让我们通过一个具体的例子来理解取反运算：

~01101010
----------
10010101

逐位进行取反运算：

• 第 1 位：~0 = 1
• 第 2 位：~1 = 0
• 第 3 位：~1 = 0
• 第 4 位：~0 = 1
• 第 5 位：~1 = 0
• 第 6 位：~0 = 1
• 第 7 位：~1 = 0
• 第 8 位：~0 = 1

最终结果是 10010101。

5. 左移运算（SHL）

① 运算符：<<

左移运算使用符号 << 表示。它是一种双目运算符，需要一个操作数和一个移位次数。

② 运算规则

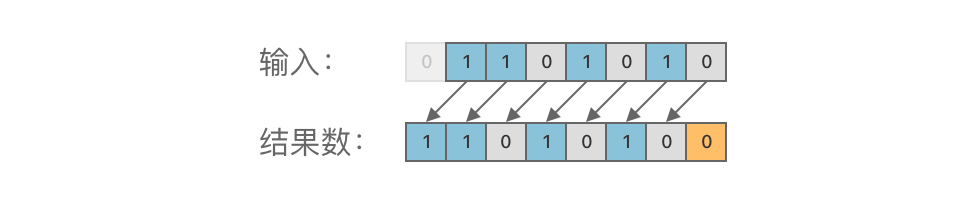
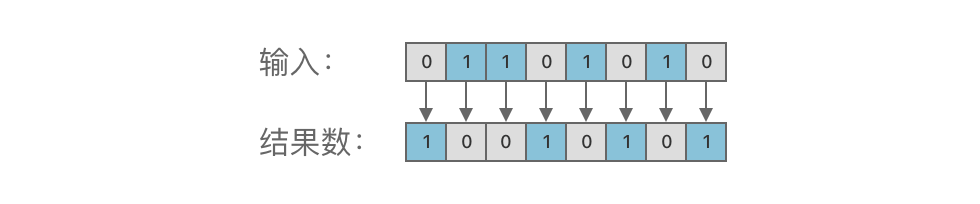
左移运算的规则是：将二进制数的各个二进位全部左移若干位，高位丢弃，低位补 0。

③ 示例：01101010 左移 1 位

让我们通过一个具体的例子来理解左移运算：

01101010 << 1
----------
11010100

逐位进行左移运算：

• 第 1 位：0 移出，高位丢弃
• 第 2 位：1 移到第 1 位
• 第 3 位：1 移到第 2 位
• 第 4 位：0 移到第 3 位
• 第 5 位：1 移到第 4 位
• 第 6 位：0 移到第 5 位
• 第 7 位：1 移到第 6 位
• 第 8 位：0 移到第 7 位
• 低位补 0

最终结果是 11010100。

6. 右移运算（SHR）

① 运算符：>>

右移运算使用符号 >> 表示。它也是一种双目运算符，需要一个操作数和一个移位次数。

② 运算规则

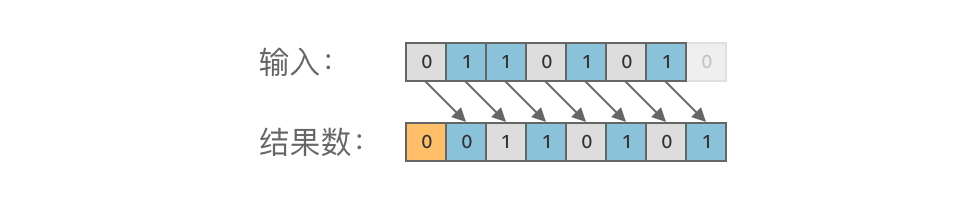
右移运算的规则是：将二进制数的各个二进位全部右移若干位，低位丢弃，高位补 0。

③ 示例：01101010 右移 1 位

让我们通过一个具体的例子来理解右移运算：

01101010 >> 1
----------
00110101

逐位进行右移运算：

• 第 8 位：0 移出，低位丢弃
• 第 7 位：1 移到第 8 位
• 第 6 位：0 移到第 7 位
• 第 5 位：1 移到第 6 位
• 第 4 位：0 移到第 5 位
• 第 3 位：1 移到第 4 位
• 第 2 位：1 移到第 3 位
• 第 1 位：0 移到第 2 位
• 高位补 0

最终结果是 00110101。

---

三、 位运算的应用

1. 位运算的常用操作

① 判断整数奇偶

原理：通过与 1 进行按位与运算

判断一个整数是奇数还是偶数，可以通过与 1 进行按位与运算。如果结果为 0，则该数为偶数；如果结果为 1，则该数为奇数。

示例：判断 x 是奇数还是偶数

def is_even(x):return (x & 1) == 0def is_odd(x):return (x & 1) == 1# 示例
x = 10
print(f"{x} 是偶数吗？", is_even(x))  # 输出：True
print(f"{x} 是奇数吗？", is_odd(x))   # 输出：False

思维流程

② 二进制数选取指定位

原理：使用按位与运算

要选取二进制数中的某几位，可以使用按位与运算。通过构造一个掩码（mask），掩码中对应选取位置为 1，其余位置为 0，然后与原二进制数进行按位与运算。

示例：取二进制数 01101010 的末尾 4 位

def get_last_n_bits(x, n):mask = (1 << n) - 1return x & mask# 示例
x = 0b01101010
n = 4
result = get_last_n_bits(x, n)
print(f"二进制数 {bin(x)} 的末尾 {n} 位是 {bin(result)}")  # 输出：0b1010

思维流程

③ 将指定位设置为 1

原理：使用按位或运算

要将二进制数中的某几位设置为 1，可以使用按位或运算。通过构造一个掩码，掩码中对应选取位置为 1，其余位置为 0，然后与原二进制数进行按位或运算。

**示例：将二进制数 01101010 的末尾 4 位设置为 **1

def set_last_n_bits(x, n):mask = (1 << n) - 1return x | mask# 示例
x = 0b01101010
n = 4
result = set_last_n_bits(x, n)
print(f"二进制数 {bin(x)} 的末尾 {n} 位设置为 1 后是 {bin(result)}")  # 输出：0b1111

④ 反转指定位

原理：使用按位异或运算

要反转二进制数中的某几位，可以使用按位异或运算。通过构造一个掩码，掩码中对应选取位置为 1，其余位置为 0，然后与原二进制数进行按位异或运算。

示例：将二进制数 01101010 的末尾 4 位反转

def invert_last_n_bits(x, n):mask = (1 << n) - 1return x ^ mask# 示例
x = 0b01101010
n = 4
result = invert_last_n_bits(x, n)
print(f"二进制数 {bin(x)} 的末尾 {n} 位反转后是 {bin(result)}")  # 输出：0b1100

⑤ 交换两个数

原理：使用按位异或运算

通过按位异或运算可以实现两个数的交换，而无需额外的变量。

示例：交换 a 和 b 的值

def swap_numbers(a, b):a ^= bb ^= aa ^= breturn a, b# 示例
a, b = 10, 20
a, b = swap_numbers(a, b)
print(f"交换后 a = {a}, b = {b}")  # 输出：a = 20, b = 10

思维流程图

⑥ 将二进制最右侧为 1 的二进位改为 0

**原理：使用 **X & (X - 1)

要将二进制数中最右侧为 1 的二进位改为 0，可以使用 X & (X - 1) 操作。

**示例：将 01101100 最右侧的 1 改为 **0

def clear_rightmost_bit(x):return x & (x - 1)# 示例
x = 0b01101100
result = clear_rightmost_bit(x)
print(f"二进制数 {bin(x)} 最右侧的 1 改为 0 后是 {bin(result)}")  # 输出：0b1101000

⑦ 计算二进制中二进位为 1 的个数

原理：使用 X & (X - 1) 统计次数

通过不断使用 X & (X - 1) 操作，可以将二进制数中最右侧为 1 的二进位改为 0，直到所有位都为 0。统计操作次数，即可得到二进制中 1 的个数。

示例：计算 01101100 中 1 的个数

def count_ones(x):count = 0while x:x &= (x - 1)count += 1return count# 示例
x = 0b01101100
result = count_ones(x)
print(f"二进制数 {bin(x)} 中 1 的个数是 {result}")  # 输出：4

思维流程

⑧ 判断某数是否为 2 的幂次方

**原理：使用 **X & (X - 1) == 0

判断一个数是否为 2 的幂次方，可以通过 X & (X - 1) == 0 来实现。如果结果为 0，则该数是 2 的幂次方；否则，不是。

示例：判断 4 是否为 2 的幂次方

def is_power_of_two(x):return (x & (x - 1)) == 0# 示例
x = 4
result = is_power_of_two(x)
print(f"{x} 是 2 的幂次方吗？ {result}")  # 输出：True

思维流程

2. 位运算的常用操作总结

① 常用操作列表

功能	位运算符	示例
判断整数奇偶	&	(x & 1) == 0
选取指定位	&	x & ((1 << n) - 1)
将指定位设置为 1	`	`
反转指定位	^	x ^ ((1 << n) - 1)
交换两个数	^	a ^= b; b ^= a; a ^= b;
将最右侧 1 改为 0	&	x & (x - 1)
计算 1 的个数	&	while x: x &= (x - 1); count += 1
判断是否为 2 的幂次方	&	(x & (x - 1)) == 0

3. 二进制枚举子集

① 二进制枚举子集简介

子集的概念

子集是指一个集合中的任意元素都是另一个集合的元素。例如，集合 {1, 2, 3} 的子集包括 {}、{1}、{2}、{3}、{1, 2}、{1, 3}、{2, 3}、{1, 2, 3}。

二进制枚举子集的原理

对于一个元素个数为 n 的集合 S，可以用一个长度为 n 的二进制数来表示其子集。每一位对应集合中的一个元素，1 表示选取该元素，0 表示不选取该元素。通过枚举 0 到 2^n - 1 的所有二进制数，可以得到集合 S 的所有子集。

② 二进制枚举子集代码

代码实现：枚举集合 S 的所有子集

def subsets(S):n = len(S)sub_sets = []for i in range(1 << n):sub_set = []for j in range(n):if i & (1 << j):sub_set.append(S[j])sub_sets.append(sub_set)return sub_sets# 示例
S = [1, 2, 3]
result = subsets(S)
print(f"集合 {S} 的所有子集是 {result}")  # 输出：[[], [1], [2], [1, 2], [3], [1, 3], [2, 3], [1, 2, 3]]

思维流程图

Ok，今天我们就学习到这！😎👌

---

相关链接

• 项目地址：LeetCode-CookBook
• 相关文档：专栏地址
• 作者主页：GISer Liu-CSDN博客

如果觉得我的文章对您有帮助，三连+关注便是对我创作的最大鼓励！或者一个star🌟也可以😂.