计算机组成原理 - 2. 数据的表示和运算
整理自天勤高分笔记,购书链接:
24 天勤高分笔记
要记住的几个数字 📓:
215=327682^{15} = 32768215=32768
216=655362^{16} = 65536216=65536
231=21474836482^{31} = 2147483648231=2147483648
232=42949672962^{32} = 4294967296232=4294967296
1010=AH1010 = AH1010=AH
1011=BH1011 = BH1011=BH
1100=CH1100 = CH1100=CH
1101=DH1101 = DH1101=DH
1110=EH1110 = EH1110=EH
1111=FH1111 = FH1111=FH
103≈21010^3 \approx 2^{10}103≈210
106≈22010^6 \approx 2^{20}106≈220
109≈23010^9 \approx 2^{30}109≈230
[10⋯0]补=最小负数[10\cdots0]_补 = 最小负数[10⋯0]补=最小负数
[11⋯1]补=−1[11\cdots1]_补 = -1[11⋯1]补=−1
[1.10⋯0]补=−12[1.10\cdots0]_补 = -\frac{1}{2}[1.10⋯0]补=−21
[1.0⋯0]补=−1[1.0\cdots0]_补 = -1[1.0⋯0]补=−1
无符号: 65535=FFFFH65535 = FFFFH65535=FFFFH
目录
- 数制与编码
- 进位计数制及其相互转换
- BCD 码
- 字符与字符串
- 校验码
- 定点数的表示与运算
- 定点数的表示
- 定点数的移位运算
- 溢出的判别方法
- 定点数的乘法运算
- 定点数的除法运算
- 浮点数的表示与运算
- 浮点数的表示
- 浮点数的加减运算
- 算术逻辑单元 ALU
- 串行加法器和并行加法器
- 算术逻辑单元的功能和结构
数制与编码
进位计数制及其相互转换
① 十进制转换为二进制
🌰 例: 将 19.687510{19.6875}_{10}19.687510 转换为二进制数
❶ 整数部分
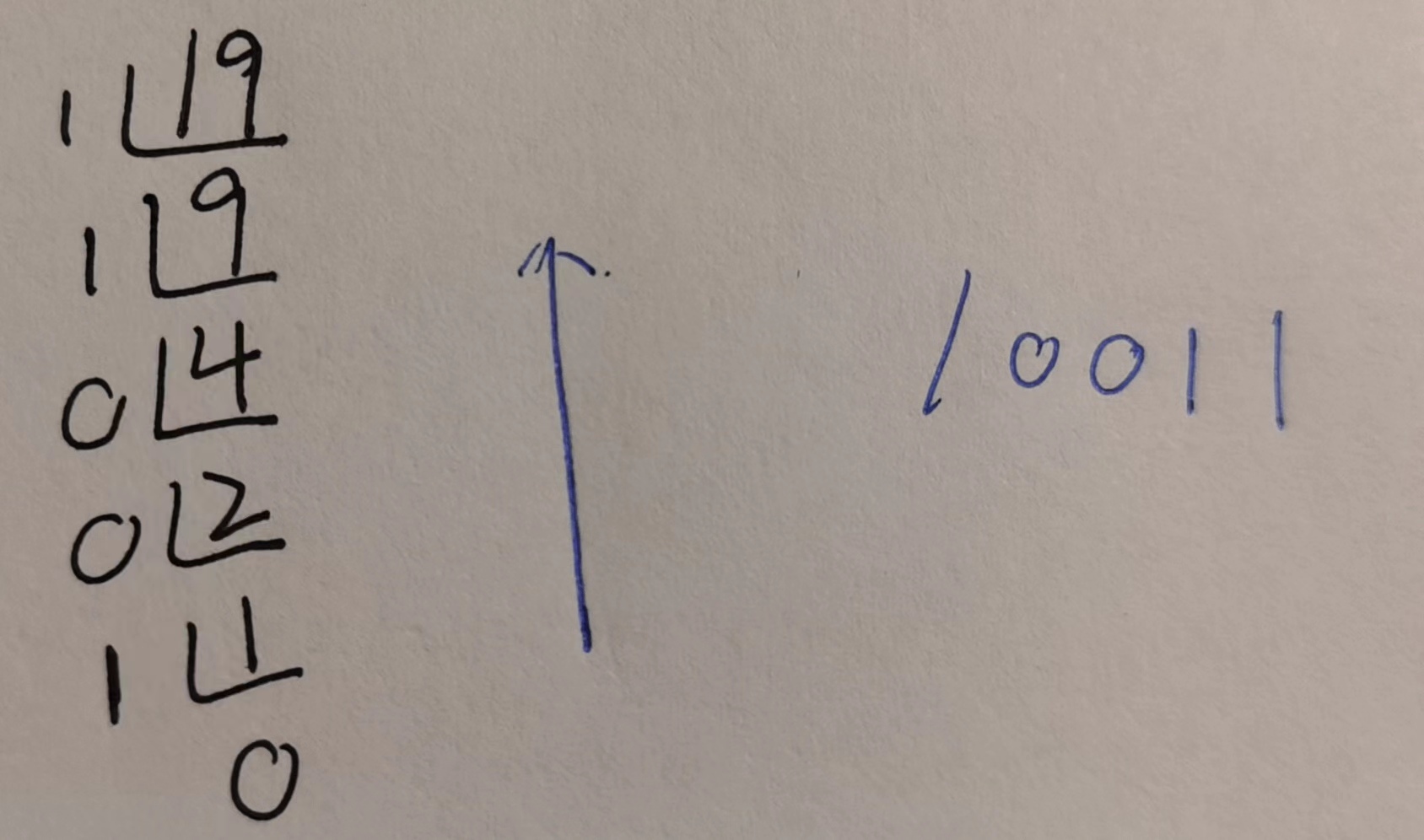
❷ 小数部分
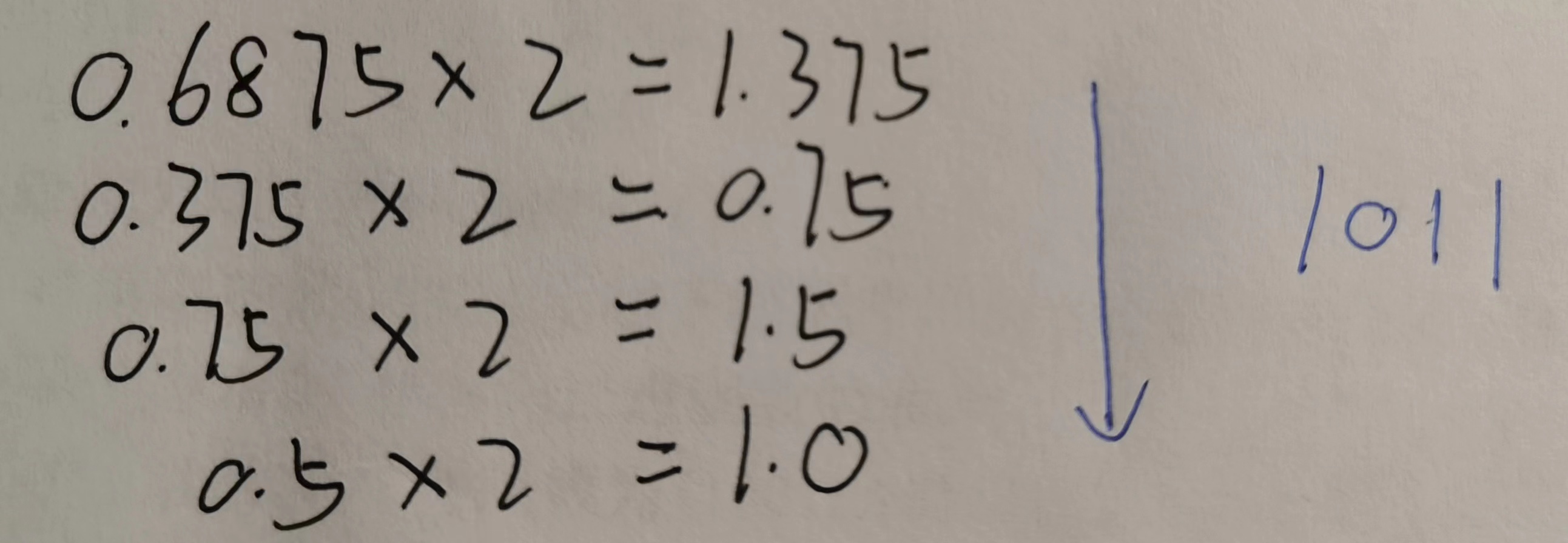
19.687510=10011.10112{19.6875}_{10} = {10011.1011}_219.687510=10011.10112
注意 🔔 :
不是所有十进制小数都可用二进制表示,如 0.20.20.2
② 二进制数转换为八进制数、十六进制数
🌰 例: 将二进制数 1101011110012{110101111001}_21101011110012 分别转换为八进制数和十六进制数
从最低有效位 (LSD) 开始,3 位一划分,组成八进制数;4 位一划分,组成十六进制数。高位不足用 0 来补齐。
1101011110012=6571Q=D79H{110101111001}_2 = 6571Q = D79H1101011110012=6571Q=D79H
③ 计算机内部为什么使用二进制编码❓️
❶ 基本符号少(“0” 和 “1”) 易于用 稳态电路 实现;
❷ 编码、计数、运算等的 规则 简单;
❸ 和 逻辑命题 “真” 和 “假” 的对应关系简单;
BCD 码
二进制编码的十进制数 (Binary-Coded Decimal, BCD) 是以二进制数来编码表示十进制的 0~9
⮚ 8421 BCD 码,位权一致
❶ 用四位二进制数来表示一位十进制的 ‘0’ ~ ‘9’,其二进制数每位的权重由高到低分别是 8、4、2、1 。
❷ 再用十六进制的 C 表示 ‘+’ 号,十六进制数 D 表示 ‘-’ 号,且均放在数字串的最后。
❸ 当十进制数的位数为偶数时,在第一个字节的高 4 位补 “0” 。
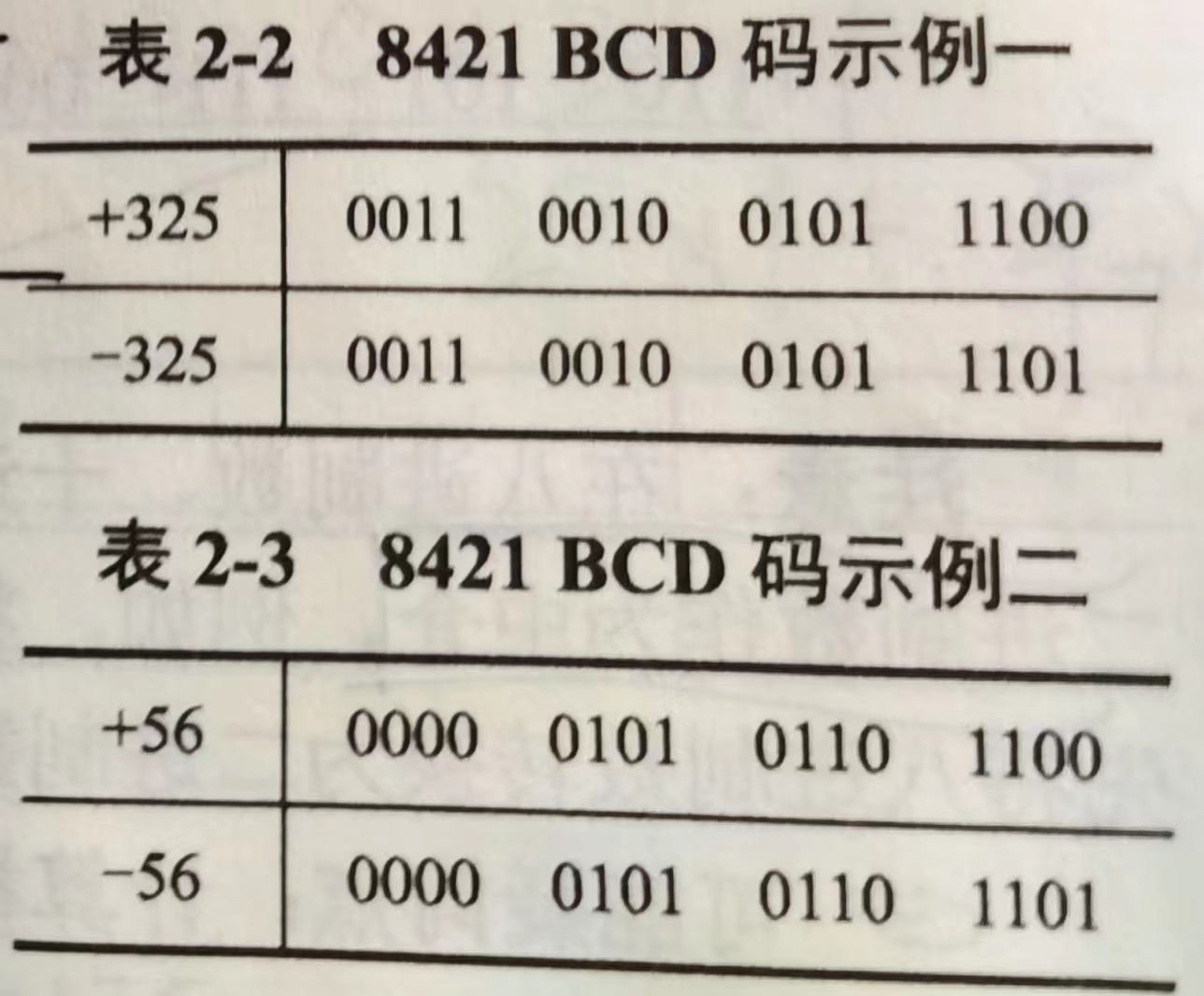
注意 🔔 :
8421 BCD 码遇到 1001 就产生进位。
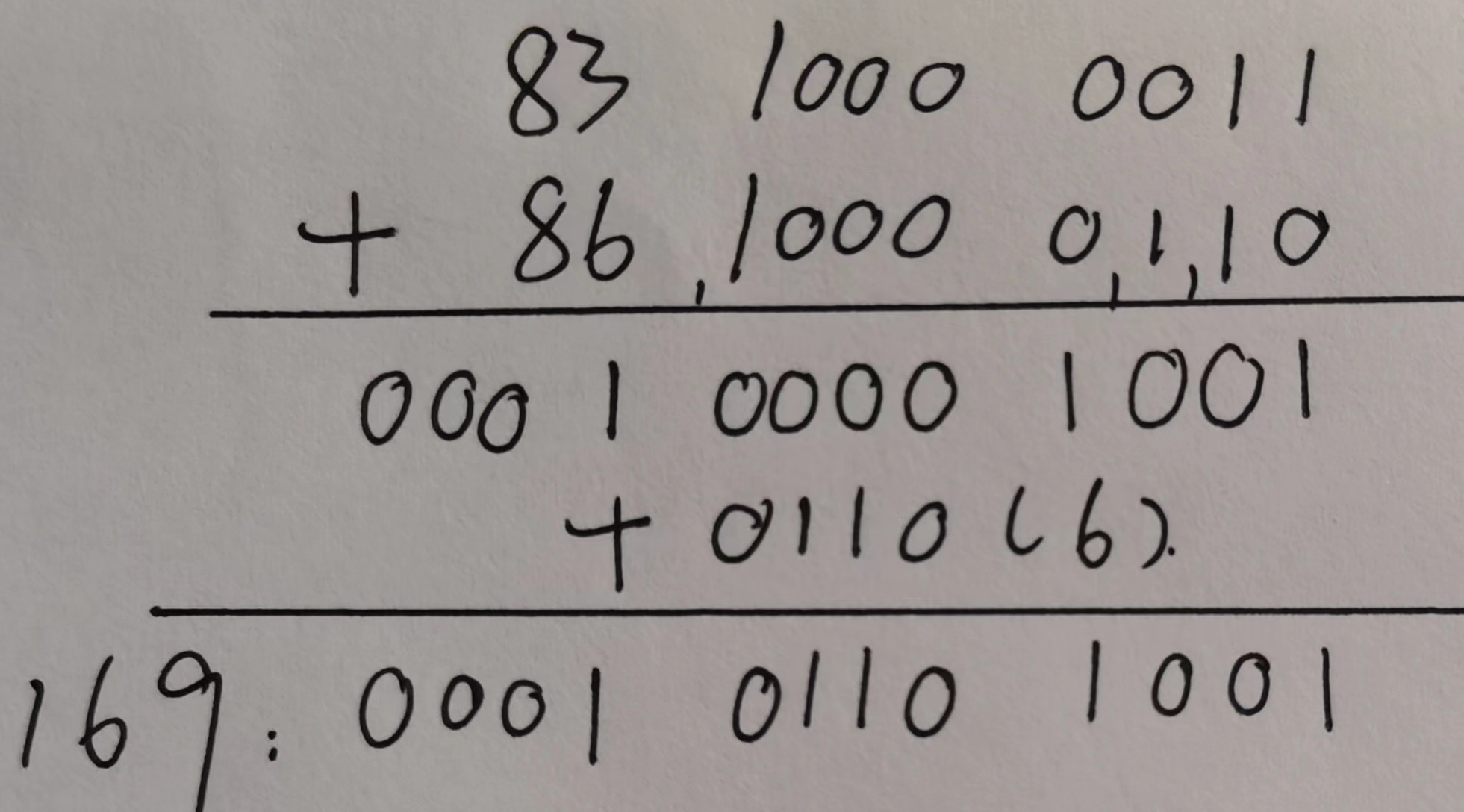
字符与字符串
① 字符编码 ASCII 码
128 个字符,96 个可打印字符,32 个控制字符。
几个需要记住的 ASCII 码📓:
0 : 48
A : 65
a : 97
7 位编码,但计算机仍用 1 个字节来存放一个 ASCII 字符,最高位通常保持为 0(在 数据传输 时可用作 奇偶校验位)。
② 汉字编码
汉字编码主要包括汉字的输入编码、汉字内码和汉字字形码三种
❶ 区位码 用两个字节表示一个汉字(每个字节对应 2 个 16 进制数),将汉字和图形符号排列在一个 94 行 94 列的二维代码表中。
❷ 国标码是将十进制的区位码 转换为十六进制后,再在每个字节加上 20 H,即加上 2020 H。
❸ 国标码 = (区位码)16{(区位码)}_{16}(区位码)16 + 2020H
汉字内码 = (国标码)16{(国标码)}_{16}(国标码)16 + 8080H
③ 字符串大小端存放
🌰 例 1: 某计算机字长为 32 位,按字节编址,采用 小端 (Little Endian) 方式存放数据。假定有一个 double 型变量,其机器数表示为 1122 3344 5566 7788H,存放在 0000 8040H 开始的连续存储单元中,则存储单元 0000 8046H 中存放的是 22H
解析:
❶ 按字节编址,2 个 16 进制数 = 1 个字节
❷ 小端 (低字节存放低地址)

🌰 例 2: 某计算机采用大端方式,按字节编址。某指令中操作数的机器数为 1234 FF00H,该操作数采用基址寻址方式,形式地址(用补码表示)为 FF12H, 基址寄存器的内容为 FF12H, 基址寄存器的内容为 F000 0000H,则该操作数的 LSB (最低有效字节) 所在的地址是 EFFFFF15H
解析:
❶ 地址 为 无符号数,相对/形式地址/位移量 用 补码 表示
(FF12H)补=(1111111100010010)补=(1000000011101110)原=−EEH{(FF12H)}_补= (1111 1111 0001 0010)_补 = (1000000011101110)_原 = -EEH(FF12H)补=(1111111100010010)补=(1000000011101110)原=−EEH
F0000000H−EEH=EFFFFF12HF0000000H - EEH = EFFFFF12HF0000000H−EEH=EFFFFF12H
❷ 2 个 16 进制数 = 1 个字节,操作数共 4 字节
大端(低字节高地址)
EFFFFF12H+(4−1)=EFFFFF15HEFFFFF12H + (4 - 1) = EFFFFF15HEFFFFF12H+(4−1)=EFFFFF15H
校验码
① 奇偶校验码
❶ 奇校验:添加一位校验码后,使得整个码字里面 1 的个数是奇数。
❷ 偶校验:添加一位校验码后,使得整个码字里面 1 的个数是偶数。
😟 缺陷:检查不出偶数位错
② 循环冗余校验码 (CRC) 码
M(x) 为发送信息的多项式,G(x) 为生成多项式,代表校验位信息。
设 M(x)=x3+1;M(x) = x^3 + 1;M(x)=x3+1; G(x)=x3+x+1G(x) = x^3 + x + 1G(x)=x3+x+1
❶ 写出 M(x) 和 G(x) 所代表的二进制码
M(x) = 1001 G(x) = 1011
❷ 将 M(x) 所代表的二进制码左移 G(x) 的 最高位数, 这里是左移 3 位,得到 1001000
❸ 模 2 除法:
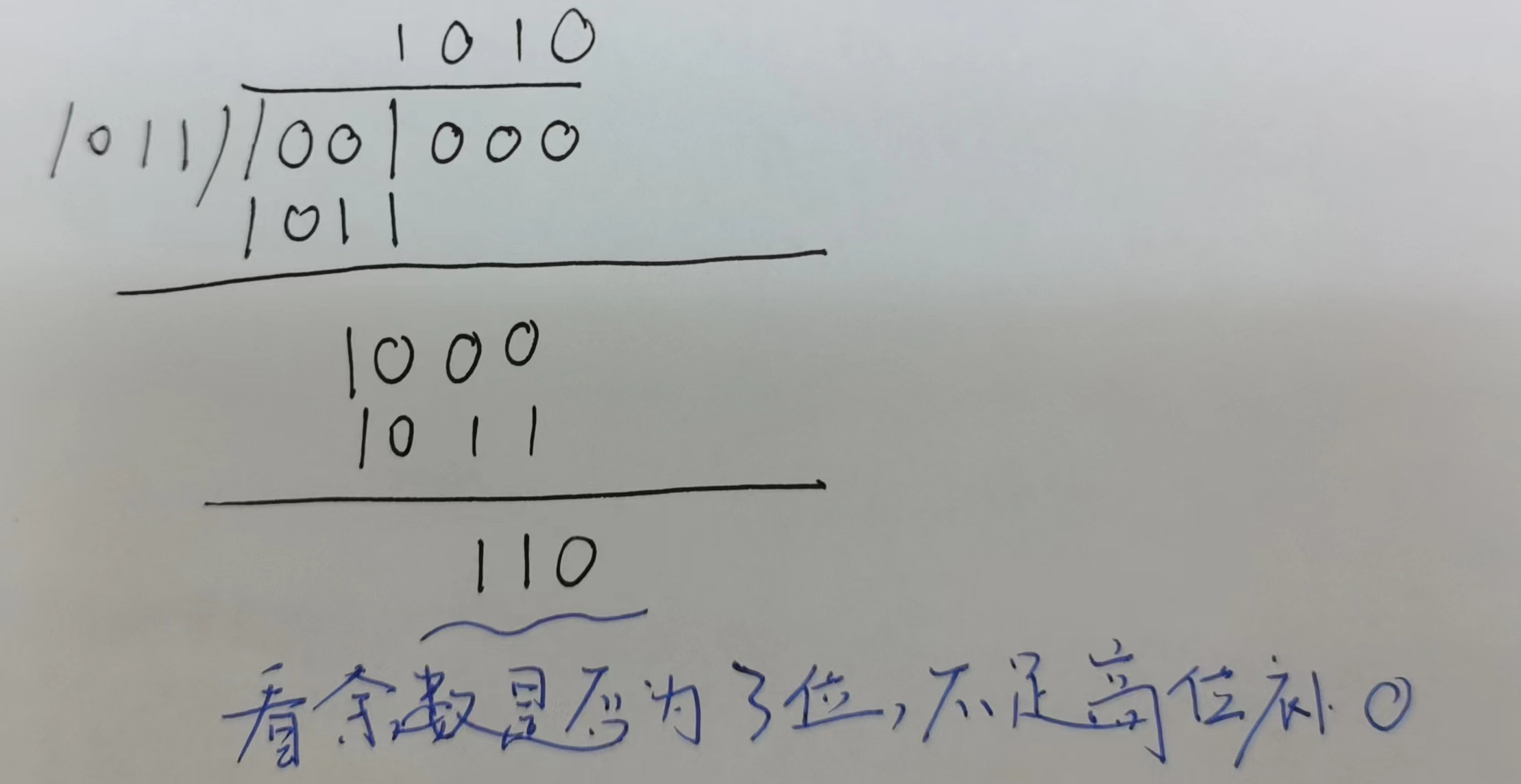
❹ 将 M(x) 与余数 110 合并得到 1001110 即为循环冗余校验码
循环冗余校验码进行检错的重要特性⭐️:
❶ 具有 r 检测位的多项式能够检测出所有小于或等于 r 的突发错误
❷ 长度大于 r + 1 的错误逃脱的概率为 12r\frac{1}{2^r}2r1
③ 海明码
假设要推导 D=101101D = 101101D=101101 这串二进制数的海明码
❶ 确定校验位的位数 rrr
数据的位数 k=6k = 6k=6
2r−1⩾k+r2^r -1 \geqslant k + r2r−1⩾k+r
r=4r = 4r=4
❷ 校验位 P1P_1P1、P2P_2P2、P3P_3P3、P4P_4P4 分别位于 M1M_1M1、M2M_2M2、M4M_4M4、M8M_8M8
❸ 用下表计算出 P1P_1P1、P2P_2P2、P3P_3P3、P4P_4P4

海明码即为 1011100100。
❹ 海明码的校验
假设 M5M_5M5 即 D2D_2D2 出错:
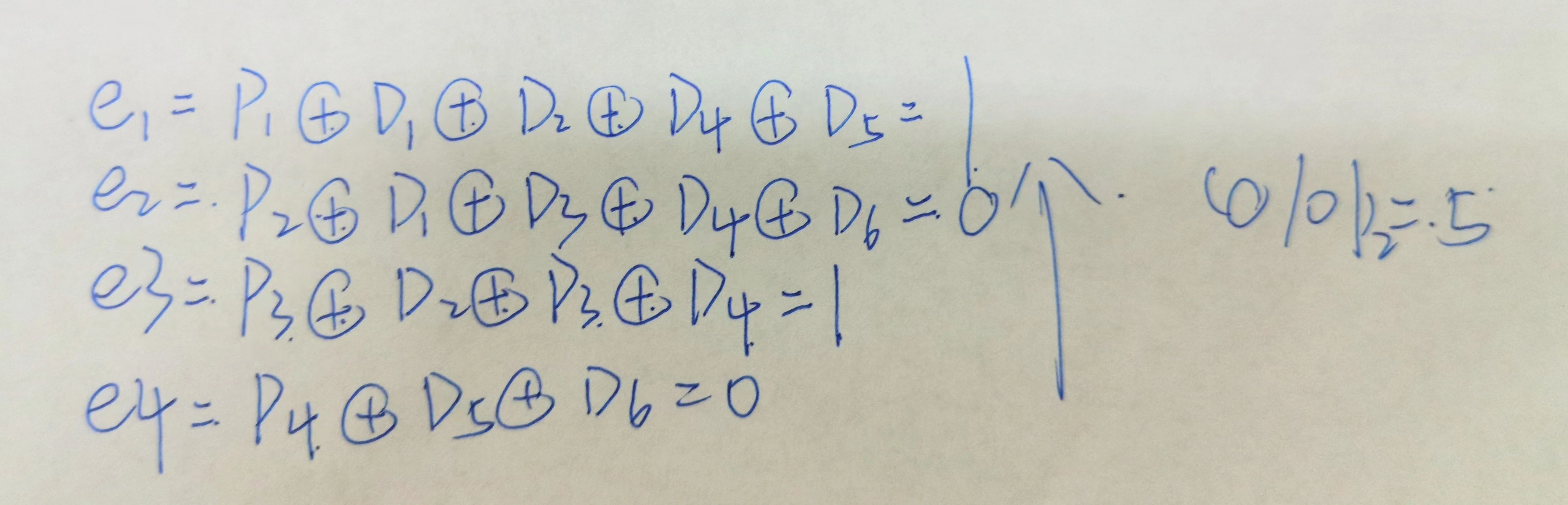
定点数的表示与运算
定点数的表示
① 真值和机器数
真值是机器数所代表的实际的值,机器数是真值在计算机中的表示。
② 无符号数的表示
一般在全部都是正数运算且结果不出现负值的场合下,可以省略符号位,使用无符号数表示。例如,在进行 地址运算 时可用无符号数。
若机器字长为 8 位,则数的表示范围为 0∼(28−1)0 \sim (2^8 - 1)0∼(28−1)
1 个需要记住的无符号数表示📓:
65535 = FFFFH
🌰 例:
有如下 C 语言语句:
unsigned short x = 65530;unsigned int y = x;
得到 y 的机器数为: 0000FFFAH
65535 = FFFFH 65530 = FFFAH
无符号整数 0 扩展 , 所以 y 的机器数为 0000FFFAH
③ 有符号数的表示 (原码、补码、反码、移码)
❶ 3 种机器数最高位均为符号位。符号位和数值部分可用 “.”(小数) 或 “,”(整数) 隔开。
❷ 真值为正数时,原码、补码、反码 表示形式相同,即符号位为 “0”,数值部分与真值相同。
❸ 真值为负数时,符号位为 “1”,补码为原码的 “最右边的 1 及其右边的 0 不变,其余数值位取反”,
反码为原码的 “所有数值位取反”。
❹ 移码就是补码的符号位取反。
🌰 例:
ⓐ x=−0.0110x = -0.0110x=−0.0110
[x]原=1.0110[x]_{原} = 1.0110[x]原=1.0110 [x]补=1.1010[x]_{补} = 1.1010[x]补=1.1010 [x]反=1.1001[x]_{反} = 1.1001[x]反=1.1001 [x]移=0.1010[x]_{移} = 0.1010[x]移=0.1010
ⓑ [−0.0000]补=[1.1111]+1=[0.0000][-0.0000]_{补} = [1.1111] + 1 = [0.0000][−0.0000]补=[1.1111]+1=[0.0000] (最高符号的进位舍去)
❺ 0 的原码和反码都有两种,补码只有唯一一种

❻ 补码可以比原码和反码多表示一个最小负数
对于定点整数来说:

对于定点小数来说,补码也应该比原码和反码多表示一个数,这个数就是 -1。
🌰 例:
假设机器字长为 16 位,用定点补码小数表示时,一个字所能表示的范围是 −1∼(1−2−15)-1 \sim (1 - 2^{-15})−1∼(1−2−15)
❼ 已知 [x]补[x]_补[x]补 求 [−x]补[-x]_补[−x]补
连同符号位在内每位取反,末位加 1,即可得 [−x]补[-x]_补[−x]补
🌰 例:
[x]补=1.0010010[x]_补 = 1.0010010[x]补=1.0010010 [−x]补=0.1101101+1=0.1101110[-x]_补 = 0.1101101 +1 = 0.1101110[−x]补=0.1101101+1=0.1101110
❽ 移码
补码的缺点😟 :无法直接比较大小
移码:在补码的基础上加上 2n−12^{n-1}2n−1 就是移码,表示范围为 0∼(2n−1)0 \sim (2^{n} - 1)0∼(2n−1)
🌰 例:
十进制数 −0.3125-0.3125−0.3125 的 888 位移码编码为 0.1011000=58H0.1011000 = 58H0.1011000=58H
[−0.3125]原=1.0101[-0.3125]_原 = 1.0101[−0.3125]原=1.0101
[−0.3125]补=1.1011[-0.3125]_补 = 1.1011[−0.3125]补=1.1011
[−0.3125]移=0.1011000[-0.3125]_移 = 0.1011000[−0.3125]移=0.1011000 (低位补 0)
❾ ⭐️ 为什么现代计算机都使用补码来表示机器数 ❓️
➤ 0 的补码只有一种
➤ 符号位作为代码可以和数值位一起参与运算
➤ 减法可以转换为加法
➤ 对负数补码进行扩充可以直接补符号位
➤ 可以多表示一个最小负数
❿ ⭐️ 补码性质总结:
➤ 无论机器字长为多少,-1 的补码永远是全 1
➤ 最小负数的补码永远是首位为 1,后面为全 0。如
[10000000]补=−128[10000000]_补 = -128[10000000]补=−128
[1000000000000000]补=−32768[1000000000000000]_补 = -32768[1000000000000000]补=−32768
🌰 例 1:
有如下 C 语言程序段:
short si = -32767;unsigned short usi = si;
执行完上面两条语句, usi 的值为:32769
[1000000000000000]补=−32768[1000000000000000]_补 = -32768[1000000000000000]补=−32768
[1000000000000001]补=−32767[1000000000000001]_补 = -32767[1000000000000001]补=−32767
usi=215+1=32768+1=32769usi = 2^{15} + 1 = 32768 + 1 = 32769usi=215+1=32768+1=32769
🌰 例 2:
有如下 C 语言程序段:
unsigned short usi = 65535;short si = usi;
执行完上面两条语句,si 的值为:-1
无符号整数 65535 = 2162^{16}216 - 1 的机器数为 1111 1111 1111 1111
转换为有符号数,补码全 1 真值为 -1
⓫ 当使用补码表示时,如果符号位相同,则数值位越大,真值越大
🌰 例:
ⓐ 设 xxx 为整数,[x]补=1,x1x2x3x4x5[x]_补 = 1,x_1x_2x_3x_4x_5[x]补=1,x1x2x3x4x5,若要 x<−16x < -16x<−16,x1∼x5x_1 \sim x_5x1∼x5 应满足的条件是 x1x_1x1 必须为 0,x2∼x5x_2 \sim x_5x2∼x5 任意。
−16=1,10000-16 = 1,10000−16=1,10000
ⓑ [x]补=1.x1x2x3x4[x]_补 = 1.x_1x_2x_3x_4[x]补=1.x1x2x3x4,当满足 x1=1x_1 = 1x1=1,x2∼x4x_2 \sim x_4x2∼x4 至少有一个为 1, x>−12x > -\frac{1}{2}x>−21 成立。
−12=1.1000-\frac{1}{2} = 1.1000−21=1.1000
ⓒ 由 3 个 “1” 和 5 个 “0” 组成的八位二进制补码,能表示的最小整数是
10000011=−12510000011 = -12510000011=−125
定点数的移位运算
① 逻辑移位:左移右移都补 0
② 算术移位:
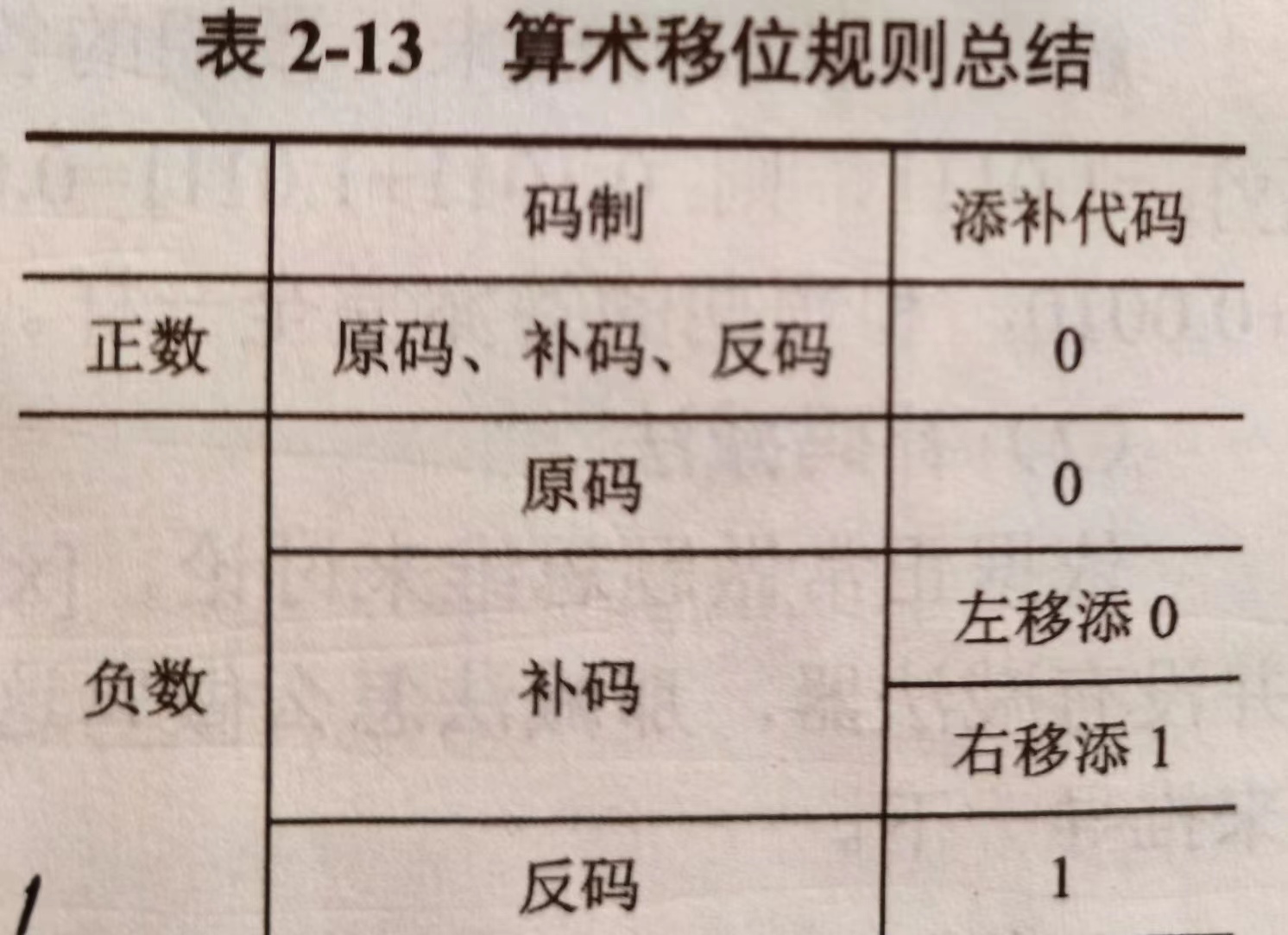
溢出的判别方法
两数相加产生了溢出,数值位就需要扩充。也就是说,数值位 “跑” 到符号位去了,于是就改变了符号的性质,产生了与预期不一样的结果。
溢出的 根本原因:运算结果无法表示
⭐️ 计算机是怎么判断溢出的呢❓️
① 若 实际参加运算的两个数 符号位相同,结果又与原符号数的符号不同,即认为溢出。
② 若数值位最高位相加无进位,而 符号位相加有进位,则有溢出。
③ 变形补码(两位符号位): 两位符号位不同,则溢出。(高位符号位永远代表真正的符号位)
定点数的乘法运算
① 原码 1 位乘

注意 🔔 :
❶ 两个 nnn 位数相乘,共需要进行 nnn 次加法运算和 nnn 次移位操作。
❷ 所有移位均为 逻辑移位。
❸ 由于在部分积相加中,可能导致两个小数相加大于 1, 因此 部分积一般使用 n+1n + 1n+1 位寄存器。
② 补码 1 位乘 : 校正法 ⭐️
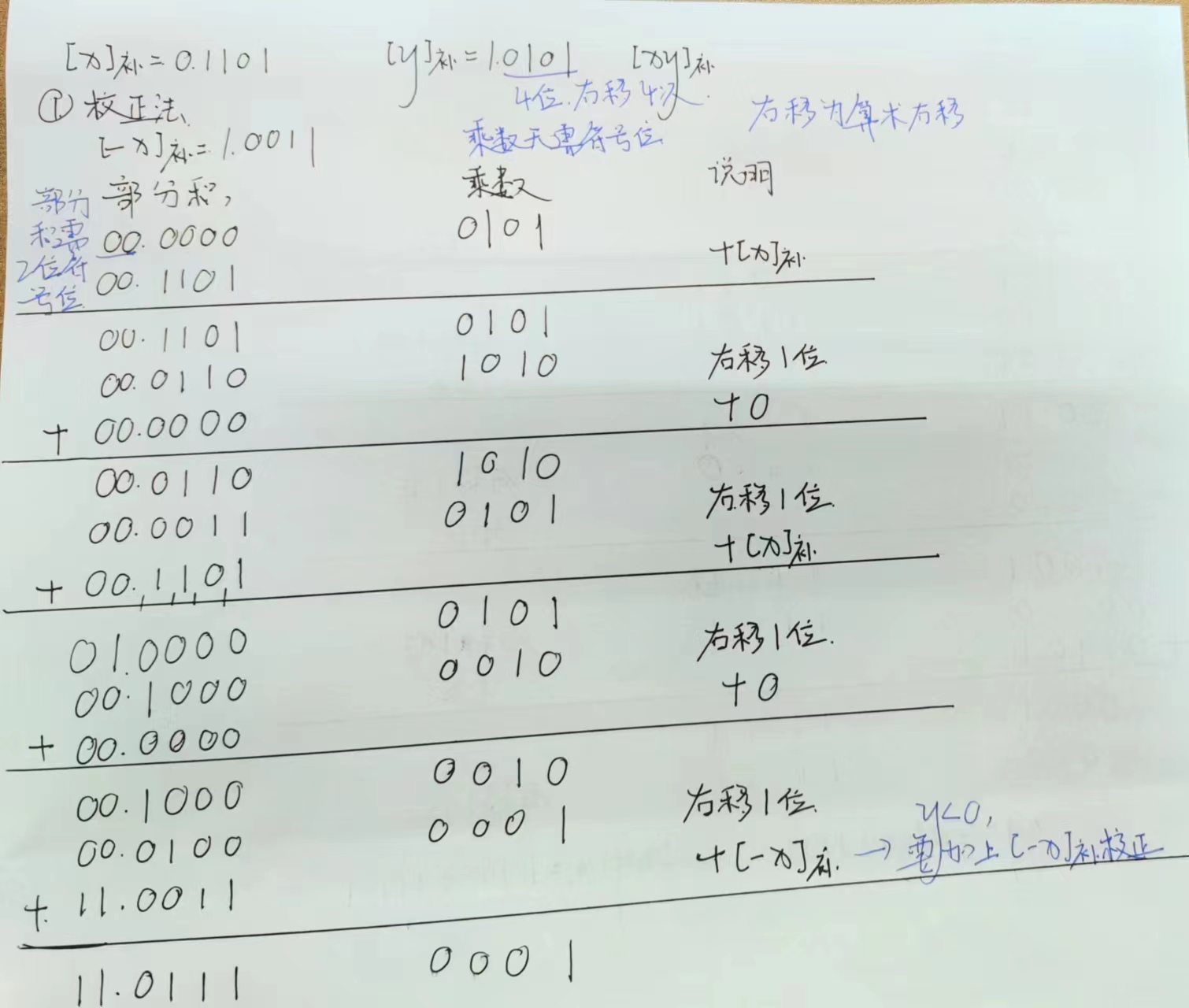
③ 补码 1 位乘:比较法 ⭐️ ⭐️
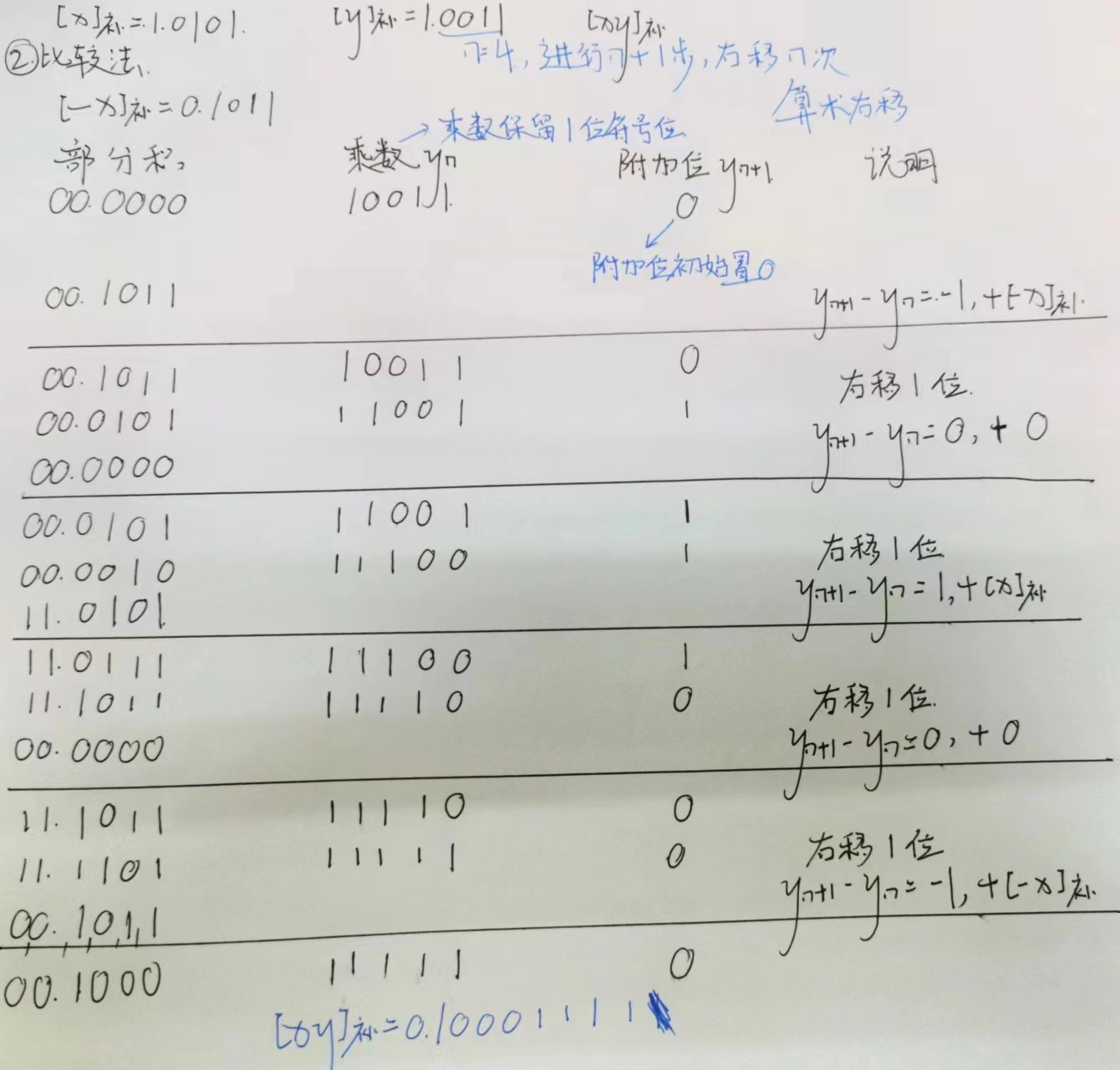
定点数的除法运算
nnn 位小数除法共上商 n+1n + 1n+1 次,且共移位 nnn 次。 ⭐️
① 原码恢复余数法

② 原码加减交替法⭐️

③ 补码加减交替法⭐️⭐️

⑤ 原码除法 和 补码除法 判断溢出的方法:
❶ 原码除法以第一次上商的商值来判断是否溢出,若第一次上商 1,则为溢出;
❷ 补码除法以第一次上商的商值(即商的符号位)与两个操作数符号位 异或 的结果进行比较,若比较结果不同,则为溢出。
⑥ 原码 和 补码 在 加减交替法 的过程中有何 相同 和 不同 之处❓️⭐️⭐️
🙆♂️ 相同:形成新余数的规则相同
🙅♂️ 不同:
❶ 商符的形成不同:
原码 除法的商符有两数符号位通过 “异或” 运算获得
补码 除法的商符在求商值的过程中 自然形成
❷ 参与运算的数不同:
原码 除法参与运算的数是 绝对值的补码
补码 除法参与运算的数是 补码
❸ 上商的规则不同:
原码 除法,余数 正 上商 1,余数 负 上商 0
补码 除法,余数与除数 同号 上商 1,余数与除数 异号 上商 0
❹ 第一步操作不同:
原码 除法第一步进行被除数 减 除数的操作
补码 除法第一步要根据被除数与除数的 符号决定 做加法还是减法(同号做减法,异号做加法)
⑦ 计算机内部如何实现填充(扩展)操作❓️
对于 无符号整数,只要在 高位补 0,进行 “零扩展”
对于 有符号数,可能有两种情况:
❶ 对于定点 整数,在符号位后的数值高位进行
ⓐ 原码:符号位不变,数值部分高位补 0
ⓑ 补码:高位直接补符号,称为 “符号扩展” 方式
❷ 对于定点 小数,直接在 低位补 0 即可
浮点数的表示与运算
浮点数的表示
IEEE 754 标准⭐️⭐️

尾数用原码表示,阶码用移码表示
Q1: 为什么阶码用移码表示❓️
因为在浮点数的加减运算中,要进行对阶操作,所以需要比较两个阶的大小,移码表示的实质就是把阶加上一个偏置常数,使得所有数的阶码都是一个正整数,比较大小时,只要按高位到低位的顺序比较就行了,因而引入移码可以 简化阶的比较过程。
Q2: IEEE 754 如何表示 0 和 ∞\infty∞❓️
❶ 当 阶码 E 为全 0 且尾数 M 也为全 0 时,表示 真值为 0,结合符号位 S 为 0 或 1,有正零和负零之分(0000 0000H 表示 +0, 8000 0000H 表示 -0)。
❷ 当 阶码 E 为全 1 且尾数 M 为全 0 时,表示 真值为 ∞\infty∞, 结合符号位 S 为 0 或 1,有 +∞+\infty+∞ 和 −∞-\infty−∞ 之分(7F80 0000H 表示 +∞+\infty+∞, FF80 0000H 表示 −∞-\infty−∞)。
🌰 例: ⭐️
ⓐ 若浮点数 x 的 IEEE 754 标准存储格式为 41360000H, 试求其浮点数的十进制数值 11.375
010000010011011000000000000000000\ 10000010\ 011011000000000000000000 10000010 01101100000000000000000
E=10000010=130E = 10000010 = 130E=10000010=130 e=130−127=3e = 130 - 127 = 3e=130−127=3
1.M=1.0110111.M = 1.0110111.M=1.011011
x=(−1)0×1.011011×23=1011.0112=11.375x = (-1)^0 \times 1.011011 \times 2^3 = 1011.011_2 = 11.375x=(−1)0×1.011011×23=1011.0112=11.375
ⓑ 浮点数 261.6 的 IEEE 754 标准存储格式为 4382CCCCH4382\ CCCCH4382 CCCCH
261.6=100000101.1001...=1.00000101100110011001100×28261.6 = 100000101.1001 ... = 1.00000101100110011001100 \times 2^{8}261.6=100000101.1001...=1.00000101100110011001100×28
1.M=1.000001011001100110011001.M = 1.000001011001100110011001.M=1.00000101100110011001100
E=e+127=8+127=135=10000111E = e + 127 = 8 + 127 = 135 = 10000111E=e+127=8+127=135=10000111
01000011100000101100110011001100=4382CCCCH0\ 10000111\ 00000101100110011001100 = 4382\ CCCCH0 10000111 00000101100110011001100=4382 CCCCH
注意 🔔 :
float 型 / IEEE 754 标准中的单精度浮点数格式 所能表示的:
❶ 最小正数:2−1262^{-126}2−126
尾数 1.0⋯0=11.0\cdots0 = 11.0⋯0=1 阶码 E=00000001=1E = 00000001 = 1E=00000001=1
e=1−127=−126e = 1 - 127 = -126e=1−127=−126
1×2−126=2−1261 \times 2^{-126} = 2^{-126}1×2−126=2−126
❷ 最大正数:2128−21042^{128}-2^{104}2128−2104
尾数 1.1⋯1=2−2−231.1\cdots1 = 2 - 2^{-23}1.1⋯1=2−2−23 阶码 E=11111110=254E = 11111110 = 254E=11111110=254
e=254−127=127e = 254 - 127 = 127e=254−127=127
(2−2−23)×2127=2128−2104(2 - 2^{-23}) \times 2^{127} = 2^{128} - 2^{104}(2−2−23)×2127=2128−2104
浮点数的加减运算
① 规格化数:
❶ 补码:数符与小数点后第一位数字相异
❷ 原码:尾数第 1 数位为 1
② 补码规格化
❶ 当尾数出现 01.⋯01.\ \cdots01. ⋯ 或 10.⋯10.\ \cdots10. ⋯, 需右规 1 次,即尾数右移 1 位,阶码 + 1
❷ 当尾数出现 00.0⋯00.0\ \cdots00.0 ⋯ 或 11.1⋯11.1\ \cdots11.1 ⋯ , 需左规 N 次 (N 不固定), 尾数每左移 1 位,阶码 -1,直到尾数呈现规格化形式为止
注意 🔔 :
㊀ 定点 运算发生溢出,必须发出 出错信息❌ 进行中断处理
㊁ 浮点 运算
尾数 溢出,右规
阶码 溢出,上溢,中断 处理;下溢,按 机器 0 处理。
🌰 例: ⭐️⭐️
ⓐ 已知十进制数 x=−5256,y=+591024x = -\frac{5}{256}, y = +\frac{59}{1024}x=−2565,y=+102459,按机器补码浮点数运算规则计算 x−yx - yx−y,结果用二进制表示。其中,浮点数格式如下,数的阶符取 2 位,阶码取 3 位,数符取 2 位,尾数取 9 位。
x=11,011×2−8=11.011×2−5=11.011×211,011x = 11,011 \times 2^{-8} = 11.011 \times 2^{-5} = 11.011 \times 2^{11,011}x=11,011×2−8=11.011×2−5=11.011×211,011
[x]补=11,011;11.011000000[x]_{补} = 11, 011; 11.011000000[x]补=11,011;11.011000000
y=00,111011×2−10=00.111011×2−4=00.111011×211,100y = 00, 111011 \times 2^{-10} = 00.111011 \times 2^{-4} = 00.111011 \times 2^{11, 100}y=00,111011×2−10=00.111011×2−4=00.111011×211,100
[y]补=11,100;00.111011000[y]_{补} = 11, 100; 00.111011000[y]补=11,100;00.111011000
① 对阶
[jx]补=11,011[j_x]_补 = 11, 011[jx]补=11,011 [jy]补=11,100[j_y]_补 = 11, 100[jy]补=11,100 [−jy]补=00,100[-j_y]_补 = 00, 100[−jy]补=00,100
[△j]补=11,111=−1[\triangle j]_补 = 11, 111 = -1[△j]补=11,111=−1
xxx 向 yyy 对齐,xxx 尾数右移 111 位,阶码 +1+ 1+1
[x]补=11,100;11.101100000[x]_{补} = 11, 100; 11.101100000[x]补=11,100;11.101100000
② 尾数求差
yyy 尾数的负数补码 11.00010100011.00010100011.000101000
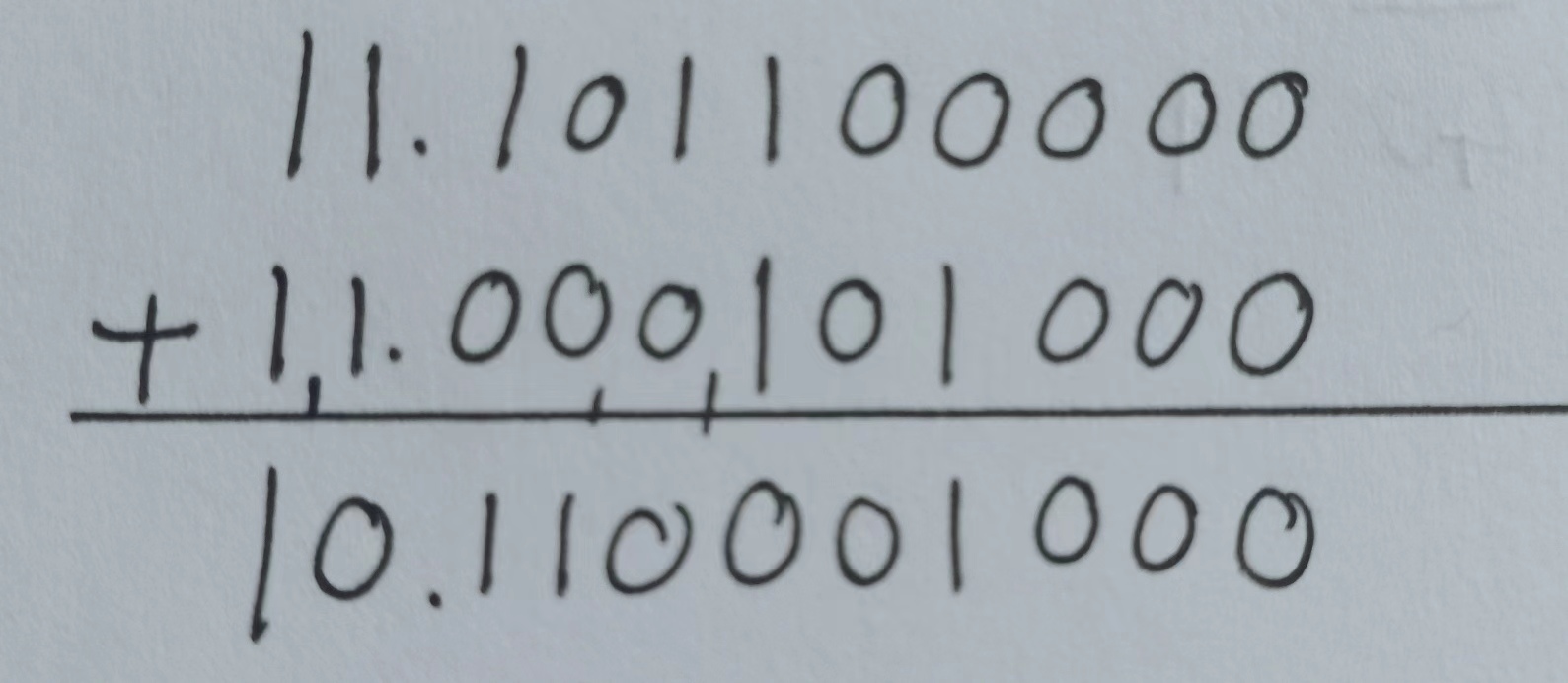
[x+y]补=11,100;10.110001000[x + y]_{补} = 11, 100; 10.110001000[x+y]补=11,100;10.110001000
③ 规格化
尾数右移 1 位,阶码 + 1
[x+y]补=11,101;11.0110001000‾[x + y]_{补} = 11, 101; 11.011000100\underline0[x+y]补=11,101;11.0110001000
④ 舍入处理 (0 舍 1 入)
舍去 0
[x+y]补=11,101;11.011000100[x + y]_{补} = 11, 101; 11.011000100[x+y]补=11,101;11.011000100
⑤ 溢出判断
阶符 111111, 未溢出
ⓑ 设浮点数的阶码和尾数均采用补码表示,且位数分别为 5 位 和 7 位(均含两位符号位)。x=27×29/32x = 2^7 \times 29 / 32x=27×29/32, y=25×5/8y = 2^5 \times 5 / 8y=25×5/8, 求 x+yx + yx+y (结果正溢)
x=29×22=00,11101×22=00.11101×27=00.11101×200,111x = 29 \times 2^2 = 00, 11101 \times 2^2 = 00.11101 \times2^7 = 00.11101 \times2^{00,111}x=29×22=00,11101×22=00.11101×27=00.11101×200,111
[x]补=00,111;00.11101[x]_补 = 00, 111; 00.11101[x]补=00,111;00.11101
y=5×22=00,101×22=00.101×25=00.101×200,101y = 5 \times 2^2 = 00,101\times2^2 = 00.101 \times 2^5 = 00.101 \times 2^{00, 101}y=5×22=00,101×22=00.101×25=00.101×200,101
[y]补=00,101;00.10100[y]_补 = 00,101;00.10100[y]补=00,101;00.10100
① 对阶
yyy 向 xxx 对齐, yyy 尾数右移 222 位,阶码 +2+ 2+2
[y]补=00,111;00.00101[y]_补 = 00,111;00.00101[y]补=00,111;00.00101
② 尾数求和
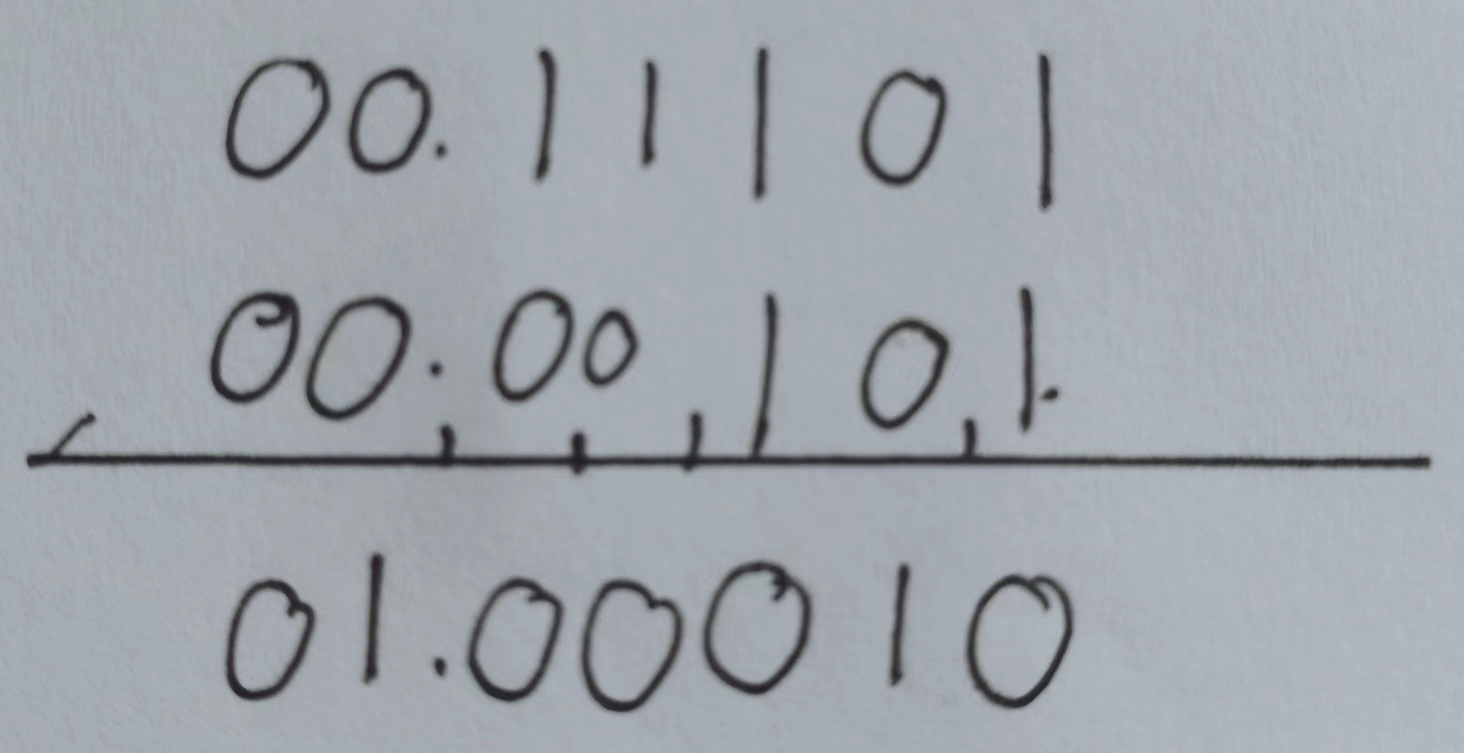
[x+y]补=00,111;01.00010[x + y]_补 = 00,111;01.00010[x+y]补=00,111;01.00010
③ 规格化
尾数右移 111 位,阶码 +1+1+1
[x+y]补=01,000;00.100010‾[x + y]_补 = 01,000;00.10001\underline0[x+y]补=01,000;00.100010
④ 舍入处理 (0 舍 1 入)
舍去 0
[x+y]补=01,000;00.10001[x + y]_补 = 01,000;00.10001[x+y]补=01,000;00.10001
⑤ 溢出判断
阶符 010101, 上溢,中断处理
ⓒ 在 C 语言程序中,以下程序段最终 fff 的值为 0
float f = 2.5 + 1e10;f = f - 1e10;
1e10=1010=10×109≈10×230≈2331e10 = 10^{10} = 10 \times 10^9 \approx 10 \times 2^{30} \approx2^{33}1e10=1010=10×109≈10×230≈233
2.5≈212.5\approx2^12.5≈21
2.52.52.5 的尾数右移 323232 位,使 242424 位有效数字全部丢失,尾数变为全 000
floatf=2.5+1e10=1e10;f=f−1e10=0;float\ f = 2.5 + 1e10 = 1e10;\ \ \ f= f-1e10=0;float f=2.5+1e10=1e10; f=f−1e10=0;
ⓓ 在 C 语言程序中,下列表达式为 true 的有 β\betaβ、γ\gammaγ
α\alphaα. 123456789 == (int)(float)123456789
β\betaβ. 123456 == (int)(float)123456
γ\gammaγ. 123456789 == (int)(double)123456789
⭐️⭐️ float 7 位十进制数
double 17 位十进制数
ⓔ 假定用 111 个 float 类型的变量 xxx 来表示 0.10.10.1,则 ∣x−0.1∣|x - 0.1|∣x−0.1∣ 的值是❓️
0.1=0.00011001100110011001100110011⋯0.1 = 0.000110011001100110011001100\ 11\cdots0.1=0.000110011001100110011001100 11⋯
float 类型有效数字 24 位,∣x−0.1∣=0.0⋯011=110×2−30≈6×10−9|x - 0.1| = 0.0\cdots011 =110 \times 2^{-30} \approx 6 \times10^{-9}∣x−0.1∣=0.0⋯011=110×2−30≈6×10−9
ⓕ ⭐️⭐️已知 f(n)=∑i=0n2i=2n+1−1=11⋯11Bf(n)=\sum_{i=0}^n 2^i = 2^{n+1}-1=11\cdots11Bf(n)=∑i=0n2i=2n+1−1=11⋯11B (共 n+1n + 1n+1 个 111),计算 f(n)f(n)f(n) 的 C 语言程序如下:
int f1(unsigned n) {int sum = 1, power = 1;for (unsigned i = 0; i <= n - 1; i++) {power *= 2;sum += power;}}
将 f1 中的 int 都改为 float,可得到计算 f(n)f(n)f(n) 的 另一个函数 f2。假设 unsigned 和 int 型数据都占 323232 位,float 采用 IEEE 754 单精度标准。请回答下列问题:
α\alphaα. 当 n=0n = 0n=0 时,f1 会出现死循环,为什么❓️
n=0n = 0n=0 时,n - 1 的机器数为全 1, 对应的无符号数为 232−12^{32} - 1232−1,为 unsigned 型所能表示的最大数, i<=n−1i <= n-1i<=n−1 恒真,因此会出现死循环。
若将 f1 中的变量 iii 和变量 nnn 都定义为 int 型,则 f1 是否还会出现死循环❓️为什么❓️
不会出现死循环
n=0n = 0n=0 时,n - 1 的机器数为全 1, 对应的有符号数为 −1-1−1
当 i=0i = 0i=0 时,i<=n−1i <= n-1i<=n−1 不成立,跳出循环
β\betaβ. f1(23) 和 f2(23) 的返回值是否相等❓️机器数格式是什么(用十六进制表示)❓️
f1(23) 和 f2(23) 的返回值相等,均为 224−12^{24} - 1224−1
f1(23) 的机器数格式:
00000000111111111111111111111111=00FFFFFFH00000000\ 11111111\ 11111111\ 11111111 = 00FF\ FFFFH00000000 11111111 11111111 11111111=00FF FFFFH
f2(23) 的机器数格式:
1⋯1=1.1⋯1×2231\cdots1=1.1\cdots1\times2^{23}1⋯1=1.1⋯1×223
1.M=1.1⋯11.M = 1.1\cdots11.M=1.1⋯1 E=23+127=150=10010110E = 23 + 127 = 150 = 10010110E=23+127=150=10010110
01001011011111111111111111111111=4B7FFFFFH0\ 10010110\ 11111111111111111111111 = 4B7F\ FFFFH0 10010110 11111111111111111111111=4B7F FFFFH
γ\gammaγ. f1(24) 和 f2(24) 的返回值分别为 335544313355443133554431 和 33554432.033554432.033554432.0,为什么不相等❓️
当 n=24n = 24n=24 时,有效位数有 252525 位
float 只有 242424 位有效位,舍入后数值 +1+ 1+1
δ\deltaδ. f(31)=232−1f(31) = 2^{32} - 1f(31)=232−1,而 f1(31) 的返回值却为 −1-1−1 ,为什么❓️
f(31)f(31)f(31) 已经超出 int 的表示范围
机器数为全 111, 作为 int 时其值为 −1-1−1
若使 f1(n) 的返回值与 f(n)f(n)f(n) 相等时,最大的 nnn 是多少❓️
int 型最大值为 231−12^{31} - 1231−1,因此 nnn 最大为 303030
ϵ\epsilonϵ. f2(127) 的机器数为 7F800000H7F80\ 0000H7F80 0000H,对应的值是什么❓️
011111111000000000000000000000000\ 11111111\ 000000000000000000000000 11111111 00000000000000000000000
IEEE 754 用阶码全 111,尾数全 000 表示 ∞\infty∞
因此 f2(127)=+∞f2(127) = +\inftyf2(127)=+∞
若使 f2(n) 的结果不溢出,最大的 nnn 是多少❓️
IEEE 754 最大阶码 11111110=25411111110 = 25411111110=254 e=254−127=127e = 254 - 127 = 127e=254−127=127
减去尾数舍入的 111, e=126e = 126e=126
1.1⋯1×2126=2127−1=f(126)1.1\cdots1\times2^{126} = 2^{127} - 1 = f(126)1.1⋯1×2126=2127−1=f(126)
若使 f2(n) 的结果不溢出,最大的 nnn 是 126126126
若使 f2(n) 的结果精确(无舍入),最大的 nnn 是多少❓️
IEEE 754 尾数 242424 位有效位, f(23)f(23)f(23) 为 242424 个 111,无需舍入
若使 f2(n) 的结果精确(无舍入),最大的 nnn 是 232323
算术逻辑单元 ALU
串行加法器和并行加法器
① 全加器
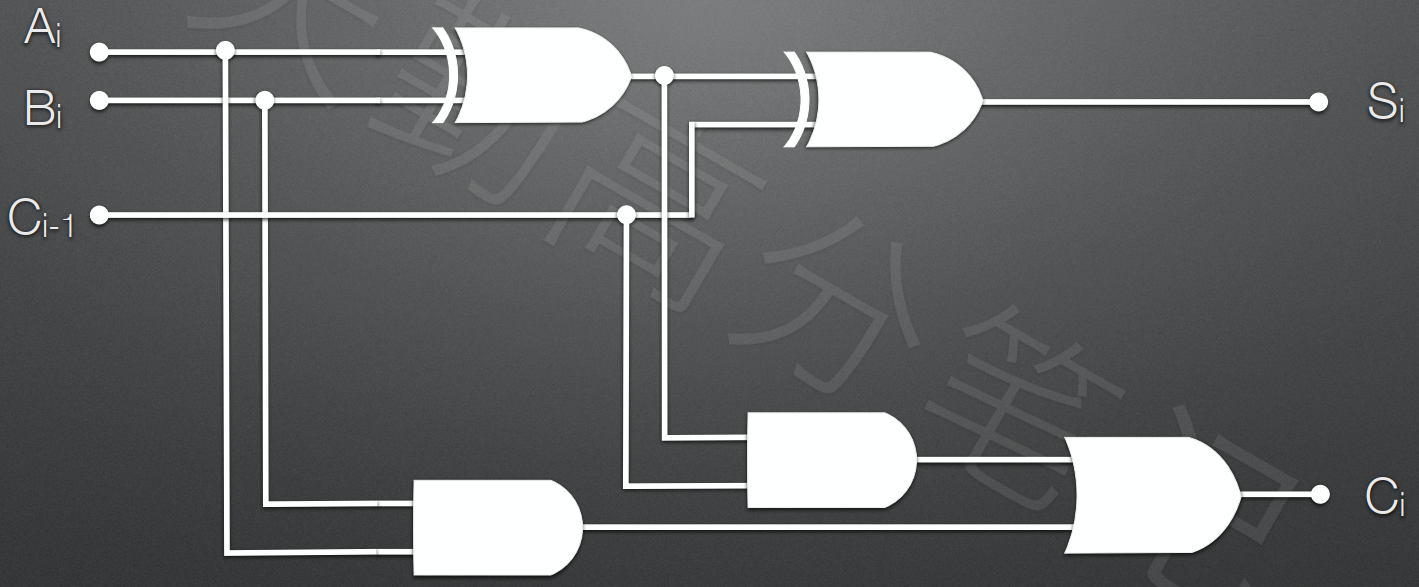
求和单元:Si=Ai⊕Bi⊕Ci−1S_i = A_i \oplus B_i \oplus C_{i-1}Si=Ai⊕Bi⊕Ci−1
进位链:Ci=AiBi+(Ai⊕Bi)Ci−1C_i = A_iB_i + (A_i \oplus B_i)C_{i-1}Ci=AiBi+(Ai⊕Bi)Ci−1
② 串行加法器
只设一个全加器的加法器称为串行加法器。两个操作数分别放在两个移位寄存器中,并且由移位寄存器从低位到高位串行地提供操作数进行相加。如果操作数长 16 位,就要分成 16 步进行,每步产生 1 位和,串行地送入结果寄存器,而产生的进位信号只需要 1 位触发器,每完成 1 步,用新的进位覆盖旧的进位。
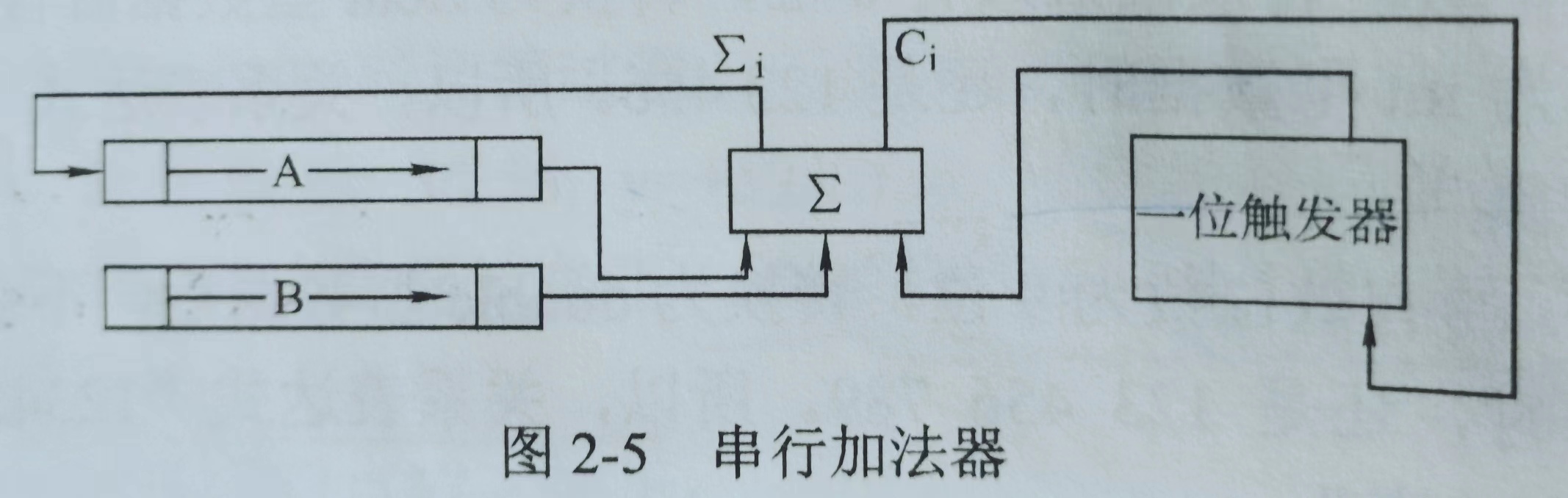
③ 并行加法器(串行进位链)
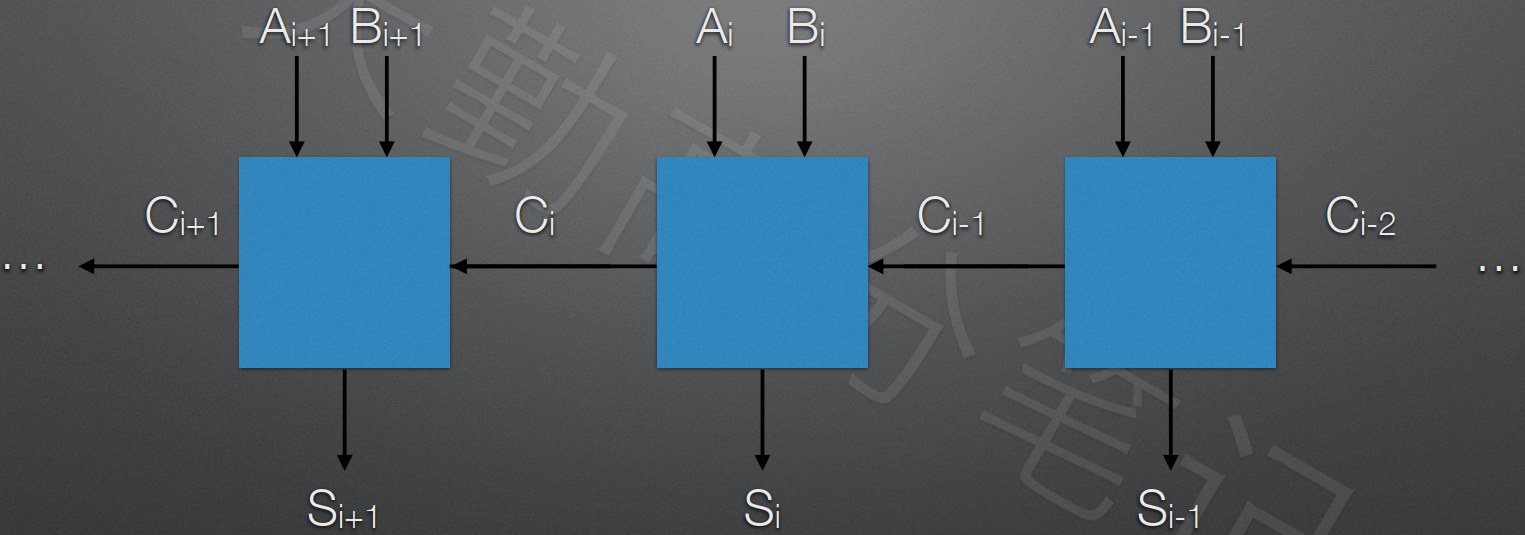
解决了求和的一些延迟问题,但是低位向高位产生的进位来得太晚了。
④ 并行加法器(并行进位链) ⭐️
进位条件:Pi=Ai⊕BiP_i = A_i \oplus B_iPi=Ai⊕Bi
本地进位:Gi=AiBiG_i = A_iB_iGi=AiBi
C1=G1+P1C0C_1 = G_1 + P_1C_0C1=G1+P1C0
C2=G2+P2C1=G2+P2(G1+P1C0)C_2 = G_2 + P_2C_1 = G_2 + P_2(G_1 + P_1C_0)C2=G2+P2C1=G2+P2(G1+P1C0)
C3=G3+P3C2=G3+P3(G2+P2(G1+P1C0))C_3 = G_3 + P_3C_2 = G_3 + P_3(G_2 + P_2(G_1 + P_1C_0))C3=G3+P3C2=G3+P3(G2+P2(G1+P1C0))
C4=G4+P4C3=G4+P4(G3+P3(G2+P2(G1+P1C0)))C_4 = G_4 + P_4C_3 = G_4 + P_4(G_3 + P_3(G_2 + P_2(G_1 + P_1C_0)))C4=G4+P4C3=G4+P4(G3+P3(G2+P2(G1+P1C0)))
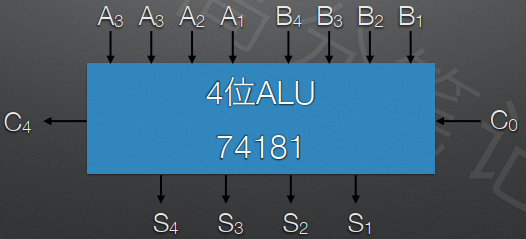
⑤ 组内并行组间串行方式(单级先行进位方式) ⭐️
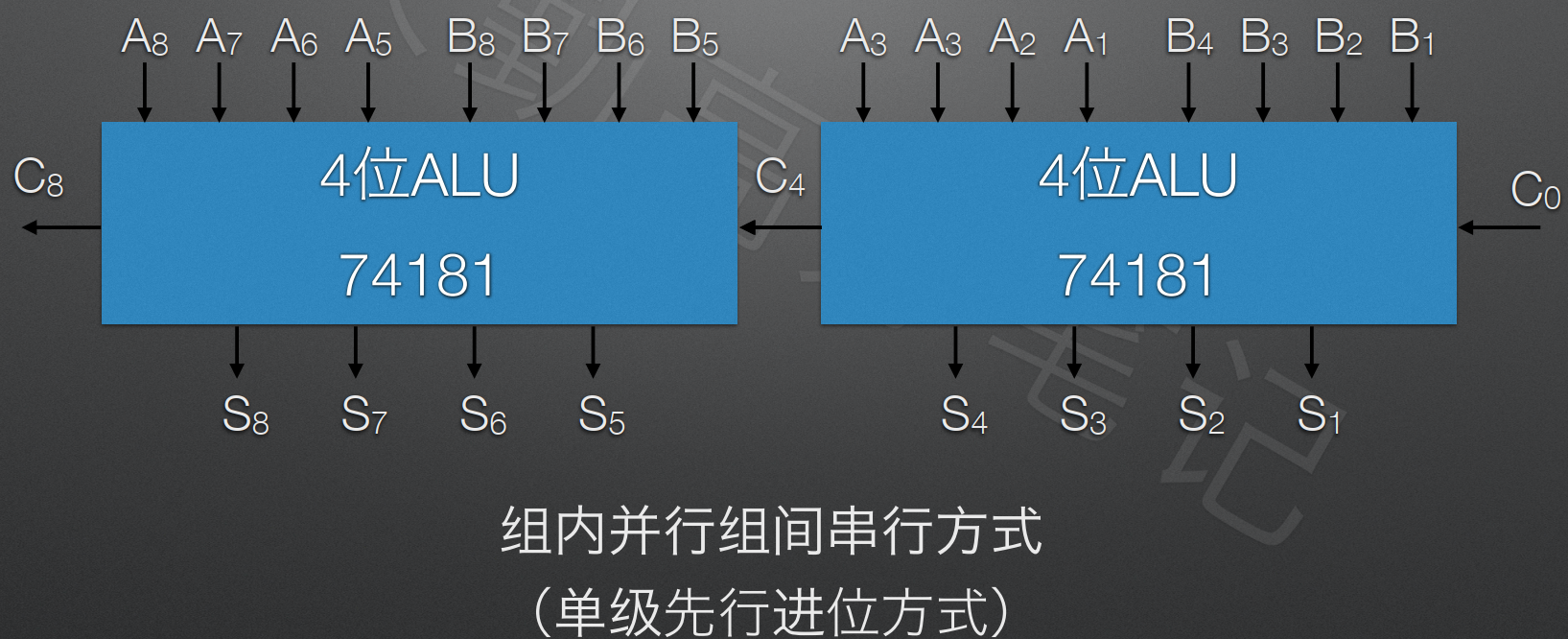
注意 🔔 :
加法器采用先行进位 的根本目的是 快速传递进位信号
⑥ 组内并行组间并行方式(多级先行进位方式) ⭐️⭐️

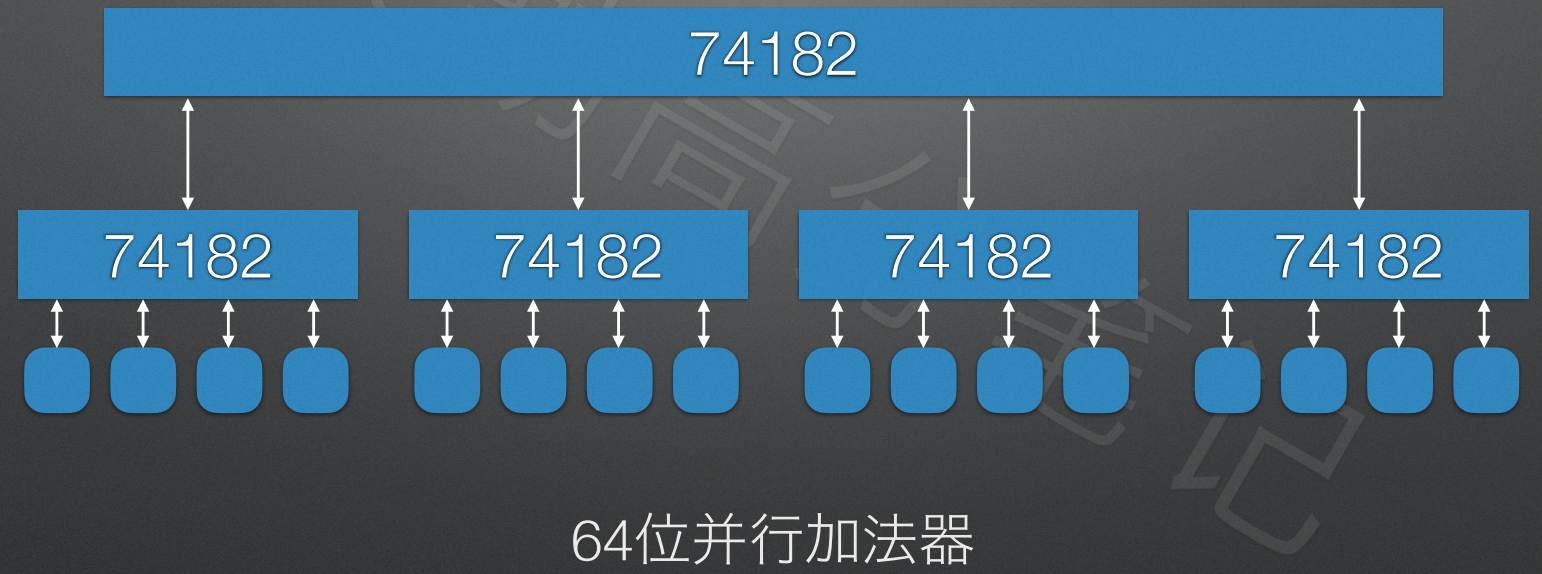
算术逻辑单元的功能和结构
① 数字电路
组合逻辑电路:任意时刻的 输出 仅仅取决于该时刻的输入,与电路原来的状态无关。也就是说,组合逻辑电路 没有“记忆”,运算后的结果要 立刻送入寄存器保存。
时序逻辑电路:任意时刻的 输出 不仅取决于当时的输入信号,还 取决于电路原来的状态。也就是说,时序逻辑电路 具有记忆元件,即 触发器(能够存储 1 位 信号的基本单元电路),可以记录前一时刻的输出状态(CPU 就是一种复杂的 时序逻辑电路)。
ALU 是一种 组合逻辑电路,因此在实际使用 ALU 时,其 输入端口 A 和 B 必须和锁存器(多位触发器)相连,而且在运算的过程中 锁存器的内容是不变的,其输出也必须送至寄存器保存。
② ALU 的主要功能:算术运算、逻辑运算、先行进位
③ ALU 的结构:
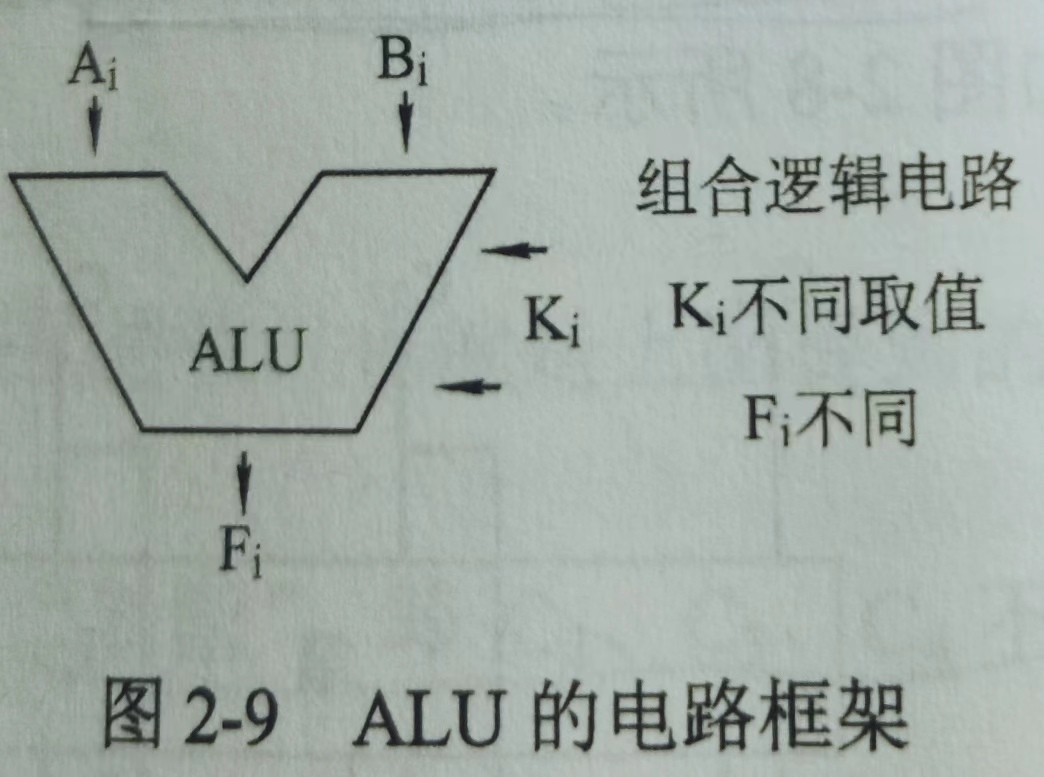
Ai,BiA_i, B_iAi,Bi 为输入变量;KiK_iKi 为控制信号,KiK_iKi 的不同取值可以决定该电路进行哪一种算术运算和哪一种逻辑运算;FiF_iFi 为输出函数。
相关文章:

计算机组成原理 - 2. 数据的表示和运算
整理自天勤高分笔记,购书链接: 24 天勤高分笔记 要记住的几个数字 📓: 215327682^{15} 3276821532768 216655362^{16} 6553621665536 23121474836482^{31} 21474836482312147483648 23242949672962^{32} 4294967296232429496…...

【js】基础知识点--语句,break和continue,switch,with,for..in,do-while,while
一、break和continue语句,常用 break 语句会立即退出循环,强制继续执行循环后面的语句。而 continue 语句虽然也是立即退出循环,但退出循环后会从循环的顶部继续执行 var num 0; for (var i1; i < 10; i) {if (i % 5 0) {break;}num; …...
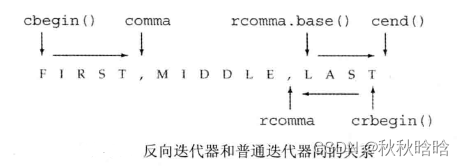
【C++】迭代器
内容来自《C Primer(第5版)》9.2.1 迭代器、9.2.3 begin和end成员、9.3.6 容器操作可能使迭代器失效、10.4.3 反向迭代器 目录 1. 迭代器 1.1 迭代器范围 1.2 使用左闭合范围蕴含的编程假定 2. begin和end成员 3. 容器操作可能使迭代器失效 3.1 编…...

数据可视化在前端中的应用
前端开发中,数据可视化是一种非常重要的技术。它可以将复杂的数据以图形化的方式展示出来,让用户更容易理解和分析数据。在前端中,VUE是一种非常流行的JavaScript框架,可以用来实现各种数据可视化效果。 首先,让我们来看看一些常见的数据可视化方式: 表格:表格是数据可…...

FFmpeg 合并视频文件没声音,不同步原因
查了不少帖子也没搞明白,可能懂的人不会遇到吧。 1 没声音是因为我几个视频文件中,有的没音轨,就是用文字生成了个视频,需要先给它加个dummy的音轨才行。 2 视频不同步是因为各个视频格式不一样,参数挺多我也不知道具…...

绕不开的“定位”
绕开“定位”这个词谈企业战略和品牌 相当于揪住头发离开地球 定位这个词,已经进入商业界的心智中去了 发明这个词的特劳特和里斯的思想有啥差异? 《定位屋》刨析的很到位 趣讲大白话:把握概念的源头,就理解对了大部分 【趣讲信息…...
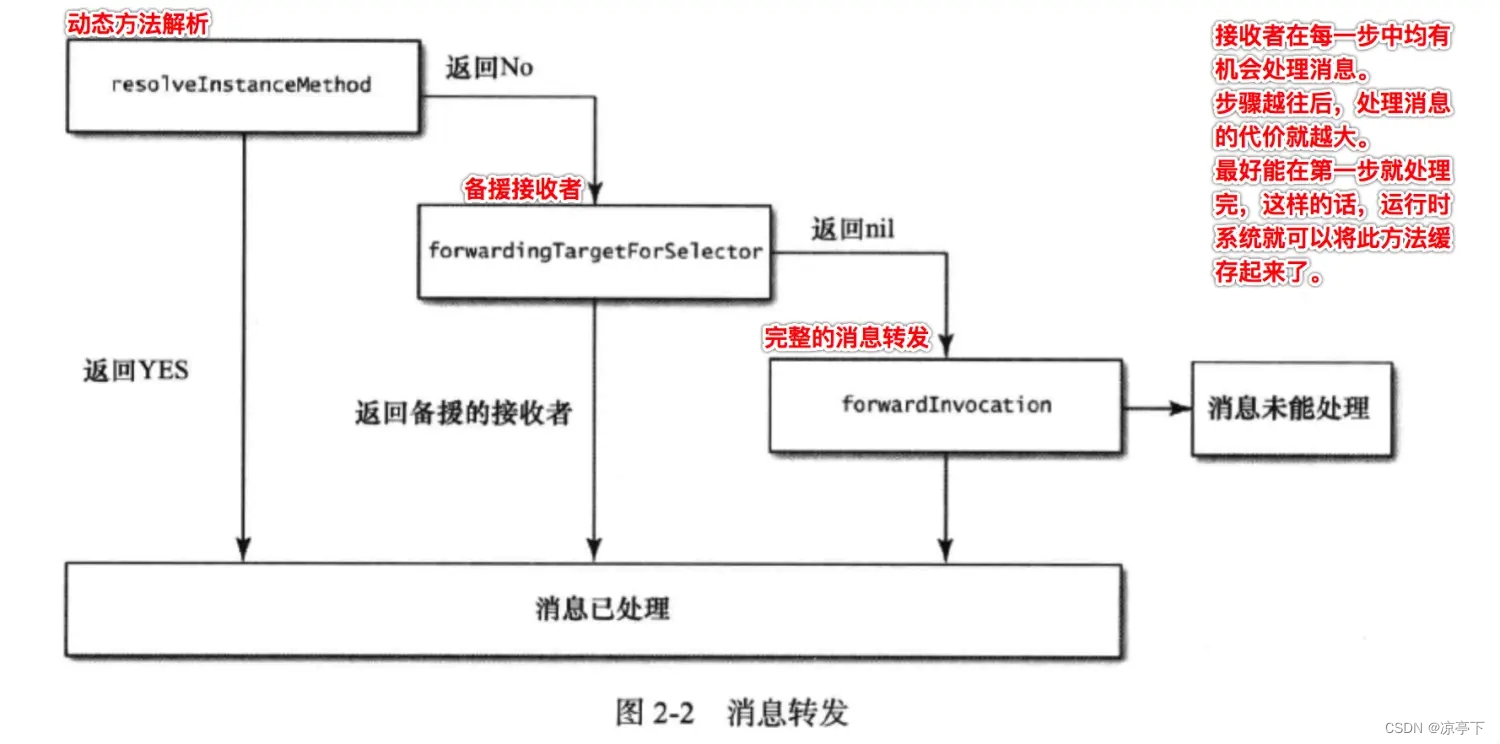
《Effective Objective-C 2.0 》 阅读笔记 item12
第12条:理解消息转发机制 1. 消息转发机制 当对象接收到无法解读的消息后,就会启动“消息转发”机制,开发者可经由此过程告诉对象应该如何处理未知消息。 消息转发分为两大阶段 第一阶段:先征询接收者所属的类,看其…...

云原生计算能消除技术债务吗?
云原生计算可以将行业领域驱动的设计、GitOps和其他现代软件最佳实践汇总起来,如果企业实施得当,可以减少技术债务。 云原生计算是企业IT的一种新范式,它涉及现代技术的方方面面,从应用程序开发到软件架构,再到保持一…...

9. 回文数
题目 给你一个整数 xxx ,如果 xxx 是一个回文整数,返回 truetruetrue ;否则,返回 falsefalsefalse 。回文数是指正序(从左向右)和倒序(从右向左)读都是一样的整数。 例子 输入&am…...

[SV]SystemVerilog线程之fork...join专题
SystemVerilog线程之fork...join专题 Q:fork-join_none开辟的线程在外部任务退出后也会结束吗? A:后台线程不会结束,任何由fork开辟的线程(join、join_any、join_none),无论其外部任务ÿ…...
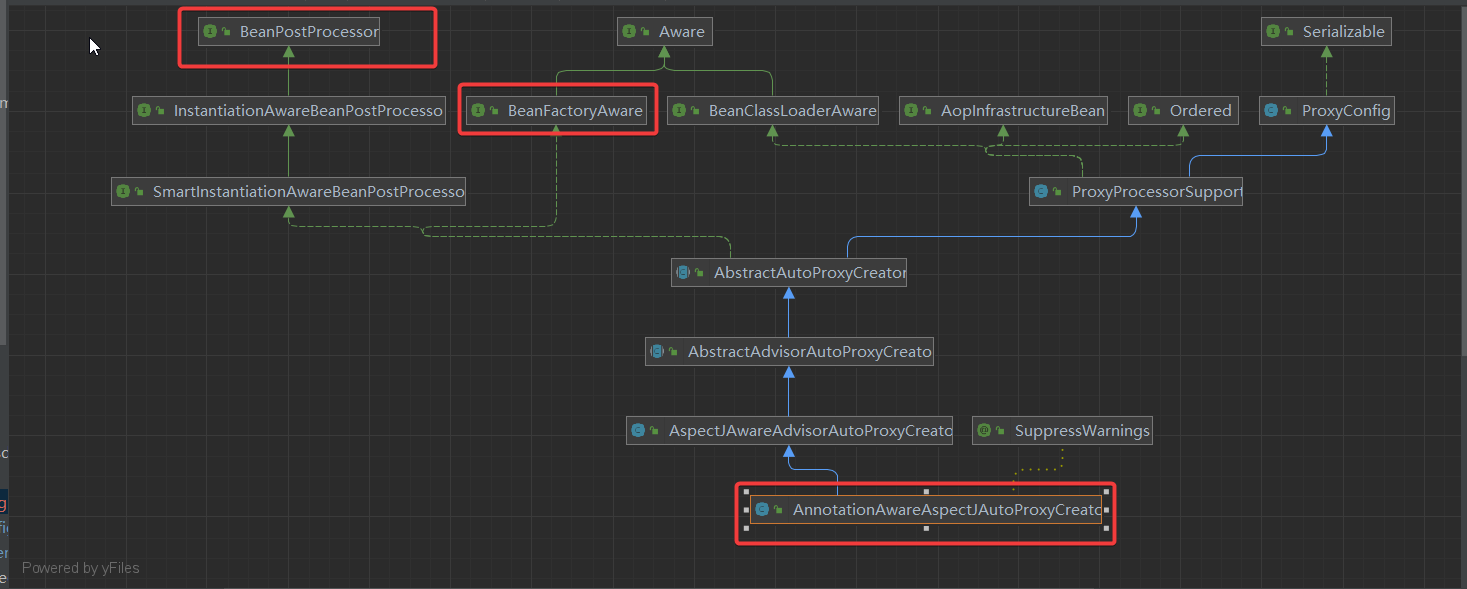
你看这个spring的aop它又大又宽
aop🚓AOP 分类AspectJ | 高级但是难用Spring AOP | 易用但仅支持方法aop 原理明月几时有,把酒问青天。——唐代李白《将进酒》 AOP 分类 在 Spring Boot 中,AOP 的实现主要有以下几种: 基于 AspectJ 的 AOP:这是一种基…...

设计模式-创建-单例模式
4.1.1 模式介绍 定义 单例模式(Singleton Pattern)是 Java 中最简单的设计模式之一,此模式保证某个类在运行期间,只有一个实例对外提供服务,而这个类被称为单例类。 作用 保证一个类只有一个实例为该实例提供一个全…...
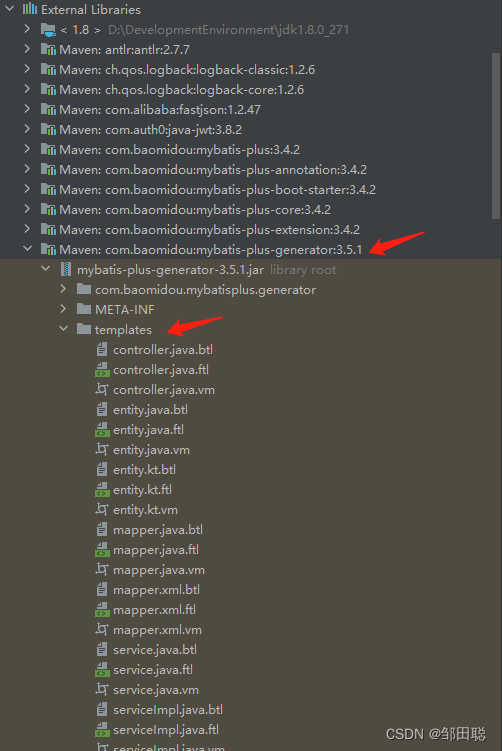
使用mybatis-plus-generator配置一套适合你的CRUD
1、maven引入 mybatis-plus-generator 和模板引擎,你也可以使用freemarker之类的,看个人 <!-- mybatisplus代码生成器 --><dependency><groupId>com.baomidou</groupId><artifactId>mybatis-plus-generator</artifactI…...
)
MATLAB实现各种离散概率密度函数(概率密度/分布/逆概率分布函数)
MATLAB实现各种离散概率密度函数(概率密度/分布/逆概率分布函数) 1 常见离散概率分布的基本信息2 常见离散概率分布计算及MATLAB实现2.1 二项分布(Binomial Distribution)2.1.1 常用函数2.2 负二项分布(Negative Binomial Distribution)2.2.1 常用函数2.3 几何分布(Geom…...

指针的基本知识
我们不会用bit去表达一个数据,因为只能放0和1,能表达的数据太少了,内存地址最小单位是字节 11111111 0x0011 1字节8bit,8bit才算作一个地址,地址是以字节为最小单位&#…...
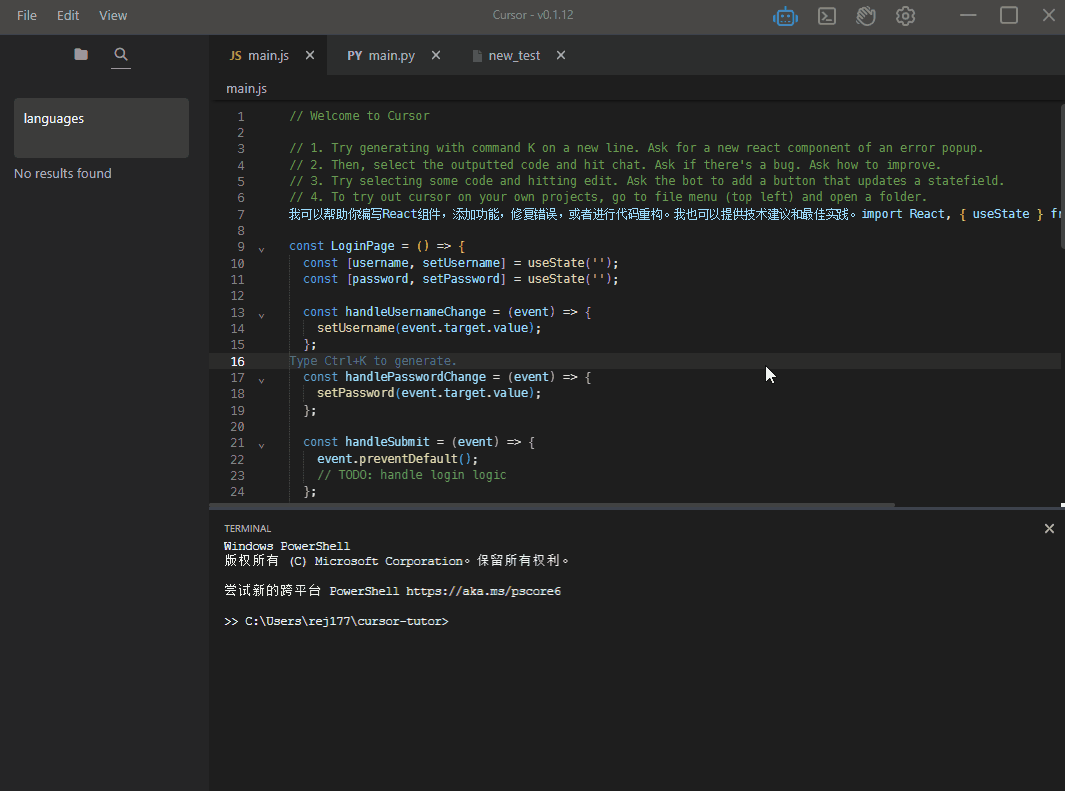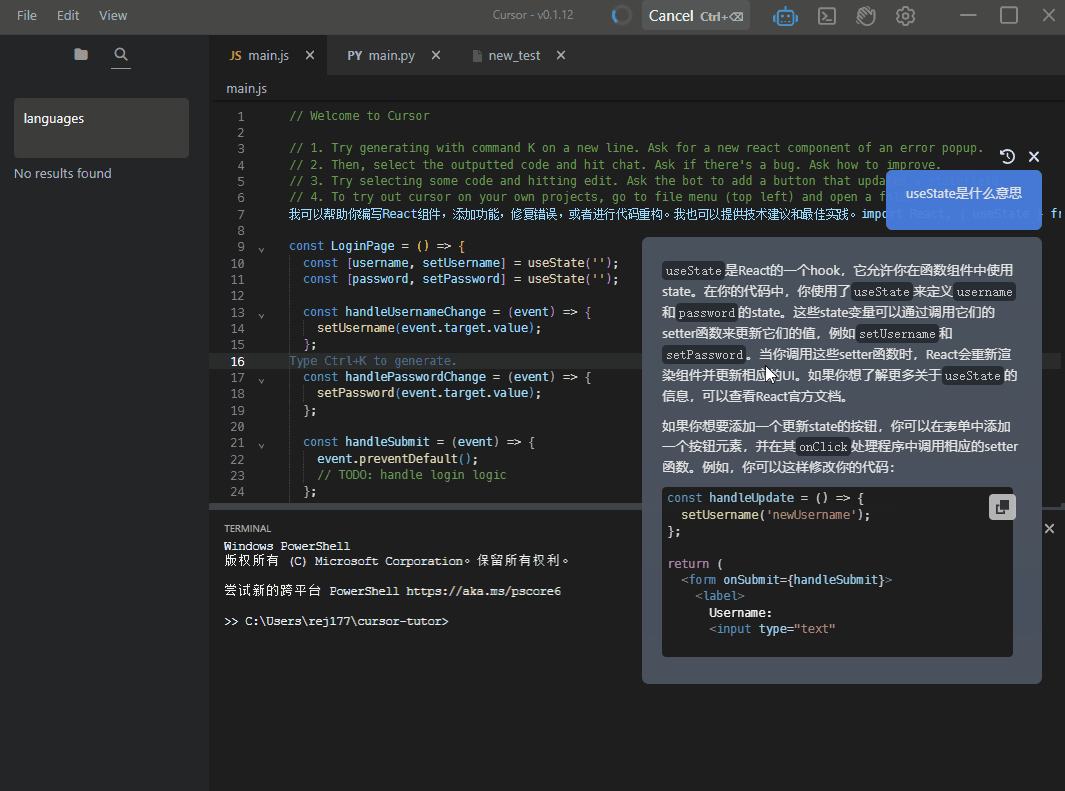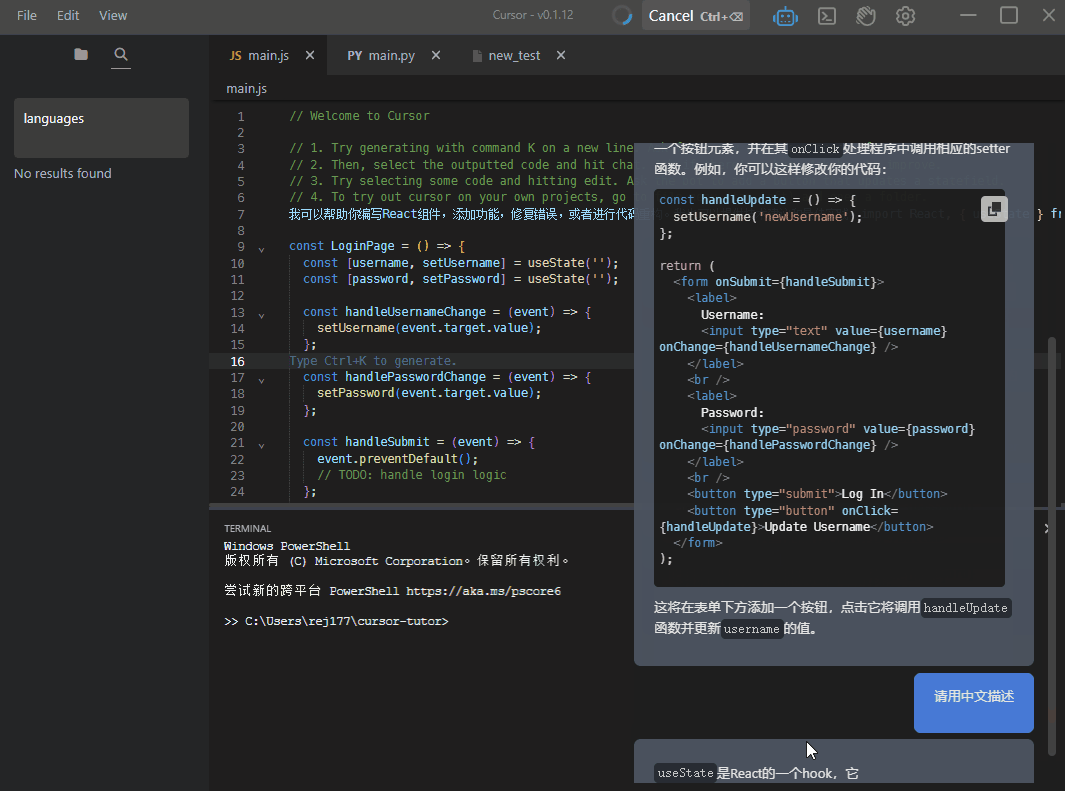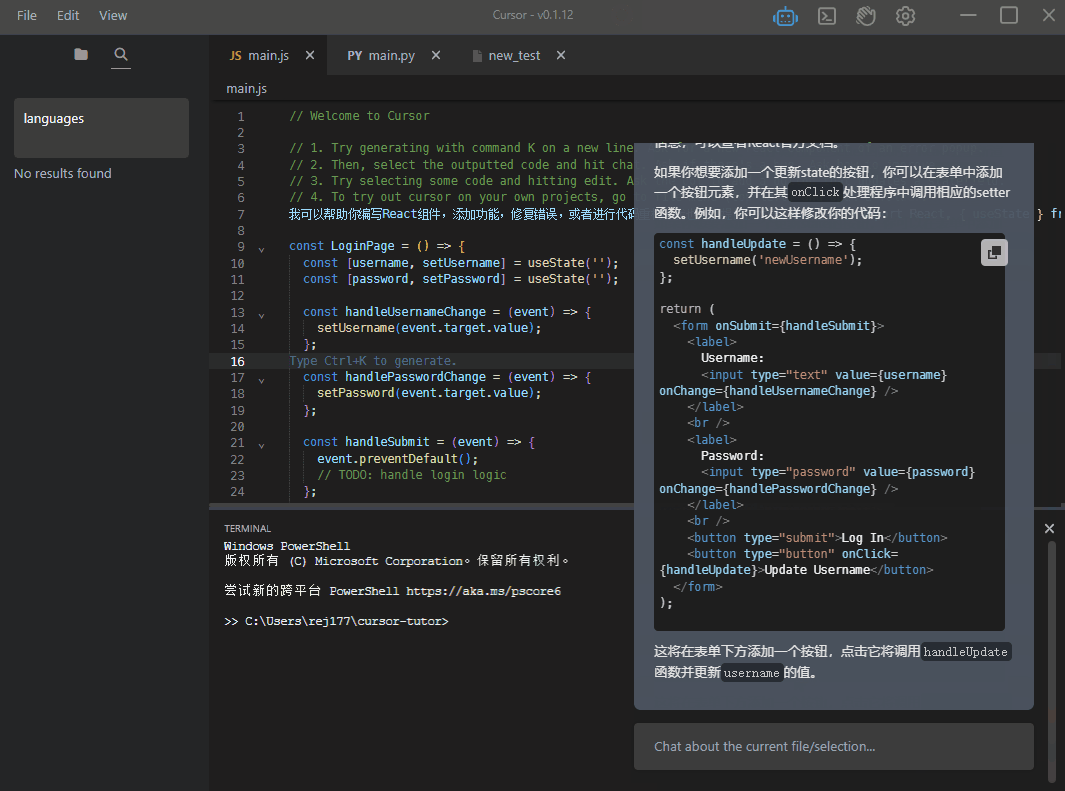
当你的IDE装上GPT
文章目录前言下载安装使用步骤前言 我们可能要从“CV”工程师变成“KL工程师了,为什么叫”KL“工程师呢, 因为只要K和L两个指令就可以直接生成代码、修改代码,哪行代码不会点哪里,他都给你解释得明明白白。 提示:以下…...

一图看懂 pathlib 模块:面向对象的文件系统路径, 资料整理+笔记(大全)
本文由 大侠(AhcaoZhu)原创,转载请声明。 链接: https://blog.csdn.net/Ahcao2008 一图看懂 pathlib 模块:面向对象的文件系统路径, 资料整理笔记(大全)摘要模块图类关系图模块全展开【pathlib】统计常量intbooltuple模块9 fnmatc…...
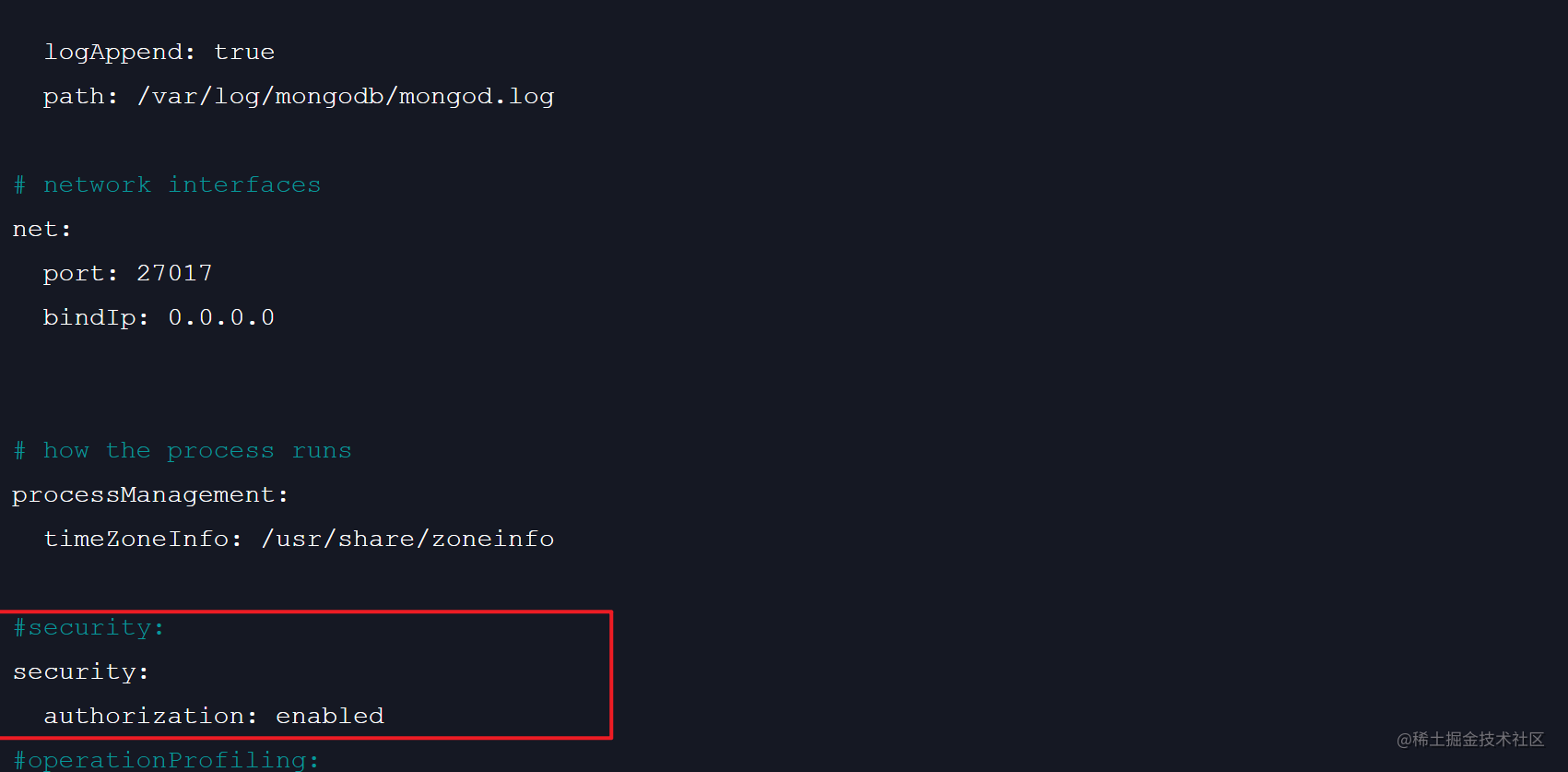
前端如何将node.js 和mongodb部署到linux服务器上
本文首发自掘金。 记录了我第一次成功部署node.js 和mongodb到linux服务器上了,期间也遇到一些小坑,但是网上各位大佬记录的文章帮了大忙,所以我也将过程记录了下来。 安装Node 使用nvm linux上安装node,肯定首选nvmÿ…...

mysql数据迁移
背景:随着时间的推移,交易系统中的订单表越来越大,目前达到500w数据。为了防止数据量过大导致的查询性能问题,现将订单表进行拆分,分为实时库和历史库。实时库保留近6个月的数据,用于退款业务需求ÿ…...

【4.3蓝桥备战】小朋友崇拜圈、正则问题
文章目录小朋友崇拜圈正则问题小朋友崇拜圈 小朋友崇拜圈 - 蓝桥云课 (lanqiao.cn) 拿到这道题要先把题目读懂。 下面的一行是表示:编号为i的小朋友,崇拜的对象为编号为path[i]的小朋友。 本题应该使用DFS,深度优先遍历找到可以成环的崇拜圈…...

Chapter03-Authentication vulnerabilities
文章目录 1. 身份验证简介1.1 What is authentication1.2 difference between authentication and authorization1.3 身份验证机制失效的原因1.4 身份验证机制失效的影响 2. 基于登录功能的漏洞2.1 密码爆破2.2 用户名枚举2.3 有缺陷的暴力破解防护2.3.1 如果用户登录尝试失败次…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

微服务通信安全:深入解析mTLS的原理与实践
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、引言:微服务时代的通信安全挑战 随着云原生和微服务架构的普及,服务间的通信安全成为系统设计的核心议题。传统的单体架构中&…...

论文阅读:Matting by Generation
今天介绍一篇关于 matting 抠图的文章,抠图也算是计算机视觉里面非常经典的一个任务了。从早期的经典算法到如今的深度学习算法,已经有很多的工作和这个任务相关。这两年 diffusion 模型很火,大家又开始用 diffusion 模型做各种 CV 任务了&am…...
