【电路】1.1 实际电路和电路模型
1.1 实际电路和电路模型
科学理论的研究对象是现实世界背后的抽象世界,如:
- 数学中的 ∞ \infty ∞,
- 经典力学中“质点”的概念,
- 牛顿运动定律(如惯性定律,如果一个物体不受外力情况下,一直保持匀速或者静止状态,但是现实世界绝对不会出现这种情况)等
电路理论所研究的对象也是抽象的,我们用抽象世界的研究成果去改造现实世界。
比如一个现实中的电感线圈通入电流后,会发热(能量损耗),电流通过线圈会激发磁场,它会在任意两匝金属圈之间会形成电容(电场)

- 现实生活中的电感线圈:能量损耗,磁场储能,电场储能。
- 理想电感:只反映磁场储能,现实生活中不存在,是人脑抽象所得产物。
1.1.1 实际电路器件
实际电路器件同时伴随电场、磁场、能量损耗三种物理过程,很复杂。
1.1.2 理想电路元件
理想电路元件只反映一种物理过程
-
电阻:只反映能量损耗,通过电流后,不会有任何电场和磁场,只有能量损耗。

-
电感:只反映磁场储能,通过电流以后,不会有电场和能量损耗。

-
电容:只反映电场储能,加了电压以后不会有磁场和能量损耗。

通过这种思路,我们就导出了理想电路元件RLC。
结合实际电路的工作情况,用理想电路元件的组合恰当地反映其主要电磁过程,此过程称之为建模。比如,如果有一个现实的电感,如果它发热,就在理想电感的基础上串联一个理想的电阻就行,如果工作频率高一些,那就再并联一个理想的电容,如果这个电感线圈导电性非常好,就不用串联一个理想的电阻。
1.1.3 实际电路
实际电路由实际元器件构成,它呈现出复杂的电磁性质:同时伴随着电场效应、磁场效应、能量损耗。它是为完成某些具体功能而精心设计出的现实生活中的电路,如计算器、体重秤、电脑、电力系统等。
1.1.4 理想化电路模型
理想化电路模型由理想原件构成,是人类对实际电路进行抽象所得到的一种理想化科学模型。
-
电阻只反映能量损耗;

-
电感只反映磁场储能;

-
电容只反映电场储能;

-
理想导线无任何电磁性质(比如不产生(螺旋定则)产生磁场),它唯一的作用就是形成电流的通路。

1.1.5 电动机的电路模型
- 工作原理:电磁感应定律,工作时内部需建立磁场,电感 L L L反映磁场储能特性
- 拖动负载转动,即作工(电能消耗),电阻 R R R反映能量损耗性质。

1.1.6 按照端子数区分电路元件
对外引出线(即接头)称之为端子,也叫端钮。
- 二端元件:有两个引出接头

- 三端元件:

- 四端元件:

1.1.6 补充知识点
- 后面分析的对象都是理想化电路元件构成的理想化电路模型。
- 电路分析的基本目的是计算电路中各支路的电压电流。
- 一个完整的电路通常是包含电源、中间环节、负载。
- 电源可称之为激励、任意支路电压、电流称之为响应。
- 电源可称之为输入,任意支路电压、电流称之为输出。
- 整个电路是一个封闭系统,内部满足能量平衡、遵循能量守恒定律。
- 瞬时值等随时间变化的量,我们通常用小写字母表示;而恒定的、不随时间变化的量,我们通常用大写字母表示。
- 电路中所涉及的物理量:电压( u u u),电流( i i i),电荷( q q q),磁链( ψ \psi ψ)、功( p p p)、电能( w w w)等
相关文章:

【电路】1.1 实际电路和电路模型
1.1 实际电路和电路模型 科学理论的研究对象是现实世界背后的抽象世界,如: 数学中的 ∞ \infty ∞,经典力学中“质点”的概念,牛顿运动定律(如惯性定律,如果一个物体不受外力情况下,一直保持匀…...

Vue - 打包部署
vscode找到NPM脚本,点击build。 目录下出现dist目录则表示安装成功。 安装Nginxnginx: download 目录用途conf配置文件目录html静态资源文件目录logs日志文件目录temp临时文件目录 将刚刚打包好的文件放到html目录下。 点击nginx.exe,用localhost:默认…...

spring揭秘25-springmvc03-其他组件(文件上传+拦截器+处理器适配器+异常统一处理)
文章目录 【README】【1】文件上传与MultipartResolver【1.1】使用MultipartResolver进行文件上传【1.2】springmvc处理multipart多部件请求流程【1.3】使用springmvc上传文件代码实现(springmvc6.10版本): 【2】Handler与HandlerAdaptor&…...

springboot项目中属性的使用优先级;maven编译插件切换环境变量
概述 在项目部署时,相关的生产环境和测试环境是分开的,但是代码是同一套; 所以一般会有多套变量; 项目中默认变量(一般是测试环境) 线上变量(线上数据较敏感,一般也不会放在代码中&…...
【Qt】控件概述 (1)—— Widget属性
控件概述 1. QWidget核心属性1.1核心属性概述1.2 enable1.3 geometry——窗口坐标1.4 window frame的影响1.4 windowTitle——窗口标题1.5 windowIcon——窗口图标1.6 windowOpacity——透明度设置1.7 cursor——光标设置1.8 font——字体设置1.9 toolTip——鼠标悬停提示设置1…...
(笔记)第三期书生·浦语大模型实战营(十一卷王场)–书生基础岛第3关---浦语提示词工程实践
学员闯关手册:https://aicarrier.feishu.cn/wiki/ZcgkwqteZi9s4ZkYr0Gcayg1n1g?open_in_browsertrue 课程视频:https://www.bilibili.com/video/BV1cU411S7iV/ 课程文档: https://github.com/InternLM/Tutorial/tree/camp3/docs/L1/Prompt 关…...
视频采集类VideoCapture之设置视频捕获设备的属性函数 set()的使用)
OpenCV视频I/O(11)视频采集类VideoCapture之设置视频捕获设备的属性函数 set()的使用
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 VideoCapture 中设置一个属性。 在OpenCV中,cv::VideoCapture::set() 函数用于设置视频捕获设备的属性。这些属性可以包括分辨率、…...

数据结构之树(3)
一、森林和树的转换 重要! 树->二叉树 由于孩子兄弟链式存储和二叉树链式存储本质相同,故树可转换为二叉树。 森林->二叉树 森林:m棵互不相交的树的集合 森林->树 树->二叉树 森林中各个树的根节点之间视为兄弟关系 二、树…...

螺蛳壳里做道场:老破机搭建的私人数据中心---Centos下docker学习02(yum源切换及docker安装配置)
2 前期工作 2.1 切换yum源并更新 删除/etc/yum.repos.d/原有repo文件,将Centos-7.repo库文件拷贝到该目录下。 然后清楚原有缓存yum clean all 生成新的缓存yum makecache 更新yum update –y 然后再确认/etc/yum.repos.d/不会有其他库文件,只留下…...

强化学习笔记之【Q-learning算法和DQN算法】
强化学习笔记(一)——Q-learning和DQN算法核心公式 文章目录 强化学习笔记(一)——Q-learning和DQN算法核心公式前言:Q-learning算法DQN算法 前言: 强化学习领域,繁冗复杂的大段代码里面&#…...

面试经验02
嵌入式简历制作指南与秋招求职建议 引言 秋招季即将到来,许多同学开始准备求职简历。无论你是考研失利准备就业,还是即将毕业寻找实习,一份优秀的简历都是求职的敲门砖。今天,我们将讨论如何制作嵌入式领域的求职简历࿰…...

分层图 的尝试学习 1.0
分层图: 分层图的最短路: 又叫做 扩点最短路。不把实际位置看做是图上的点,而是把实际位置及其状态的组合,(一个点有若干的状态,所以一个点会扩充出来若干点)看做是图上的点,然后搜索…...

第 31 章 javascript 之 XPath
第 31 章 XPath 1.IE 中的 XPath 2.W3C 中的 XPath 3.XPath 跨浏览器兼容 XPath 是一种节点查找手段,对比之前使用标准 DOM 去查找 XML 中的节点方式,大大降低了查找难度,方便开发者使用。但是,DOM3 级以前的标准并没有就 XPa…...

JavaScript中的高阶函数
高阶函数 所谓高阶函数,就是操作函数的函数,它接收一个或多个函数作为参数,并返回一个新函数: 来看一个mapper()函数,将一个数组映射到另一个使用这个函数的数组上: 更常见的例子,它接收两个函…...
Qt6.7开发安卓程序间接连接到MySQL的方法
本文主要描述一种通过间接的方法,使得Qt开发的安卓程序可以直连到Mysql数据库的方法。本文章的方案是通过JAVA代码去连接MySQL数据库,然后C代码去调用JAVA的方法,从而实现QT开发的安卓程序去直连到MySQL数据库。 本文使用 JDBC 结合 JNI&…...

ROW_NUMBER
How to rewrite a query which uses the ROW_NUMBER() window function in versions 5.7 or earlier before window functions were supported e.g., SELECT ROW_NUMBER() OVER (PARTITION BY fieldA) AS rownum, myTable.* FROM myTable; index 用不上的 Solution Assuming…...

Docker技术
目录 Docker的基本概念 Docker的核心原理 Docker的使用场景 Docker的优点 Docker的挑战 为什么使用 环境一致性 快速启动和部署 资源利用率高 支持微服务架构 持续集成与持续交付(CI/CD) 依赖管理 简化部署流程 高效资源管理 生态系统丰富…...

中小企业做网站需要考虑哪些因素?
中小企业在建设网站时,需要考虑的因素有很多。以下是一些主要考虑因素的介绍: 明确建站目的:中小企业需要明确自己建立网站的目的。是为了展示企业形象、推广产品,还是提供客户服务?不同的目的将决定网站的设计和功能…...
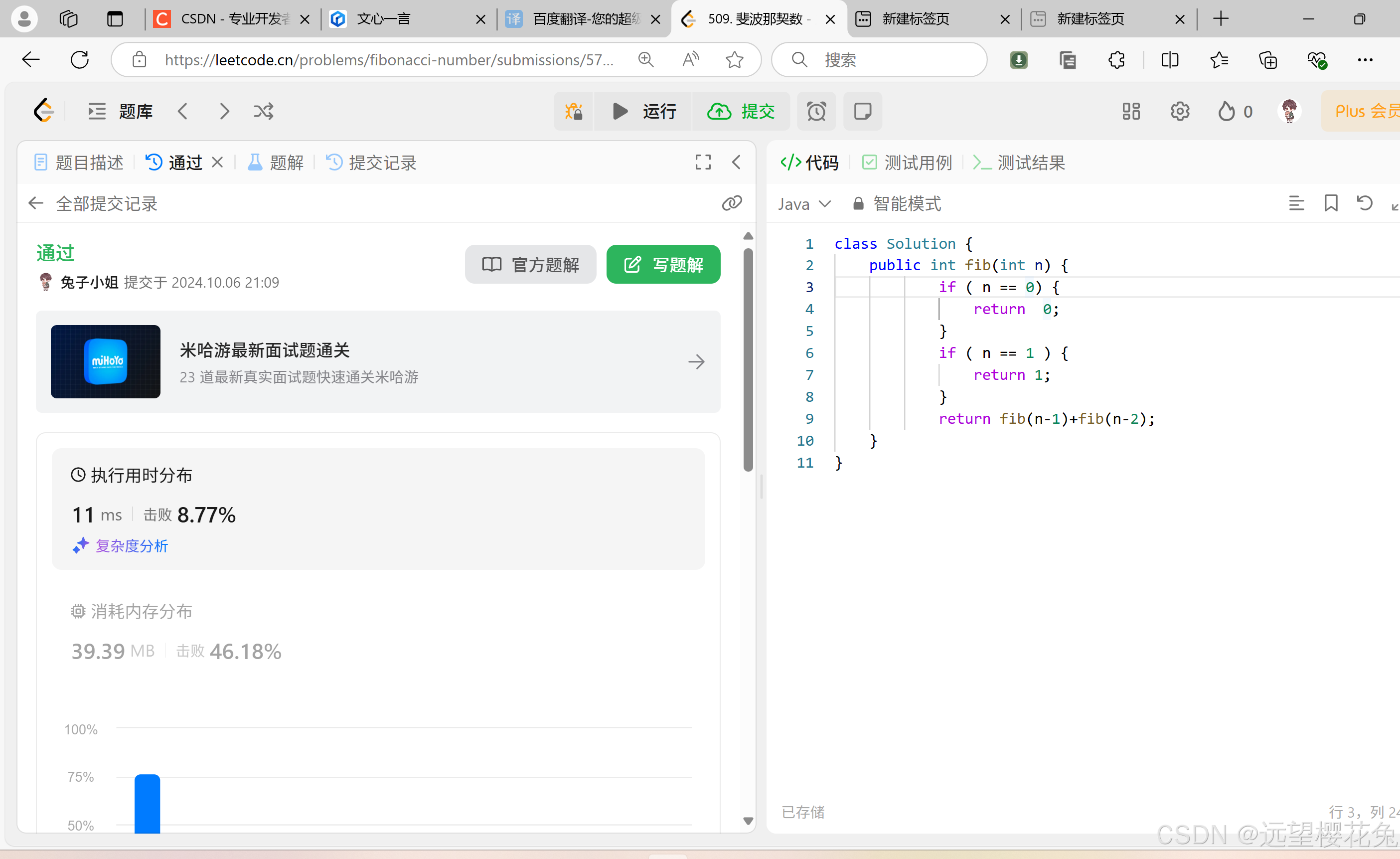
【d60】【Java】【力扣】509. 斐波那契数
思路 要做的问题:求F(n), F(n)就等于F(n-1)F(n-2),要把这个F(n-1)F(n-2)当作常量,已经得到的值, 结束条件:如果是第1 第2 个数字的时候,没有n-1和n-2,所以…...

项目-坦克大战学习-游戏结束
当boos受到伤害时游戏结束,游戏结束时我们需要将窗体全部绘制从别的画面,这样我们可以在游戏运行类中的update设置条件,在游戏运行类thread创建一个枚举类型定义是否游戏结束 public enum Game { play, over };//定义现在游戏运行状态 如果…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

保姆级教程:在无网络无显卡的Windows电脑的vscode本地部署deepseek
文章目录 1 前言2 部署流程2.1 准备工作2.2 Ollama2.2.1 使用有网络的电脑下载Ollama2.2.2 安装Ollama(有网络的电脑)2.2.3 安装Ollama(无网络的电脑)2.2.4 安装验证2.2.5 修改大模型安装位置2.2.6 下载Deepseek模型 2.3 将deepse…...

java高级——高阶函数、如何定义一个函数式接口类似stream流的filter
java高级——高阶函数、stream流 前情提要文章介绍一、函数伊始1.1 合格的函数1.2 有形的函数2. 函数对象2.1 函数对象——行为参数化2.2 函数对象——延迟执行 二、 函数编程语法1. 函数对象表现形式1.1 Lambda表达式1.2 方法引用(Math::max) 2 函数接口…...
之(六) ——通用对象池总结(核心))
怎么开发一个网络协议模块(C语言框架)之(六) ——通用对象池总结(核心)
+---------------------------+ | operEntryTbl[] | ← 操作对象池 (对象数组) +---------------------------+ | 0 | 1 | 2 | ... | N-1 | +---------------------------+↓ 初始化时全部加入 +------------------------+ +-------------------------+ | …...
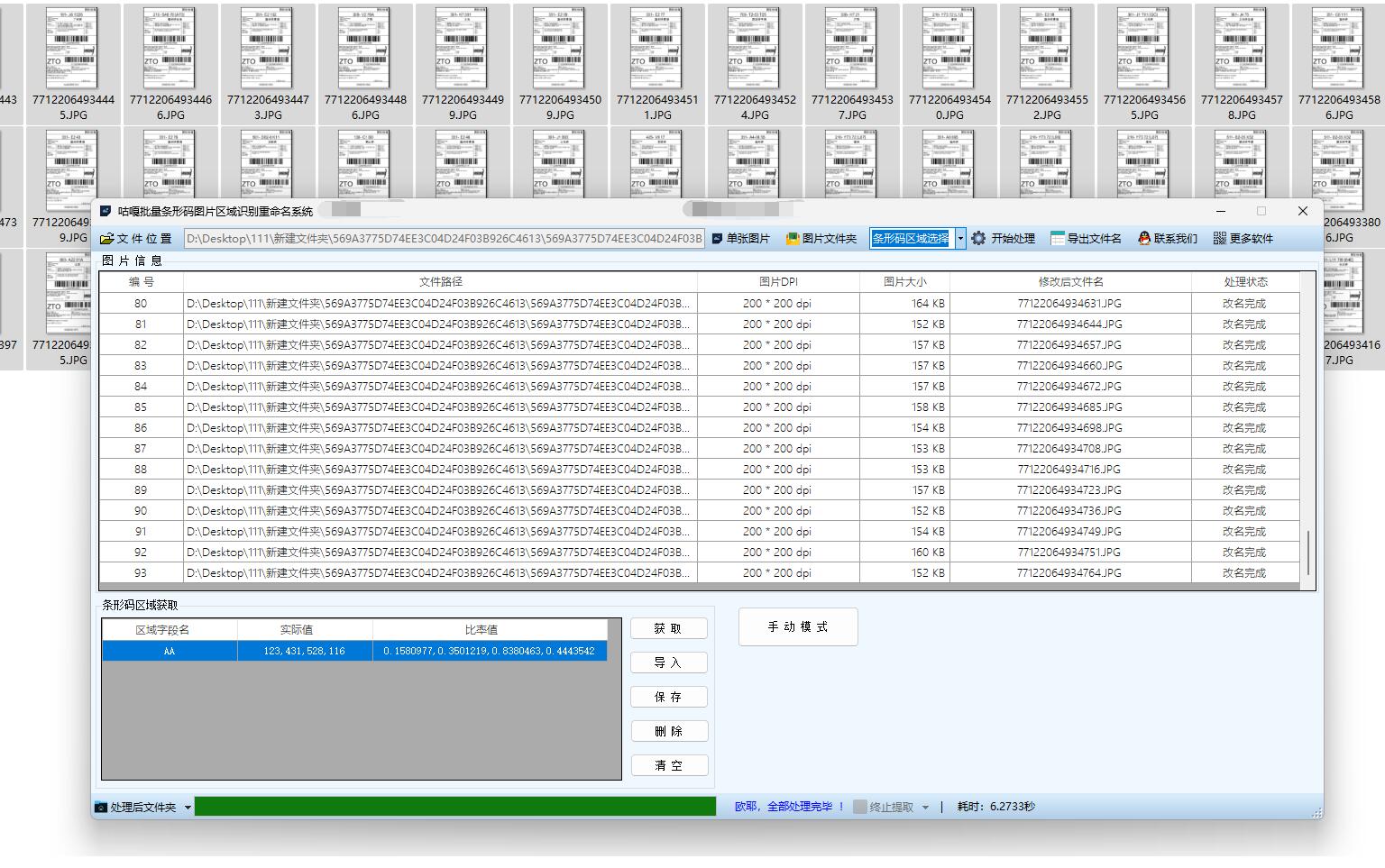
【工具教程】多个条形码识别用条码内容对图片重命名,批量PDF条形码识别后用条码内容批量改名,使用教程及注意事项
一、条形码识别改名使用教程 打开软件并选择处理模式:打开软件后,根据要处理的文件类型,选择 “图片识别模式” 或 “PDF 识别模式”。如果是处理包含条形码的 PDF 文件,就选择 “PDF 识别模式”;若是处理图片文件&…...

Python异步编程:深入理解协程的原理与实践指南
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 持续学习,不断…...

【threejs】每天一个小案例讲解:创建基本的3D场景
代码仓 GitHub - TiffanyHoo/three_practices: Learning three.js together! 可自行clone,无需安装依赖,直接liver-server运行/直接打开chapter01中的html文件 运行效果图 知识要点 核心三要素 场景(Scene) 使用 THREE.Scene(…...

FTPS、HTTPS、SMTPS以及WebSockets over TLS的概念及其应用场景
一、什么是FTPS? FTPS,英文全称File Transfer Protocol with support for Transport Layer Security (SSL/TLS),安全文件传输协议,是一种对常用的文件传输协议(FTP)添加传输层安全(TLS)和安全套接层(SSL)加密协议支持的扩展协议。…...

Java在word中指定位置插入图片。
Java使用(Poi-tl) 在word(docx)中指定位置插入图片 Poi-tl 简介Maven 依赖配置Poi-tl 实现原理与步骤1. 模板标签规范2.完整实现代码3.效果展示 Poi-tl 简介 Poi-tl 是基于 Apache POI 的 Java 开源文档处理库,专注于…...
