算法修炼之路之二分查找
目录
一:三大二分介绍及模板
1.普通二分
2.查找左右边界的二分及模板
二:LeetCode OJ练习
1.第一题
2.第二题
3.第三题
4.第四题
5.第五题
6.第六题
一:三大二分介绍及模板
1.普通二分
这里通过一道题来引出普通二分及模板
LeetCode_704 二分查找
画图分析:

具体代码:
int search(vector<int>& nums, int target) {int left=0,right=nums.size()-1;while(left<=right){int mid=left+(right-left)/2;if(nums[mid]>target) right=mid-1;else if(nums[mid]<target) left=mid+1;else return mid;}return -1;}普通二分模板

2.查找左右边界的二分及模板
通过题来引出
LeetCode_34 在排序数组中查找元素的第一个和最后一个位置
画图分析:

具体代码:
vector<int> searchRange(vector<int>& nums, int target) {//处理边界情况if(nums.size()==0) return {-1,-1};int left=0,right=nums.size()-1;int begin=0;//查找左端点while(left<right){int mid=left+(right-left)/2;if(nums[mid]<target) left=mid+1;else right=mid;}//判断是否有结果if(nums[left]==target) begin=left;//标记一下左端点else return {-1,-1};//查找右端点left=0,right=nums.size()-1;while(left<right){int mid=left+(right-left+1)/2;if(nums[mid]>target) right=mid-1;else left=mid;}return {begin,left};}左右边界的二分模板:

二:LeetCode OJ练习
1.第一题
LeetCode_69 x的平方根
画图分析:

具体代码:
int mySqrt(int x) {//处理边界情况if(x<1) return 0;int left=1,right=x;//防止当x=INT_MAX时,right-0+1操作直接越界的while(left<right){long long mid=left+(right-left+1)/2;//防止越界if(mid*mid>x) right=mid-1;else left=mid;}return left;}2.第二题
LeetCode_35 搜索插入位置
画图分析:

具体代码:
int searchInsert(vector<int>& nums, int target) {int left=0,right=nums.size()-1;while(left<right){int mid=left+(right-left)/2;if(nums[mid]<target) left=mid+1;else right=mid;}//处理在数组末尾插入的情况if(nums[left]<target) return left+1;else return left;}3.第三题
LeetCode_852 山脉数组的峰顶索引
画图分析:

具体代码:
int peakIndexInMountainArray(vector<int>& arr) {int left=1,right=arr.size()-2;//首尾不可能是结果while(left<right){int mid=left+(right-left+1)/2;if(arr[mid]>arr[mid-1]) left=mid;else right=mid-1;}return left;}4.第四题
LeetCode_162 寻找峰值
画图分析:

具体代码:
int findPeakElement(vector<int>& nums) {int left=0,right=nums.size()-1;while(left<right){int mid=left+(right-left)/2;if(nums[mid]>nums[mid+1]) right=mid;else left=mid+1;}return left;}5.第五题
LeetCode_153 寻找旋转排序数组中的最小值
画图分析:

具体代码:
int findMin(vector<int>& nums) {int left=0,right=nums.size()-1;int t=nums[right];while(left<right){int mid=left+(right-left)/2;if(nums[mid]>t) left=mid+1;else right=mid;}return nums[left];}6.第六题
LeetCode_LCR 173 点名
画图分析:

具体代码:
int takeAttendance(vector<int>& records) {int left=0,right=records.size()-1;while(left<right){int mid=left+(right-left)/2;if(records[mid]==mid) left=mid+1;else right=mid;}//处理细节问题return records[left]==left? left+1:left;}相关文章:

算法修炼之路之二分查找
目录 一:三大二分介绍及模板 1.普通二分 2.查找左右边界的二分及模板 二:LeetCode OJ练习 1.第一题 2.第二题 3.第三题 4.第四题 5.第五题 6.第六题 一:三大二分介绍及模板 1.普通二分 这里通过一道题来引出普通二分及模板 LeetCode_704 二分查找 画图分析: 具体代…...

OpenAI预计明年将推出“代理”系统
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...

每日OJ题_牛客_重排字符串_贪心_C++_Java
目录 牛客_重排字符串_贪心 题目解析 C代码 Java代码 牛客_重排字符串_贪心 重排字符串 (nowcoder.com) 描述: 小红拿到了一个只由小写字母组成的字符串。她准备把这个字符串重排(只改变字母的顺序,不改变数量) …...

Python 进阶部分详细整理
1. 面向对象编程(OOP) 面向对象编程 (OOP) 是一种通过将程序中的数据和功能封装为对象的编程范式。OOP 基于四个核心概念:类与对象、继承、封装与多态。 类与对象 类(Class):类是创建对象的蓝图或模板。它…...

[ RK3566-Android11 ] 关于移植 RK628F 驱动以及后HDMI-IN图像延迟/无声等问题
问题描述 由前一篇文章https://blog.csdn.net/jay547063443/article/details/142059700?fromshareblogdetail&sharetypeblogdetail&sharerId142059700&sharereferPC&sharesourcejay547063443&sharefromfrom_link,移植HDMI-IN部分驱动后出现&a…...

【黑马点评】 使用RabbitMQ实现消息队列——2.使用RabbitMQ监听秒杀下单
2 使用RabbitMQ实现消息队列 2.1 修改\hm-dianping\pom.xmlpom.xml文件 添加RabbitMQ的环境 <!-- RabbitMQ--> <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-amqp</artifactId> </depe…...
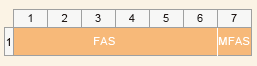
业务封装与映射 -- OTUk/ODUk/OPUk开销帧结构
开销是为了保证净荷正常、灵活传送所必须附加的供网络运行、管理和维护(OAM)使用的字节。 OTN电层开销包括OTUk开销、ODUk开销、OPUk开销、OTUCn开销、ODUCn开销、OPUCn开销和帧对齐开销。 SM开销属于OTU开销,占用3个字节;PM开销…...

Vim基本用法
Vim用法 一、基本模式 1. 普通模式(Normal Mode) 移动光标 基本移动:使用方向键(h左移、j下移、k上移、l右移),也可以使用 H(移到屏幕顶部)、M(移到屏幕中间ÿ…...

python 实现Tarjan 用于在有向图中查找强连通分量的算法
Tarjan 用于在有向图中查找强连通分量的算法介绍 Tarjan算法是一种用于在有向图中查找强连通分量的高效算法,由Robert Tarjan在1972年提出。强连通分量是指在有向图中,如果从顶点u到顶点v以及从顶点v到顶点u都存在一条路径,那么顶点u和顶点v…...
字符串去除空格,跨网段搜索不生效,设置图片显示失败问题,表格视图的批量删除,主动判断字串编码,开启向前查询的属性,画家类载入html来绘制)
Qt开发技巧(十五)字符串去除空格,跨网段搜索不生效,设置图片显示失败问题,表格视图的批量删除,主动判断字串编码,开启向前查询的属性,画家类载入html来绘制
继续讲一些Qt开发中的技巧操作: 1.字符串去除空格 我们经常会遇到字符串重去除空格的情况,对于QString去除空格,有多种场景,可能需要去除左侧、右侧、所有等位置的空格; //字符串去空格 -1移除左侧空格 0移除所有空格…...

【机器学习】智驭未来:探索机器学习在食品生产中的革新之路
📝个人主页🌹:Eternity._ 🌹🌹期待您的关注 🌹🌹 ❀目录 🔍1. 引言:探索机器学习在食品生产中的革新之路📒2. 机器学习在食品质量控制中的应用🌞实…...

Ubuntu 安装CUDA并使用Docker配置Pytorch环境
文章目录 参考安装顺序Nvidia GPU driverDockerNvidia Container ToolkitDocker PyTorch 1. Nvidia GPU Driver2. Docker 安装(使用apt存储库进行安装)3. Nvidia Container Toolkit3.1 Docker测试GPU 参考 安装顺序 Nvidia GPU driver Docker Nvidia…...

【论文阅读】Simulating 500 million years of evolution with a language model
Simulating 500 million years of evolution with a language model 1、概述 展示了语言模型在蛋白质设计和进化模拟方面的能力。通过对 ESM3 模型的研究,发现其能够生成与自然蛋白质差异较大且具有功能的新蛋白质,如新型绿色荧光蛋白(GFP),表明语言模型可以达到自然进化…...

detectron2/layers源码笔记
from .wrappers import ( BatchNorm2d, Conv2d, #在torch.conv2d的基础上集成了norm层和activation层 ConvTranspose2d, cat, interpolate, Linear, nonzero_tuple, #nonzero_tuple(x)得到tuple of 每个维度的索引 cross_entropy, empty_input_loss_func…...
LLM+知识图谱新工具! iText2KG:使用大型语言模型构建增量知识图谱
iText2KG是一个基于大型语言模型的增量知识图谱构建工具,通过从文本文档中提取实体和关系来逐步构建知识图谱。该工具具有零样本学习能力,能够在无需特定训练的情况下,在多个领域中进行知识提取。它包括文档提炼、实体提取和关系提取模块&…...

React基础-快速梳理
React介绍 React由Meta公司开发,是一个用于构建Web和原生交互界面的库 React的优势 相较于传统基于DOM开发的优势 组件化的开发方式不错的性能 相较于其它前端框架的优势 丰富的生态跨平台支持 开发环境创建 create-react-app是一个快速创建React开发环境的…...

H.264编解码 - NALU详解
一、概述 NALU(Network Abstraction Layer Unit)是H.264编解码中的一个重要概念。H.264是一种视频压缩标准,将视频数据分割成一系列的NALU。每个NALU都是一个独立的数据单元,包含视频压缩后的一个片段。每个NALU都有自己的起始码和长度前缀,用于标识NALU的起始位置和长度。…...

vSAN02:容错、存储策略、文件服务、快照与备份、iSCSI
目录 vSAN容错条带化存储策略1. 创建新策略2. 应用存储策略 vSAN文件服务文件服务快照与备份 vSAN iSCSI目标服务 vSAN容错 FTT:Fault to Tolerance 允许故障数 故障域:每一台vSAN主机是一个故障域 - 假设3台超融合(3计算1存储)&…...
:协变、逆变)
图解C#高级教程(四):协变、逆变
本章的主题是可变性(variance),这里的可变性更多的是指基类和派生类之间的转换。可变性分为三种:协变(covariance)、逆变(contravariance)和不变(invariance)…...

详解CSS中的伪元素
4.3 伪元素 可以把样式应用到文档树中根本不存在的元素上。 ::first-line 文本中的第一行 ::first-letter 文本中的第一个字母 ::after 元素之后添加 ::before 元素之前 代码: <!DOCTYPE html> <html> <head><meta charset"utf-8&q…...

STM32F4基本定时器使用和原理详解
STM32F4基本定时器使用和原理详解 前言如何确定定时器挂载在哪条时钟线上配置及使用方法参数配置PrescalerCounter ModeCounter Periodauto-reload preloadTrigger Event Selection 中断配置生成的代码及使用方法初始化代码基本定时器触发DCA或者ADC的代码讲解中断代码定时启动…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...
