基于猎豹优化算法(The Cheetah Optimizer,CO)的多无人机协同三维路径规划(提供MATLAB代码)
一、猎豹优化算法
猎豹优化算法(The Cheetah Optimizer,CO)由MohammadAminAkbari等人于2022年提出,该算法性能高效,思路新颖。
参考文献: Akbari, M.A., Zare, M., Azizipanah-abarghooee, R. et al. The cheetah optimizer: a nature-inspired metaheuristic algorithm for large-scale optimization problems. Sci Rep 12, 10953 (2022). https://doi.org/10.1038/s41598-022-14338-z

CO算法描述:

二、无人机(UAV)三维路径规划
单个无人机三维路径规划数学模型参考如下文献:
Phung M D , Ha Q P . Safety-enhanced UAV Path Planning with Spherical Vector-based Particle Swarm Optimization[J]. arXiv e-prints, 2021.
每个无人机的目标函数由路径长度成本,安全性与可行性成本、飞行高度成本和路径平滑成本共同组成:
2.1路径长度成本
路径长度成本由相邻两个节点之间的欧氏距离和构成,其计算公式如下:

2.2路径安全性与可行性成本

路径安全性与可行性成本通过下式计算:

2.3路径飞行高度成本

飞行高度成本通过如下公式计算所得:


2.4路径平滑成本

投影向量通过如下公式计算:

转弯角度的计算公式为:

爬坡角度的计算公式为:

平滑成本的计算公式为:

2.5总成本(目标函数)

总成本由最优路径成本,安全性与可行性成本、飞行高度成本和路径平滑成本的线性加权所得。其中,b为加权系数。
三、实验结果
在三维无人机路径规划中,无人机的路径由起点,终点以及起始点间的点共同连接而成。因此,自变量为无人机起始点间的各点坐标,每个无人机的目标函数为总成本(公式9)。本文研究3个无人机协同路径规划,总的目标函数为3个无人机的总成本之和。
Xmin=[Xmin0,Xmin1,Xmin2];
Xmax=[Xmax0,Xmax1,Xmax2];
dim=dim0+dim1+dim2;
fobj=@(x)GetFun(x,fobj0,fobj1,fobj2);%总的目标函数
pop=50;
maxgen=1500;[fMin ,bestX,Convergence_curve]=CO(pop,maxgen,Xmin,Xmax,dim,fobj);%Trajectories,fitness_history, population_history
% save bestX bestX
BestPosition1 = SphericalToCart(bestX(1:dim/3),model);% 第一个无人机得到的路径坐标位置
BestPosition2 = SphericalToCart(bestX(1+dim/3:2*dim/3),model1);% 第二个无人机得到的路径坐标位置
BestPosition3 = SphericalToCart(bestX(1+2*dim/3:end),model2);% 第三个无人机得到的路径坐标位置gca1=figure(1);
gca2=figure(2);
gca3=figure(3);
PlotSolution(BestPosition1,model,gca1,gca2,gca3);% 画第一个无人机
PlotSolution1(BestPosition2,model1,gca1,gca2,gca3);% 画第二个无人机
PlotSolution2(BestPosition3,model2,gca1,gca2,gca3);% 画第三个无人机figure
plot(Convergence_curve,'LineWidth',2)
xlabel('Iteration');
ylabel('Best Cost');
grid on;




相关文章:

基于猎豹优化算法(The Cheetah Optimizer,CO)的多无人机协同三维路径规划(提供MATLAB代码)
一、猎豹优化算法 猎豹优化算法(The Cheetah Optimizer,CO)由MohammadAminAkbari等人于2022年提出,该算法性能高效,思路新颖。 参考文献: Akbari, M.A., Zare, M., Azizipanah-abarghooee, R. et al. The…...

Linux:进程的创建、终止和等待
一、进程创建 1.1 fork函数初识 #include pid_t fork(void); 返回值:子进程中返回0,父进程返回子进程id,出错返回-1 调用fork函数后,内核做了下面的工作: 1、创建了一个子进程的PCB结构体、并拷贝一份相同的进程地址…...

数值优化基础——基于优化的规划算法
1 最优化问题的一般形式 最优化问题:满足一系列约束的可行域内,找到使得目标函数最小的解 min f ( x ) s.t. x...

括号匹配——(栈实现)
题目链接 有效的括号https://leetcode.cn/problems/valid-parentheses/description/ 题目要求 样例 解题代码 import java.util.*; class Solution {public boolean isValid(String str) {Stack<Character> stacknew Stack<>();for(int i0;i<str.length();i)…...

【Java 并发编程】初识多线程
前言 到目前为止,我们学到的都是有关 “顺序” 编程的知识,即程序中所有事物在任意时刻都只能执行一个步骤。例如:在我们的 main 方法中,都是多个操作以 “从上至下” 的顺序调用方法以至结束的。 虽然 “顺序” 编程能够解决相当…...

Linux下载安装MySQL8.4
这里写目录标题 一、准备工作查看系统环境查看系统架构卸载已安装的版本 二、下载MySQL安装包官网地址 三、安装过程上传到服务器目录解压缩,设置目录及权限配置my.cnf文件初始化数据库配置MySQL开放端口 一、准备工作 查看系统环境 确认Linux系统的版本和架构&am…...
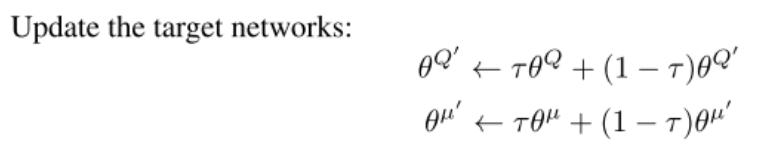
强化学习笔记之【DDPG算法】
强化学习笔记之【DDPG算法】 文章目录 强化学习笔记之【DDPG算法】前言:原论文伪代码DDPG算法DDPG 中的四个网络代码核心更新公式 前言: 本文为强化学习笔记第二篇,第一篇讲的是Q-learning和DQN 就是因为DDPG引入了Actor-Critic模型&#x…...

c++继承(下)
c继承(下) (1)继承与友元(2)继承与静态成员(3)多继承及其菱形继承问题3.1 继承模型3.2 虚继承3.3 多继承中指针偏移问题 (4)继承和组合(9…...

数据结构 ——— 单链表oj题:反转链表
目录 题目要求 手搓一个简易链表 代码实现 题目要求 给你单链表的头节点 head ,请你反转链表,并返回反转后的链表 手搓一个简易链表 代码演示: struct ListNode* n1 (struct ListNode*)malloc(sizeof(struct ListNode)); assert(n1);…...

前端项目npm install报错解决的解决办法
报错问题一: [rootspug-api spug_web]# npm install npm WARN deprecated xterm4.19.0: This package is now deprecated. Move to xterm/xterm instead. npm WARN deprecated workbox-google-analytics4.3.1: It is not compatible with newer versions of GA starting with v…...

vue双向绑定/小程序双向绑定区别
Vue双向绑定与小程序双向绑定在实现方式、语法差异以及功能特性上均存在显著区别。以下是对这两者的详细比较: 一、实现方式 Vue双向绑定 Vue的双向绑定主要通过其响应式数据系统实现。Vue使用Object.defineProperty()方法(或在Vue 3中使用Proxy对象&am…...

华为OD机试真题---字符串变换最小字符串
题目描述: 给定一个字符串s,最多只能进行一次变换,返回变换后能得到的最小字符串(按照字典序进行比较)。 变换规则: 交换字符串中任意两个不同位置的字符。 输入描述: 一串小写字母组成的字符串s 输出描述: 按照要求进行变换得到的最小字符串 补…...

JAVA基础面试题汇总(持续更新)
1、精确运算场景使用浮点型运算问题 精确运算场景(如金融领域计算应计利息)计算数字,使用浮点型,由于精度丢失问题,会导致计算后的结果和预期不一致,使用Bigdecimal类型解决此问题,示例代码如下…...

设计模式-创建型-常用:单例模式、工厂模式、建造者模式
单例模式 概念 一个类只允许创建一个对象(或实例),那这个类就是单例类,这种设计模式就叫做单例模式。对于一些类,创建和销毁比较复杂,如果每次使用都创建一个对象会很耗费性能,因此可以把它设…...

【数据结构】【链表代码】随机链表的复制
/*** Definition for a Node.* struct Node {* int val;* struct Node *next;* struct Node *random;* };*/typedef struct Node Node; struct Node* copyRandomList(struct Node* head) {if(headNULL)return NULL;//1.拷贝结点,连接到原结点的后面Node…...

Linux 系统五种帮助命令的使用
Linux 系统五种帮助命令的使用 本文将介绍 Linux 系统中常用的帮助命令,包括 man、–help、whatis、apropos 和 info 命令。这些命令对于新手和有经验的用户来说,都是查找命令信息、理解命令功能的有力工具。 文章目录 Linux 系统五种帮助命令的使用一…...

Vueron引领未来出行:2026年ADAS激光雷达解决方案上市路线图深度剖析
Vueron ADAS激光雷达解决方案路线图分析:2026年上市展望 Vueron近期发布的ADAS激光雷达解决方案路线图,标志着该公司在自动驾驶技术领域迈出了重要一步。该路线图以2026年上市为目标,彰显了Vueron对未来市场趋势的精准把握和对技术创新的坚定…...

Java | Leetcode java题解之第458题可怜的小猪
题目: 题解: class Solution {public int poorPigs(int buckets, int minutesToDie, int minutesToTest) {if (buckets 1) {return 0;}int[][] combinations new int[buckets 1][buckets 1];combinations[0][0] 1;int iterations minutesToTest /…...

怎么不改变视频大小的情况下,修改视频的时长
视频文件太大怎么变小?不影响画质的四种方法 怎么不改变视频大小的情况下,修改视频的时长 截取结尾的时间你可以使用 ffmpeg 来裁剪视频的结尾部分。假设你想去掉视频最后的3秒钟,可以先使用 ffmpeg 获取视频的总时长,然后通过指定一个新的…...

数据结构:AVL树
前言 学习了普通二叉树,发现普通二叉树作用不大,于是我们学习了搜索二叉树,给二叉树新增了搜索、排序、去重等特性, 但是,在极端情况下搜索二叉树会退化成单边树,搜索的时间复杂度达到了O(N),这…...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

Unity VR/MR开发-VR开发与传统3D开发的差异
视频讲解链接:【XR马斯维】VR/MR开发与传统3D开发的差异【UnityVR/MR开发教程--入门】_哔哩哔哩_bilibili...
