【电路基础 · 3】实际电压源 实际电流源;两种电源的等效情况;戴维南模型 诺顿模型(自用)
总览
1.实际电源的两种模型和它们的等效变换
2.两种电源的等效情况
3.戴维南模型 && 诺顿模型
一、实际电源的两种模型和它们的等效变换
1.实际电压源
实际电压源不允许短路。因为它的内阻太小,如果短路,电流很大,可能会烧毁电源。
下图中,U 是给外部电路的电压,Us 是电源的总电压。
Rs * i 则是电源自己由于内阻,分给自己的 电压。

2.实际电流源
探究实际电流源中内阻的方向:
(注意,下面这个图是不合理的。正常来说,考虑内阻之后,外部电路的电流应该减少,但是,实际却增加了)
(这是因为,我们给 Rs 的电流方向错了,流过 Rs 的电流方向应该向下)

可以看到,在伏安特性上,实际电流源 和 实际电压源呈现出对偶的关系,一个使用电阻,另一个则使用电导。

另外,实际电流源也不允许开路,因为它的内阻太大,所以分压会很大,可能会因此烧毁电源。

二、一个实际电压源和实际电流源何时完全等效
1.等效条件
对于外界电路完全相同的伏安特性。
2.如何转换
使用三角形转星型接法,或者联立它们的方程:
(设 u1 和 u2 都是 u、i1 和 i2 都是 i。这是因为它们如果等效,对外界的 u 和 i 应该是相同的)

到右下角那里是重要的公式,is = us / R1,通过这个关系,就能够推导出 G2 = 1/R1,又因为 G2 = 1/R2,所以等效的条件应该是:
R1 == R2
简略的公式变换规则:

注意,上面的变换只是让它们只是对外界电路等效,对于内部的电路是不等效的:

3.例题
例题1:
思路是这样:
我们能够将左侧的 5A 电流源 和 与它并联的 3Ω 电阻看做一个整体,也就是一个实际电流源 1。
同理,下面的 2A 电流源 和 与它并联的 4Ω 电阻看做一个整体,也就是一个实际电流源 2。
然后,根据我们之前说的 实际电压源 和 实际电流源的 互相转换公式,我们可以把它们换成两个 理想电压源!
分别为 理想电压源 1 和 理想电压源 2。它们的电压分别是(在等效条件下,电阻转换前和转换后应相等):
U1 = I1 * R1 = 5 * 3 == 15V
U2 = I2 * R2 = 2 * 4 == 8V
然后,在理想电流源转换为理想电压源之后,我们知道,电源的内阻应该从并联转为串联。
所以说,3Ω 和 4Ω 的内阻并没有改变,它们在等效替换后从并联变成了串联,总计为 7Ω。
所以等效转换后如图所示:

例题2:
思路是这样:
我们先将中间的 10V 电压源去掉(因为无论什么东西和电流源串联都可以被忽略不计)
然后,再将左侧的 10V 电压源 + 5Ω 电阻等效转化为一个 2A 电流源(I = U/R => I = 10/5 == 2)加上一个并联的 5Ω 电阻。
但是这个并联的 5Ω 电阻并没有在图中给出,图中直接化简到最后一步了。
2个 5Ω 的电阻并联,可以转化为一个 2.5Ω 的电阻。
所以最后化简后如图所示:

例题3:

思路是这样:
左侧的 6V 电压源 和 2A 电流源可以看做是并联的。因为:电压源和什么东西并联,那个东西都可以被忽略掉
所以,2A 的电流源可以被省略。
同样,我们也可以根据 电流源和什么东西串联,那个东西都可以被忽略掉,
得到,因为 6A 的电流源方向是向上的,所以,2A 的电流源可以被忽略。
此时,我们继续化简,能够将 10Ω 和 6A 的实际电流源 化简为 60V(U=IR=6 * 10==60)的电压源+1个串联的10Ω电阻。
然后,再将 60V 和 6V 串联,总的 U == 60 + 6 == 66V
加上一个 10Ω 的电阻。如下图所示:

三、戴维南模型 && 诺顿模型
1.什么是戴维南定理?
所有的电压源电流源电阻混合的电路到最后,都能够被化简为 1 个 电压源 和 1 个 电阻 => 串联的电路。

2.诺顿模型
同样的,和戴维南模型是相同的思路和原理。
只不过,诺顿模型的定义是:所有的电压源电流源电阻混合的电路到最后,都能够被化简为:
1个电流源 和 1个电阻 并联的电路。

四、其他的例题,不讲解
1.

相关文章:

【电路基础 · 3】实际电压源 实际电流源;两种电源的等效情况;戴维南模型 诺顿模型(自用)
总览 1.实际电源的两种模型和它们的等效变换 2.两种电源的等效情况 3.戴维南模型 && 诺顿模型 一、实际电源的两种模型和它们的等效变换 1.实际电压源 实际电压源不允许短路。因为它的内阻太小,如果短路,电流很大,可能会烧毁电源…...

案例-猜数字游戏
文章目录 效果展示初始画面演示视频 代码区 效果展示 初始画面 演示视频 猜数字游戏 代码区 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width,…...

POI数据的处理与分析
POI概念 POI(Point of Interest,兴趣点)数据指的是地理空间数据中的一类,表示某一具体地点或位置的信息。通常,这些数据包含位置坐标(经纬度)、名称、地址、类别和其他相关信息。POI 数据广泛应…...

ansible部分模块学习
ansible模块学习 copy模块 copy模块srcsource 源⽂件destdestination ⽬标backupbackupyes 则会在覆盖前进⾏备份mode修改权限owner修改为指定所有者group修改为指定⽤户组 案例1:传输/root/work/scripts/net-tools-install.sh⽂件到/opt/net-tools-install.sh …...

数据库(MySQL):使用命令从零开始在Navicat创建一个数据库及其数据表(二).设置主键自增等特点
前言 在上一节中,主要介绍了 Navicat Premium 17 的使用以及创建一个基础的表格。当时只设置了给数据表补充字段,没有设置给数据表删除字段。现在补充一下。 ALTER TABLE student ADD test int(4); 给名为 student 的数据表添加 test 列…...

SQL第13课——创建高级联结
本课讲另外一些联结(含义和使用方法),如何使用表别名,如何对被联结的表使用聚集函数。 13.1 使用表别名 第7课中使用别名引用被检索的表列,给列起别名的语法如下: SQL除了可以对列名和计算字段使用别名&a…...

订阅ROS2中相机的相关话题并保存RGB、深度和点云图
系统:Ubuntu22.04 ROS2版本:ROS2 humble 1.订阅ROS2中相机的相关话题并保存RGB图、深度图和点云图 ros2 topic list/stellar_1/rgb/image_raw /camera/depth/image_raw /stellar_1/points2CMakeLists.txt cmake_minimum_required(VERSION 3.15) projec…...

Open WebUI | 自托管的类 ChatGPT 网站
Open WebUI 是一个扩展性强、功能丰富且用户友好的自托管 WebUI,旨在完全离线操作。它支持各种 LLM 服务,包括 Ollama 和 OpenAI 兼容的 API。该项目在 GitHub 上已有 38k 星,非常受欢迎。 功能介绍 废话不多说,上图!…...

【Python】Python知识总结浅析
Python是一种高级编程语言,由Guido van Rossum于1991年首次发布。它以简洁的语法和强大的功能著称,适用于多种应用场景,包括Web开发、数据分析、人工智能、自动化脚本等。 易于学习和使用:Python的语法简洁明了,适合初…...

c#代码介绍23种设计模式_20策略者模式
目录 1、策略模式的定义 2、策略模式的结构 3、涉及到三个角色: 4、策略者模式在.NET中应用 5、策略者模式的适用场景 6、策略者模式的优缺点 7、实现思路 在现实生活中,策略模式的例子也非常常见,例如,中国的所得税,分为企业所得税、外商投资企业或外商企业所得税…...

FPGA-UART串口接收模块的理解
UART串口接收模块 背景 在之前就有写过关于串口模块的文章——《串口RS232的学习》。工作后很多项目都会用到串口模块,又来重新理解一下FPGA串口接收的代码思路。 关于串口相关的参数,以及在文章《串口RS232的学习》中已有详细的描述,这里就…...

复习HTML(基础)
目录 HTML含义 HTML作用 HTML的常用元素 元素的特点 元素的分类 1 是否嵌套关系 2 是否独占一行 块元素:独占一行 行内元素:共享一行 行内元素与块级元素的转换 3是否有结束标签 常用标签 1 标题标签:有六级 我们用h1 ~h6 表…...

Linux聊天集群开发之环境准备
一.windows下远程操作Linux 第一步:在Linux终端下配置openssh,输入netstate -tanp,查看ssh服务是否启动,默认端口22.。 注:如果openssh服务,则需下载。输入命令ps -e|grep ssh, 查看如否配有, ssh-agent …...

can 总线入门———can简介硬件电路
文章目录 0. 前言1. CAN简介2. 主流通讯协议对比3. CAN 硬件电路4. CAN 电平标准5. CAN 收发器 0. 前言 博客内容来自B站上CAN总线入门教程视频讲解,博客中的插图和内容均为视频中的内容。视频链接 CAN总线入门教程 1. CAN简介 先来看看一它名字的意思,…...

【重学 MySQL】六十、空间类型
【重学 MySQL】六十、空间类型 空间数据类型的分类空间数据类型的属性空间数据的表示方式空间数据的操作应用场景 在MySQL中,空间类型(Spatial Types)主要用于支持地理特征的生成、存储和分析。这些地理特征可以表示世界上具有位置的任何东西…...

python实现DES算法
DES算法 一、算法介绍1.1 背景1.2 原理1.3 基本功能函数1.3.1 初始置换函数 I P IP IP1.3.2 f f f 轮函数1.3.3 逆初始置换函数 I P − 1 IP^{-1} IP−1 1.4 子密钥的生成 二、代码实现2.1 子密钥生成实现2.2 DES加解密实现2.3 完整代码 三、演示效果 一、算法介绍 1.1 背景…...
基于LORA的一主多从监测系统_框架搭建
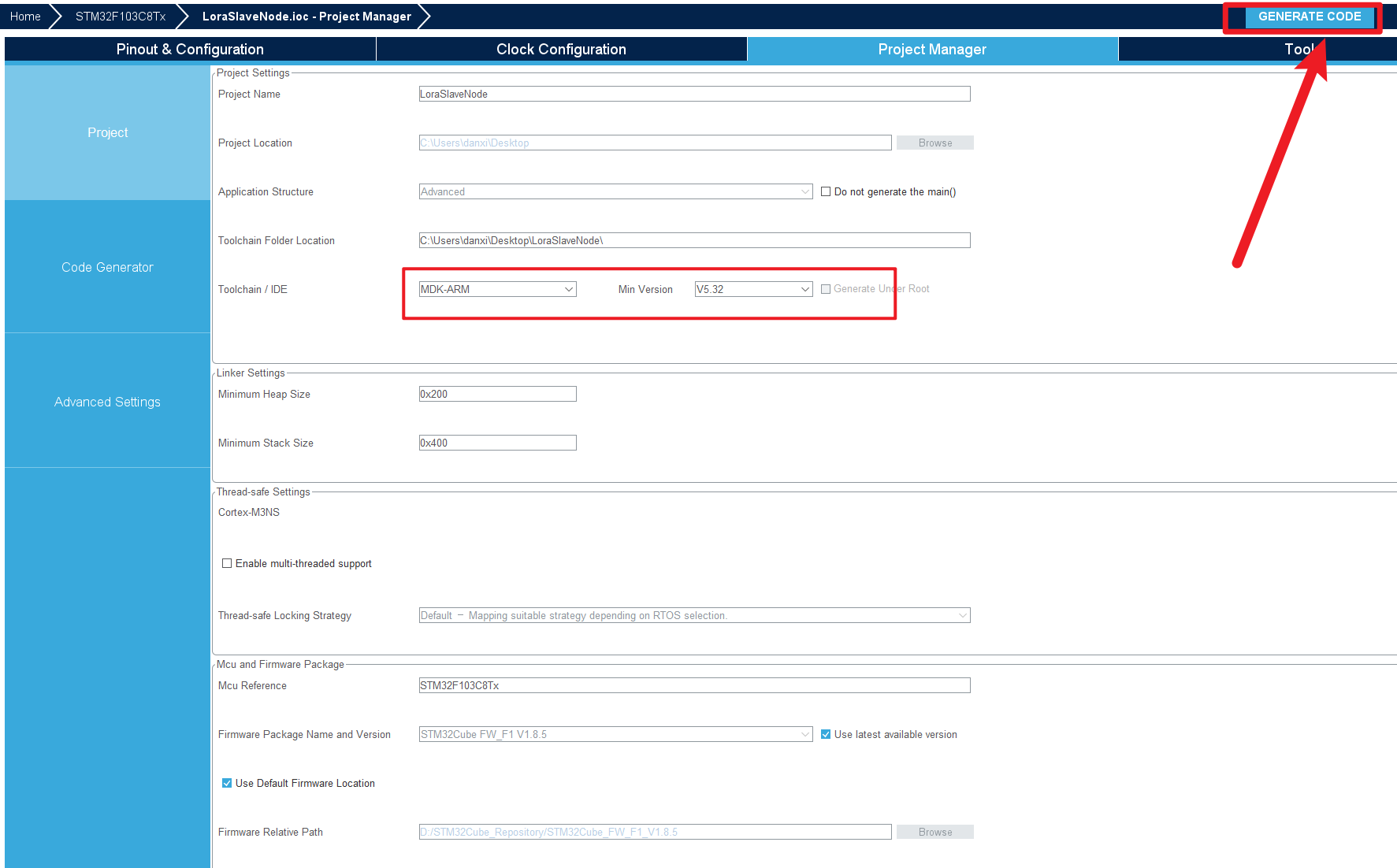
第一节、框架搭建 打开CubeMAX,选择好芯片,进行基础配置 第一步、先配置时钟源 第二步、配置SYS选项 配置debug口以及计数器源,我这里选择TIM1 第三步、选择I2C接口 配置如下即可,默认配置不用改 第四步、串口选择 我们这里使…...

优化理论及应用精解【25】
文章目录 优化学习率调度1. 阶梯衰减(Step Decay)2. 余弦退火(Cosine Annealing)3. 多项式衰减(Polynomial Decay)4. 指数衰减(Exponential Decay)总结 梯度弥散效应 参考文献 优化 …...
贝锐蒲公英网盘首发,秒建私有云,高速远程访问
虽然公共网盘带来了不少便利,但是大家对隐私泄露和重要数据泄密的担忧也随之增加。如果想要确保数据安全,自建私有云似乎是一条出路,然而面对搭建私有云的复杂步骤,许多人感到力不从心,NAS设备的成本也往往让人望而却步…...

[ 蓝桥 ·算法双周赛 ] 第 19 场 小白入门赛
🔥博客介绍: EvLast 🎥系列专栏: <<数据结构与算法>> << 算法入门>> << C项目>> 🎥 当前专栏: << 算法入门>> 专题 : 帮助小白快速入门算法竞赛 👍…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

[ICLR 2022]How Much Can CLIP Benefit Vision-and-Language Tasks?
论文网址:pdf 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用 目录 1. 心得 2. 论文逐段精读 2.1. Abstract 2…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持,不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

【WebSocket】SpringBoot项目中使用WebSocket
1. 导入坐标 如果springboot父工程没有加入websocket的起步依赖,添加它的坐标的时候需要带上版本号。 <dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-websocket</artifactId> </dep…...

2025年低延迟业务DDoS防护全攻略:高可用架构与实战方案
一、延迟敏感行业面临的DDoS攻击新挑战 2025年,金融交易、实时竞技游戏、工业物联网等低延迟业务成为DDoS攻击的首要目标。攻击呈现三大特征: AI驱动的自适应攻击:攻击流量模拟真实用户行为,差异率低至0.5%,传统规则引…...

【若依】框架项目部署笔记
参考【SpringBoot】【Vue】项目部署_no main manifest attribute, in springboot-0.0.1-sn-CSDN博客 多一个redis安装 准备工作: 压缩包下载:http://download.redis.io/releases 1. 上传压缩包,并进入压缩包所在目录,解压到目标…...
