成像基础 -- 最大对焦清晰的物距计算
最大对焦清晰的物距计算
1. 基本概念
最大对焦清晰的物距通常与景深(Depth of Field, DOF)相关,尤其是无穷远处的物体可以被清晰对焦到的距离,称为超焦距(Hyperfocal Distance)。通过计算超焦距,可以得出当镜头对焦于该距离时,从某个最小物距一直到无穷远的所有物体都可以清晰成像。
超焦距公式
超焦距的计算公式为:
H = f 2 N ⋅ c + f H = \frac{f^2}{N \cdot c} + f H=N⋅cf2+f
其中:
- H H H 是超焦距(Hyperfocal Distance)
- f f f 是镜头焦距
- N N N 是光圈数(f-number,例如 f/2.8, f/8 等)
- c c c 是弥散圆直径(Circle of Confusion, CoC),用于衡量人眼可以容忍的模糊程度,通常取决于感光元件的尺寸。
参数说明
- 焦距 f f f:镜头的焦距,单位为毫米(mm)。
- 光圈 N N N:光圈的 f 数字(如 f/2.8, f/4),数值越小光圈越大。
- 弥散圆直径 c c c:反映“清晰”的标准。对于全画幅相机,通常取 c = 0.03 mm c = 0.03 \, \text{mm} c=0.03mm。
2. 计算实例
假设我们使用一台全画幅相机(35mm 画幅),镜头焦距为 50mm,光圈为 f/8,弥散圆直径 c = 0.03 mm c = 0.03 \, \text{mm} c=0.03mm,计算超焦距。
H = 5 0 2 8 × 0.03 + 50 H = \frac{50^2}{8 \times 0.03} + 50 H=8×0.03502+50
计算步骤:
- 焦距平方: 5 0 2 = 2500 50^2 = 2500 502=2500
- 计算分母: 8 × 0.03 = 0.24 8 \times 0.03 = 0.24 8×0.03=0.24
- 计算超焦距: H = 2500 0.24 + 50 = 10416.67 + 50 = 10466.67 mm H = \frac{2500}{0.24} + 50 = 10416.67 + 50 = 10466.67 \, \text{mm} H=0.242500+50=10416.67+50=10466.67mm
因此,超焦距约为 10.47 米。
3. 最小清晰物距计算
当镜头对焦在超焦距时,从某个最小物距到无穷远都可以清晰成像。最小物距 d min d_{\text{min}} dmin 计算公式如下:
d min = H ⋅ d H + ( d − f ) d_{\text{min}} = \frac{H \cdot d}{H + (d - f)} dmin=H+(d−f)H⋅d
其中:
- d d d 是当前对焦距离
- H H H 是超焦距
- f f f 是焦距
对焦在超焦距的情况下
当镜头对焦在超焦距 H H H 时,最小清晰物距为:
d min = H 2 2 H − f d_{\text{min}} = \frac{H^2}{2H - f} dmin=2H−fH2
使用前面的例子,焦距为 50mm,超焦距为 10467mm,计算最小清晰物距:
d min = 1046 7 2 2 × 10467 − 50 ≈ 5233.5 mm = 5.23 米 d_{\text{min}} = \frac{10467^2}{2 \times 10467 - 50} \approx 5233.5 \, \text{mm} = 5.23 \, \text{米} dmin=2×10467−50104672≈5233.5mm=5.23米
因此,当对焦在超焦距时,从约 5.23 米 到无穷远的物体都会处于清晰范围内。
4. 总结
- 最大对焦清晰的物距 是通过计算超焦距来获得的,表示从某个最小距离到无穷远的物体都可以清晰成像。
- 公式 H = f 2 N ⋅ c + f H = \frac{f^2}{N \cdot c} + f H=N⋅cf2+f 用于计算超焦距,考虑了焦距、光圈大小和弥散圆等参数。
- 当镜头对焦在超焦距时,从约一半超焦距的距离到无穷远的物体都将处于清晰范围内。
相关文章:

成像基础 -- 最大对焦清晰的物距计算
最大对焦清晰的物距计算 1. 基本概念 最大对焦清晰的物距通常与景深(Depth of Field, DOF)相关,尤其是无穷远处的物体可以被清晰对焦到的距离,称为超焦距(Hyperfocal Distance)。通过计算超焦距ÿ…...

win10服务器启动且未登录时自动启动程序
场景:公司服务器安装了几个程序,当服务器断电重启之后希望程序能自动打开,而不需要手动登录服务器打开。 因为软件是自己开发的所以安全方面这里没有考虑。 1.打开服务器管理器,点击工具,选择任务计划程序 2.在任务计…...

算法专题四: 前缀和
目录 1. 前缀和2. 二维前缀和3. 寻找数组的中心下标4. 除自身以外数组的乘积5. 和为k的子数组6. 和可被K整除的子数组7. 连续数组8. 矩阵区域和 博客主页:酷酷学!!! 感谢关注~ 1. 前缀和 算法思路: 根据题意, 创建一个前缀和数组, dp[i] dp[i -1] arr[i], 再使用前缀和数组,…...

【Linux】基础IO(文件描述符、缓冲区、重定向)
🌈个人主页:秦jh__https://blog.csdn.net/qinjh_?spm1010.2135.3001.5343🔥 系列专栏:https://blog.csdn.net/qinjh_/category_12625432.html 目录 前言 C文件IO相关操作 系统文件I/O open open函数返回值 文件描述符fd re…...

一篇文章快速学会docker容器技术
目录 一、Docker简介及部署方法 1.1Docker简介 1.1.1什么是docker 1.1.2 docker在企业中的应用场景 1.1.3 docker与虚拟化的对比 1.1.4 docker的优势 二 、部署docker 2.1 容器工作方法 2.2 部署第一个容器 2.2.1 配置软件仓库 2.2.2 安装docker-ce并启动服务 2.2.…...
【MySQL】使用 JDBC 连接数据库
文章目录 前言1. 认识 JDBC1.1 概念1.2 好处 2. 使用 JDBC2.1 安装数据驱动包2.2 把 jar 包导入到项目中2.3 代码编写2.4 测试结果 3. 代码优化4. 源码展示结语 前言 在 MySQL 系列中,我们介绍了很多内容,包括但不限于建库建表,增删查改等等…...

数据结构与算法笔记:概念与leetcode练习题
1、数组Array 时间复杂度 数组访问:O(1) 数组搜索:O(N) 数组插入:O(N) 数组删除:O(N) 特点 适合读,不适合写 数组常用操作 # 1、创建数组 a [] # 2、尾部添加元素 a.append(1) a.append(2) a.append(3) # 3、…...
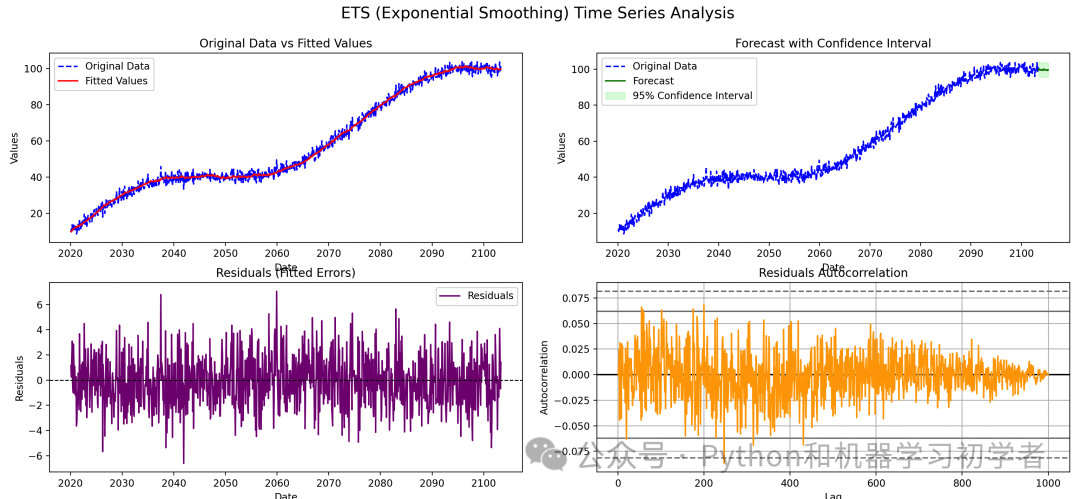
十大时间序列预测模型
目录 1. 自回归模型 原理 核心公式 推导过程: 完整案例 2. 移动平均模型 原理 核心公式 推导过程: 完整案例 3. 自回归移动平均模型 原理 核心公式 推导过程: 完整案例 4. 自回归积分移动平均模型 原理 核心公式 推导过程 完整案例 5. 季节性自回归积分…...

G2O 通过工厂函数类 OptimizationAlgorithmFactory 来生成固定搭配的优化算法
OptimizationAlgorithmFactory 类位于 optimization_algorithm_factory.h //***g2o源码 g2o/g2o/core/optimization_algorithm_factory.h ***// /*** \brief create solvers based on their short name** Factory to allocate solvers based on their short name.* The Factor…...

手机USB连接不显示内部设备,设备管理器显示“MTP”感叹号,解决方案
进入小米驱动下载界面,等小米驱动下载完成后,解压此驱动文件压缩包。 5、小米USB驱动安装方法:右击“计算机”,从弹出的右键菜单中选择“管理”项进入。 6、在打开的“计算机管理”界面中,展开“设备管理器”项&…...

SpringBootWeb快速入门!详解如何创建一个简单的SpringBoot项目?
在现代Web开发中,SpringBoot以其简化的配置和快速的开发效率而受到广大开发者的青睐。本篇文章将带领你从零开始,搭建一个基于SpringBoot的简单Web应用~ 一、前提准备 想要创建一个SpringBoot项目,需要做如下准备: idea集成开发…...

RabbitMQ 入门到精通指南
RabbitMQ 是一种开源消息代理软件,基于 AMQP(高级消息队列协议)构建,用于异步传输数据,帮助我们解耦系统、削峰流量、处理高并发。本指南将详细介绍 RabbitMQ 的架构设计、使用场景、安装步骤以及一些高级应用…...

ARM base instruction -- movz
Move wide with zero moves an optionally-shifted 16-bit immediate value to a register. 用零移动宽值将可选移位的16位即时值移动到寄存器。即把立即数移动寄存器前先把寄存器清零。 32-bit variant MOVZ <Wd>, #<imm>{, LSL #<shift>} 64-bit var…...

安装jdk安装开发环境与maven
1.下载maven 链接: https://pan.baidu.com/s/1gTmIWBFBdIQob0cqGG3E_Q 提取码: 42ck,apache-maven-3.8.4-bin.zip 2.安装java jdk yum install -y java-1.8.0-openjdk-devel 3.在/opt目录下新建目录 mkdir /opt/maven 4.将apache-maven-3.8.4-bin.zip上传到/opt/ma…...

openpnp - 图像传送方向要在高级校正之前设置好
文章目录 openpnp - 图像传送方向要在高级校正之前设置好笔记图像传送方向的确定END openpnp - 图像传送方向要在高级校正之前设置好 笔记 图像传送方向和JOG面板的移动控制和实际设备的顶部摄像头/底部摄像头要一致,这样才能和贴板子时的实际操作方向对应起来。 …...

数据库建表规范【记录】
建表规约 【强制】创建表时必须显式指定表存储引擎类型,如无特殊需求,一律为InnoDB。 【强制】必须有行数据的创建时间字段create_date和最后更新时间字段edit_date。 【强制】自增主键命名必须是id,关联表外键命名xxyyzz_id;业务…...

css的动画属性
CSS动画属性是CSS3的一个重要特性,它允许你创建平滑的过渡效果,增强用户的交互体验。CSS动画可以通过keyframes规则和animation属性来创建。 animation属性 animation属性是一个简写属性,用于设置动画的多个属性,包括动画名称、…...

【Ubuntu】PlantUML工具 | 安装 | 语法 | 使用工具画序列图
🌱 PlantUML是一个通用性很强的工具,可以快速、直接地创建各种图表。 目录 1 安装 2 使用PlantUML画序列图 ① 语法 ②示例和效果 利用简单直观的语言,用户可以毫不费力地绘制各种类型的图表。PlantUML 是一个开源项目,支持快速绘制:• 时序图• 用例图• 类图• 对...

微信步数C++
题目: 样例解释: 【样例 #1 解释】 从 (1,1) 出发将走 2 步,从 (1,2) 出发将走 4 步,从 (1,3) 出发将走 4 步。 从 (2,1) 出发将走 2 步,从 (2,2) 出发将走 3 步,从 (2,3) 出发将走 3 步。 从 (3,1) 出发将…...
AI写作工具大比拼:揭秘Claude的神秘魅力以及如何订阅Claude
AI写作困境与Claude的惊喜表现 最近有很多朋友在吐槽AI写的文章不太行,我一看他的要求写的很清楚,已经把提示词都用到位了,例如:写作背景、写作要求等,都有具体写出来。但文章阅读起来就是欠缺点啥。 你们有没有遇到…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

AI+无人机如何守护濒危物种?YOLOv8实现95%精准识别
【导读】 野生动物监测在理解和保护生态系统中发挥着至关重要的作用。然而,传统的野生动物观察方法往往耗时耗力、成本高昂且范围有限。无人机的出现为野生动物监测提供了有前景的替代方案,能够实现大范围覆盖并远程采集数据。尽管具备这些优势…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...
