在掌控板中加载人教版信息科技教学指南中的educore库
掌控板中加载educore库
人教信息科技数字资源平台(https://ebook.mypep.cn/free)中的《信息科技教学指南硬件编程代码说明》文件中提到“本程序说明主要供教学参考。需要可编程主控板须支持运行MicroPython 脚本程序。希望有更多的主控板在固件中支持educore模块”,但是教材和这个说明文件都没有指定哪种硬件。在Thonny中能安装educore库,但是导入库后出错。在https://pypi.org/project/educore/中发现此库只有
init.py里只有两行代码:
#-*- coding: utf-8 -*-
print("test")
解决方案:在https://github.com/labplus-cn/mpython/releases/tag/2.4.1中查到mpython的v2.4.1版的固件支持educore库。从https://github.com/labplus-cn/mpython/releases/download/2.4.1/mpython.bin下载mpython.bin固件。
使用mind+软件,选择上传模式,在“扩展”中选择掌控板,点击“连接设备”,找到掌控板所在的com口,在官方固件中选择“本地加载”,找到下载的mpython.bin文件,上传固件文件。

待加载成功后,点击“文件系统”下的“掌控板中的文件”即可见到上传的固件文件。

打开thonny软件(需配置解释器和端口),编写如下代码:
from educore import oled
oled.print("hello 掌控板")
运行程序,在掌控板上显示如下:

相关文章:

在掌控板中加载人教版信息科技教学指南中的educore库
掌控板中加载educore库 人教信息科技数字资源平台(https://ebook.mypep.cn/free)中的《信息科技教学指南硬件编程代码说明》文件中提到“本程序说明主要供教学参考。需要可编程主控板须支持运行MicroPython 脚本程序。希望有更多的主控板在固件中支持ed…...

关于CSS Grid布局
关于CSS Grid布局 实际效果参考 参考代码 <template><view class"baseInfo"><up-image class"cover" height"160rpx" width"120rpx" :src"bookInfo.cover"><template #error><view style"…...

初始爬虫12(反爬与反反爬)
学到这里,已经可以开始实战项目了,多去爬虫,了解熟悉反爬,然后自己总结出一套方法怎么做。 1.服务器反爬的原因 服务器反爬的原因 总结: 1.爬虫占总PV较高,浪费资源 2.资源被批量抓走,丧失竞争力…...

成像基础 -- 最大对焦清晰的物距计算
最大对焦清晰的物距计算 1. 基本概念 最大对焦清晰的物距通常与景深(Depth of Field, DOF)相关,尤其是无穷远处的物体可以被清晰对焦到的距离,称为超焦距(Hyperfocal Distance)。通过计算超焦距ÿ…...

win10服务器启动且未登录时自动启动程序
场景:公司服务器安装了几个程序,当服务器断电重启之后希望程序能自动打开,而不需要手动登录服务器打开。 因为软件是自己开发的所以安全方面这里没有考虑。 1.打开服务器管理器,点击工具,选择任务计划程序 2.在任务计…...

算法专题四: 前缀和
目录 1. 前缀和2. 二维前缀和3. 寻找数组的中心下标4. 除自身以外数组的乘积5. 和为k的子数组6. 和可被K整除的子数组7. 连续数组8. 矩阵区域和 博客主页:酷酷学!!! 感谢关注~ 1. 前缀和 算法思路: 根据题意, 创建一个前缀和数组, dp[i] dp[i -1] arr[i], 再使用前缀和数组,…...

【Linux】基础IO(文件描述符、缓冲区、重定向)
🌈个人主页:秦jh__https://blog.csdn.net/qinjh_?spm1010.2135.3001.5343🔥 系列专栏:https://blog.csdn.net/qinjh_/category_12625432.html 目录 前言 C文件IO相关操作 系统文件I/O open open函数返回值 文件描述符fd re…...

一篇文章快速学会docker容器技术
目录 一、Docker简介及部署方法 1.1Docker简介 1.1.1什么是docker 1.1.2 docker在企业中的应用场景 1.1.3 docker与虚拟化的对比 1.1.4 docker的优势 二 、部署docker 2.1 容器工作方法 2.2 部署第一个容器 2.2.1 配置软件仓库 2.2.2 安装docker-ce并启动服务 2.2.…...
【MySQL】使用 JDBC 连接数据库
文章目录 前言1. 认识 JDBC1.1 概念1.2 好处 2. 使用 JDBC2.1 安装数据驱动包2.2 把 jar 包导入到项目中2.3 代码编写2.4 测试结果 3. 代码优化4. 源码展示结语 前言 在 MySQL 系列中,我们介绍了很多内容,包括但不限于建库建表,增删查改等等…...

数据结构与算法笔记:概念与leetcode练习题
1、数组Array 时间复杂度 数组访问:O(1) 数组搜索:O(N) 数组插入:O(N) 数组删除:O(N) 特点 适合读,不适合写 数组常用操作 # 1、创建数组 a [] # 2、尾部添加元素 a.append(1) a.append(2) a.append(3) # 3、…...
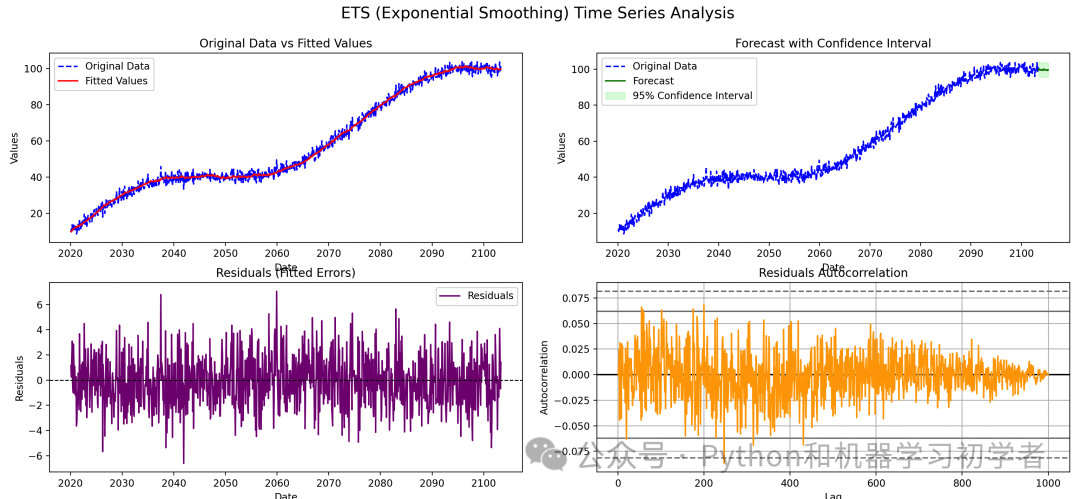
十大时间序列预测模型
目录 1. 自回归模型 原理 核心公式 推导过程: 完整案例 2. 移动平均模型 原理 核心公式 推导过程: 完整案例 3. 自回归移动平均模型 原理 核心公式 推导过程: 完整案例 4. 自回归积分移动平均模型 原理 核心公式 推导过程 完整案例 5. 季节性自回归积分…...

G2O 通过工厂函数类 OptimizationAlgorithmFactory 来生成固定搭配的优化算法
OptimizationAlgorithmFactory 类位于 optimization_algorithm_factory.h //***g2o源码 g2o/g2o/core/optimization_algorithm_factory.h ***// /*** \brief create solvers based on their short name** Factory to allocate solvers based on their short name.* The Factor…...

手机USB连接不显示内部设备,设备管理器显示“MTP”感叹号,解决方案
进入小米驱动下载界面,等小米驱动下载完成后,解压此驱动文件压缩包。 5、小米USB驱动安装方法:右击“计算机”,从弹出的右键菜单中选择“管理”项进入。 6、在打开的“计算机管理”界面中,展开“设备管理器”项&…...

SpringBootWeb快速入门!详解如何创建一个简单的SpringBoot项目?
在现代Web开发中,SpringBoot以其简化的配置和快速的开发效率而受到广大开发者的青睐。本篇文章将带领你从零开始,搭建一个基于SpringBoot的简单Web应用~ 一、前提准备 想要创建一个SpringBoot项目,需要做如下准备: idea集成开发…...

RabbitMQ 入门到精通指南
RabbitMQ 是一种开源消息代理软件,基于 AMQP(高级消息队列协议)构建,用于异步传输数据,帮助我们解耦系统、削峰流量、处理高并发。本指南将详细介绍 RabbitMQ 的架构设计、使用场景、安装步骤以及一些高级应用…...

ARM base instruction -- movz
Move wide with zero moves an optionally-shifted 16-bit immediate value to a register. 用零移动宽值将可选移位的16位即时值移动到寄存器。即把立即数移动寄存器前先把寄存器清零。 32-bit variant MOVZ <Wd>, #<imm>{, LSL #<shift>} 64-bit var…...

安装jdk安装开发环境与maven
1.下载maven 链接: https://pan.baidu.com/s/1gTmIWBFBdIQob0cqGG3E_Q 提取码: 42ck,apache-maven-3.8.4-bin.zip 2.安装java jdk yum install -y java-1.8.0-openjdk-devel 3.在/opt目录下新建目录 mkdir /opt/maven 4.将apache-maven-3.8.4-bin.zip上传到/opt/ma…...

openpnp - 图像传送方向要在高级校正之前设置好
文章目录 openpnp - 图像传送方向要在高级校正之前设置好笔记图像传送方向的确定END openpnp - 图像传送方向要在高级校正之前设置好 笔记 图像传送方向和JOG面板的移动控制和实际设备的顶部摄像头/底部摄像头要一致,这样才能和贴板子时的实际操作方向对应起来。 …...

数据库建表规范【记录】
建表规约 【强制】创建表时必须显式指定表存储引擎类型,如无特殊需求,一律为InnoDB。 【强制】必须有行数据的创建时间字段create_date和最后更新时间字段edit_date。 【强制】自增主键命名必须是id,关联表外键命名xxyyzz_id;业务…...

css的动画属性
CSS动画属性是CSS3的一个重要特性,它允许你创建平滑的过渡效果,增强用户的交互体验。CSS动画可以通过keyframes规则和animation属性来创建。 animation属性 animation属性是一个简写属性,用于设置动画的多个属性,包括动画名称、…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...

前端高频面试题2:浏览器/计算机网络
本专栏相关链接 前端高频面试题1:HTML/CSS 前端高频面试题2:浏览器/计算机网络 前端高频面试题3:JavaScript 1.什么是强缓存、协商缓存? 强缓存: 当浏览器请求资源时,首先检查本地缓存是否命中。如果命…...
