鸽笼原理与递归 - 离散数学系列(四)
目录
1. 鸽笼原理
鸽笼原理的定义
鸽笼原理的示例
鸽笼原理的应用
2. 递归的定义与应用
什么是递归?
递归的示例
递归与迭代的对比
3. 实际应用
鸽笼原理的实际应用
递归的实际应用
4. 例题与练习
例题1:鸽笼原理应用
例题2:递归计算阶乘
练习题
总结
引言
鸽笼原理和递归是离散数学中非常有趣和重要的概念。鸽笼原理(也称为抽屉原理)是一种简单却强大的逻辑工具,用于证明某些集合问题的结论,而递归则是定义和解决问题的一种非常普遍的方法,尤其是在计算机科学中有广泛应用。本篇文章将详细介绍鸽笼原理和递归的概念,并通过具体的例子和练习帮助读者深入理解这些概念。
1. 鸽笼原理
鸽笼原理的定义
鸽笼原理(Pigeonhole Principle)指出:如果有 n 个鸽子放入 m 个鸽笼,并且 n > m,那么至少有一个鸽笼里会有多个鸽子。这一原理看似简单,但在数学证明和计算机科学中有着重要的应用。
-
形式化定义:如果 n 个对象被放入 m 个容器中,且 n > m,则至少有一个容器中包含至少两个对象。
鸽笼原理的示例
-
示例1:生日悖论
-
假设有 367 个人(比一年中的天数 366 多),那么根据鸽笼原理,至少有两个人在同一天生日。这是因为一年只有 366 天,而人数超过了天数。
-
-
示例2:袜子问题
-
假设你有 10 只黑袜子和 10 只白袜子,所有袜子混合在一起。即使在黑暗中,为了确保你拿出的一定是一双同色的袜子,你需要拿出至少 3 只袜子。因为只有两种颜色,根据鸽笼原理,至少有两只袜子颜色相同。
-
鸽笼原理的应用
鸽笼原理常用于解决需要找出最小数量的集合问题。例如:
-
密码学:用于证明密码碰撞的可能性(即两个不同的输入可能映射到相同的输出)。
-
图论:用于证明某些图结构中一定存在的特性,例如在某些条件下节点之间的连接数。
2. 递归的定义与应用
什么是递归?
递归(Recursion)是指一个函数在定义自身时调用自身的现象。递归在计算机科学中非常常见,例如在数据结构、算法设计中都广泛使用。递归通常包括两个部分:
-
基准情形(Base Case):用于结束递归,防止无限递归的条件。
-
递归情形(Recursive Case):函数调用自身的部分。
-
示例:阶乘
-
阶乘函数
n!表示从 1 乘到 n,且有0! = 1。 -
递归定义为:
-
递归的示例
-
示例1:斐波那契数列
-
斐波那契数列定义为:
F(0) = 0, F(1) = 1,对于n >= 2,有F(n) = F(n-1) + F(n-2)。 -
斐波那契数列的前几项为:
0, 1, 1, 2, 3, 5, 8, 13, 21, ...
-
-
代码实现
-
用递归来实现斐波那契数列的代码如下:
-
-
示例2:归并排序
-
递归常用于排序算法,例如归并排序。归并排序通过递归将数组一分为二,分别排序,然后合并。
-
递归与迭代的对比
递归是一种自上而下的解决问题的方式,而迭代则是自下而上的。递归往往让代码更简洁,但可能带来额外的内存开销,因为每次递归调用都需要栈空间来保存上下文。
-
递归优点:代码简洁,逻辑清晰。
-
递归缺点:存在性能问题,深度递归可能导致栈溢出。
-
迭代优点:节省内存,适合处理大规模问题。
3. 实际应用
鸽笼原理的实际应用
鸽笼原理虽然简单,却在许多场景下提供了有效的证明方法。例如,在计算机网络中,鸽笼原理可以用来证明在数据包传输中,某些路由节点一定会接收到多个数据包。
递归的实际应用
递归在许多计算机科学问题中都有应用,包括:
-
树的遍历:如二叉树的深度优先遍历(DFS)。
-
图的搜索算法:如深度优先搜索。
-
动态规划:通过递归定义问题,然后通过备忘录或者表格来避免重复计算。
4. 例题与练习
例题1:鸽笼原理应用
假设有 13 个人,他们的生日都在同一个月。证明至少有两个人的生日在同一天。
解答:一个月最多有 31 天,而有 13 个人,根据鸽笼原理,至少有两个人的生日在同一天。
例题2:递归计算阶乘
编写一个递归函数来计算整数 n 的阶乘。
解答:
练习题
-
使用鸽笼原理证明:在一个有 11 人的房间里,如果每个人至少拥有一件外套,则至少有两个人拥有相同数量的外套。
-
编写一个递归函数来计算斐波那契数列的第 n 项。
总结
本文介绍了鸽笼原理和递归的基本概念。鸽笼原理是解决最小数量问题的强大工具,而递归则是一种常用的算法设计方法,广泛应用于计算机科学的各种场景中。在接下来的文章中,我们将深入探讨图论的基本概念,帮助读者理解网络结构和路径搜索等问题。希望通过这些内容,读者能更好地理解离散数学的基本原理,并学会如何应用这些方法解决实际问题。

相关文章:

鸽笼原理与递归 - 离散数学系列(四)
目录 1. 鸽笼原理 鸽笼原理的定义 鸽笼原理的示例 鸽笼原理的应用 2. 递归的定义与应用 什么是递归? 递归的示例 递归与迭代的对比 3. 实际应用 鸽笼原理的实际应用 递归的实际应用 4. 例题与练习 例题1:鸽笼原理应用 例题2:递归…...

Ubuntu 20.04常见配置(含yum源替换、桌面安装、防火墙设置、ntp配置)
Ubuntu 20.04常见配置 1. yum源配置2. 安装桌面及图形化2.1 安装图形化桌面2.1.1 选择安装gnome桌面2.1.2 选择安装xface桌面 2.2 安装VNC-Server 3. ufw防火墙策略4. 时区设置及NTP时间同步4.1 时区设置4.2 NTP安装及时间同步4.2.1 服务端(例:172.16.32…...

AI学习指南深度学习篇-生成对抗网络的基本原理
AI学习指南深度学习篇-生成对抗网络的基本原理 引言 生成对抗网络(Generative Adversarial Networks, GANs)是近年来深度学习领域的一个重要研究方向。GANs通过一种创新的对抗训练机制,能够生成高质量的样本,其应用范围广泛&…...

什么是网络安全
网络安全是指通过采取必要措施,防范对网络的攻击、侵入、干扰、破坏和非法使用以及意外事故,使网络处于稳定可靠运行的状态,以及保障网络数据的完整性、保密性、可用性的能力。 网络安全涉及多个层面,包括硬件、软件及其系统中数…...

Redis list 类型
list类型 类型介绍 列表类型 list 相当于 数组或者顺序表 list内部的编码方式更接近于 双端队列 ,支持头插 头删 尾插 尾删。 需要注意的是,Redis的下标支持负数下标。 比如数组大小为5,那么要访问下标为 -2 的值可以理解为访问 5 - 2 3 …...

Linux更改固定IP地址
1.VMware里更改虚拟网络 一: 二: 三:确定就好了 2.修改Linux系统的固定IP 一:进入此文件 效果如下: 执行以下命令: 此时IP已更改 3.远程连接 这个是前提!!! 更改网络编辑器后网络适配器可能会修改,我就是遇着这个,困住我了一会 一:可以以主机IP对应连接 连接成功 二:主机名连…...

Qt+大恒相机回调图片刷新使用方式
一、前言 上篇文章介绍了如何调用大恒SDK获得回调图片,这篇介绍如何使用这些图片并刷新到界面上。考虑到相机的帧率很高,比如200fps是很高的回调频率。那么我们的刷新频率是做不到这么快,也没必要这么快。一般刷新在60帧左右就够了。 二、思路…...

Docker 环境下 PostgreSQL 监控实战:从 Exporter 到 Prometheus 的部署详解
Docker 环境下 PostgreSQL 监控实战:从 Exporter 到 Prometheus 的部署详解 文章目录 Docker 环境下 PostgreSQL 监控实战:从 Exporter 到 Prometheus 的部署详解一 节点简述二 节点监控部署1)创建 PostgreSQL 的 exporter 账号2)…...

构建带有调试符号的srsRAN 4G
### 构建带有调试符号 首先确保已下载srsRAN 4G,并已创建并导航至构建文件夹: bash git clone https://github.com/srsran/srsran_4g.git cd srsRAN_4G mkdir build cd build 若srsRAN 4G已构建完成,应清除原有构建文件夹后继续。 可以使…...
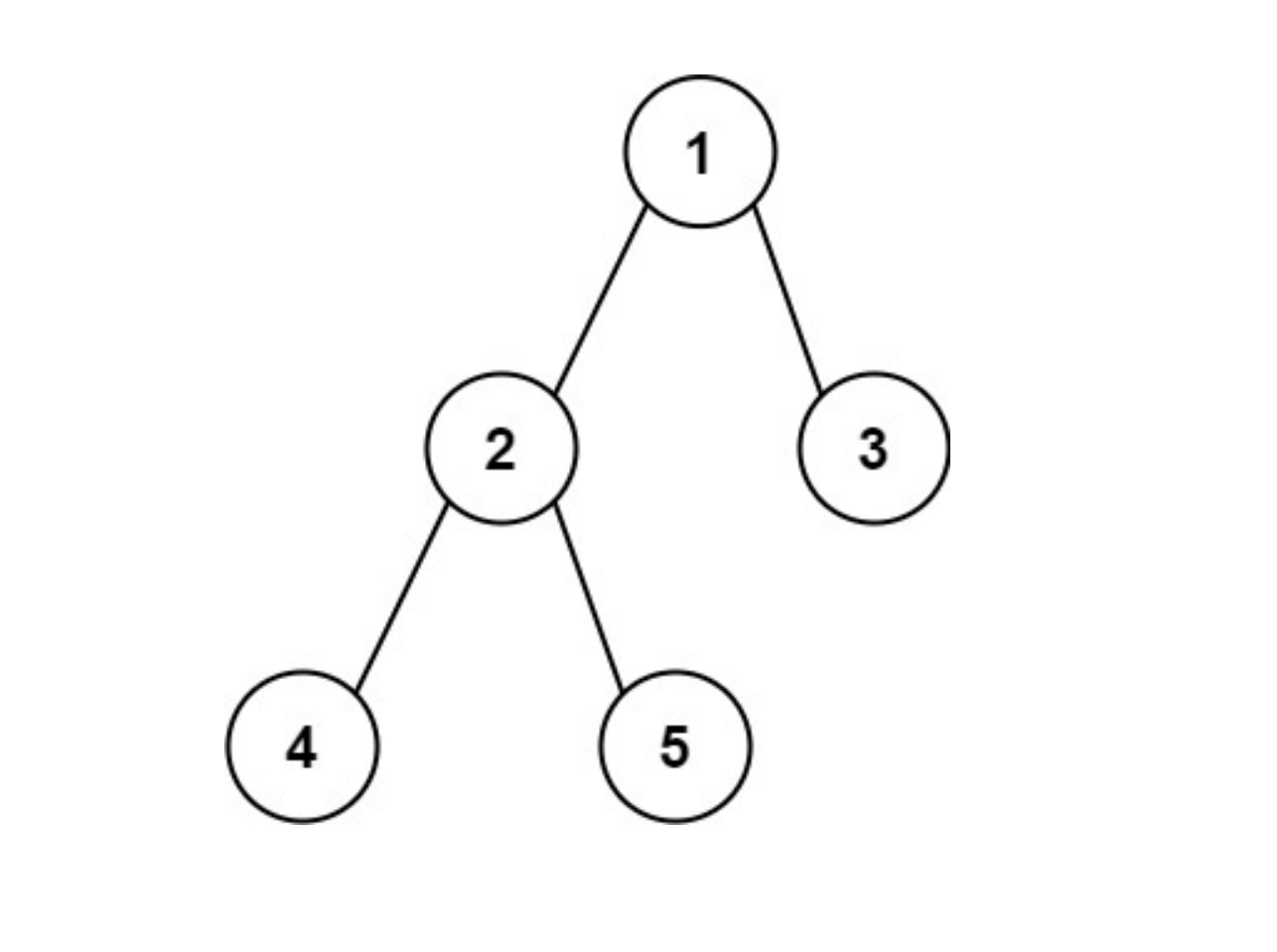
算法题总结(十)——二叉树上
#二叉树的递归遍历 // 前序遍历递归LC144_二叉树的前序遍历 class Solution {public List<Integer> preorderTraversal(TreeNode root) {List<Integer> result new ArrayList<Integer>(); //也可以把result 作为全局变量,只需要一个函数即可。…...

【MySQL】MySQL 数据库主从复制详解
目录 1. 基本概念1.1 主从架构1.2 复制类型 2. 工作原理2.1 复制过程2.2 主要组件 3. 配置步骤3.1 准备工作3.2 在主服务器上配置3.3 在从服务器上配置 4. 监控和维护4.1 监控复制状态4.2 处理复制延迟4.3 故障恢复 5. 备份策略5.1 逻辑备份与物理备份5.2 增量备份 6. 使用场景…...

一种格式化printf hex 数据的方法
格式化输出HEX数据 调试过程中通常需要个格式化输出16进制数据,为了方便美观可以参考如下方法。 #define __is_print(ch) ((unsigned int)((ch) - ) < 127u - )/*** dump_hex* * brief hex打印* * param buf: 需要打印的原始数据* param size: 原始数据类型*…...
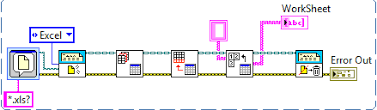
在LabVIEW中如何读取EXCEL
在LabVIEW中读取Excel文件通常使用“报告生成工具包”(Report Generation Toolkit)。以下是详细步骤: 安装工具包:确保已安装“报告生成工具包”。这通常随LabVIEW一起提供,但需要单独安装。 创建VI: 打…...

布匹瑕疵检测数据集 4类 2800张 布料缺陷 带标注 voc yolo
布匹瑕疵检测数据集 4类 2800张 布料缺陷 带标注 voc yolo 对应标注,格式VOC (XML),选配Y0L0(TXT) label| pic_ num| box_ _num hole: (425, 481) suspension_ wire: (1739, 1782) topbasi: (46, 46) dirty: (613&…...

灵动微高集成度电机MCU单片机
由于锂电技术的持续进步、消费者需求的演变、工具种类的革新以及应用领域的扩展,电动工具行业正呈现出无绳化、锂电化、大功率化、小型化、智能化和一机多能化的发展趋势。无绳化和锂电化的电动工具因其便携性和高效能的特性,已成为市场增长的重要驱动力…...

陪护小程序|护理陪护系统|陪护小程序成品
智能化,作为智慧医疗宏伟蓝图的基石,正引领着一场医疗服务的深刻变革。在这场变革的浪潮中,智慧医院小程序犹如璀璨新星,迅速崛起,而陪护小程序的诞生,更是如春风化雨,细腻地触及了老年病患、家…...

【JVM】基础篇
1 初识JVM 1.1 什么是JVM JVM 全称是 Java Virtual Machine,中文译名 Java虚拟机。JVM 本质上是一个运行在计算机上的程序,他的职责是运行Java字节码文件。 Java源代码执行流程如下: 分为三个步骤: 1、编写Java源代码文件。 …...

软件测试工程师 朝哪里进阶?
软件测试工程师 朝哪里进阶? 这里浅谈一下我的看法。 软件测试工程师 朝哪里进阶呢? 当我们测试工程师工作了2-3年后,就需要往前走往高走,就像一句名言说的:我们需要像ceo一样工作。 将自己的边界扩大一点࿰…...

Obsidian Plugin Release Pre-check
- [ ] 修改代码 - [ ] 修改README.md - [ ] 修改manifest.json - [ ] --将上述修改push到GitHub-- - [ ] 修改release版本 git tag git tag -a 1.0.6 -m "1.0.6" git push origin 1.0.6 ------------------------------------------- 备忘https://semver.org/lang/…...

Unity中实现预制体自动巡逻与攻击敌人的完整实现指南
✅作者简介:2022年博客新星 第八。热爱国学的Java后端开发者,修心和技术同步精进。 🍎个人主页:Java Fans的博客 🍊个人信条:不迁怒,不贰过。小知识,大智慧。 💞当前专栏…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

使用分级同态加密防御梯度泄漏
抽象 联邦学习 (FL) 支持跨分布式客户端进行协作模型训练,而无需共享原始数据,这使其成为在互联和自动驾驶汽车 (CAV) 等领域保护隐私的机器学习的一种很有前途的方法。然而,最近的研究表明&…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

让AI看见世界:MCP协议与服务器的工作原理
让AI看见世界:MCP协议与服务器的工作原理 MCP(Model Context Protocol)是一种创新的通信协议,旨在让大型语言模型能够安全、高效地与外部资源进行交互。在AI技术快速发展的今天,MCP正成为连接AI与现实世界的重要桥梁。…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...

文件上传漏洞防御全攻略
要全面防范文件上传漏洞,需构建多层防御体系,结合技术验证、存储隔离与权限控制: 🔒 一、基础防护层 前端校验(仅辅助) 通过JavaScript限制文件后缀名(白名单)和大小,提…...

结构化文件管理实战:实现目录自动创建与归类
手动操作容易因疲劳或疏忽导致命名错误、路径混乱等问题,进而引发后续程序异常。使用工具进行标准化操作,能有效降低出错概率。 需要快速整理大量文件的技术用户而言,这款工具提供了一种轻便高效的解决方案。程序体积仅有 156KB,…...
